↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The Procrustes-Wasserstein problem, which involves aligning high-dimensional point clouds, is a fundamental challenge in many fields like natural language processing and computer vision. Existing methods often lack theoretical guarantees, hindering their reliability and applicability to diverse datasets. Moreover, accurately measuring alignment performance is also problematic, requiring careful consideration of appropriate metrics like Euclidean transport cost.
This paper addresses these issues by introducing a planted model for the Procrustes-Wasserstein problem. Information-theoretic results are derived for both high and low-dimensional regimes, shedding light on the fundamental limits of alignment. A novel algorithm, the ‘Ping-Pong’ algorithm, is proposed, which iteratively estimates the optimal orthogonal transformation and data relabeling, improving upon the state-of-the-art approach. Sufficient conditions for the method’s success are provided, and experimental results demonstrate its superior performance compared to the existing methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between practical methods and theoretical understanding in high-dimensional data alignment. It provides novel information-theoretic results, establishing fundamental limits for the Procrustes-Wasserstein problem, and proposes a novel algorithm that outperforms current state-of-the-art methods. This work opens avenues for developing more efficient and robust alignment techniques with theoretical guarantees.
Visual Insights#
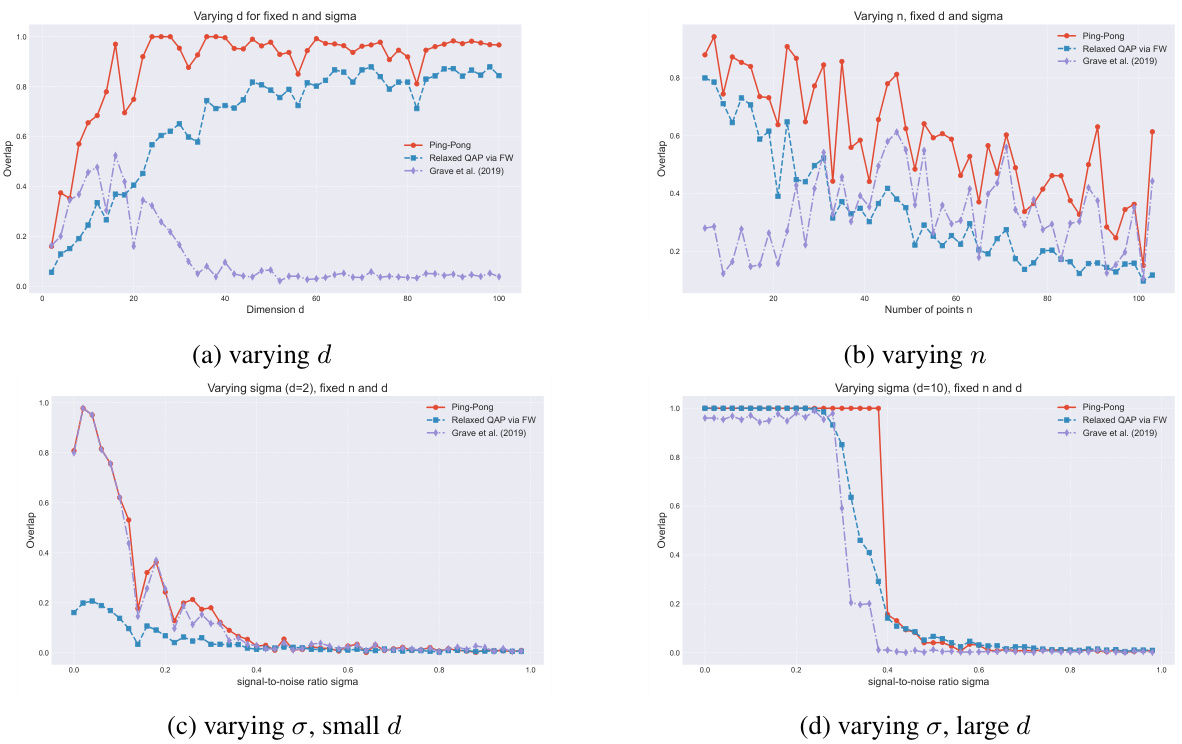
This figure compares the performance of three different algorithms for solving the Procrustes-Wasserstein problem across different parameter settings. The x-axis of each subplot varies a different parameter (dimensionality, number of points, noise level), while the y-axis shows the overlap, a measure of alignment accuracy. The three algorithms compared are: the relaxed QAP estimator, the Ping-Pong algorithm (proposed in the paper), and the algorithm from Grave et al. (2019). The plots illustrate how the accuracy of each algorithm changes depending on the dimensionality of the data, the number of points, and the level of noise present.

This table summarizes the informational results from previous research papers on the Procrustes-Wasserstein problem and compares them to the results presented in this paper. It shows the different settings (e.g., whether the orthogonal transformation is the identity matrix), the performance metrics used (overlap and transport cost), the dimensional regimes considered (high-dimensional, low-dimensional, etc.), and the conditions under which exact or approximate recovery of the permutation and orthogonal transformation is possible. The table provides a concise overview of the key findings across multiple studies, highlighting the contributions of the current paper.
Full paper#