Alleviate Anchor-Shift: Explore Blind Spots with Cross-View Reconstruction for Incomplete Multi-View Clustering

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on incomplete multi-view clustering because it introduces a novel method to effectively address the anchor-shift problem, a major limitation of existing anchor-based methods. The proposed AIMC-CVR not only enhances clustering accuracy and scalability but also opens new avenues for exploring blind spots in sample reconstruction using affine combinations. This work has the potential to significantly impact the field by providing a more robust and efficient solution to a long-standing problem.

Visual Insights

#

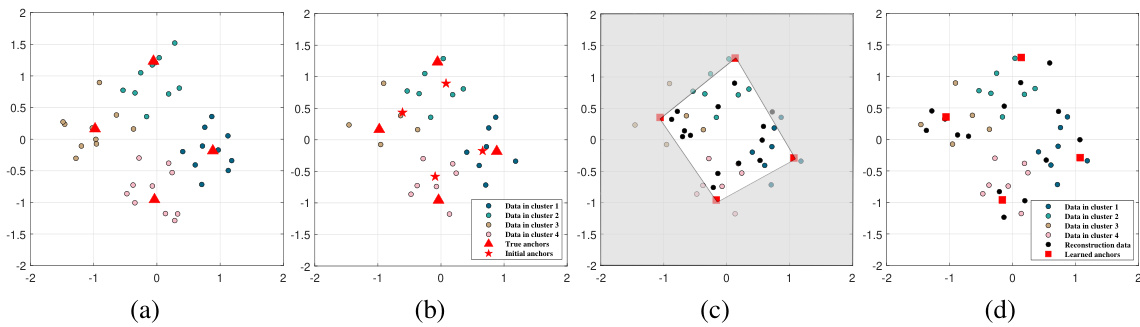
This figure shows the impact of missing data on anchor learning and data reconstruction. (a) shows anchors learned from complete data, while (b) shows anchors initialized from incomplete data, illustrating the anchor-shift problem. (c) and (d) demonstrate the difference between data reconstruction using convex combinations and affine combinations. Convex combinations restrict reconstruction to the convex hull of the anchors, while affine combinations allow for reconstruction outside this hull, illuminating ‘blind spots’ in the data.

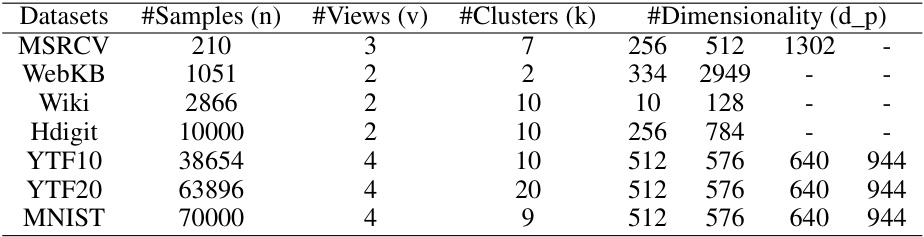
This table lists the seven datasets used in the paper’s experiments, along with their characteristics: the number of samples (n), the number of views (v), the number of clusters (k), and the dimensionality (d_p) of each view. The datasets represent a variety of data types and sizes, allowing for a comprehensive evaluation of the proposed AIMC-CVR method under diverse conditions.

In-depth insights

#

Anchor Shift Problem

#

The Anchor Shift problem, as discussed in the context of incomplete multi-view clustering, highlights a critical weakness in anchor-based methods. These methods rely on selecting a small subset of representative samples (anchors) to efficiently capture the overall data structure. However, when dealing with incomplete data (missing values across views), the learned anchors become skewed and misaligned. This is because the anchor learning process is guided by the available data, which is incomplete and potentially biased. Consequently, the anchors may not accurately represent the true underlying data distribution, leading to suboptimal clustering results. The shift in anchor positions due to missing data is the crux of the problem. This distortion affects the similarity measurements and relationships between samples and anchors, impacting the accuracy and effectiveness of downstream clustering tasks. Addressing the anchor shift necessitates techniques that robustly learn anchors from incomplete data, possibly through cross-view learning strategies or imputation methods that accurately reconstruct the missing data without introducing further bias.

Cross-View Reconstruction

#

Cross-view reconstruction, in the context of incomplete multi-view clustering, is a crucial technique to address the challenge of missing data across multiple views. It leverages the complementary information present in different views to reconstruct missing data points, thus improving the completeness and accuracy of the data representation. A key innovation is the use of affine combinations, rather than traditional convex combinations, for reconstruction. This allows the exploration of regions outside the convex hull of available data, potentially revealing valuable insights hidden in the ‘blind spots’ of incomplete datasets. The cross-view approach ensures that the reconstruction process is informed by information from all available views, leading to more robust and accurate results. The effectiveness of this approach hinges on effectively learning robust and accurate anchor points, representative of the data’s underlying structure, which can guide the reconstruction process. Mitigating issues like anchor-shift, which can arise due to incomplete data, is vital for the success of this technique. The method demonstrates the ability to handle large-scale scenarios, avoiding the computational burdens associated with traditional approaches that rely on full similarity matrices.

Affine Combination

#

The concept of “Affine Combination” in the context of the provided research paper appears to address a critical limitation of traditional convex combination methods for handling missing data in multi-view clustering. Convex combinations, used in many existing anchor-based methods, restrict the reconstruction of missing samples to the convex hull of the learned anchors, creating “blind spots.” The proposed affine combination approach transcends this limitation by allowing the reconstruction of samples outside the convex hull, effectively exploring areas previously inaccessible. This is achieved by relaxing the constraints of convex combinations, thereby enabling a more comprehensive and accurate representation of the data, including those samples with missing values. The inclusion of affine combinations significantly enhances the flexibility and expressiveness of the model, allowing for a finer-grained reconstruction and potentially leading to improved clustering results. This extension directly addresses the “anchor-shift” problem, a key challenge highlighted in the paper, demonstrating its importance in developing more robust and accurate multi-view clustering techniques.

Scalability and Efficiency

#

A crucial aspect of any machine learning model is its scalability and efficiency. Scalability refers to the model’s ability to handle increasingly large datasets and complex tasks without significant performance degradation. Efficiency focuses on minimizing computational resources (time and memory) required for training and inference. In the context of multi-view clustering, achieving both is challenging due to the inherent complexity of integrating information from multiple data sources. Anchor-based methods offer a potential solution, drastically reducing computational costs compared to methods that build full similarity matrices. However, the effectiveness of anchor-based approaches often hinges on the quality of anchor selection and the ability to effectively handle missing data. Therefore, strategies like cross-view reconstruction and affine combinations, as explored in the paper, are critical to achieving both scalability and efficiency, particularly when dealing with incomplete data which is common in real-world applications. Careful design choices, such as the optimized projection mechanisms and reconstruction strategies, are essential to mitigating the computational burden without sacrificing accuracy.

High-Dimensional Data

#

High-dimensional data presents significant challenges in various machine learning tasks, including clustering. The curse of dimensionality leads to sparsity and increased computational complexity, making traditional methods less effective. Techniques like dimensionality reduction become crucial to mitigate these issues, often involving feature selection or transformation to lower-dimensional spaces while preserving essential information. However, careful consideration is needed to avoid the loss of critical features or the introduction of unwanted biases. The choice of dimensionality reduction method significantly impacts the performance of subsequent algorithms. Anchor-based methods have been proposed to address scalability issues with large datasets, and their effectiveness in high-dimensional settings needs careful evaluation; the trade-off between computational efficiency and information preservation in high-dimensional scenarios needs to be investigated further. Another crucial aspect is the impact of noise and missing values, which become more pronounced in high-dimensional space, requiring robust preprocessing steps.

More visual insights

#

More on figures

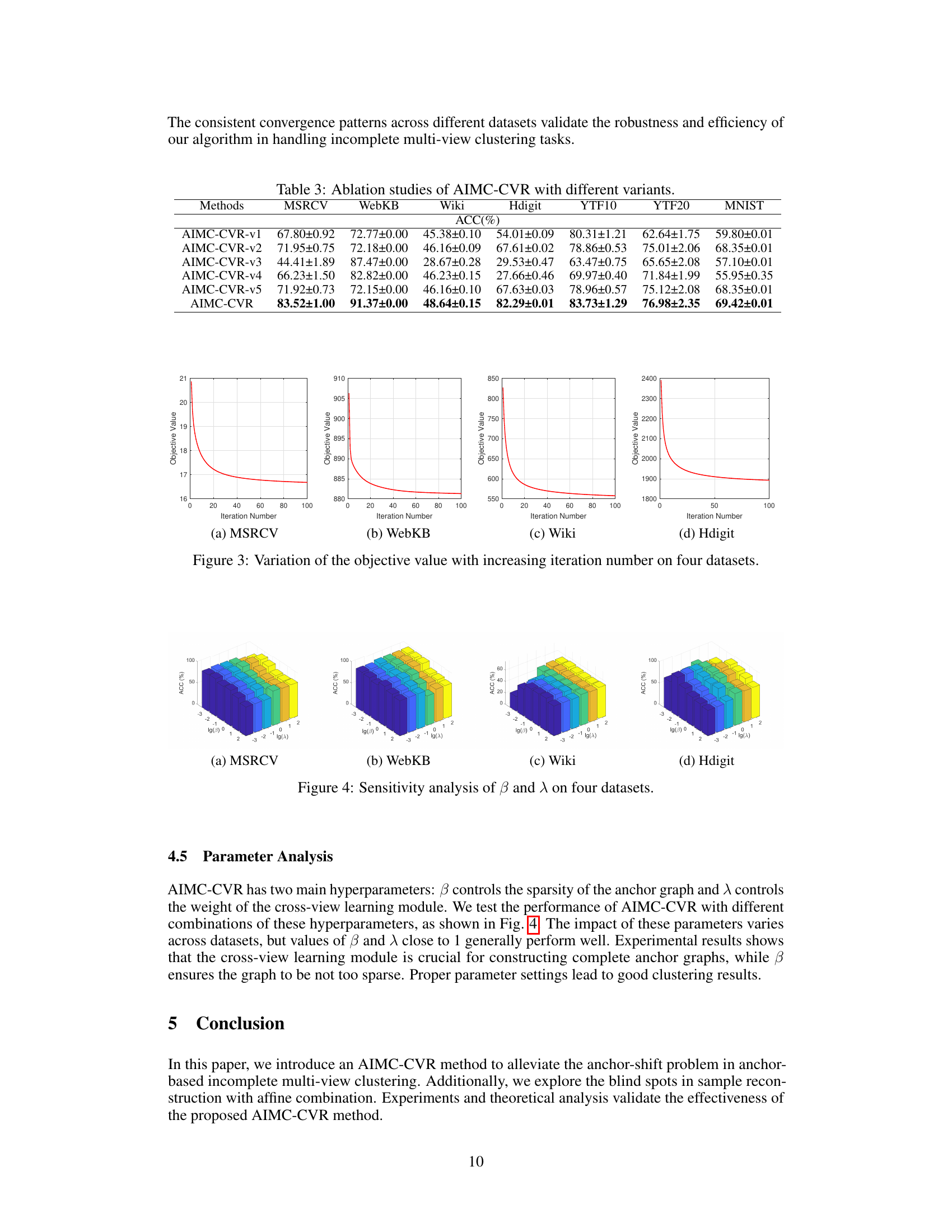
This figure displays the accuracy (ACC) of various incomplete multi-view clustering algorithms across seven datasets at different missing rates. Each line represents a different algorithm, and the x-axis represents the percentage of missing data. The y-axis shows the clustering accuracy. The figure illustrates how the performance of each algorithm changes as the amount of missing data increases. The proposed AIMC-CVR algorithm consistently outperforms the other algorithms across all datasets and missing rates.

This figure illustrates the impact of missing data on anchor learning and data reconstruction. (a) shows how anchors are learned in complete data, forming well-defined clusters. (b) shows that when data is incomplete, the initialized anchors shift away from their positions in (a). (c) demonstrates that using convex combinations for reconstruction limits the reconstructed data to the convex hull defined by the anchors, leading to blind spots. (d) shows that using affine combinations for reconstruction allows exploring areas beyond the convex hull, improving data representation and mitigating the anchor shift problem.

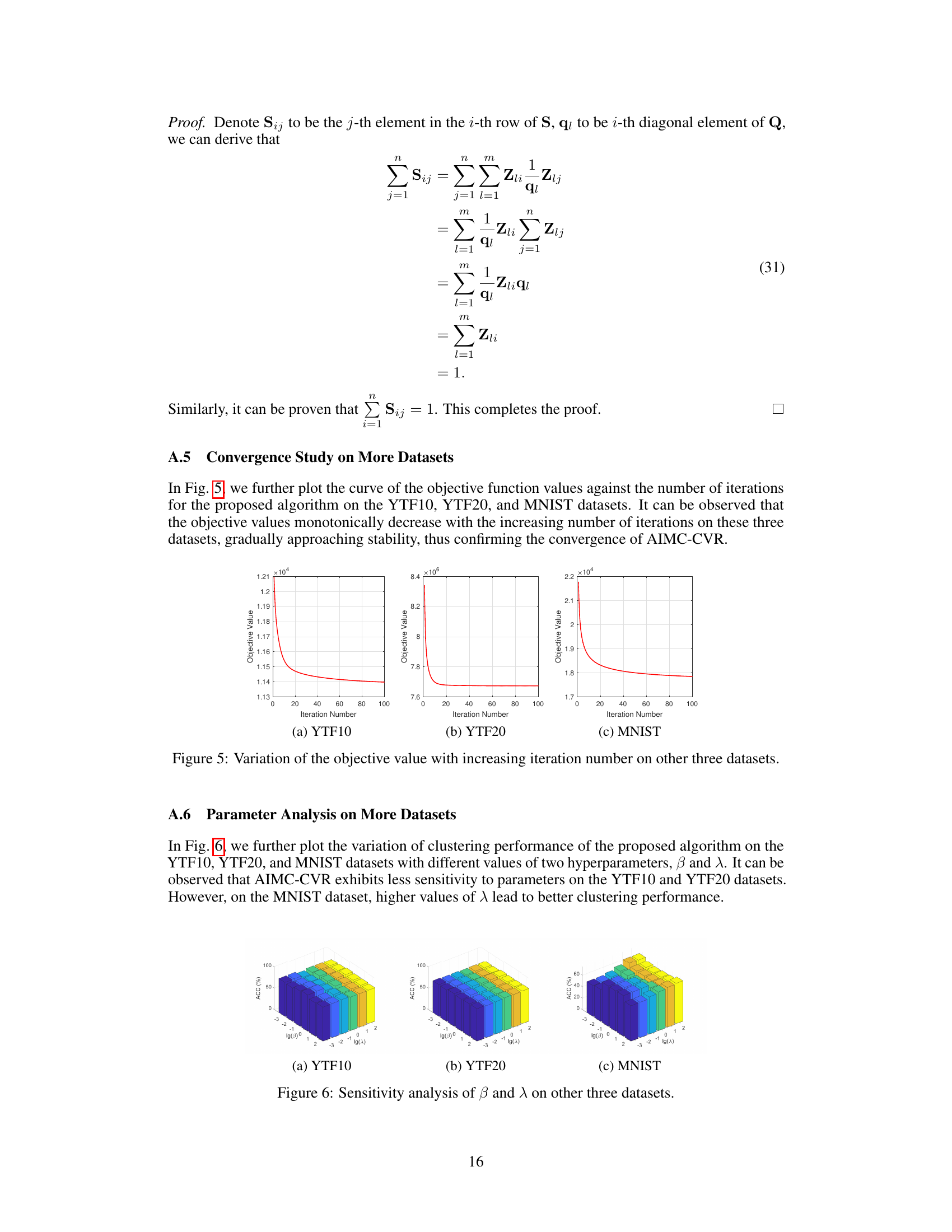
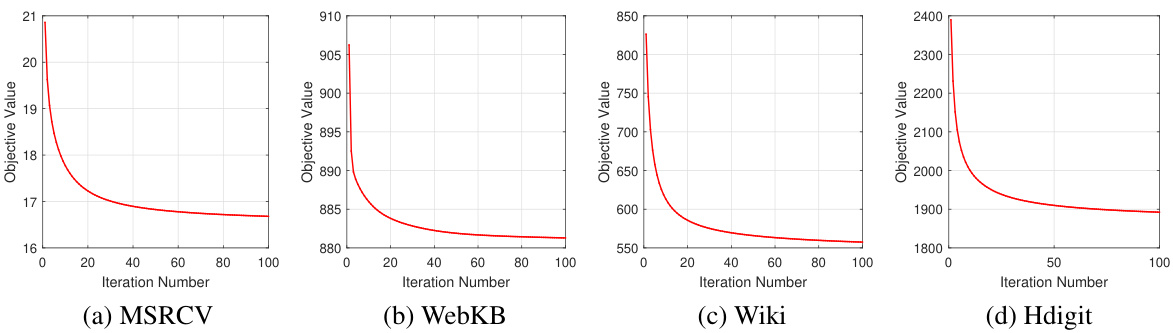
This figure presents a sensitivity analysis of the hyperparameters β and λ used in the AIMC-CVR model. Four subplots display the clustering accuracy (ACC) across four different datasets (MSRCV, WebKB, Wiki, and Hdigit) for various combinations of β and λ values. The x-axis represents log(λ), and the y-axis represents log(β). Each bar represents the ACC for a specific combination of hyperparameter values, providing insight into the model’s performance across a range of settings.

This figure illustrates the impact of missing data on anchor learning and data reconstruction. (a) shows the ideal case where anchors are learned from complete data. (b) demonstrates the anchor shift problem where anchors are learned from incomplete data, resulting in their misalignment. (c) and (d) compare the results of convex and affine combinations, respectively, during data reconstruction. Convex combination limits reconstruction to the convex hull of the anchors, leading to blind spots. Affine combination extends beyond the convex hull, illuminating these blind spots and allowing for a more accurate reconstruction of the missing data. This highlights the core advantage of the proposed method that addresses the blind spots by using affine combination-based reconstruction strategy.

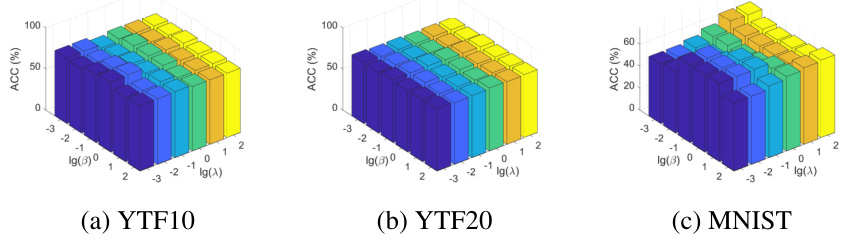
This figure shows a 3D surface plot visualizing the sensitivity analysis of the hyperparameters β (sparsity of the anchor graph) and λ (balancing the influence of the two modules) on the clustering performance (measured by ACC) for three datasets: YTF10, YTF20, and MNIST. Each plot shows how the ACC varies with different combinations of β and λ, providing insights into the optimal parameter settings for each dataset.

More on tables

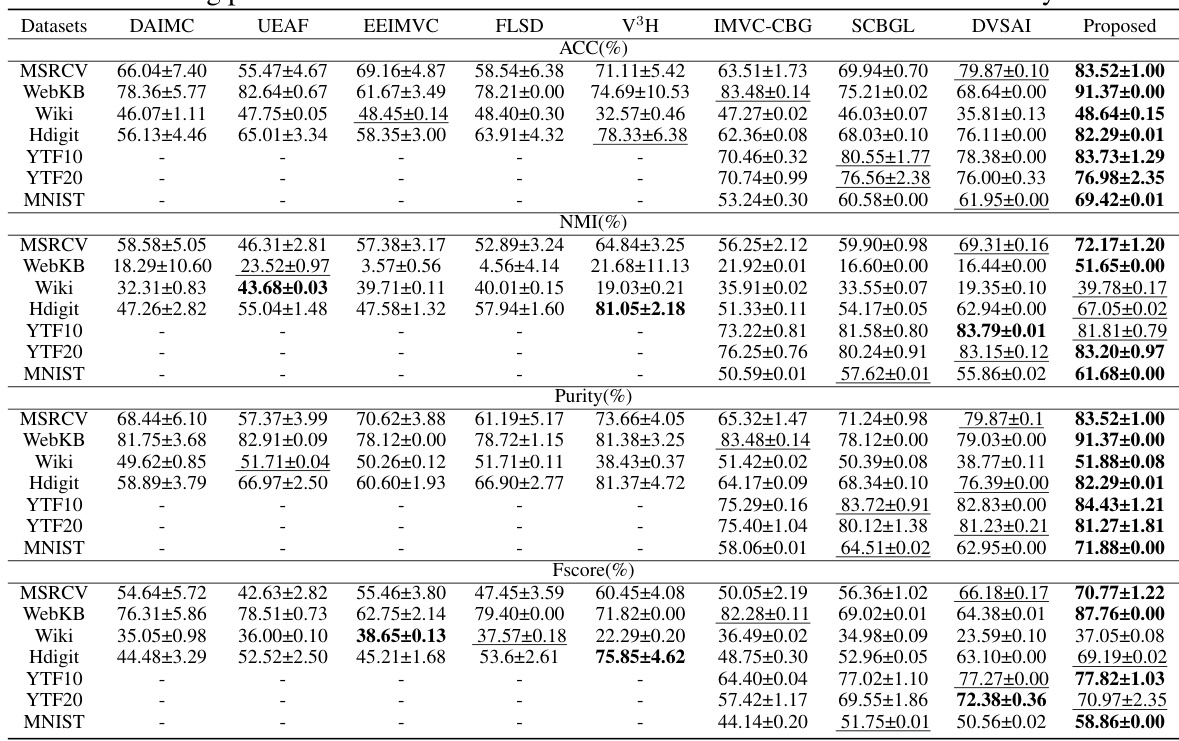
This table presents a comparison of the proposed AIMC-CVR method against eight state-of-the-art incomplete multi-view clustering algorithms across seven benchmark datasets. The performance is evaluated using four metrics: Accuracy (ACC), Normalized Mutual Information (NMI), Purity, and F-score. The table highlights the superior performance of AIMC-CVR, especially on smaller datasets, and its scalability in handling large-scale datasets where other methods fail due to memory constraints. The ‘-’ indicates that a method could not be run due to memory limitations on the given dataset.

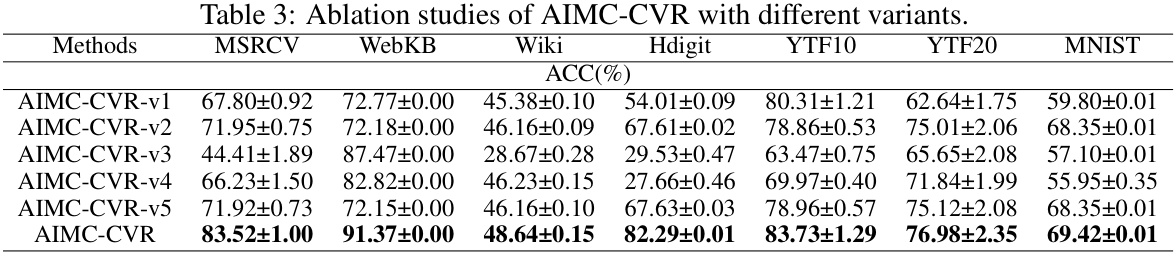
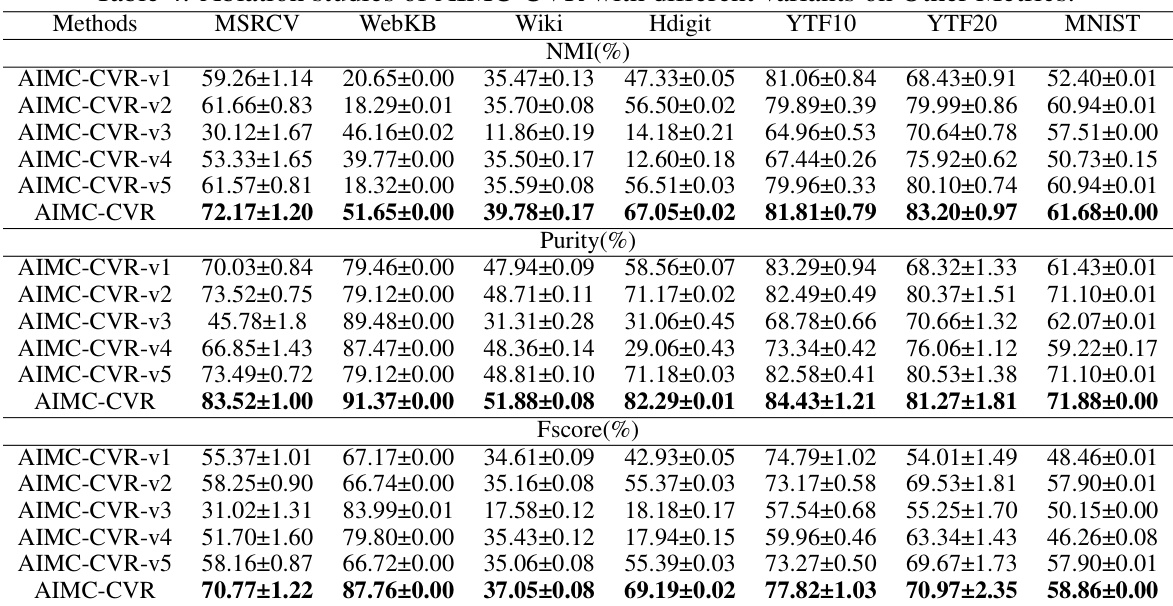
This table presents the results of an ablation study comparing the performance of the proposed AIMC-CVR method against five variants. Each variant removes or modifies a key component of AIMC-CVR, allowing for an analysis of the contribution of each part to the overall performance. The results are presented in terms of clustering accuracy (ACC) across seven different datasets (MSRCV, WebKB, Wiki, Hdigit, YTF10, YTF20, MNIST). The table demonstrates the effectiveness of each component and the superiority of the complete AIMC-CVR model.

This table presents a comparison of the clustering performance of AIMC-CVR and eight other state-of-the-art incomplete multi-view clustering algorithms across seven datasets. The performance is measured using four metrics: Accuracy (ACC), Normalized Mutual Information (NMI), Purity, and F-score. The datasets vary in size and number of views. The table highlights AIMC-CVR’s superior or competitive performance across all datasets and its ability to handle larger datasets where other methods fail due to memory limitations.

Full paper

#