↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Data assimilation, vital for accurate weather forecasting, struggles with real-world data’s varying resolutions. Existing AI methods often require pre-processing, leading to errors and limiting generalization. This necessitates a flexible approach that handles diverse resolutions efficiently.
The proposed Fourier Neural Processes (FNP) directly addresses this by using a flexible neural network architecture. It achieves state-of-the-art accuracy, particularly with high-resolution data, and shows superior generalization capabilities by handling unseen resolutions and different tasks (assimilation and reconstruction) without needing retraining. This enhances accuracy and efficiency in data assimilation.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles a critical challenge in data assimilation—handling diverse data resolutions. Its novel Fourier Neural Processes (FNP) offers a flexible and generalizable solution, improving accuracy and efficiency, especially with high-resolution datasets. This opens doors for more accurate weather forecasting and other Earth system studies. The FNP’s excellent generalization across resolutions and tasks is especially valuable.
Visual Insights#
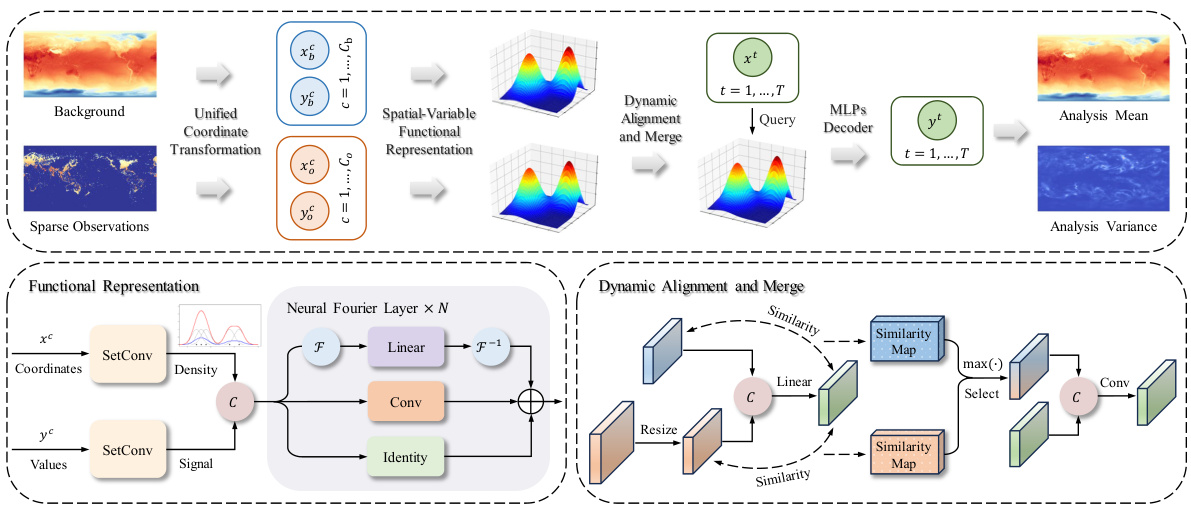
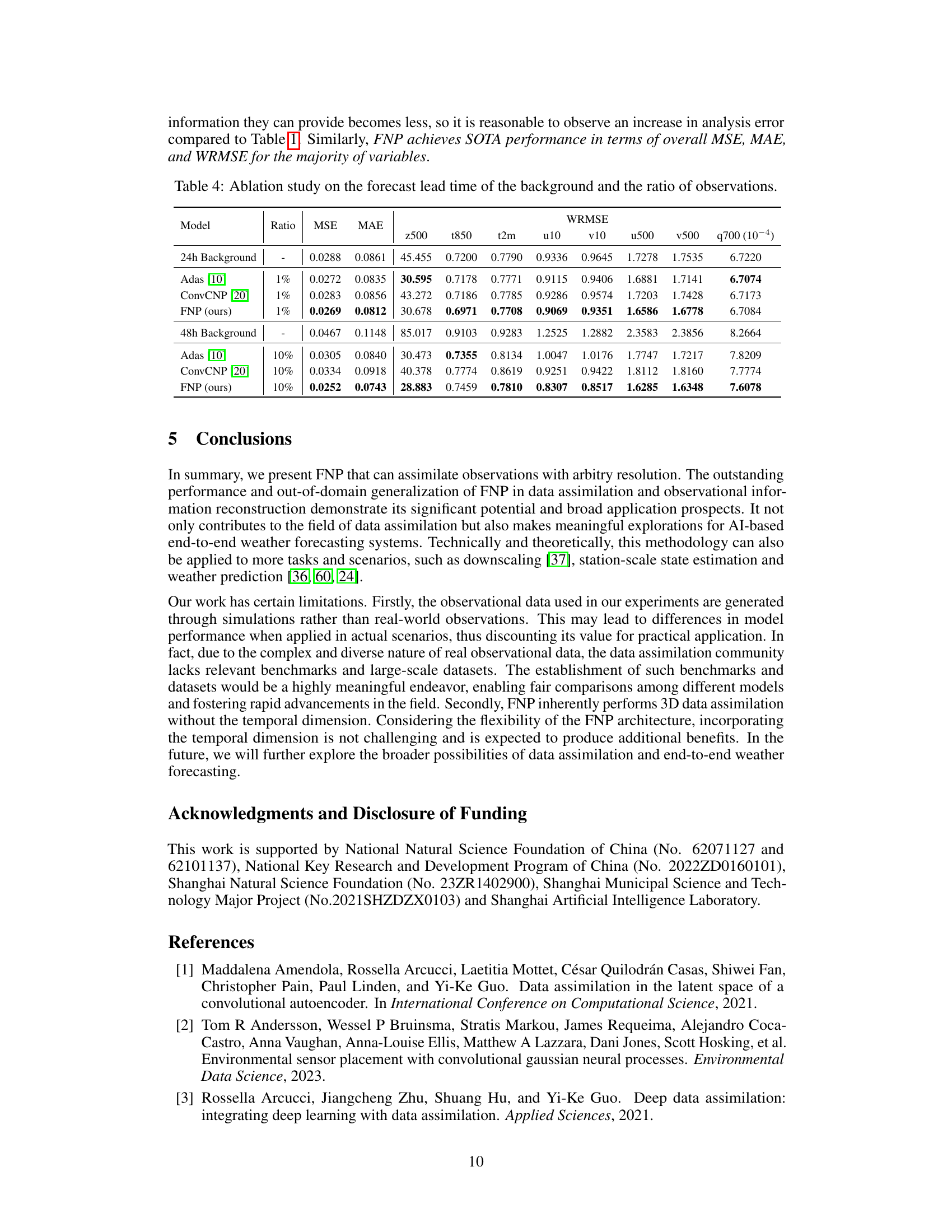
This figure provides a high-level overview of the Fourier Neural Processes (FNP) architecture. It illustrates the flow of data through different modules, starting from the input of background and sparse observation data to the final output of the analysis mean and variance. Key modules like unified coordinate transformation, spatial-variable functional representation, dynamic alignment and merge, and the decoder are highlighted. The figure also includes a detailed breakdown of the functional representation and dynamic alignment and merge modules, showing the specific operations and transformations performed within each.

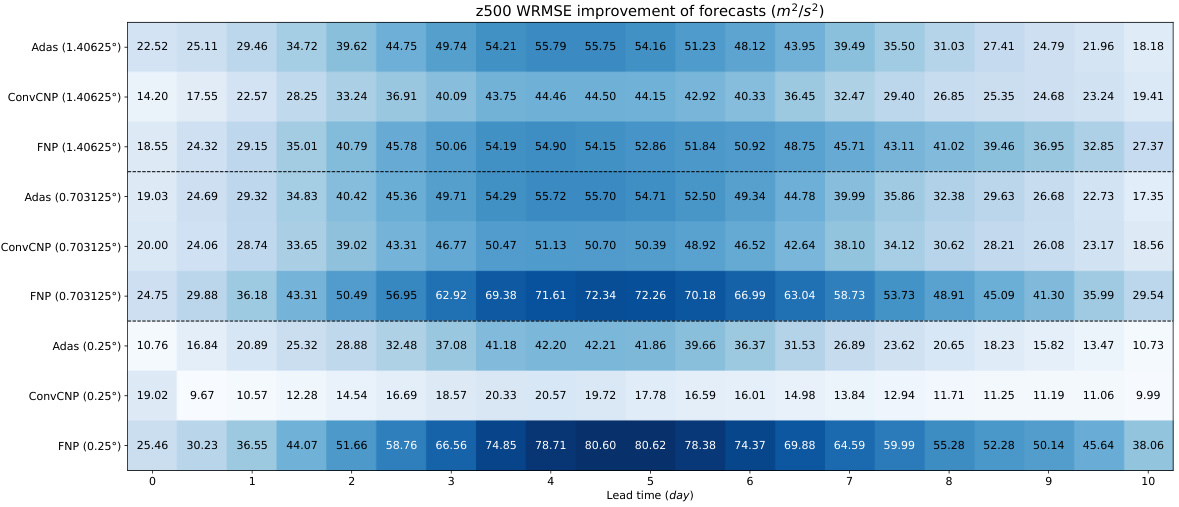
This table presents a quantitative comparison of the analysis errors for different data assimilation models at various resolutions (1.40625°, 0.703125°, and 0.25°). It shows the Mean Square Error (MSE), Mean Absolute Error (MAE), and latitude-weighted Root Mean Square Error (WRMSE) for several meteorological variables (z500, t850, t2m, u10, v10, u500, v500, and q700). The results are compared with and without fine-tuning for some models, highlighting the impact of resolution on model performance and the ability of the Fourier Neural Process (FNP) to handle arbitrary resolutions effectively.
In-depth insights#
Arbitrary-Res Assim#
The concept of ‘Arbitrary-Res Assim,’ likely referring to arbitrary-resolution data assimilation, presents a significant advancement in data assimilation techniques. Traditional methods often struggle with data of varying resolutions, requiring pre-processing steps that can introduce errors and limit the system’s generalizability. Arbitrary-resolution assimilation aims to overcome this limitation by allowing the seamless integration of data regardless of its resolution. This requires sophisticated algorithms capable of handling heterogeneous data inputs. The benefits are substantial: improved accuracy, reduced computational costs through avoiding pre-processing, and enhanced flexibility in accommodating diverse data sources. This approach is crucial for real-world applications where data often comes in inconsistent resolutions, such as in weather forecasting, climate modeling, and remote sensing, thus paving the way for more accurate and comprehensive models. However, challenges remain in developing robust and efficient algorithms that can handle the complexities of differing data resolutions and associated uncertainties. Future research should focus on addressing these challenges to fully realize the potential of arbitrary-resolution assimilation.
Fourier Neural Pros#
The heading “Fourier Neural Pros” suggests a discussion of the advantages of using Fourier transforms within neural networks. This likely involves exploring how Fourier methods improve upon traditional neural network architectures. Key potential advantages could include enhanced handling of spatial and temporal data, improved representation of periodic signals, and better generalization to unseen data. The application to data assimilation is crucial, likely leveraging Fourier’s ability to separate frequencies for efficient processing of diverse resolutions. Specific considerations might involve the choice of Fourier transform type (e.g., discrete or continuous), its integration with neural network layers (e.g., convolutional or fully connected), and the trade-offs between accuracy and computational cost. Ultimately, the analysis would demonstrate the superior performance of this “Fourier Neural Pros” approach compared to existing methods, potentially highlighted by quantifiable metrics and compelling visualizations.
DAM Module Design#
The Dynamic Alignment and Merge (DAM) module is a critical component of the Fourier Neural Processes (FNP) framework, designed to effectively integrate information from diverse sources. Its primary function is to reconcile the background forecast and observational data, which might originate from different resolutions, and to seamlessly combine this information into a unified representation. The module’s innovative approach involves dynamically aligning the feature spaces of the background and observations, achieving a consistent representation across different resolutions. This is crucial because directly merging data of varying resolutions would likely lead to suboptimal results and hinder the model’s ability to learn effectively. The dynamic filtering process, based on feature similarity, is cleverly designed to emphasize the most relevant features and suppress noise or less relevant signals, thus enhancing the model’s performance. The flexible structure of the DAM module is particularly well-suited for handling arbitrary-resolution data assimilation, highlighting its key advantage compared to traditional methods that rely on pre-processing steps that may introduce unwanted errors. By dynamically adapting to varying resolutions, the DAM module fosters the robustness and generalization ability of the FNP method, making it highly adaptable for real-world applications with often heterogeneous input data.
Generalization Ability#
The research paper’s strength lies in its exploration of the model’s generalization ability. The authors cleverly demonstrate that the Fourier Neural Process (FNP) excels at handling data assimilation tasks with arbitrary resolutions. This is a significant advancement, as existing methods often struggle with varying data resolutions. The impressive generalization is not limited to resolution; FNP also successfully handles tasks beyond data assimilation, specifically observational information reconstruction, without requiring additional fine-tuning. This adaptability highlights the robustness and flexibility of the FNP architecture. The experimental results showcasing these capabilities provide substantial evidence of the model’s capacity to generalize well beyond the training data distribution. The success in out-of-distribution generalization makes FNP a promising approach for real-world applications where data characteristics might vary significantly.
Future Research#
Future research directions stemming from this work on Fourier Neural Processes (FNP) for arbitrary-resolution data assimilation could focus on several key areas. Improving the model’s efficiency and scalability to handle even higher-resolution data and larger datasets is crucial for real-world applications. This may involve exploring more efficient neural architectures or incorporating techniques like model parallelism. Addressing the limitations of the current experimental setup, such as relying on simulated observations, is important for building trust in the model’s generalizability. Using real-world data would greatly improve the robustness and reliability of the FNP approach. Further investigation into handling uncertainty more effectively is necessary, perhaps by incorporating probabilistic forecasting methods. Finally, exploring the applicability of FNP to other data assimilation tasks beyond weather forecasting, such as oceanography or climate modeling, could unlock substantial benefits in various scientific domains. Developing a unified framework for both data assimilation and reconstruction tasks would streamline the workflow and improve model efficiency.
More visual insights#
More on figures

This figure shows a detailed overview of the Fourier Neural Processes (FNP) architecture for arbitrary-resolution data assimilation. It illustrates the different modules, including the unified coordinate transformation, spatial-variable functional representation using SetConv and neural Fourier layers, the dynamic alignment and merge (DAM) module, and the final MLP decoder. The figure highlights the flow of data and the interactions between the modules, providing a comprehensive visual representation of the FNP model.
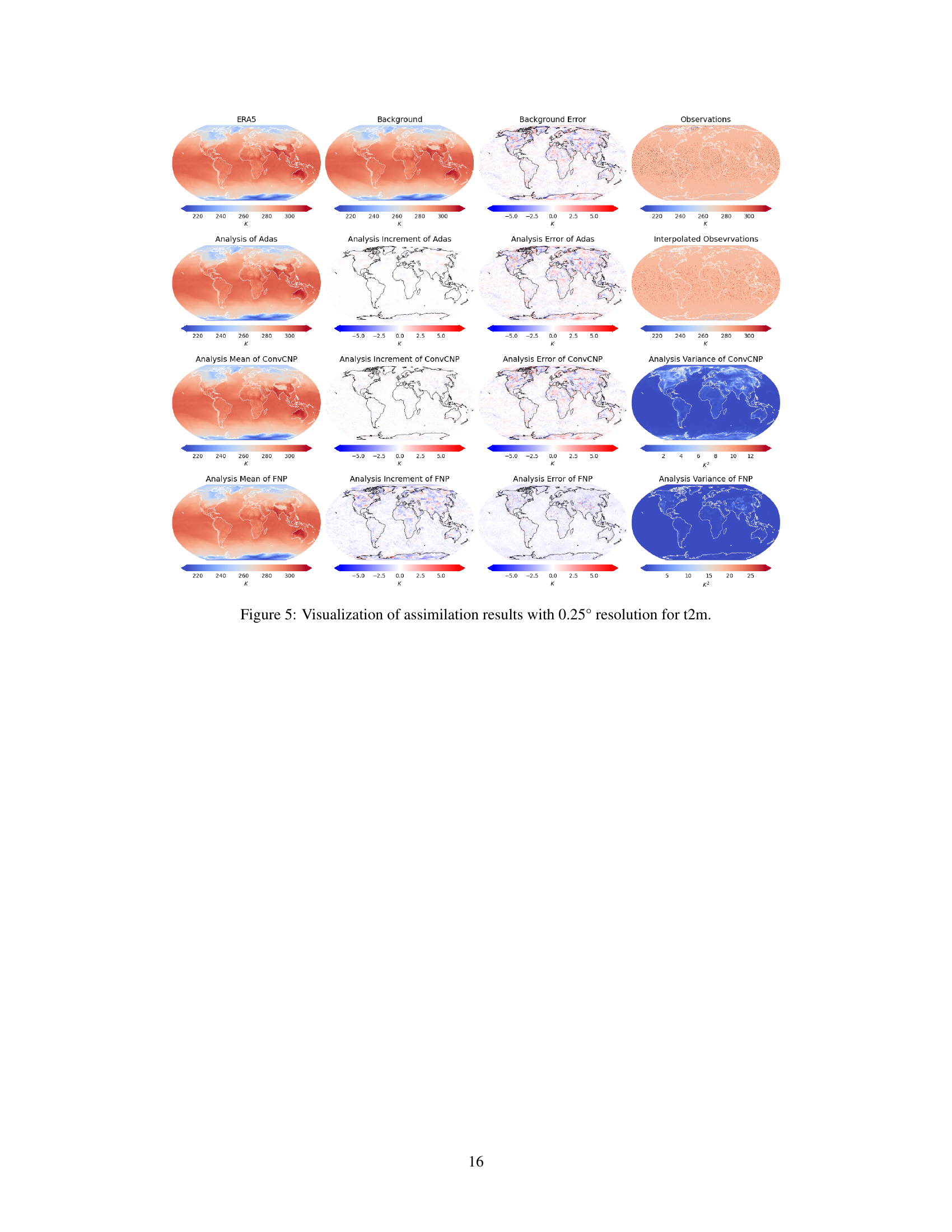
This figure visualizes the results of data assimilation for the variable q700 (specific humidity at 700 hPa) using four different models: ERA5 (ground truth), Adas, ConvCNP, and FNP. The visualization compares the models’ performance in terms of accuracy and ability to capture high-frequency information. It showcases ERA5, the background used for assimilation, the background error, the raw observations, the analysis generated by each model, the analysis increment (difference between the analysis and background), and the analysis error (difference between the analysis and ERA5). It also displays the analysis variance for ConvCNP and FNP, offering insight into the uncertainty associated with each model’s predictions. Notably, the figure highlights FNP’s success in capturing high-frequency information and reducing analysis error compared to the other methods.

This figure visualizes the results of data assimilation using different models on the u10 variable (10-meter zonal component of wind) with a resolution of 0.25°. It shows a comparison of ERA5 (ground truth), the background forecast, the background error, and the raw observations. The analysis results (estimated state of the atmosphere) from Adas, ConvCNP, and FNP are shown, including analysis increments (difference between analysis and background) and analysis errors (difference between analysis and ERA5). The analysis variance from ConvCNP and FNP is also displayed, indicating uncertainty estimates. The visualizations aim to highlight the performance differences of the models in handling different data resolutions and capturing high-frequency details.
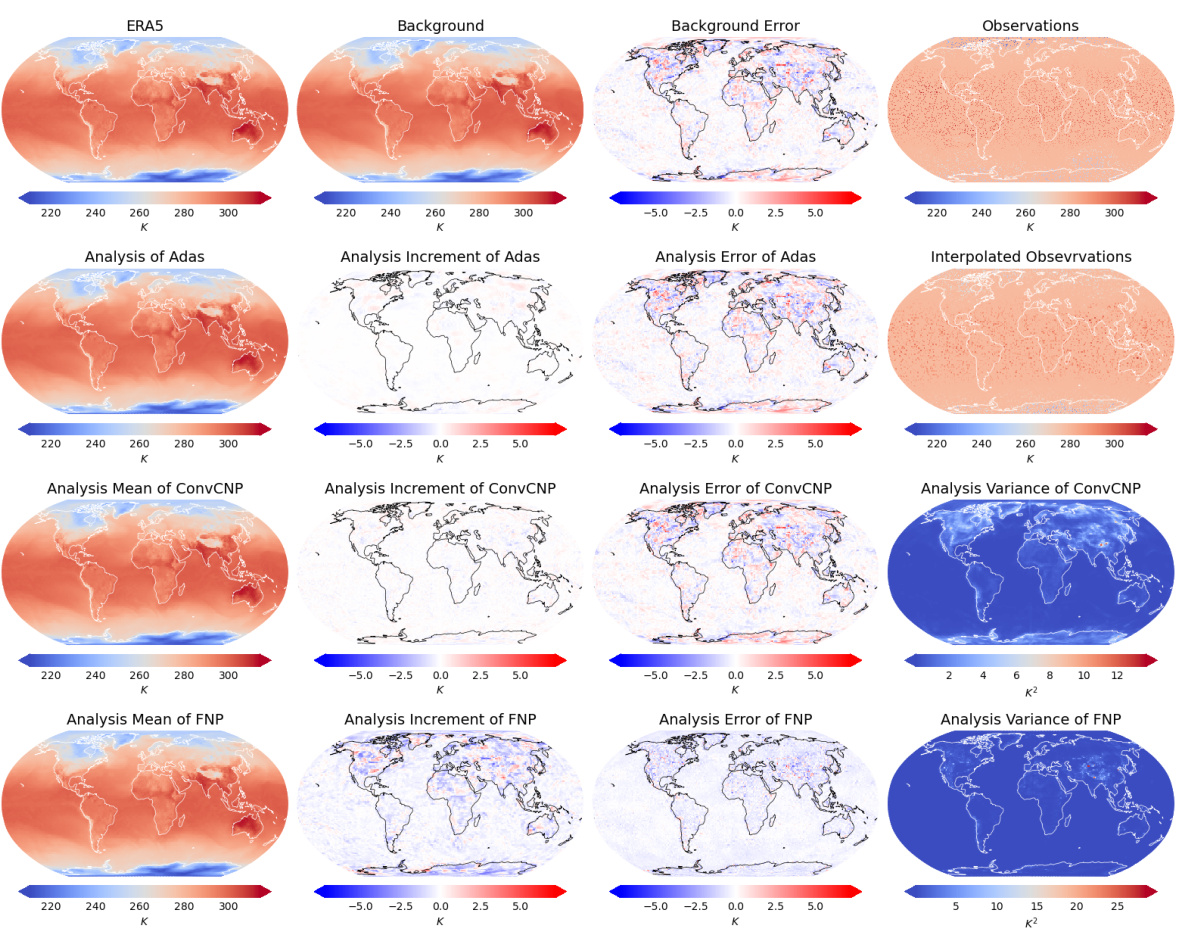
This figure visualizes the results of data assimilation using different methods (Adas, ConvCNP, and FNP) for the variable q700 (specific humidity at 700 hPa) at a specific time. It compares the ground truth (ERA5), background forecast, and observations with the analysis results, analysis increments, analysis errors, and analysis variance produced by each method. The visualization highlights the differences in accuracy and ability to capture high-frequency information between the methods, especially at a high resolution (0.25°).

This figure visualizes the results of data assimilation for the z500 variable (geopotential height at 500 hPa) using a resolution of 0.25°. It compares the results of four different methods: ERA5 (ground truth), Adas [10], ConvCNP [20], and the proposed FNP method. For each method, it shows the analysis (the estimated state), the analysis increment (the difference between the analysis and background), the analysis error (the difference between the analysis and the ground truth), and the analysis variance (an estimate of uncertainty in the analysis). The visualization provides a clear comparison of the accuracy and uncertainty of each method in capturing the spatial distribution of the geopotential height.
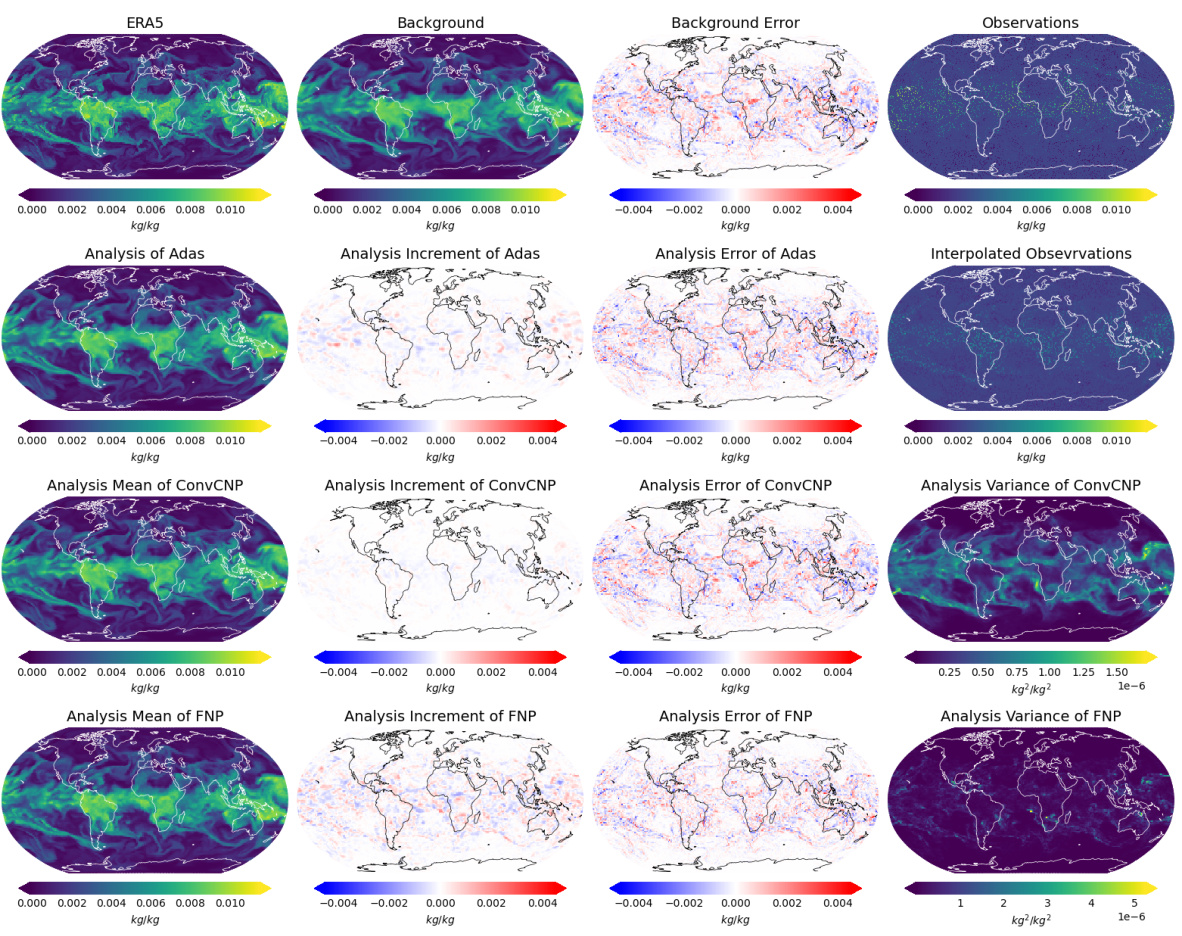
This figure visualizes the results of data assimilation for the variable q700 (specific humidity at 700 hPa) using different models (Adas, ConvCNP, and FNP). The top row shows the ground truth from ERA5, the background forecast, the error in the background forecast, and the sparse observational data. Subsequent rows display the analysis (assimilated result) for each model, the difference between the analysis and background (analysis increment), and the error between the analysis and ground truth (analysis error). The analysis variance is also displayed for ConvCNP and FNP. The visualization uses a 0.25° resolution for better detail.

This figure visualizes the results of data assimilation for the specific humidity at 700 hPa (q700) using different models. It compares the ERA5 reanalysis data (ground truth), model background, background error, and 0.25° resolution observations against the analysis produced by Adas, ConvCNP, and FNP. Each model’s analysis, analysis increment (difference between analysis and background), analysis error (difference between analysis and ERA5), and analysis variance are displayed. The visualization highlights how well each model captures the spatial distribution and high-frequency information, providing a visual comparison of their performance in data assimilation.
More on tables

This table presents a quantitative comparison of the analysis errors for different data assimilation methods across various resolutions (1.40625°, 0.703125°, and 0.25°). It compares the performance of the proposed Fourier Neural Processes (FNP) against other methods like Adas and ConvCNP. The results are broken down by metrics (MSE, MAE, and WRMSE) and specific variables (z500, t850, t2m, u10, v10, u500, v500, q700). Color-coding highlights improvements or degradations relative to the baseline resolution (1.40625°). The table also shows results with and without fine-tuning for certain models to highlight the impact of resolution adaptation.
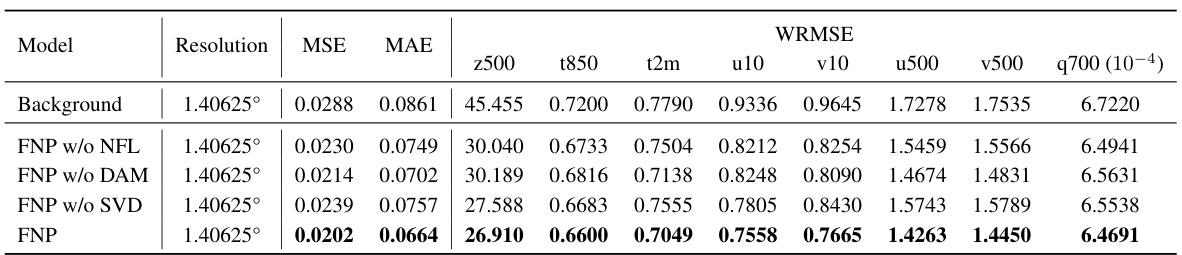
This table presents a quantitative comparison of the analysis errors for different data assimilation methods (FNP, ConvCNP, and Adas) across various resolutions (1.40625°, 0.703125°, and 0.25°). The metrics used for comparison include Mean Squared Error (MSE), Mean Absolute Error (MAE), and latitude-weighted Root Mean Square Error (WRMSE) for several key meteorological variables (z500, t850, t2m, u10, v10, u500, v500, and q700). The table highlights the best performing model at each resolution and shows whether the performance improved or worsened relative to the baseline resolution of 1.40625°. The results are presented both with and without additional fine-tuning for methods capable of handling varying resolutions.
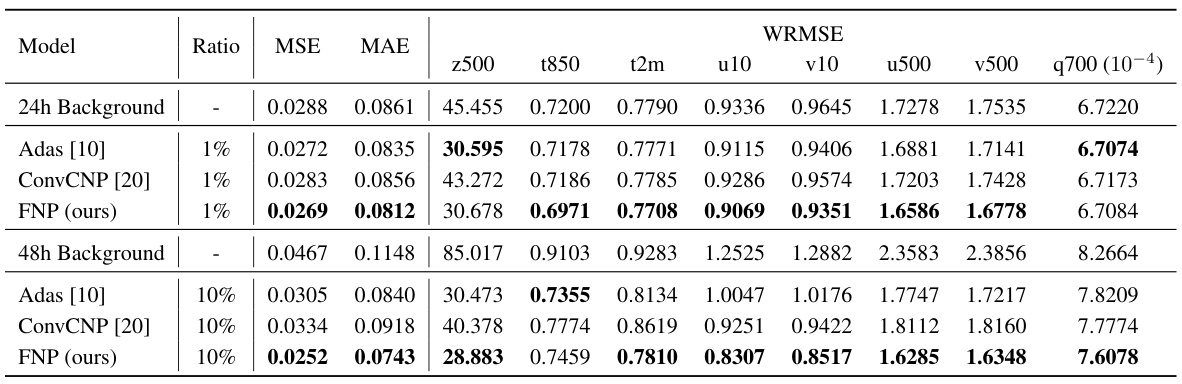
This table presents a quantitative comparison of the analysis errors of four different models (Adas, ConvCNP, FNP with and without fine-tuning) for assimilating observations with three different resolutions (1.40625°, 0.703125°, and 0.25°) onto a 24-hour forecast background with 1.40625° resolution. The metrics used for comparison are MSE, MAE, and WRMSE for several key weather variables. Color-coding highlights improvements or degradations in performance relative to the 1.40625° resolution baseline.
Full paper#