↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Reinforcement learning (RL) algorithms, especially Q-learning, often struggle with instability when using function approximation to handle large state and action spaces. This instability, known as the ‘deadly triad’, arises from the combination of off-policy learning, function approximation, and bootstrapping, leading to unreliable or divergent results. Existing solutions often require complex modifications or strong assumptions, limiting their practicality.
This paper introduces RegQ, a novel algorithm designed to overcome these limitations. RegQ incorporates a simple regularization term in the Q-learning update rule, ensuring convergence when linear function approximation is used. The authors rigorously prove the algorithm’s stability and convergence using recent analytical tools based on switching system models. They also provide an error bound on the solution, offering insights into the algorithm’s performance. Extensive experiments show that RegQ successfully converges in scenarios where standard Q-learning diverges.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning, particularly those working with function approximation. It directly addresses the instability and divergence issues plaguing Q-learning, offering a novel, convergent algorithm (RegQ). This opens doors for more robust and reliable RL applications in various fields. The proposed solution is theoretically sound, backed by rigorous mathematical proofs and supported by experimental validation, making it a valuable addition to the existing literature. Moreover, the use of a switching system model enhances analysis for similar algorithms.
Visual Insights#
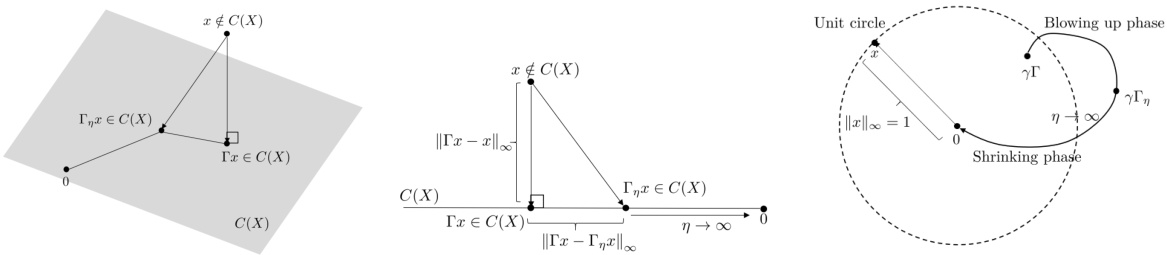
The figure illustrates how the regularized projection operator (Γη) behaves as the regularization parameter (η) varies. Panel (a) shows the standard projection, while (b) shows the effect of regularization. As η approaches infinity, the regularized projection shrinks to zero (the ‘shrinking phase’). Panel (c) provides an illustrative example of this effect in a one-dimensional case, highlighting how the projection’s bound changes with η.

This table presents the results of an experiment on the Mountain Car environment. The experiment compares the performance of the RegQ algorithm with different values of the regularization coefficient (η) and varying numbers of tiles used in tile coding to discretize the state space. The episode reward is shown, averaged over 100 test runs for each condition, demonstrating the effect of hyperparameter tuning on performance.
In-depth insights#
RegQ Algorithm#
The RegQ algorithm, a novel approach to Q-learning, addresses the instability issues inherent in using linear function approximation. By incorporating an appropriate regularization term, RegQ ensures convergence, a significant improvement over standard Q-learning. This stability is rigorously proven using a switching system model analysis. Empirical results demonstrate RegQ’s efficacy in environments where traditional methods diverge, validating the theoretical findings. A key aspect is its single time-scale nature, leading to faster convergence compared to two-time-scale alternatives. The algorithm’s simplicity and proven convergence make it a potentially valuable tool in reinforcement learning, especially for applications involving linear function approximation where traditional Q-learning struggles.
Convergence Analysis#
The Convergence Analysis section is crucial for validating the efficacy of the proposed regularized Q-learning algorithm (RegQ). It leverages the ordinary differential equation (ODE) approach, a common tool in stochastic approximation analysis. The authors construct upper and lower comparison systems, framing the RegQ update as a switched linear system. By demonstrating asymptotic stability for these bounding systems, they infer global asymptotic stability for RegQ itself. A key element is the incorporation of an appropriate regularization term, which is theoretically shown to ensure convergence. The analysis carefully addresses the challenges posed by the deadly triad in reinforcement learning, specifically focusing on off-policy learning with function approximation. Error bounds on the solution are derived, providing a measure of the algorithm’s accuracy and highlighting how regularization affects the final result. The use of switching systems and ODE analysis is a strong theoretical framework for understanding the algorithm’s behavior and its convergence properties.
Error Bound Analysis#
The heading ‘Error Bound Analysis’ suggests a section dedicated to quantifying the accuracy of the proposed algorithm. A thoughtful analysis would delve into how far the algorithm’s output might deviate from the true solution. This involves deriving a mathematical expression, or bound, that limits the maximum error. The analysis would likely consider factors like the regularization parameter, the choice of feature representation, and the properties of the underlying Markov Decision Process (MDP). A key insight would be whether the error bound shrinks as the algorithm runs longer, or if it remains constant. The impact of the regularization parameter on the error bound is also important: a larger parameter might introduce more bias but reduce variance. The error analysis should reveal the trade-off between bias and variance. The study might compare this error bound against existing Q-learning algorithms with linear function approximation to demonstrate improved accuracy. Finally, it should assess how these theoretical error bounds relate to practical performance observed in experiments.
Experimental Results#
The experimental results section of a research paper is crucial for validating the claims made by the authors. A strong experimental results section should clearly present the methodology used, including the datasets, metrics, and experimental setup. Visualizations such as graphs and tables should effectively communicate the findings, making it easy to understand the performance of the proposed method and to compare it against baselines. Key results should be highlighted, with specific attention to the aspects that confirm the paper’s central hypotheses. Moreover, the discussion of the results should be comprehensive, addressing both the successes and limitations. A thoughtful analysis of the results might include explanations for any unexpected findings and suggestions for future work. Statistical significance should be explicitly stated using appropriate metrics, ensuring the reliability of the findings. The overall goal is to provide convincing evidence to support the claims made in the paper, leaving the reader with a clear understanding of the method’s effectiveness and potential impact.
Future Research#
The paper’s ‘Future Research’ section would ideally delve into several promising avenues. Extending RegQ to handle nonlinear function approximation is crucial for broader applicability. Investigating the impact of different regularization techniques, beyond L2, and their effect on convergence and solution quality would provide valuable insights. A thorough empirical comparison with a wider range of RL algorithms and environments is needed to assess its true performance. Addressing the bias inherent in the linear function approximation and exploring ways to mitigate it would strengthen the algorithm. Finally, theoretical investigation into the algorithm’s sample complexity and the development of tighter error bounds are essential for further theoretical advancement. Exploring applications of RegQ in various real-world scenarios and comparing performance to existing state-of-the-art methods will determine its practical utility.
More visual insights#
More on figures

The figure shows the experimental results of four different Q-learning algorithms: CoupledQ, GreedyGQ, TargetQ, and RegQ. Two plots are presented. Plot (a) displays the results for the 0 → 20 environment from Tsitsiklis and Van Roy [1996], while plot (b) shows the results for the Baird seven-star counter example from Baird [1995]. The y-axis represents the error ||θ - θ*||, where θ is the estimated parameter vector and θ* is the optimal parameter vector, and the x-axis shows the number of steps or iterations. The shaded area represents the standard deviation or error bars. The results demonstrate that RegQ converges faster than the other algorithms in both environments.

This figure depicts a Markov Decision Process (MDP) with three states (s=1, s=2, s=3) and two actions (a=1, a=2). The transitions between states are represented by arrows, and the probabilities are implicitly defined in the paper. The feature vectors x(s,a) associated with each state-action pair are also shown. This MDP is a simple example used in the paper to illustrate a situation where the standard projected Bellman equation may not have a solution, but a regularized version does.

This figure shows two examples where standard Q-learning with linear function approximation fails to converge. (a) illustrates a simple Markov Decision Process (MDP) with two states (0 and 20), where Q-learning is known to diverge. (b) depicts the Baird seven-star counter example, a more complex MDP, also known for causing divergence in Q-learning with function approximation. These examples highlight the instability of Q-learning when combined with function approximation, a problem addressed by the proposed RegQ algorithm.
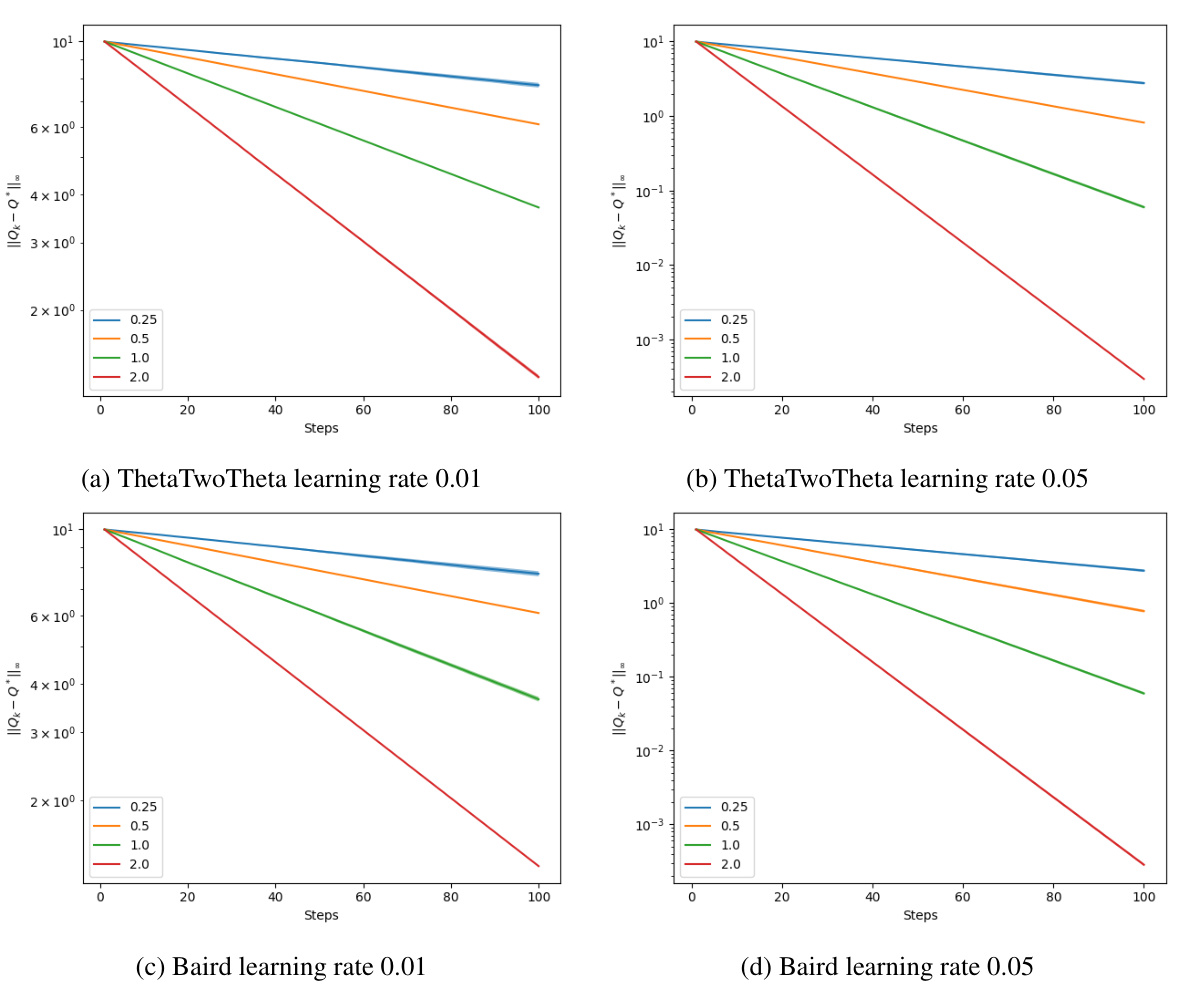
This figure shows the learning curves obtained with different learning rates (0.01 and 0.05) and regularization coefficients (η ∈ {2⁻², 2⁻¹, 1, 2}). The x-axis represents the number of steps, and the y-axis represents the error ||θ - θ*||. The curves show the convergence process of the RegQ algorithm in two different environments, namely the Tsitsiklis and Van Roy (0→20) environment and the Baird counter-example. The results demonstrate that the convergence rate improves as the regularization coefficient increases.
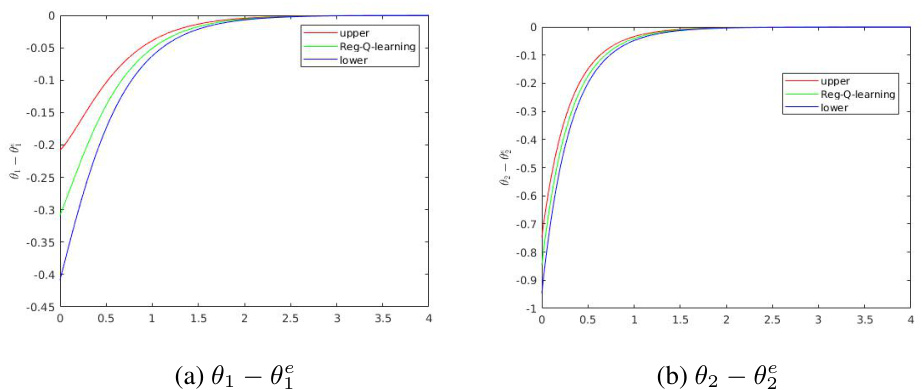
This figure shows the trajectories of the upper and lower systems for the regularized Q-learning algorithm. The trajectories of the original system are bounded by the trajectories of the upper and lower systems, illustrating the theoretical analysis of the algorithm’s convergence.
Full paper#



















