↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Sampling from high-dimensional, multimodal discrete distributions is challenging because gradient-based methods often get stuck in local optima. This is a significant problem in various machine learning applications where discrete variables are common, such as energy-based models and large language models. Current methods struggle to explore the entire distribution effectively.
This research introduces the Automatic Cyclical Sampler (ACS), a novel gradient-based discrete sampling method that addresses these challenges. ACS uses cyclical schedules to automatically adjust the step size and proposal distribution, balancing exploration (finding new modes) and exploitation (characterizing current modes). This approach leads to significant improvements in sampling efficiency and accuracy, overcoming the local optima limitation of existing methods. The method has been proven theoretically, showing convergence guarantees, and demonstrated empirically across a wide range of complex multimodal distributions. This work sets a new standard for discrete sampling with notable implications for numerous machine learning applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with discrete distributions, especially in high-dimensional settings like deep learning. It offers a novel solution to the persistent problem of local optima trapping in gradient-based discrete sampling, a common issue limiting the efficiency and accuracy of existing methods. The proposed method’s theoretical guarantees and empirical superiority on various complex multimodal distributions make it a significant advancement for many machine learning applications. Its automatic tuning capability greatly reduces manual effort, increasing usability and making it readily adaptable for diverse real-world problems.
Visual Insights#

This figure compares the performance of different sampling methods on a 2D multimodal distribution. The ground truth distribution is shown, along with results from a random walk sampler, DMALA (a gradient-based method with manual tuning), AB (another gradient-based sampler), and the proposed ACS method. The visualization demonstrates that while the random walk sampler finds all modes, it is inaccurate. Gradient-based methods are effective at characterizing individual modes but get easily trapped in local optima. Only the proposed ACS method accurately and efficiently finds and characterizes all modes.

This table presents the test log-likelihood scores for deep convolutional EBMs, estimated using Annealed Importance Sampling (AIS). The results compare the performance of the proposed Automatic Cyclical Sampler (ACS) against three other gradient-based discrete sampling methods: Gibbs-with-Gradient (GWG), Discrete Metropolis Adjusted Langevin Algorithm (DMALA), and Any-scale Balanced Sampler (AB). Lower log-likelihood values indicate better model performance. The table shows that ACS consistently achieves better or comparable results compared to the other methods across different datasets (Static MNIST, Dynamic MNIST, Omniglot, Caltech). GWG results are sourced from a previous study by Grathwohl et al. (2021).
In-depth insights#
Auto Cyclical Sched#
The concept of ‘Auto Cyclical Sched’ in the context of gradient-based discrete sampling suggests an algorithm that automatically adjusts sampling parameters over time. This is crucial because naive gradient-based methods often get stuck in local optima of multimodal distributions. Automatic scheduling implies the system dynamically adapts the step size and balance parameters without manual tuning, enhancing efficiency and accuracy. A cyclical approach likely involves alternating between phases of exploration (larger steps to find new modes) and exploitation (smaller steps to accurately characterize the found modes). The ‘auto’ aspect is key—reducing the need for manual hyperparameter tuning, which can be time-consuming and dataset-specific. The success of this method hinges on the algorithm’s ability to automatically determine the optimal cycle length, the transition points between exploration and exploitation phases, and the precise parameter adjustments within each phase. Theoretical guarantees and/or empirical evidence of convergence and superior performance compared to existing methods would be critical to validating the approach. It represents a significant step towards making gradient-based discrete sampling more robust and practical for complex real-world applications.
Multimodal Sampling#
Multimodal sampling, focusing on discrete distributions, presents a significant challenge due to the inherent discontinuities and presence of multiple modes. Standard gradient-based methods often fail, getting trapped in local optima. This paper addresses this limitation by introducing an innovative automatic cyclical scheduling algorithm. The key is a dynamic balance between exploration and exploitation, achieved through cyclical variation of step size and a balancing parameter within each cycle. This approach allows the sampler to efficiently discover and characterize multiple modes, effectively escaping local optima. The algorithm incorporates an automated tuning mechanism that adapts to different datasets, minimizing manual intervention and hyperparameter tuning. The theoretical analysis provides non-asymptotic convergence guarantees, adding a strong theoretical foundation. Finally, empirical results across various tasks (including RBMs, EBMs, and LLMs) demonstrate the superiority of the proposed method over existing state-of-the-art gradient-based samplers, showcasing its improved accuracy and efficiency.
Convergence Rate#
The authors delve into the crucial aspect of convergence rate, providing a non-asymptotic convergence and inference guarantee for their proposed method within the context of general discrete distributions. This signifies a notable advancement compared to prior research, which primarily established asymptotic convergence or relative convergence rate bounds. The theoretical analysis, employing techniques to address the challenges of varying step sizes and balancing parameters across cycles, is a key contribution. Uniform ergodicity of the Markov chain is established, proving convergence to the target distribution with a defined rate. The convergence rate is shown to be geometric, providing a quantitative measure. However, the assumptions underpinning these results, including the strong concavity of the energy function, deserve attention. The practical implications of these assumptions and how they might impact real-world applications are worthy of further investigation. The theoretical findings provide a strong foundation, but the real-world performance and sensitivity to these assumptions warrant careful study.
EBM Learning#
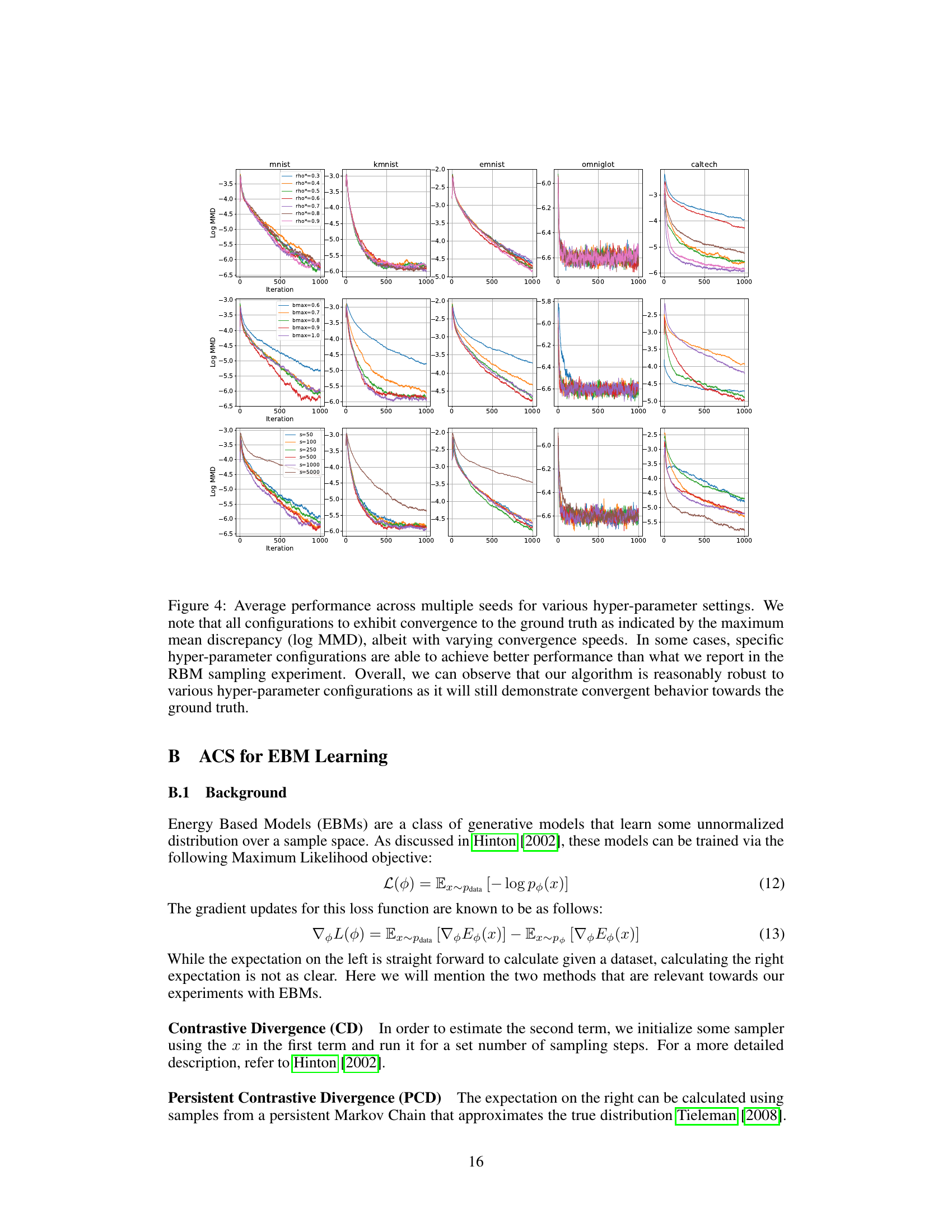
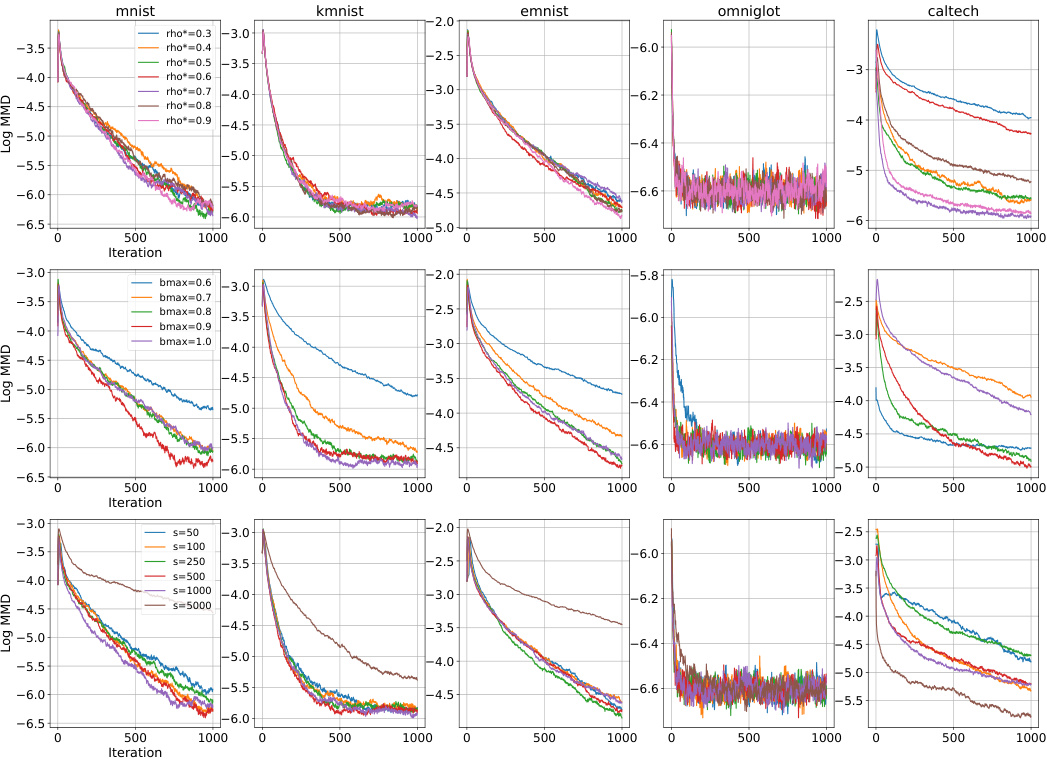
The section on “EBM Learning” would detail the application of the proposed Automatic Cyclical Sampler (ACS) to training Energy-Based Models (EBMs). It would likely highlight the challenges of sampling from complex, high-dimensional EBM distributions, emphasizing the susceptibility of gradient-based methods to becoming trapped in local modes. The authors would then present ACS as a solution, showcasing its ability to efficiently explore the multimodal landscape of EBMs and improve the accuracy of gradient estimations during training. Key aspects would include the cyclical schedule’s role in balancing exploration and exploitation of the EBM’s energy surface, the automatic tuning mechanism’s capacity to adapt across different datasets and model architectures, and the use of techniques such as Persistent Contrastive Divergence (PCD) to estimate gradients. Quantitative results comparing ACS against other state-of-the-art gradient-based discrete samplers, possibly including metrics like log-likelihood, are expected. Furthermore, the discussion might include qualitative insights, perhaps showing generated samples from EBMs trained using ACS, demonstrating the superiority of ACS in capturing diverse modes and detailed characteristics of the underlying distributions. Theoretical analysis might offer non-asymptotic convergence guarantees for ACS in this context, adding rigor to the empirical findings.
Future Directions#
Future research could explore several promising avenues. Extending the automatic cyclical scheduling to other gradient-based discrete sampling methods beyond the specific algorithm presented in the paper would broaden the applicability and impact of the technique. Investigating the optimal design of cyclical schedules themselves—including the frequency, amplitude, and shape of the cycles—is crucial for further improving sampling efficiency and accuracy. Theoretical analysis could be deepened to provide stronger convergence guarantees and address scenarios with more complex or less well-behaved energy functions. Moreover, empirical evaluations on a wider range of datasets and tasks—including high-dimensional problems and different types of discrete distributions—would strengthen the claims and identify potential limitations. Finally, exploring applications in new fields could reveal additional benefits of this approach. For example, its utility in Bayesian inference, combinatorial optimization, and reinforcement learning could be significant. Addressing these areas would advance both theoretical understanding and practical applications of gradient-based discrete sampling.
More visual insights#
More on figures

This figure compares different sampling methods on a 2D multimodal distribution. It shows that a random walk sampler can explore all modes but lacks detailed characterization, while gradient-based methods like DMALA and AB can characterize specific modes but get stuck in local optima. The proposed ACS method (Ours) is shown to efficiently find and characterize all modes.

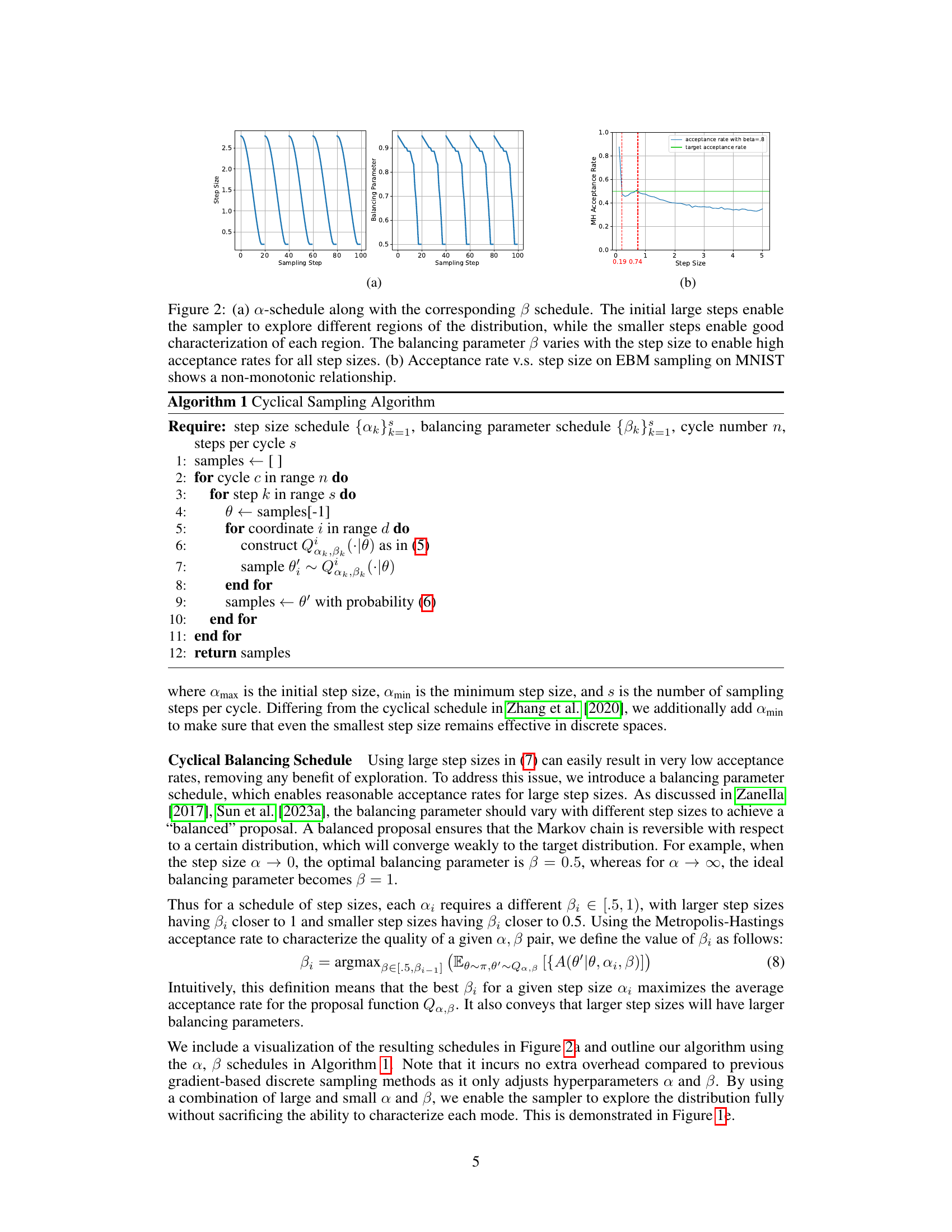
This figure visualizes the cyclical schedules for the step size (α) and balancing parameter (β). Panel (a) shows how α starts large, allowing exploration of different modes, and gradually decreases, enabling detailed characterization of each mode. The β schedule complements α by adjusting the proposal distribution for each step size, maintaining a high acceptance rate. Panel (b) demonstrates a non-monotonic relationship between acceptance rate and step size in the context of EBM sampling on MNIST dataset.
This figure compares the performance of different sampling methods on a 2D multimodal distribution. It shows that a simple random walk sampler can explore all modes but lacks accuracy. Gradient-based methods, such as DMALA and AB, show better accuracy but may get stuck in local modes. The authors’ proposed method (ACS) demonstrates improved performance by efficiently exploring and characterizing all modes of the multimodal distribution.
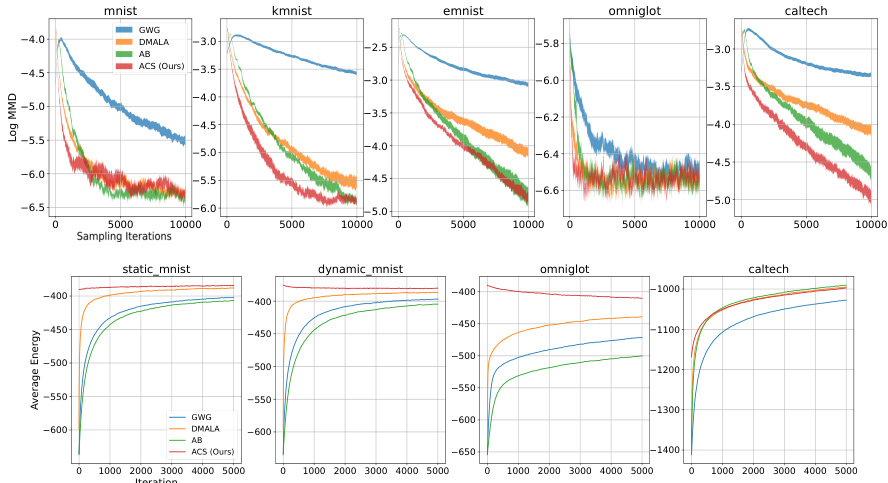
This figure compares the performance of various sampling methods (GWG, DMALA, AB, and ACS) on Restricted Boltzmann Machines (RBMs) and deep Energy-Based Models (EBMs). The top row shows the convergence to the ground truth for RBMs, measured by the Maximum Mean Discrepancy (MMD), averaged over 11 trials with standard error bars. The bottom row presents the convergence speed on EBMs. The results demonstrate that ACS achieves competitive performance compared to the other baselines for both RBMs and EBMs.

This figure shows an uneven multimodal distribution where one mode has significantly higher probability mass than others. The caption emphasizes that sampling only from the high-probability mode would provide an inaccurate representation of the entire distribution. This highlights the challenge of gradient-based samplers that can become stuck in local modes, motivating the need for the proposed automatic cyclical scheduling method in the paper.

The figure displays the convergence speed and the Maximum Mean Discrepancy (MMD) between samples generated by different methods and ground truth for Restricted Boltzmann Machines (RBMs) and deep Energy-Based Models (EBMs) across multiple datasets. The top row shows MMD values over sampling iterations for RBMs on various datasets (MNIST, kMNIST, eMNIST, Omniglot, and Caltech). The bottom row presents the average energy (a measure of convergence) over iterations for EBMs on the same datasets. The results indicate that the proposed Automatic Cyclical Sampler (ACS) method performs competitively with other state-of-the-art methods in sampling from multimodal distributions.

This figure compares the performance of different sampling methods (GWG, DMALA, AB, and ACS) on Restricted Boltzmann Machines (RBMs) and deep Energy-Based Models (EBMs). The top row shows the convergence to the ground truth (measured by MMD) for RBMs across different datasets (MNIST, kMNIST, eMNIST, Omniglot, and Caltech). The bottom row shows the convergence speed (average energy) for deep EBMs on the same datasets. The results demonstrate that the proposed Automatic Cyclical Sampler (ACS) achieves competitive performance compared to the existing baselines, showcasing its effectiveness in sampling complex multimodal distributions.

This figure compares different sampling methods on a 2D multimodal distribution. It showcases the limitations of random walk samplers (noisy and lacks detail), manually tuned gradient-based methods (easily trapped in local modes), and highlights the advantages of the proposed ACS method (efficiently finds and characterizes all modes).
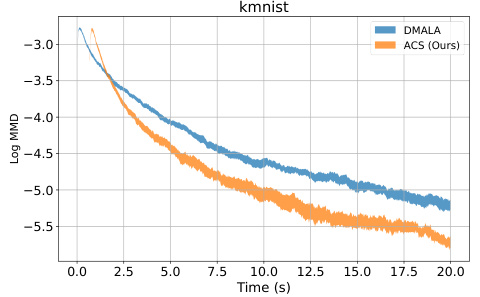
This figure compares the performance of various sampling methods (GWG, DMALA, AB, and ACS) on Restricted Boltzmann Machines (RBMs) and deep Energy-Based Models (EBMs). The top row shows the convergence to the ground truth for RBMs, measured by the Maximum Mean Discrepancy (MMD) between the generated samples and the samples generated by Block Gibbs sampling. The bottom row displays the convergence speed for deep EBMs, showing the average energy of samples over time. The results indicate that the ACS method is competitive with other state-of-the-art methods in both RBM and EBM sampling tasks.

This figure compares different sampling methods on a 2D multimodal distribution. It shows that a random walk sampler can find all modes but lacks detail, while gradient-based methods (DMALA and AB) can characterize specific modes but get stuck in local optima. The proposed ACS method effectively finds and characterizes all modes.

This figure compares different sampling methods on a 2D multimodal distribution. The ground truth distribution is shown alongside results from a random walk sampler, DMALA, AB, and the proposed ACS method. It highlights the ability of ACS to efficiently and accurately characterize all modes, unlike other methods which either miss modes or get stuck in local optima.

This figure compares the performance of different sampling methods on a 2D multimodal distribution. The ground truth distribution is shown alongside results from a random walk sampler, DMALA, AB, and the proposed ACS method. It highlights that while random walk can explore all modes, its characterization is poor. Gradient-based methods like DMALA and AB efficiently characterize a specific mode but get trapped in local modes. The proposed ACS method overcomes this limitation by efficiently exploring and accurately characterizing all modes.
More on tables
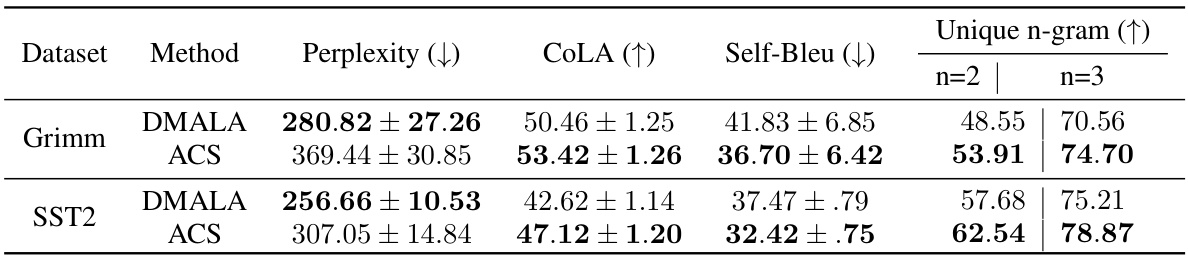
This table presents the results of an empirical evaluation of the generated sentences using two different methods: DMALA and ACS. The table shows that ACS outperforms DMALA across various metrics related to the diversity of the generated sentences. The metrics include perplexity (lower is better), COLA (higher is better), Self-Bleu (lower is better), and the percentage of unique 2-grams and 3-grams (higher is better). The results indicate that ACS generates more diverse and unique sentences compared to DMALA.

This table compares the performance of DMALA and ACS samplers on an uneven multi-modal distribution. It shows the KL divergence (a measure of difference between two probability distributions) and average energy of samples generated by each method. Lower KL divergence indicates better accuracy in capturing the target distribution. The results demonstrate ACS’s superior performance in accurately capturing all the modes, even with uneven weighting of the modes in the target distribution.
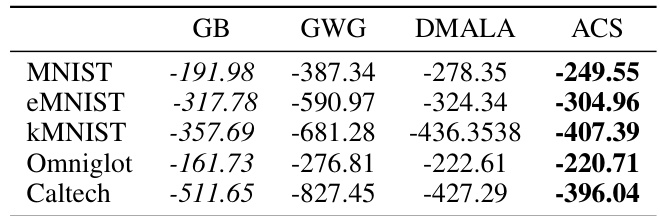
This table shows the test set log-likelihoods of deep convolutional EBMs trained using different gradient-based discrete sampling methods. The log-likelihoods were estimated using Annealed Importance Sampling (AIS). The table compares the performance of the proposed Automatic Cyclical Sampler (ACS) against three baselines: Gibbs-with-Gradient (GWG), Discrete Metropolis Adjusted Langevin Algorithm (DMALA), and Any-Scale Balanced Sampler (AB). The results show that ACS achieves better log-likelihood scores than the baselines across all four datasets (Static MNIST, Dynamic MNIST, Omniglot, Caltech).
Full paper#