↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many scientific domains rely on learning dynamical systems from time series data. However, a model with low test error may still fail to reproduce the true dynamics or associated statistical properties like Lyapunov exponents. This is especially problematic when dealing with chaotic systems. This paper highlights the limitations of traditional generalization analysis in this context, emphasizing the need for a new framework that captures underlying physical measures.
This paper proposes a novel ergodic theoretic approach to address this gap. The researchers introduce dynamics-aware notions of generalization, which consider the reproduction of dynamical invariants and analyze how different types of neural network parameterizations learn these invariants. They rigorously show how adding Jacobian information during training significantly improves statistical accuracy. The authors verify these results on various chaotic systems, demonstrating the method’s effectiveness in capturing the underlying dynamics and accurately predicting statistical moments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with dynamical systems and machine learning. It directly addresses the critical issue of statistical accuracy in learned models, a problem frequently encountered in complex systems. By providing rigorous generalization bounds and highlighting the importance of Jacobian information, it offers valuable guidance for improving the reliability and trustworthiness of data-driven models. This work opens exciting avenues for developing more physically accurate and robust machine learning models.
Visual Insights#

The figure compares the results of three different models for simulating the Lorenz system: the true solution, a model trained with mean-squared error (MSE), and a model trained with Jacobian information. The MSE model produces atypical orbits that deviate from the true system’s behavior, while the Jacobian model accurately reproduces both the short-term and long-term dynamics, including the probability distribution of orbits. This highlights the importance of including Jacobian information during training to ensure statistical accuracy in learned dynamical systems.

This table compares the statistical properties of the true Lorenz system against those learned by neural networks trained using two different loss functions: Mean Squared Error (MSE) and Jacobian matching (JAC). The comparison includes the Wasserstein-1 distance between the empirical distributions, the difference in Lyapunov exponents (LEs), and the difference in average states. The results show that the JAC loss leads to significantly better agreement with the true system’s statistics than the MSE loss.
In-depth insights#
Ergodic Generalization#
The concept of “Ergodic Generalization” in the context of learning dynamical systems from time series data proposes a novel framework that addresses the limitations of conventional generalization measures. Instead of solely focusing on prediction accuracy, this framework emphasizes the ability of a learned model to capture the underlying statistical properties of the true dynamical system. This is crucial because a model that accurately predicts short-term behavior might fail to reproduce the system’s long-term statistical properties, such as invariant measures or Lyapunov exponents. The ergodic nature of many dynamical systems is central to this concept, as it implies that time averages along a typical trajectory converge to ensemble averages. The core idea behind ergodic generalization is to ensure the learned model faithfully emulates these statistical properties, going beyond simple point-wise prediction accuracy. This approach leads to more robust and physically meaningful models for understanding complex dynamical systems.
Neural ODE Limits#
Neural Ordinary Differential Equations (NODEs) offer a powerful approach to model dynamical systems by representing the system’s evolution as a continuous-time process. However, NODEs are not without limitations. A key challenge is their sensitivity to the choice of numerical solver used for integration. Different solvers can lead to varying degrees of accuracy, and the choice of solver can significantly impact the model’s ability to generalize to unseen data. The expressiveness of NODEs can also be limited, especially when modeling complex dynamics with high dimensionality or intricate interactions. Furthermore, training NODEs effectively can be computationally expensive, particularly when dealing with long time series. Careful consideration must be given to hyperparameter tuning, and training stability is often a concern. Finally, a theoretical understanding of NODEs’ generalization properties remains incomplete, making it difficult to provide guarantees on the accuracy of their predictions, particularly in chaotic systems. These various limitations highlight the importance of further research to fully understand the potential and pitfalls of using NODEs in practice.
Jacobian Regularization#
Jacobian regularization, in the context of training neural networks for dynamical systems, is a crucial technique for enhancing the models’ ability to capture the underlying dynamics accurately. It addresses the issue of generalization failure, where models with low test error still fail to reproduce the true system’s behavior, particularly its long-term statistical properties and invariants like Lyapunov exponents. By incorporating Jacobian information (the derivative of the vector field) into the loss function, the training process is directly guided to learn not only the system’s trajectory but also its sensitivity to perturbations. This helps ensure that the learned model better emulates the true system’s behavior, improving the statistical accuracy of its predictions. The results indicate that adding Jacobian information significantly increases the accuracy of statistical measures (probability distributions and Lyapunov exponents) and the fidelity of reproduced attractors, demonstrating the effectiveness of this regularization for learning complex dynamical systems.
Shadowing Dynamics#
Shadowing dynamics, in the context of chaotic systems, refers to the remarkable ability of a slightly perturbed trajectory to remain close to an actual trajectory of the system for an extended period. This concept is crucial for understanding the reliability of numerical simulations and data-driven models of complex, chaotic systems. In such systems, small errors in initial conditions or numerical integration can rapidly amplify, leading to significant divergence. Shadowing theory provides a framework for assessing whether a numerically computed or learned trajectory faithfully represents the underlying dynamics, even if it’s not exactly the same. The existence and prevalence of shadowing orbits are central to the concept of statistical accuracy of learned models of chaotic systems. Models which reproduce relevant statistical properties like Lyapunov exponents or invariant measures while failing to perfectly match individual orbits demonstrate the significance of the shadowing property in capturing the essence of the dynamics. This notion is tightly connected to the broader question of generalization in machine learning applications. A model’s ability to generate statistically accurate results, rather than exact reproductions of training data, is essential for many applications and reflects the fundamental robustness of the underlying dynamical system.
Generative Models#
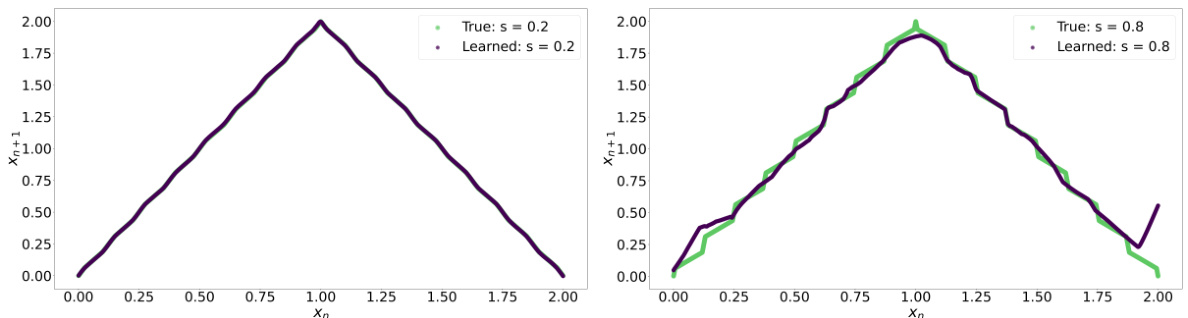
Generative models offer a powerful approach to learning complex systems by directly modeling the underlying probability distribution of the data. Unlike discriminative methods that focus on prediction, generative models aim to capture the essence of the system’s dynamics, enabling both sampling of new states and analysis of the system’s inherent structure. In the context of chaotic systems, generative models can be particularly useful in representing the complex, high-dimensional probability distributions that often characterize these systems. However, standard generative models may not fully capture temporal dynamics; they might not accurately reproduce dynamical invariants like Lyapunov exponents, and might struggle with issues like training instability in the presence of chaotic behavior. Dynamic generative models, which explicitly incorporate the temporal dynamics into the generative process, offer a promising solution to these challenges. These models combine the power of generative modeling with the ability to reproduce dynamical properties, potentially leading to a better understanding and simulation of chaotic systems. The success of such models hinges on appropriate choices of architectures and training methods that can effectively manage the complexities introduced by the chaotic nature of the underlying systems. Future research could explore the development of novel generative models specifically tailored to chaotic dynamics, along with rigorous theoretical analysis to assess their ability to capture and reproduce key features of the system.
More visual insights#
More on figures

This figure compares the learned and true Lyapunov exponents (LEs) for the Lorenz ‘63 system. The LEs were computed using the QR algorithm over 30,000 time steps, starting from 10,000 random initial states. The ‘MSE’ LEs are from a neural ODE model trained with mean squared error loss, while the ‘JAC’ LEs are from a model trained with a Jacobian loss function (which includes Jacobian information). The plot shows that the Jacobian-trained model (‘JAC’) more accurately reproduces the true LEs, particularly the stable LE, which is negative. This result demonstrates the importance of Jacobian information for learning statistically accurate models of chaotic systems.
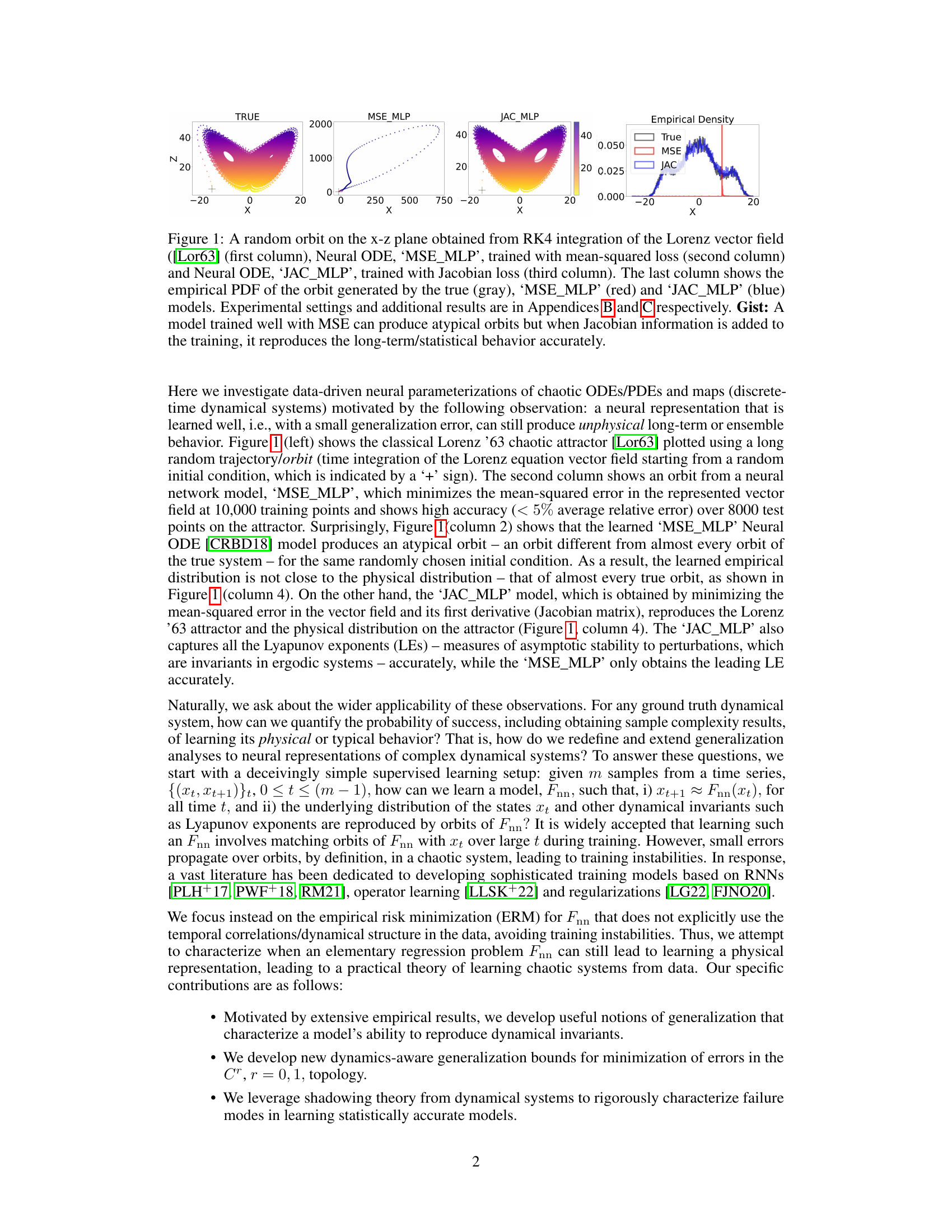
This figure compares the performance of three different models in replicating the Lorenz system’s dynamics. The first column shows a true orbit of the Lorenz system, generated using the Runge-Kutta 4th order method (RK4). The second and third columns depict orbits generated by Neural ODE models trained using mean squared error (MSE) and Jacobian loss respectively. The last column presents the probability density functions (PDFs) of the x-coordinate for the three models, showing a closer match between the true PDF and the Jacobian-based model. The figure highlights the improved accuracy in capturing long-term statistical behavior when incorporating Jacobian information during training.

This figure compares the performance of three different models in replicating the Lorenz attractor. The first column shows the actual Lorenz attractor generated using the Runge-Kutta method. The second column shows the results obtained using a neural ordinary differential equation (NODE) model trained with the mean squared error (MSE) loss function. The third column shows the same NODE model but trained using a Jacobian loss function, which includes the Jacobian matrix (derivative of the vector field) in the loss calculation. The last column displays the probability density function (PDF) of the orbits produced by each model. The figure highlights that the MSE loss function can generate orbits that significantly differ from the true Lorenz attractor’s behavior. In contrast, the Jacobian loss function leads to a much more accurate representation of the attractor’s long-term and statistical behavior.
This figure compares the performance of two Neural ODE models trained on the Lorenz system: one using mean squared error (MSE) and the other using Jacobian loss. The first three columns display random orbits of the Lorenz system obtained from numerical integration (RK4), MSE-trained model, and Jacobian-trained model. The last column illustrates the probability density functions (PDFs) for the orbits generated by the true system, MSE model, and Jacobian model. The figure shows that a well-trained MSE model can still generate atypical orbits, whereas the Jacobian-trained model accurately reproduces the long-term statistical behavior of the true system.
This figure compares the performance of two neural ordinary differential equation (NODE) models trained on the Lorenz system. The first model (MSE_MLP) is trained using mean squared error loss, while the second model (JAC_MLP) incorporates Jacobian information in the loss function. The figure shows that while the MSE_MLP model can reproduce short-term dynamics accurately, it fails to capture the long-term statistical properties of the system. In contrast, the JAC_MLP model accurately captures both short-term and long-term behavior.

This figure compares the performance of three different models in reproducing the dynamics of the Lorenz system. The first column shows a true orbit obtained through numerical integration of the Lorenz equations. The second and third columns show orbits generated by neural ordinary differential equation (NODE) models trained with mean squared error (MSE) and Jacobian loss, respectively. The fourth column presents probability density functions (PDFs) for each model compared to the true PDF, highlighting that the model trained with Jacobian loss much better captures the true statistical properties of the Lorenz attractor.
This figure compares the performance of three different models in replicating the Lorenz attractor: the true Lorenz system, a neural ODE model trained with mean squared error (MSE), and a neural ODE model trained with Jacobian information. The MSE model, while having low test error, produces atypical orbits that deviate from the true system’s behavior, whereas the Jacobian-trained model accurately reproduces both the orbits and their statistical properties. This illustrates the point that low test error alone is insufficient; capturing underlying physical behavior necessitates additional training considerations.

This figure compares the results of simulating the Lorenz system using different methods. The first column shows a trajectory obtained using the standard Runge-Kutta 4th order method. The second column shows a trajectory generated by a neural ordinary differential equation (NODE) model trained using mean squared error (MSE). The third column shows a trajectory from a NODE model trained using both MSE and Jacobian information (JAC). The fourth column shows the probability density functions (PDFs) of the trajectories generated by each method, compared to the true PDF. The figure demonstrates that the MSE-trained NODE produces trajectories that are qualitatively different from the true system, while the JAC-trained NODE accurately reproduces the long-term statistical behavior of the system.

This figure compares the performance of different neural ODE models in reproducing the Lorenz attractor. The first three columns show random orbits generated by the true Lorenz system (using RK4 integration), a model trained with a mean squared error loss (MSE_MLP), and a model trained with a Jacobian loss (JAC_MLP). The last column shows the probability density functions (PDFs) for each. The MSE_MLP, while accurate in the short term, produces orbits that deviate significantly from the true system’s long-term behavior and statistical properties. In contrast, the JAC_MLP model trained with Jacobian information accurately reproduces the long-term behavior and the statistical moments of the true system.
More on tables
This table shows the hyperparameter choices used in the numerical experiments for various chaotic systems. The hyperparameters include the number of epochs for training, the time step used in the simulation, the hidden layer width and number of layers in the neural network architecture, the training and testing set sizes, the type of neural network used (ResNet or MLP), and the lambda (λ) value used in the Jacobian-matching loss function.

This table presents the Lyapunov exponents learned by neural ordinary differential equation (NODE) models trained using the mean squared error (MSE) loss for multi-step prediction. It compares the results for two different neural network architectures, MLP and ResNet, and for different numbers of timesteps (k) used in the unrolling of the dynamics during training. Lyapunov exponents are a measure of the rate of separation of nearby trajectories in a dynamical system, and thus this table provides insight into how accurately the NODE models are learning the underlying dynamics of the systems.

This table compares the true statistical measures (Wasserstein-1 distance, Lyapunov exponents, and average state) of the Lorenz ‘63 system with those learned by neural ordinary differential equation (NODE) models trained using either mean-squared error (MSE) loss or Jacobian-matching loss. It shows the differences between the true and learned quantities for different model types and training sequence lengths (k).

This table compares the true Lyapunov exponents for several chaotic systems (tent maps, Lorenz ‘63, Rössler, hyperchaos, Kuramoto-Sivashinsky) with those obtained from neural ODE models trained using two different loss functions: mean squared error (MSE) and Jacobian-matching. The comparison highlights the impact of including Jacobian information in the training process on the accuracy of learning the dynamical invariants of the systems. The results indicate that Jacobian-matching leads to significantly more accurate estimates of the Lyapunov exponents, particularly for more complex systems. Each system is represented by a vector of Lyapunov exponents reflecting the asymptotic exponential rate of separation or convergence of nearby trajectories in its phase space.

This table presents the Lyapunov spectra obtained from a latent stochastic differential equation (SDE) model trained on the Lorenz ‘63 system. The spectra are computed using both the Euler-Maruyama and RK4 numerical integration methods. The comparison highlights the impact of including the diffusion term (stochasticity) in the model on the accuracy of the computed Lyapunov exponents. The results suggest that the stochasticity affects the Lyapunov spectrum, indicating potential differences in the model’s representation of the system dynamics.
This table compares the statistical properties of the true Lorenz ‘63 system with those learned by neural networks trained using different loss functions. Specifically, it contrasts the Wasserstein-1 distance (a measure of distribution similarity) between the true and learned systems, the differences in Lyapunov exponents (measures of chaos), and the differences in the average state values for orbits of length 500. This provides a quantitative comparison of how accurately different training methods capture the statistical properties of a chaotic system.
This table compares the statistical properties of the true Lorenz ‘63 system with those learned by neural networks trained using different loss functions. It shows the Wasserstein-1 distance between the true and learned probability distributions of orbits, the difference in the Lyapunov exponents, and the difference in the means of the state variables (x, y, z). The results highlight the impact of different loss functions on the statistical accuracy of the learned models. MSE (mean squared error) loss leads to larger discrepancies compared to JAC (Jacobian matching) loss, indicating that incorporating Jacobian information during training is crucial for learning statistically accurate models.
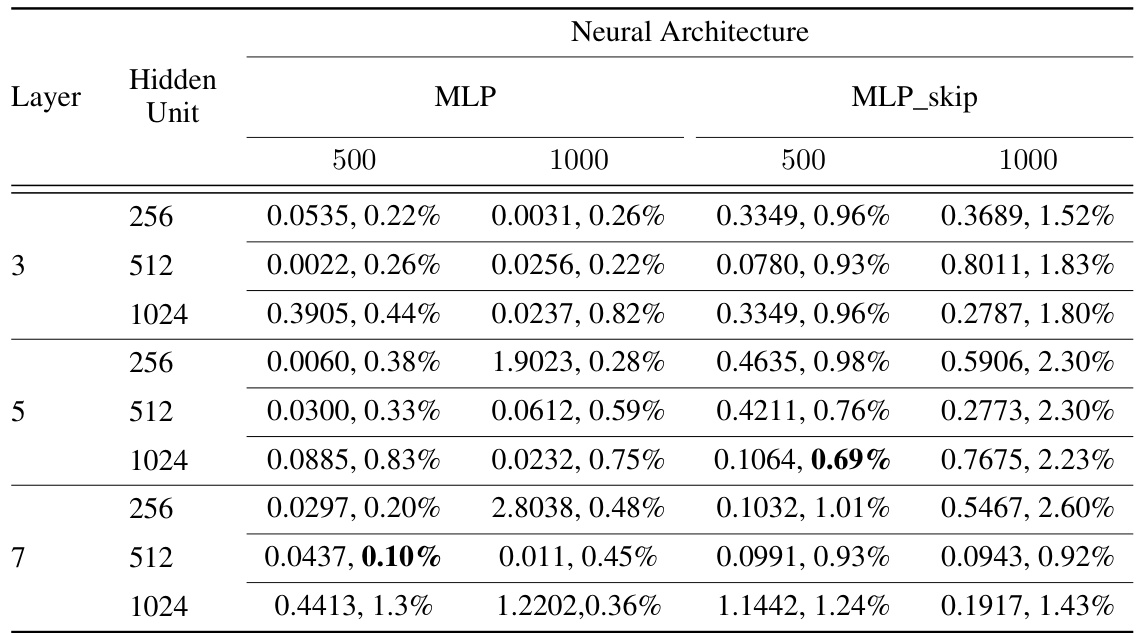
This table presents the results of a hyperparameter search for training Neural ODEs with MLPs using mean squared loss and the AdamW optimization algorithm. The search explored batch size, weight decay, hidden layer depth and width. The table shows test loss and relative error for each combination, highlighting the optimal settings that minimize relative error.
Full paper#