↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training large language models (LLMs) efficiently requires overcoming significant memory and communication challenges in distributed training. Existing methods, like ZeRO, offer limited options and often struggle with heterogeneous network setups where intra-group communication outperforms inter-group communication. This paper aims to address these limitations by proposing improved strategies for LLM training.
The authors introduce PaRO (Partial Redundancy Optimizer), a novel framework that offers refined model state partitioning (PaRO-DP) and tailored collective communication (PaRO-CC). PaRO-DP provides more trade-off options between memory and communication costs compared to existing strategies, improving training speed. PaRO-CC optimizes communication by leveraging intra- and inter-group performance differences. Experiments show that PaRO improves training speed significantly, up to 266% faster than ZeRO-3. The paper provides a guideline for selecting the best PaRO strategy, ensuring minimal performance loss.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language model (LLM) training because it introduces novel strategies for optimizing data parallelism. The PaRO framework significantly improves training speed, offering practical solutions to address memory and communication bottlenecks common in distributed LLM training. The findings open new avenues for optimizing existing and future LLM training frameworks, especially for those using heterogeneous network architectures.
Visual Insights#
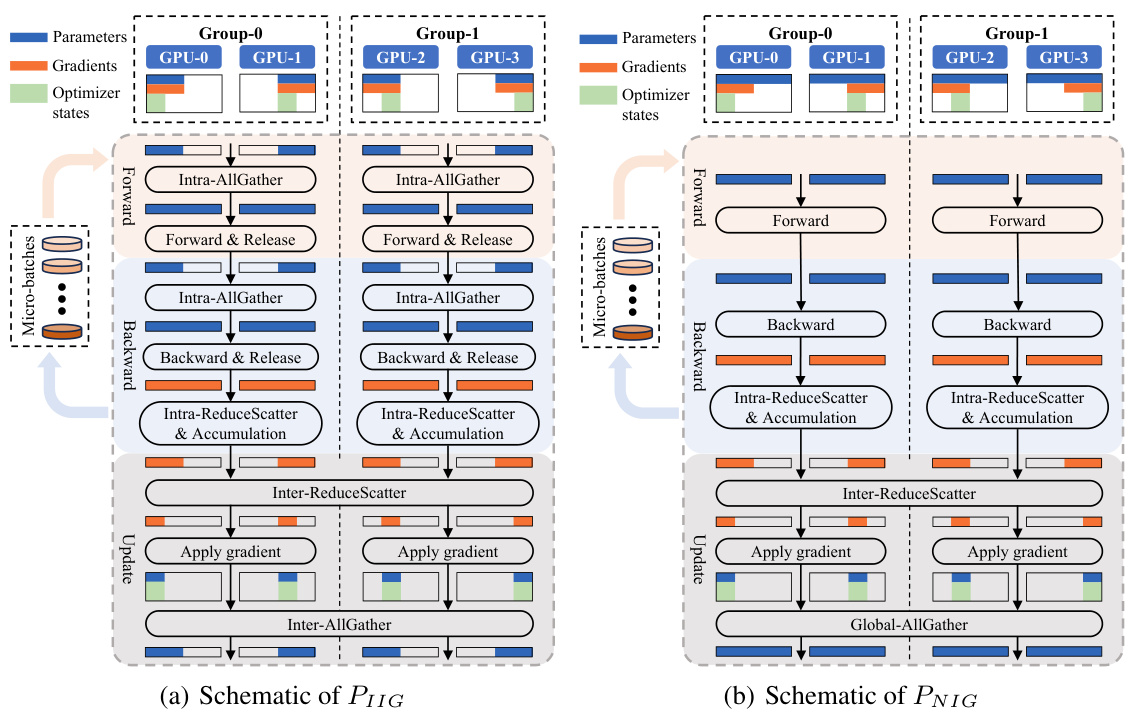
This figure shows two schematics illustrating the PaRO-DP (Partial Redundancy Optimizer-Data Parallelism) training strategy using four GPUs divided into two groups. Schematic (a) depicts the PIIG strategy (no parameter partitioning, intra-group gradient partitioning, global optimizer state partitioning). Schematic (b) shows the PNIG strategy (no parameter partitioning, intra-group gradient partitioning, global optimizer state partitioning). Both diagrams detail the forward pass, backward pass, gradient accumulation and update steps, highlighting intra-group and inter-group communication operations with specific prefixes. The figure demonstrates the proposed PaRO-DP’s ability to optimize memory and communication costs by strategically partitioning model states.

This table systematically lists all 27 possible combinations of partitioning strategies for model parameters (p), gradients (g), and optimizer states (os) across three levels of granularity: no partitioning (N), intra-group partitioning (I), and global partitioning (G). Each combination is represented as Pp+g+os, where P, g, and os represent the partitioning strategies for parameters, gradients, and optimizer states, respectively. A checkmark indicates effective combinations identified by the authors, while a cross indicates strategies eliminated based on the authors’ analysis of the trade-off between memory and communication costs.
In-depth insights#
PaRO: DP Strategy#
The PaRO (Partial Redundancy Optimizer) data parallelism (DP) strategy offers a novel approach to training large language models (LLMs) by rethinking the trade-off between memory and communication costs. Unlike existing methods that rely on a single partitioning strategy, PaRO introduces a refined model state partitioning, providing multiple options to balance these costs based on specific hardware configurations and LLM sizes. This flexibility is crucial, especially in heterogeneous environments where intra- and inter-group communication speeds differ significantly. By carefully managing redundancy, PaRO-DP aims to minimize inter-group communication, thus accelerating the overall training process. The core innovation lies in the tailored training procedures, which adapt to the chosen partitioning strategy, ensuring efficient memory utilization while avoiding redundant communication. A key aspect is the guideline for selecting the optimal strategy, based on quantitative calculations, thus eliminating the need for extensive experimentation and potentially reducing training time. This methodical approach, combined with the potential to enhance efficiency for partial parameter training and PEFT methods, makes PaRO-DP a significant advancement in LLM training optimization.
Communication Gaps#
Analyzing communication inefficiencies in large language model (LLM) training reveals significant performance bottlenecks. Heterogeneous network architectures, common in large-scale GPU clusters, introduce disparities between intra-group (high-speed) and inter-group (lower-speed) communication. This disparity significantly impacts collective communication operations (all-reduce, all-gather, etc.) frequently employed in data parallel training strategies. Strategies like ZeRO, while effective at reducing memory costs, often exacerbate these communication gaps due to their reliance on frequent global synchronization steps. Addressing these gaps requires innovative approaches beyond traditional techniques. This necessitates a shift toward refined model state partitioning strategies to minimize unnecessary inter-group communication, and possibly, clever network topology restructuring to fully exploit intra-group bandwidth. Techniques that can minimize global communication while maximizing local processing are key to achieving substantial improvements in LLM training efficiency.
PaRO-DP: Design#
The PaRO-DP design centers on optimizing data parallel training of large language models (LLMs) by addressing memory and communication cost trade-offs. It cleverly leverages the disparity between intra- and inter-group communication speeds within a cluster, introducing a novel set of strategies that refine model state partitioning. This partitioning goes beyond traditional approaches, offering more choices and flexibility in the allocation of parameters, gradients, and optimizer states across GPUs. A key element is the introduction of partial redundancy, allowing for faster intra-group communication at the cost of some memory increase. This innovative approach is supported by a quantitative guideline for selecting the most effective strategy based on specific hardware and model characteristics. The design is notable for its systematic consideration of memory-communication trade-offs and its adaptability to varying training scenarios, such as full-parameter and partial-parameter training, ultimately leading to significant LLM training speed improvements.
PaRO-CC: Topology#
PaRO-CC’s innovative topology reimagines collective communication in distributed training, addressing the performance bottleneck of heterogeneous networks. Instead of a simple ring topology, PaRO-CC structures communication in two layers: intra-group and inter-group. This hierarchical design leverages high-speed intra-group connections (e.g., NVLink) within each GPU machine or switch, significantly reducing the reliance on slower inter-group communication (e.g., RDMA over Ethernet). By carefully orchestrating the communication flow between these layers—executing intra-group and inter-group operations in parallel wherever possible—PaRO-CC minimizes latency and maximizes throughput. This strategy allows for greater scalability and efficiency, especially in large-scale clusters with varying levels of network connectivity. The intelligent re-arrangement of the communication topology is key; it’s adaptive and adaptable, tailoring to the specific architecture of the GPU cluster, thereby improving overall training speed and reducing training time. The results demonstrate a substantial improvement in efficiency compared to the traditional ring structure, illustrating the practical value of this topology-focused approach to optimizing collective communications.
Scaling Experiments#
A robust ‘Scaling Experiments’ section would delve into how the model’s performance changes with increasing resources. This would involve systematically varying the number of GPUs and observing the impact on metrics such as training throughput, memory usage, and communication overhead. Detailed graphs visualizing these relationships are crucial, showing any deviations from linear scaling, and potentially identifying bottlenecks. The analysis should carefully consider the trade-offs between scalability and cost-efficiency, evaluating whether the gains from additional resources justify the increased expenses. The experiment setup should be described in detail, including hardware specifications, software versions, and training hyperparameters, ensuring reproducibility. A comparison with other state-of-the-art models is vital to establish its competitive advantage in handling large-scale datasets. The results should be analyzed in the context of different model sizes and training objectives, highlighting which scaling strategies prove most effective under various scenarios. Finally, a discussion on limitations of scalability, including potential communication and synchronization challenges, is vital for a holistic perspective.
More visual insights#
More on figures

This figure illustrates the PaRO-DP strategy using a cluster with four GPUs divided into two groups. It shows the computation and communication flow for a global step (incorporating gradient accumulation). Panel (a) shows the PIIG strategy and panel (b) shows the PNIG strategy. The figure highlights the intra- and inter-group communication aspects of each strategy using specific prefixes for each collective communication primitive. This helps in visualizing how PaRO-DP optimizes the communication operations by performing intra-group operations before inter-group operations, thus reducing the communication overhead in heterogeneous network environments.
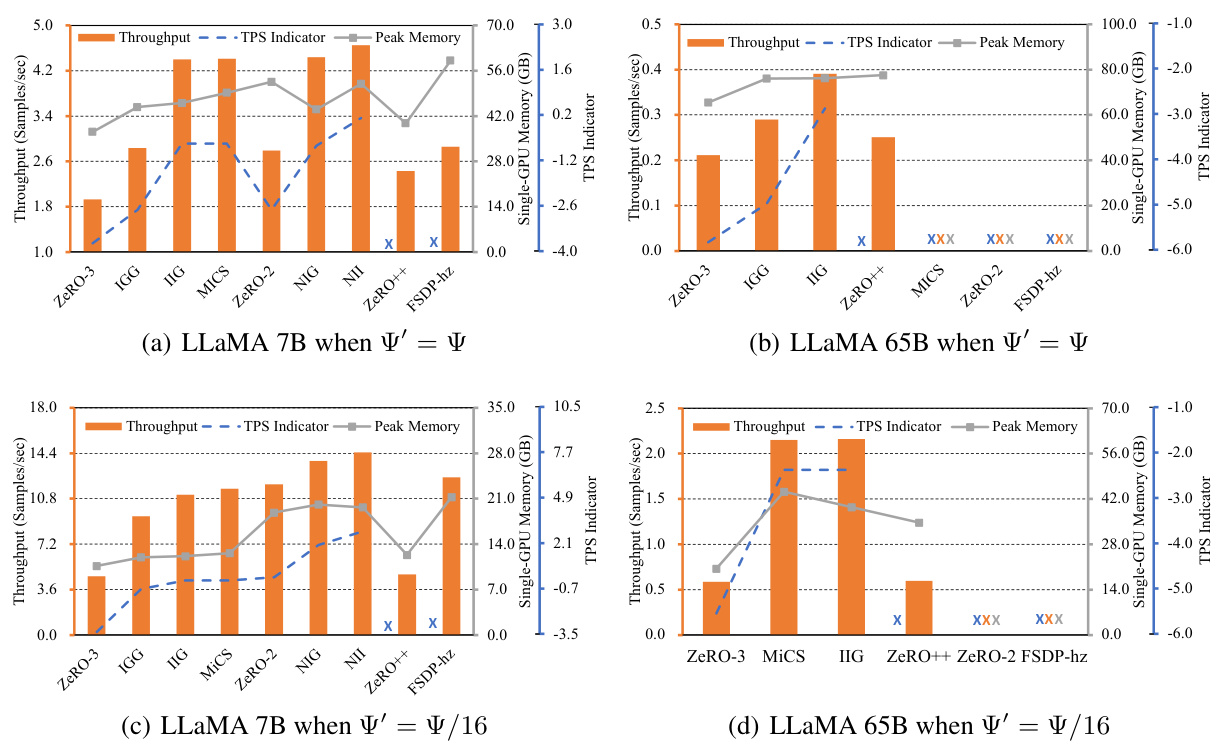
This figure displays the throughput and memory usage during the training of LLaMA models with different numbers of trainable parameters. Four different scenarios are shown, varying both model size (7B and 65B parameters) and the ratio of trainable parameters to total parameters (100%, 1/16). The x-axis represents the different training strategies used, including PaRO strategies and existing methods (ZeRO, MiCS, FSDP-hz, ZeRO++). The y-axis shows throughput and single-GPU memory usage. The blue dashed line indicates the trend of the throughput indicator (TPS, calculated with log(1/T)) predicted by the guideline presented in the paper, while the crosses denote out-of-memory (OOM) errors. The figure illustrates how the choice of strategy affects both training speed and memory consumption under different parameter scaling scenarios.
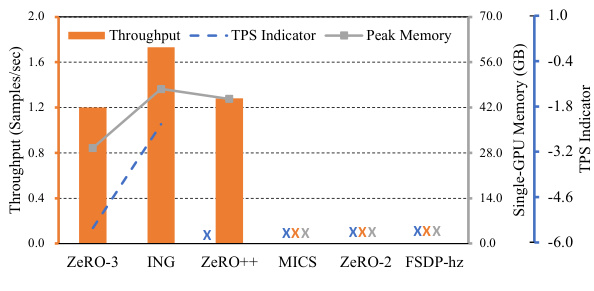
This figure shows the throughput, TPS indicator (log(1/T)), and peak memory usage for different model parallel training strategies in a PEFT scenario with LLaMA-65B model. The results highlight the superior performance of PaRO-DP strategies over existing approaches, indicating improvements in training speed and memory efficiency.

This figure compares the collective communication time of the traditional Ring topology and the proposed PaRO-CC method, as the number of GPUs increases from 16 to 128. It shows that PaRO-CC significantly reduces the communication time compared to the Ring topology, especially with a larger number of GPUs. This improvement is due to the efficient utilization of intra- and inter-group communication within PaRO-CC.
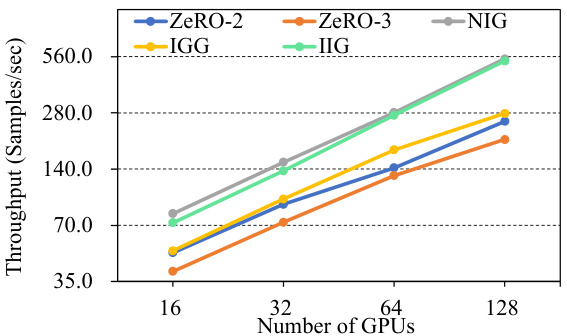
The figure shows the throughput of different training strategies (ZeRO-2, ZeRO-3, NIG, IGG, and IIG) as the number of GPUs increases from 16 to 128. It illustrates the scalability and performance of each strategy in a data parallel setting. The throughput is measured in samples per second.

This figure compares the training convergence curves of PaRO and ZeRO-3 using the LLaMA-7B language model. It demonstrates that the different PaRO strategies (NIG, IGG, IIG) achieve comparable convergence to the baseline ZeRO-3 method, indicating that the proposed PaRO optimization techniques do not negatively impact model training performance. The y-axis shows the loss, while the x-axis represents the training step.

This figure schematically shows how the Partial Redundancy Optimizer (PaRO) Data Parallelism (PaRO-DP) works in a cluster of four GPUs divided into two groups. It illustrates the computation and communication steps during a global training step using gradient accumulation. The diagrams highlight the intra-group and inter-group communications using specific prefixes (e.g., ‘Intra-AllGather’, ‘Inter-ReduceScatter’) for each collective communication primitive, illustrating the differences between the PIIG and PNIG strategies of PaRO-DP.

This figure illustrates the PaRO-DP strategy using two different model partitioning schemes (PIIG and PNIG) within a cluster of 4 GPUs divided into 2 groups. It shows the data flow and communication operations (intra- and inter-group) during a single global training step, including the forward pass, backward pass, gradient accumulation and gradient application phases. The visualization highlights the differences between PIIG and PNIG in terms of parameter and gradient partitioning, showcasing how PaRO-DP optimizes communication costs by leveraging intra-group communication whenever possible.
More on tables

This table shows how data blocks are distributed among GPUs based on different partitioning strategies: No partitioning, Intra-group partitioning, and Global partitioning. For each strategy, it specifies the indices of the data blocks that reside on a given GPU within a group and across different groups.
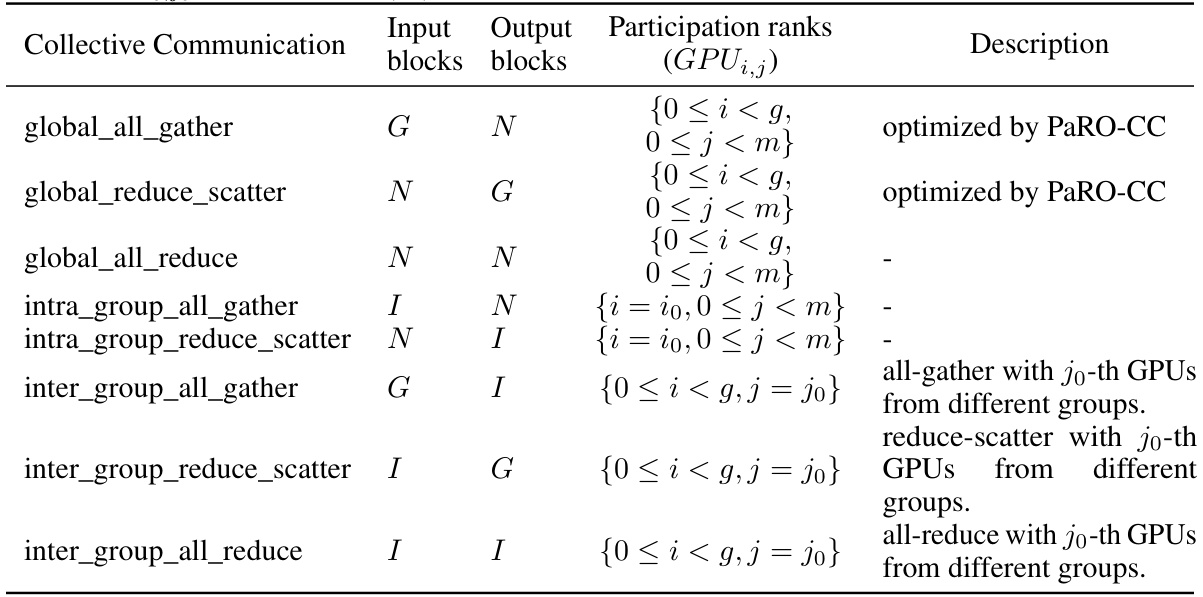
This table details the collective communication operations used for synchronization between blocks of different partitioning in the PaRO-DP framework. It shows the input and output blocks, participation ranks (GPU indices), and a description of each operation (global all-gather, global reduce_scatter, etc.), indicating how they are optimized by PaRO-CC.

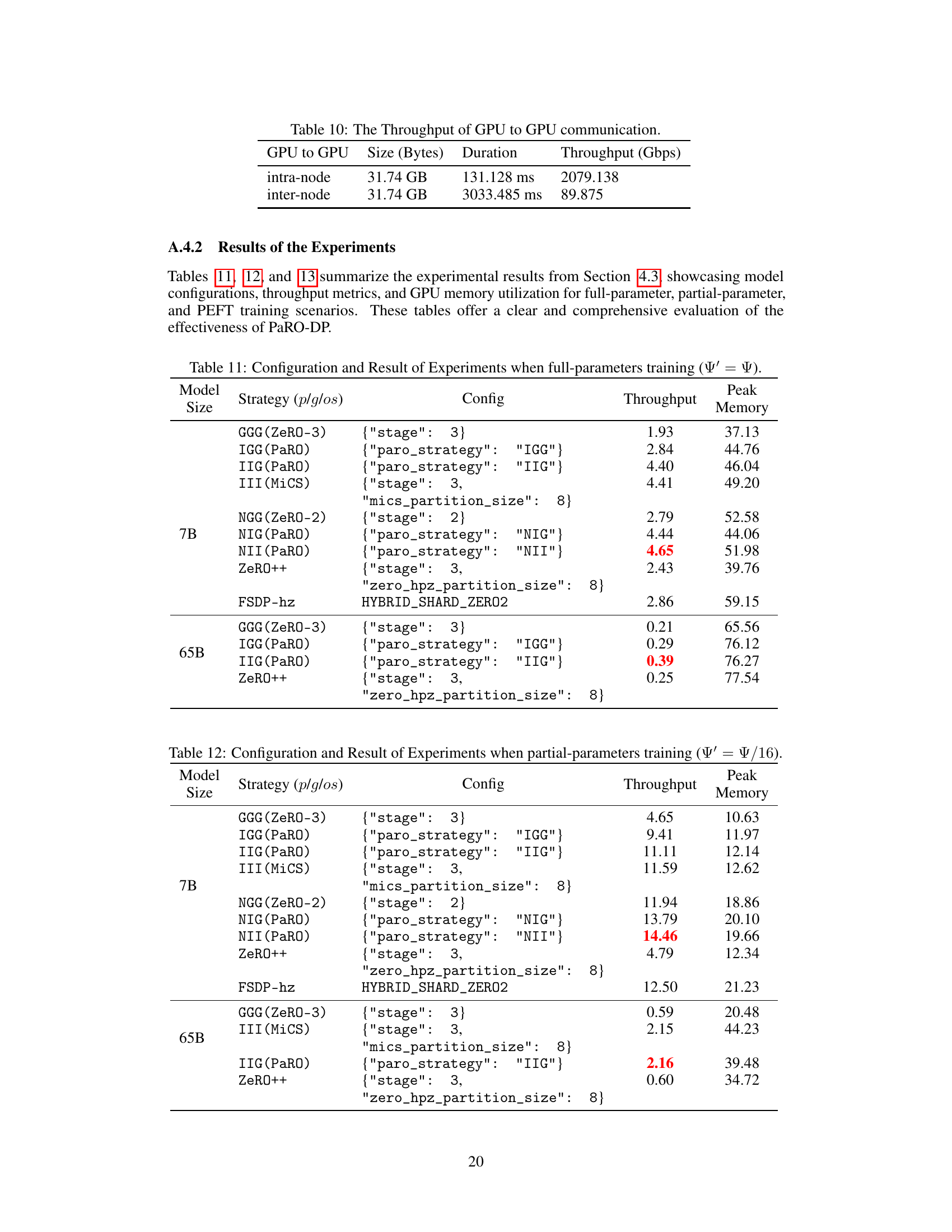
This table presents the results of training LLaMA-7B with different numbers of trainable parameters (full parameters, Ψ’=Ψ; partial parameters, Ψ’=Ψ/16). It compares various strategies in terms of throughput (1/T, samples per second) and peak GPU memory usage (Mem(GB)). The table allows for the comparison of different approaches under different memory constraints.

This table presents all possible combinations of partitioning strategies for model parameters (p), gradients (g), and optimizer states (os) across three levels of granularity: no partitioning (N), intra-group partitioning (I), and global partitioning (G). Each combination is represented as Pp+g+os (e.g., NNN, IIG), indicating the partitioning level for each component. The table highlights combinations identified as effective and those deemed ineffective, based on the analysis presented in the paper. Ineffective strategies were eliminated based on an analysis of memory usage and communication costs, considering the tradeoffs between these two aspects. The effective strategies form the basis of the PaRO-DP approach.

This table presents the training throughput (1/T) and GPU memory usage for the LLaMA-7B model under two different scenarios: full-parameter training (Ψ’ = Ψ) and partial-parameter training (Ψ’ = Ψ/16). It compares various PaRO-DP strategies against existing methods like ZeRO and MiCS, showing the throughput and peak memory used by each strategy. The results highlight the effectiveness of PaRO-DP in improving training throughput while maintaining reasonable memory consumption.

This table presents the results of training throughput (1/T) and GPU memory usage for the LLaMA-7B model under two different scenarios: full-parameter training (Ψ’ = Ψ) and partial-parameter training (Ψ’ = Ψ/16). It compares various PaRO-DP strategies against existing methods such as ZeRO-2, ZeRO-3, MiCS, and FSDP-hz. The table helps demonstrate the performance and memory efficiency improvements achieved with PaRO-DP, particularly in the partial-parameter training case, which is important for efficiency. Note that 1/T is a measure of training speed.

This table presents all possible combinations of model states partitioning strategies (Parameter, Gradient, Optimizer state) across three levels of granularity (No partitioning, Intra-group partitioning, Global partitioning). Each combination is evaluated for effectiveness, with a checkmark indicating effective strategies and a cross indicating ineffective strategies based on the insights from the paper. This helps determine the optimal partitioning based on the specific needs of model size, memory usage and communication requirements.

This table presents the calculation formula for tparam (time cost of all-gather for parameters) under three different partitioning granularities: no partitioning (N), intra-group partitioning (I), and global partitioning (G). It shows how the time cost changes depending on the number of GPUs in a group (m), the total number of GPUs (n), the bandwidth between GPUs within a group (B’), the bandwidth between groups (B), and the number of parameters (Ψ).

This table shows the calculation formula of the time cost (tgradient) for gradient synchronization during the backward pass in different model state partitioning strategies (No partitioning (N), Intra-group partitioning (I), and Global partitioning (G)). The formula considers the number of parameters (Ψ’), the number of GPUs in a group (m), the total number of GPUs (n), inter-group bandwidth (B), and intra-group bandwidth (B’).

This table details the calculation formulas for the time cost of synchronizing gradients (tsyncg) in various partitioning strategies for the optimizer states. The formulas account for the number of parameters (Ψ’), the number of GPUs (n), the number of GPUs per group (m), the number of groups (g), inter-group bandwidth (B), and intra-group bandwidth (B’).

This table presents the calculation formulas for the time cost (tsyncp) of synchronizing model parameters after they have been updated, considering different partitioning strategies (no partitioning (N), intra-group partitioning (I), and global partitioning (G)) for parameters (p) and optimizer states (os). The formulas account for the number of trainable parameters (Ψ’), the number of GPUs in a group (m), the total number of GPUs (n), the number of groups (g = n/m), intra-group bandwidth (B’), and global bandwidth (B). The time cost is 0 when neither parameters nor optimizer states are partitioned.
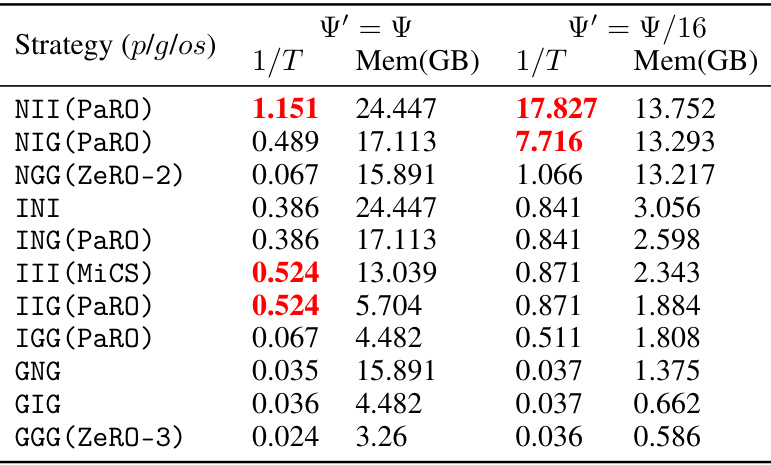
This table presents the results of training throughput (1/T) and GPU memory usage for the LLaMA-7B model under two different scenarios: full-parameter training (Ψ’ = Ψ) and partial-parameter training (Ψ’ = Ψ/16). For each scenario, it shows the performance of various PaRO-DP strategies along with some existing strategies like ZeRO-2 and ZeRO-3 for comparison. The results are intended to demonstrate the effectiveness of PaRO-DP strategies in optimizing the trade-off between training speed and memory consumption.

This table presents the results of training throughput (1/T) and GPU memory usage for the LLaMA-7B model under two different scenarios: full-parameter training (Ψ’=Ψ) and partial-parameter training (Ψ’=Ψ/16). It compares the performance of various PaRO-DP strategies against existing methods such as ZeRO-2, ZeRO-3, MiCS, and FSDP-hz. The 1/T values represent the training speed, while Mem(GB) shows the GPU memory consumption for each strategy.

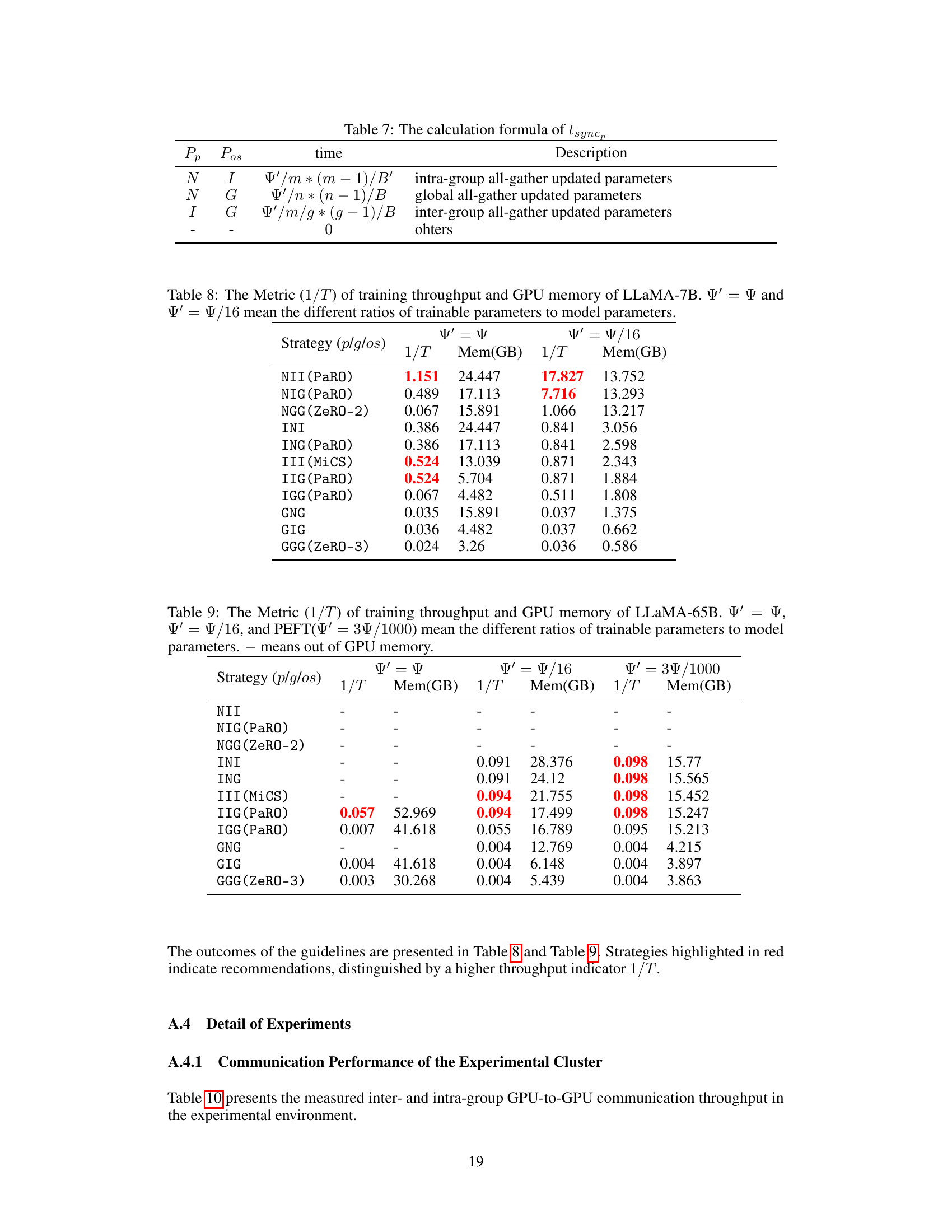
This table presents the measured inter- and intra-group GPU-to-GPU communication throughput in the experimental environment. It shows the transfer size (in bytes) and duration (in milliseconds) for both intra-node and inter-node communication and calculates the throughput in Gigabits per second (Gbps). This highlights the significant performance difference between communication within a single node and communication between nodes.

This table presents a comparison of different training strategies (including PaRO-DP strategies and other state-of-the-art methods) in terms of throughput and peak memory usage when training large language models with full trainable parameters. It showcases the superior performance of several PaRO-DP strategies compared to existing approaches under the same experimental setup.

This table presents the results of experiments conducted on 7B and 65B LLaMA models under partial-parameters training conditions (Ψ’=Ψ/16). It compares various strategies including PaRO-DP, ZeRO++, and FSDP-hz, evaluating their throughput and peak memory usage. The configurations used for each strategy are detailed, allowing for reproducibility. The table shows that PaRO-DP strategies generally achieve higher throughput while maintaining comparable or lower peak memory compared to other methods.

This table presents the results of experiments conducted using Parameter-Efficient Fine-Tuning (PEFT) with a ratio of trainable parameters to model parameters (Ψ’/Ψ) set to 3/1000. It compares the throughput and peak memory usage of different strategies (GGG (ZeRO-3), ING (PaRO), and ZERO++) in training the LLaMA-65B model, showcasing the performance improvement achieved by PaRO in the PEFT setting.

This table compares the throughput of different strategies for training the LLaMA-7B model on 32 GPUs, when using a full-parameter training setup (Ψ′ = Ψ). It shows the throughput (in samples/sec) for three different configurations of micro-batch size (MBS), accumulation steps (AS), and effective batch size (EBS). The table highlights the impact of dynamic effective batch size on training efficiency.

This table compares the throughput of different training strategies (IIG (PaRO) and GGG (ZeRO-3)) for the LLaMA-65B model on 64 GPUs, while varying the effective batch size. The results show that the IIG strategy of PaRO significantly outperforms ZeRO-3 under most conditions.
Full paper#