↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Clinical trials often struggle to identify subgroups that respond differently to treatments. Traditional methods pre-define subgroups at the start, limiting flexibility and potentially missing key insights. This leads to inefficient use of resources and reduced statistical power, particularly concerning costly treatments. This is a critical issue, as precision medicine demands identifying optimal treatments for specific patient populations.
This research introduces a new adaptive experimental strategy: dynamic subgroup identification with covariate-adjusted response-adaptive randomization (CARA). This innovative CARA design dynamically identifies the best subgroups during the trial, adjusting treatment allocation accordingly. It efficiently handles ties between subgroups and boasts a higher probability of correctly identifying the best subgroup(s) than conventional methods. Theoretical results confirm the statistical validity and efficiency of the proposed method, while simulations and a real-world case study demonstrate its practical utility.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel statistical design for dynamic subgroup identification in clinical trials. This addresses the limitations of traditional designs which pre-define subgroups, leading to inefficient use of resources and reduced statistical power. The design’s adaptability and efficiency are particularly valuable when dealing with expensive treatments and limited patient populations, making it highly relevant to precision medicine research.
Visual Insights#
This figure compares the performance of the proposed dynamic subgroup identification strategy with three other methods: complete randomization, epsilon-greedy, and upper confidence bound 1. The y-axis represents the probability of correctly identifying the best subgroups, and the x-axis represents the experimental stage. The proposed method consistently shows a higher probability of correct identification across all stages, demonstrating its superior performance compared to the conventional methods.

This table compares the performance of the proposed dynamic subgroup identification CARA design with three other conventional methods: complete randomization, epsilon-greedy, and UCB1. The comparison is based on four metrics: the estimated best subgroup treatment effect, its 95% confidence interval, the square root of N-scaled bias, and the standard deviation. The results show that the proposed method achieves a smaller standard deviation and √N-scaled bias, indicating higher efficiency and less bias, while maintaining comparable treatment effect estimates.
In-depth insights#
Adaptive Trial Design#
Adaptive trial designs represent a significant advancement in clinical research, offering the potential to optimize trials in real-time. The core principle is to modify aspects of the trial based on accumulating data, thus increasing efficiency and potentially improving patient outcomes. This might involve adjusting sample size, treatment allocation probabilities (e.g., response-adaptive randomization), or even the inclusion/exclusion criteria for participants. A key advantage is the ability to detect treatment effects sooner than traditional fixed-sample designs, potentially leading to earlier termination if a treatment proves overwhelmingly superior or inferior. However, careful consideration is crucial. Adaptive designs introduce complexities in statistical analysis, requiring specialized methods to account for the data-dependent nature of the trial. Furthermore, ethical considerations must be carefully addressed to ensure that adaptations do not unduly favor one treatment arm or compromise patient safety. Ultimately, adaptive designs offer a powerful tool for streamlining clinical trials, but their successful implementation demands meticulous planning and rigorous statistical validation.
CARA Algorithm#
A CARA (Covariate-Adjusted Response-Adaptive) algorithm, in the context of clinical trials, dynamically allocates treatments to participants based on observed outcomes and covariates. Its adaptive nature is crucial, allowing for adjustments during the trial itself, unlike traditional fixed-design approaches. This adaptability potentially leads to more efficient use of resources by focusing on the most promising subgroups. The algorithm’s core strength lies in its ability to identify the best-performing subgroups dynamically. This implies it can uncover subgroups where treatment is most effective, even if those subgroups were not pre-defined. Efficient handling of ties between subgroups is also critical, as it ensures optimal allocation of resources. However, the computational cost of a CARA algorithm could be significant, and the method’s success depends heavily on assumptions about data distributions and the presence of confounders. Statistical validity and inference for the best subgroup treatment effect are key concerns which must be rigorously addressed.
Subgroup Inference#
Subgroup inference in clinical trials aims to identify patient subgroups that respond differently to treatments. This involves moving beyond simple averages and delving into the heterogeneity of treatment effects. Statistical methods are crucial for detecting these subgroups reliably, and challenges include handling multiple comparisons, controlling for confounding factors, and ensuring sufficient statistical power to detect true effects within smaller subgroups. Adaptive designs can offer efficiency gains, and causal inference techniques are invaluable to distinguish true treatment effects from spurious associations within subgroups. Validating subgroup findings through external datasets is critical to improve the generalizability and robustness of these insights in clinical practice. Ethical considerations must also be integrated, ensuring that trial design and analysis do not lead to inappropriate resource allocation or the exclusion of patients from potentially beneficial treatments.
Limitations & Future#
A thoughtful limitations and future work section should acknowledge the study’s methodological constraints, such as assumptions made, limited generalizability due to specific datasets used, and reliance on certain statistical techniques. It should also discuss potential biases and their impact on the results. Regarding future work, expanding the scope of the research by testing on a more diverse range of datasets, incorporating additional variables to explore the nuances of the phenomena under study, and developing improved methodological approaches to address limitations, are all promising directions. Validation studies with larger, independent data sets to verify robustness would strengthen the findings. Additionally, exploring the practical implications of the research through simulations or real-world applications would add further value. Finally, investigating potential ethical considerations and biases in the data or analysis is crucial for responsible research dissemination.
Statistical Validity#
Statistical validity, in the context of a research paper, centers on whether the statistical methods used appropriately address the research question and whether the conclusions drawn are supported by the data. It involves examining the study design, data collection techniques, and analytical choices. A statistically valid study employs methods that are powerful enough to detect true effects, while minimizing the chances of false positives or negatives. Careful attention to sample size, the choice of statistical tests, and the handling of potential confounding factors are crucial for ensuring statistical validity. Issues such as missing data, violations of assumptions underlying statistical tests, and the potential for multiple comparisons can all undermine statistical validity and must be thoughtfully addressed. The correct interpretation and reporting of statistical results are also integral to statistical validity; this requires an accurate reflection of the uncertainty inherent in statistical inferences, using appropriate measures of effect size and statistical significance.
More visual insights#
More on figures
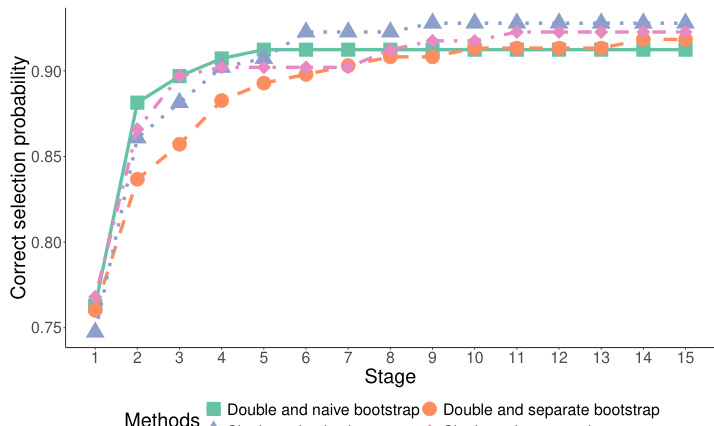
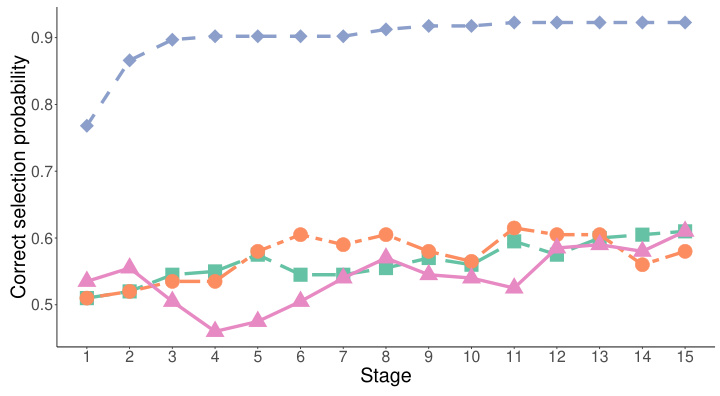
This figure compares the performance of four variations of the proposed dynamic subgroup identification strategy across 15 experimental stages. The variations differ in the methods used for selecting hyperparameters and merging subgroups. The y-axis represents the correct selection probability, indicating the success rate of correctly identifying the best subgroups. The x-axis shows the experimental stage. The lines represent the four variations: double and naïve bootstrap, single and naïve bootstrap, double and separate bootstrap, and single and separate bootstrap. The figure demonstrates how the correct selection probability evolves over time for each variation, showing the effectiveness of the proposed designs in identifying the best subgroups.
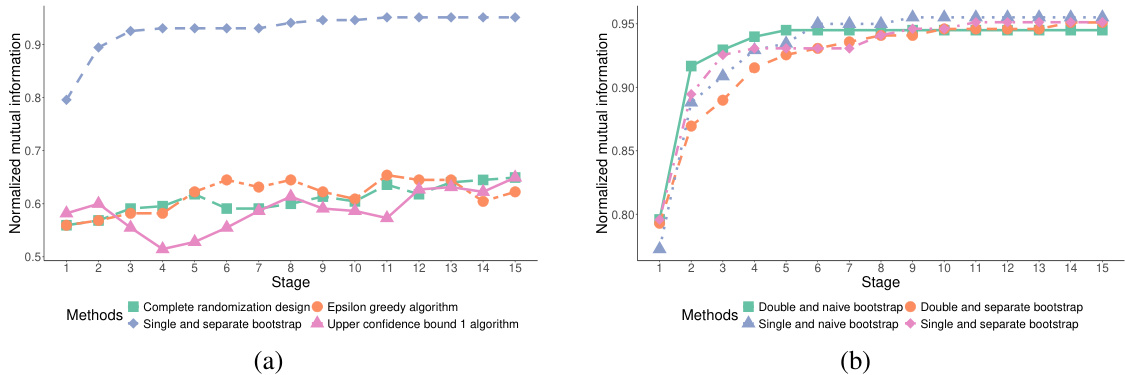
This figure compares the performance of the proposed dynamic subgroup identification strategy with three other methods: complete randomization, epsilon-greedy, and upper confidence bound 1. The y-axis represents the correct selection probability, and the x-axis represents the stage of the experiment. The proposed strategy consistently outperforms other methods across all stages, demonstrating its effectiveness in identifying the best subgroups.
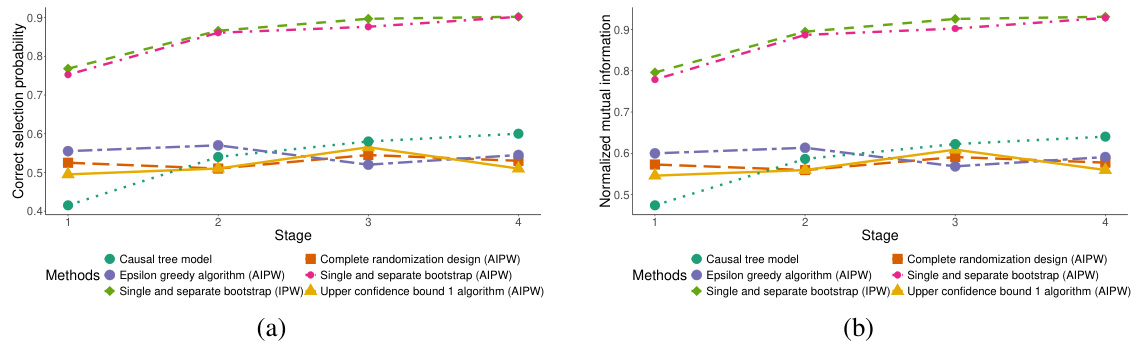
This figure compares the performance of several methods for identifying subgroups with the best treatment effects. The methods compared include the proposed dynamic subgroup identification strategy using both Inverse Probability Weighting (IPW) and Augmented Inverse Probability Weighting (AIPW) estimators, three conventional methods (complete randomization, epsilon-greedy, and upper confidence bound algorithms), and a causal tree model. The comparison is based on two metrics: correct selection probability and normalized mutual information. The results demonstrate that the proposed design strategy using AIPW and IPW consistently outperforms the conventional methods in terms of both metrics, especially at later stages.

This figure compares the performance of the proposed dynamic subgroup identification strategy with three other methods: complete randomization, epsilon-greedy algorithm, and upper confidence bound 1 algorithm. The y-axis represents the probability of correctly identifying the best subgroups, while the x-axis shows the experimental stage (indicating the number of participants enrolled). The results demonstrate that the proposed design strategy achieves a significantly higher probability of correct selection compared to the other three methods, and this probability increases as the number of stages progresses. The ‘single and separate bootstrap’ method refers to the authors’ proposed strategy.
More on tables

This table lists the notations used in the paper, categorized by symbols and descriptions. It includes symbols for experiment parameters (number of stages, number of participants, etc.), participant-level data (treatment assignment, observed outcome, covariates), subgroup-level data (sample size, proportions, treatment effects), and algorithm-specific variables (tie sets, estimated treatment effects). The table is essential for understanding the mathematical formalism and algorithm implementations described in the paper.
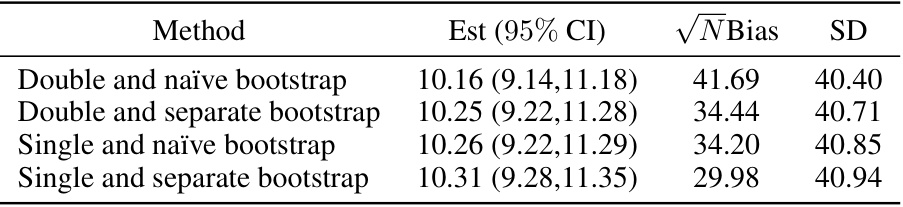
This table compares four variations of the proposed design strategy. The variations differ in the methods used for selecting hyperparameters and merging subgroups. The table shows the estimated best subgroup treatment effect, its 95% confidence interval, the √N-scaled bias, and the standard deviation for each variation. This allows for a comparison of the performance and accuracy of the different approaches.
Full paper#



















