↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world applications of online learning involve heavy-tailed loss distributions which violate common assumptions in multi-armed bandit (MAB) problems. Existing MAB algorithms often fail to provide strong performance guarantees under these conditions, lacking high-probability regret bounds, especially for the challenging best-of-both-worlds (BOBW) scenarios where the environment can be either adversarial or stochastic. This significantly limits their applicability to real-world scenarios.
This research introduces novel OMD-based algorithms that address these limitations. The key contribution lies in employing a log-barrier regularizer and relaxing the assumption of truncated non-negative losses. The proposed algorithms achieve near-optimal high-probability regret guarantees in adversarial scenarios and optimal logarithmic regret in stochastic scenarios. The results also extend to the challenging BOBW setting and achieve high-probability regret bounds with pure local differential privacy, improving upon existing approximate LDP results.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the limitations of existing multi-armed bandit algorithms which struggle with heavy-tailed losses (unbounded and potentially negative). By relaxing strong assumptions and providing high-probability regret bounds (both for adversarial and stochastic settings), it opens new avenues for research into real-world applications where data often violates standard assumptions. Furthermore, it presents the first high-probability best-of-both-worlds guarantees with pure local differential privacy, significantly advancing the field of private online learning.
Visual Insights#

The figure shows the decomposition of the regret in the adversarial regime before switching to Algorithm 1. The regret is broken down into three parts: Part A represents the regret incurred before the last round due to pulling suboptimal actions, while Part B is the regret from the last round and is bounded by twice the width of the confidence interval. Part C combines the remaining regret terms related to the best-fixed action in hindsight, also bounded using the width of the confidence interval. The equation is used to derive high-probability regret guarantees before the algorithm switches to handle the adversarial setting.
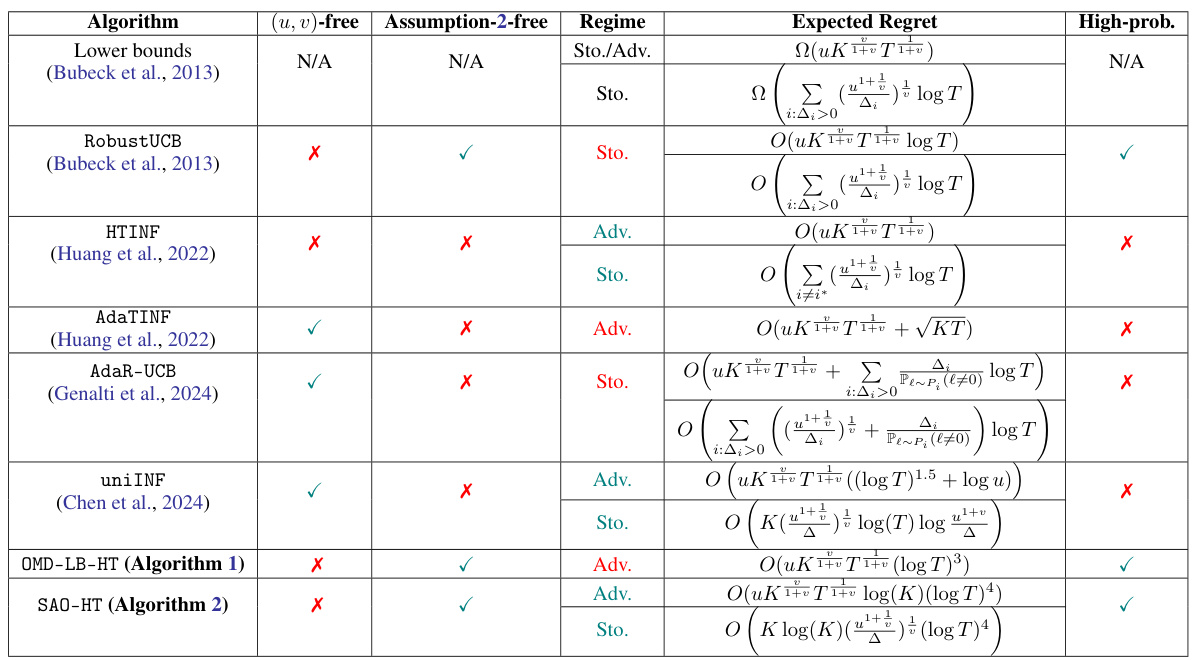
This table compares the proposed algorithm with related work on heavy-tailed multi-armed bandits (MABs). It shows whether each algorithm provides guarantees for unknown heavy-tail parameters (u, v), whether it relies on a strong assumption (Assumption 2), the type of regime it addresses (stochastic or adversarial), the expected regret it achieves, and whether these guarantees are high-probability bounds or just expected bounds.
Full paper#