Gaussian Process Bandits for Top-k Recommendations

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in online recommendation systems. It introduces novel, efficient algorithms for top-k recommendations that overcome limitations of existing methods, opening up new avenues for research and development in this rapidly evolving field. The theoretical analysis and empirical results provide strong evidence supporting the effectiveness of the proposed algorithms, making this a significant contribution.

Visual Insights

#

This figure shows examples of Father’s Day gift recommendations from the Etsy online marketplace. The items are displayed in a visually engaging layout rather than a simple list. This complex layout highlights the limitations of simple cascade models that assume users examine items sequentially and stop once they find something suitable. The figure argues that more realistic bandit feedback models are necessary to capture actual user behavior in the context of complex interfaces.

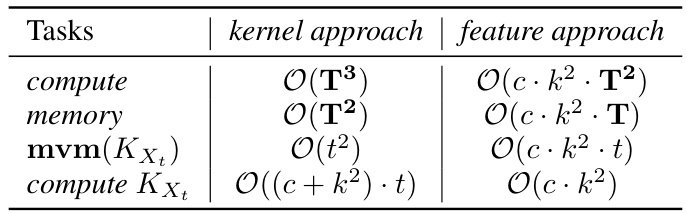
This table compares the computational and memory costs of two different approaches (kernel and feature) for the GP-TopK algorithm. It breaks down the costs into four tasks: total computation time and memory usage for T rounds, matrix-vector multiplication time, and kernel matrix update time. The table highlights the efficiency gains of the feature approach, especially as the number of rounds (T) increases.

In-depth insights

#

GP-Topk Algorithm

#

The GP-TopK algorithm presents a novel approach to top-k recommendation using Gaussian processes. Its core strength lies in handling full-bandit feedback, a challenging scenario where only a single scalar reward is received for the entire top-k set, unlike semi-bandit settings that provide individual item rewards. This avoids restrictive assumptions on the reward structure, making it more widely applicable. The algorithm leverages a Kendall kernel, specifically a novel weighted convolutional Kendall kernel, to model the reward function efficiently. This kernel addresses limitations of existing Kendall kernels, offering better expressiveness and scalability for top-k recommendations. Furthermore, efficient matrix-vector multiplication techniques are incorporated to reduce computational complexity. The theoretical analysis demonstrates sub-linear regret, and empirical results show superior performance compared to baselines across various scenarios, particularly in large arm spaces. However, the algorithm relies on local search for optimization, which might introduce a limitation in exploring the entire space. Therefore, future work might explore alternative optimization methods. Overall, GP-TopK offers a significant advancement in addressing the complexity of contextual top-k bandit problems.

Kendall Kernel

#

The research paper explores the use of Kendall kernels within Gaussian processes for top-k recommendation problems. Kendall kernels are crucial because they effectively capture the ordinal relationships between items in a ranking, unlike traditional kernels that only consider item-level features. The paper highlights the limitations of existing Kendall kernel variations for top-k scenarios, particularly their inability to handle scenarios where items are not present in all rankings being compared and their computational inefficiency. A novel weighted convolutional Kendall kernel is proposed to address these issues, combining the strengths of existing methods. This novel kernel offers increased flexibility by incorporating weights that allow for differential importance among rank positions and enhanced expressiveness by considering all items, not just those present in the intersection of top-k rankings. The paper demonstrates that this new kernel, along with efficient algorithms for matrix-vector multiplication using feature representations, leads to significant computational gains. Theoretical analysis shows sub-linear regret, a key metric in bandit algorithms, further supporting the effectiveness of the proposed approach.

Regret Analysis

#

Regret analysis in online learning algorithms, particularly in the context of top-k recommendation systems, is crucial for evaluating performance. It quantifies the difference between the rewards obtained by an algorithm and the rewards achievable by an optimal strategy with perfect knowledge. The paper focuses on bounding the cumulative regret, which is the sum of regrets over all rounds. The authors leverage Gaussian Processes and sophisticated kernel functions designed specifically for handling ranked lists (Kendall kernels) to model the reward function. This approach allows them to avoid restrictive assumptions about the reward structure or feedback mechanisms often found in simpler bandit settings, thus making their algorithm more robust and broadly applicable. The theoretical analysis establishes sub-linear regret bounds, confirming the algorithm’s efficiency. This theoretical work is further supported and validated by experiments, illustrating the practical benefits of their approach and comparing its performance against traditional baselines. The rigorous mathematical framework and the experimental evaluations work together to demonstrate the effectiveness of the proposed algorithm in a challenging combinatorial optimization problem. The regret bounds, while providing theoretical guarantees, also highlight the impact of factors such as the number of items, context dimensionality and the number of recommendations requested (k) on overall performance.

Empirical Results

#

An Empirical Results section in a research paper should thoroughly evaluate the proposed methodology. It needs to present a clear comparison against established baselines, demonstrating significant improvements where applicable. The datasets used should be well-described, allowing for reproducibility. A strong section will showcase results across multiple metrics and varying experimental conditions, not just focusing on a single, potentially cherry-picked scenario. Robust error bars or statistical significance measures are crucial for demonstrating the reliability of findings. It should be transparent about any limitations or confounding factors influencing the results. Ultimately, this section must provide compelling evidence to support the paper’s claims, clearly illustrating the practical effectiveness and generalizability of the proposed approach.

Future Works

#

The ‘Future Works’ section of this research paper presents exciting avenues for extending the GP-TopK algorithm. Improving computational efficiency remains paramount, especially for handling extremely large item catalogs. This could involve exploring more sophisticated kernel approximation techniques or investigating alternative optimization algorithms beyond local search. Further research could focus on developing more expressive kernels for top-k rankings, potentially by adapting kernels designed for other structured data, and formally analyzing their properties. The current regret bounds are asymptotic; empirical studies comparing the GP-TopK algorithm with state-of-the-art methods on a wider variety of real-world datasets would strengthen the findings. Finally, extending the algorithm to handle different types of feedback (e.g., implicit feedback, delayed feedback) would enhance its applicability and practical impact. Investigating the impact of bias in training data and methods to mitigate such bias would be crucial for responsible deployment.

More visual insights

#

More on figures

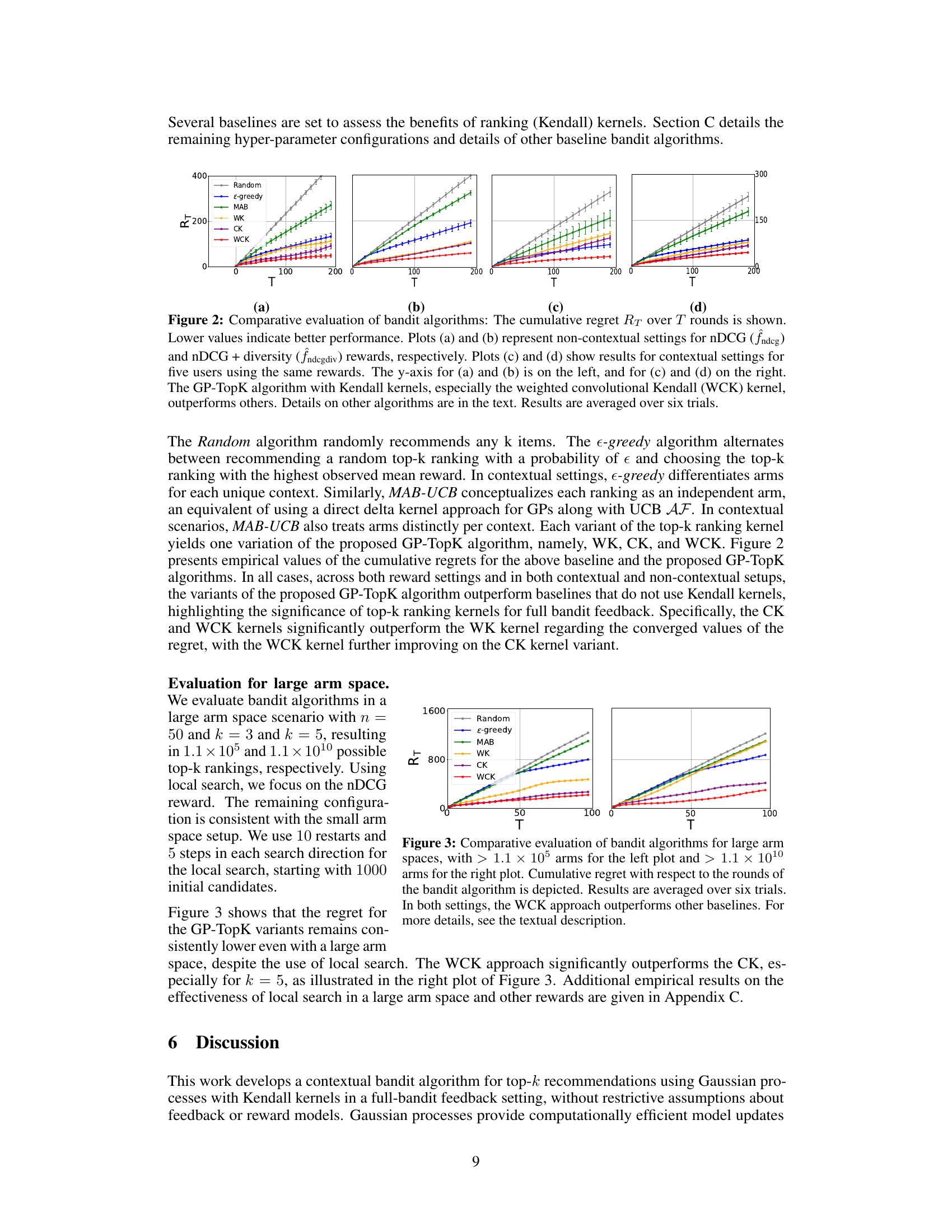
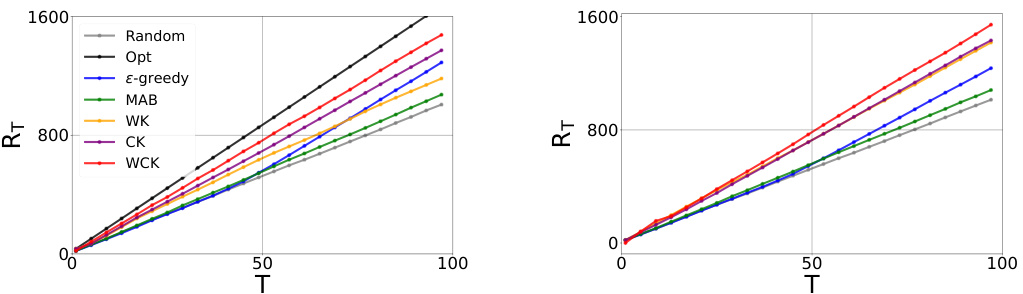
This figure compares the cumulative regret of several bandit algorithms across different settings. The algorithms are evaluated on two reward functions (nDCG and nDCG + diversity) and in both contextual and non-contextual scenarios. Lower regret indicates better performance. The results suggest that the GP-TopK algorithm with Kendall kernels, particularly the WCK kernel, significantly outperforms other baselines.

The figure compares the cumulative regret of different bandit algorithms across various settings. It shows the performance of the proposed GP-TopK algorithm against baselines (Random, ε-greedy, MAB) with and without contextual information and for different reward functions. Lower regret values indicate better performance.

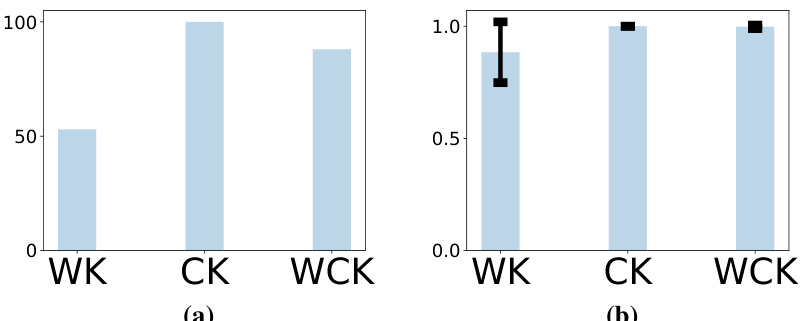
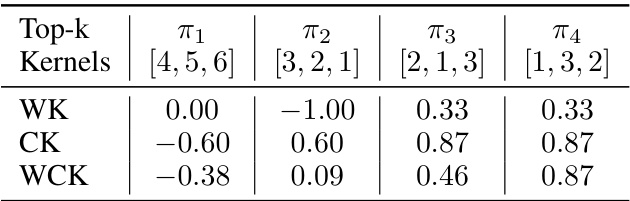
This figure shows the effectiveness of the local search algorithm used in the paper. The left plot shows the percentage of times (out of 100 trials) that the local search algorithm successfully found the optimal top-k ranking for the three different Kendall kernels: WK, CK, and WCK. The right plot shows the average objective value achieved by the local search algorithm across these 100 trials for each kernel. The results demonstrate that the local search algorithm is effective in finding high-quality solutions.

This figure compares the performance of several bandit algorithms (Random, e-greedy, MAB, WK, CK, WCK) in terms of cumulative regret (RT) over time (T). The algorithms are evaluated under different settings: (a) and (b) show non-contextual settings with nDCG and nDCG+diversity reward functions, while (c) and (d) show contextual settings (with five users) using the same reward functions. The figure demonstrates that the GP-TopK algorithm, especially when using the WCK kernel, outperforms the baselines.

More on tables

This table compares the computational and memory costs of two approaches (kernel and feature) for the GP-TopK algorithm across different tasks. The kernel approach uses full kernel matrices, while the feature approach leverages feature expansions for increased efficiency as the number of rounds (T) increases. The table highlights that the feature approach significantly reduces both computational and memory requirements, especially as T grows larger. The parameters c (context embedding size) and k (number of items) also influence these costs.

This table presents a comparison of computational and memory costs for two different approaches to the GP-TopK algorithm: the kernel approach and the feature approach. The rows detail the costs for the overall algorithm across T rounds, matrix-vector multiplication, and kernel matrix updates. The columns show the results for both the kernel (full kernel matrices) and feature (feature expansions) approaches. It highlights the efficiency gains of the feature approach for large T values.

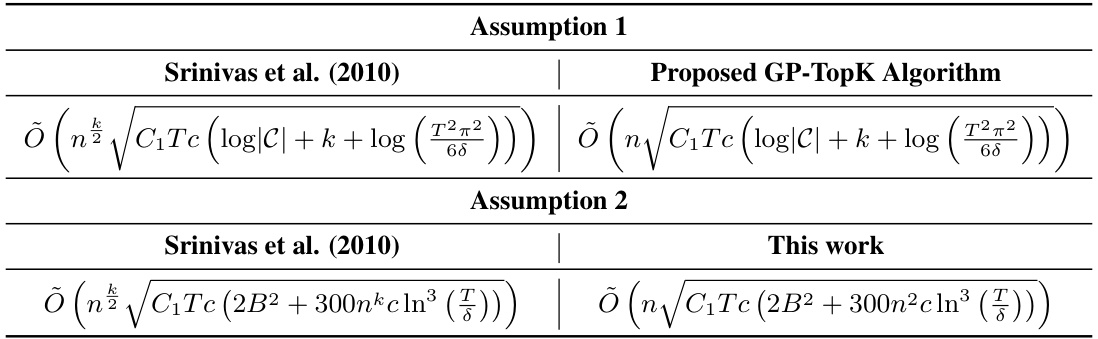
This table compares the computational and memory costs of two different approaches for the GP-TopK algorithm: the kernel approach (using full kernel matrices) and the feature approach (using feature expansions). The costs are broken down into three parts: total compute and memory, time for matrix-vector multiplication, and time to update the kernel matrix. The table shows that the feature approach scales more efficiently with respect to the number of rounds (T) and the number of items (k).

This table compares the computational and memory complexities of two approaches (kernel and feature) for the GP-TopK algorithm across various tasks. It shows how these complexities scale with the number of rounds (T), the number of items (k), and the embedding size for contexts (c). The feature approach, a novel contribution of the paper, is shown to be significantly more efficient than the kernel approach, particularly for larger datasets and more rounds.

This table provides a detailed comparison of the computational and memory requirements for the proposed GP-TopK algorithm using two different approaches: a kernel approach and a novel feature approach. The analysis covers various aspects including total compute and memory, matrix-vector multiplication time, kernel matrix update time, and their dependence on different parameters like embedding size (c), number of items (k), and number of rounds (T).

Full paper

#