↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Large language models (LLMs) excel at image and video generation but suffer from the high computational cost of self-attention. The quadratic complexity of self-attention poses a significant challenge for generating high-resolution images and videos; it makes the process slow and expensive. This paper introduces DiTFastAttn, a post-training compression method designed to overcome these limitations.
DiTFastAttn identifies and addresses three key redundancies in the attention computation: spatial, temporal, and conditional redundancy. To mitigate these redundancies, three novel techniques are proposed: Window Attention with Residual Sharing, Attention Sharing across Timesteps, and Attention Sharing across CFG. When applied to state-of-the-art diffusion transformer models, DiTFastAttn shows significant improvements. It achieves a reduction of up to 76% in attention FLOPs and delivers a speedup of up to 1.8x for high-resolution image generation. The method also shows positive effects for video generation, indicating that it’s a versatile approach applicable to different LLMs and applications.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on diffusion models, particularly those focusing on efficiency and scalability. It directly addresses the computational bottleneck of self-attention in diffusion transformers, a significant hurdle in generating high-resolution images and videos. The proposed techniques offer a promising avenue for accelerating inference, enabling broader accessibility and wider adoption of these models. The findings are directly applicable to improving existing models and inspire future research into efficient transformer architectures.
Visual Insights#

This figure demonstrates the efficiency gains of DiTFastAttn on PixArt-Sigma for image generation at various resolutions. The left panel is a bar chart showing the fraction of FLOPs (floating-point operations) used by different components (raw attention, DiTFastAttn, and others) for various image resolutions (512x512, 1024x1024, 2048x2048). The right panel shows example image generation results comparing the original PixArt-Sigma model to the one enhanced with DiTFastAttn at 1024x1024 resolution. This visually demonstrates the improved efficiency without significant loss in quality.

This table presents the results of image generation experiments using DiTFastAttn on different models (DiT-XL-2 512x512, PixArt-Sigma-XL 1024x1024, PixArt-Sigma-XL 2048x2048) at varying compression ratios. It shows the FID (Fréchet Inception Distance), IS (Inception Score), and CLIP scores, which are common metrics for evaluating image quality. ‘Attn FLOPs’ indicates the percentage of FLOPs (floating-point operations) in the attention mechanism relative to the uncompressed model, demonstrating the computational savings achieved by the compression technique. The table allows comparison of the trade-off between compression level and generated image quality.
In-depth insights#
Attn Compression#
The concept of ‘Attn Compression’ in the context of large language models centers on reducing the computational cost associated with the self-attention mechanism, a core component of transformer architectures. Self-attention’s quadratic complexity with respect to sequence length makes processing long sequences computationally expensive. Attn Compression techniques aim to mitigate this by identifying and exploiting redundancies within the attention mechanism. This might involve focusing on local attention windows instead of global attention, sharing attention computations across similar inputs or time steps, or employing various pruning or quantization methods to reduce the number of parameters and computations. The ultimate goal is to improve the efficiency and scalability of transformer models, enabling them to handle longer sequences and higher resolutions with reduced computational resources and latency, thus broadening their applicability to more demanding tasks.
Redundancy Types#
The concept of ‘Redundancy Types’ in the context of diffusion transformer models is crucial for optimizing computational efficiency. The authors likely identify several key areas where redundancy occurs: Spatial redundancy, arising from many attention heads focusing on local information rather than processing the entire image; Temporal redundancy, where similar attention patterns emerge across consecutive denoising steps, leading to duplicated computations; and Conditional redundancy, where similarities exist between the attention mechanisms used for conditional and unconditional image generation. Understanding and addressing these redundancies is essential to creating more efficient and scalable diffusion models, especially at high resolutions. By targeting these specific areas of redundancy, the authors aim to develop compression techniques that minimize the computational overhead without compromising the quality of generated images.
WA-RS Method#
The WA-RS (Window Attention with Residual Sharing) method cleverly addresses the spatial redundancy inherent in self-attention mechanisms within diffusion transformer models. It leverages the observation that many attention heads focus primarily on local spatial information, with attention values diminishing for distant tokens. Instead of solely employing window attention, which can lead to performance degradation, WA-RS caches the residual difference between the output of full attention and window attention at a given step. This residual, representing the information lost by using a window, is then added to the window attention output in subsequent steps. This ingenious technique effectively retains long-range dependencies while significantly reducing computational cost by only focusing on the necessary computations within the window. The key insight lies in exploiting the high similarity between residuals across consecutive steps, enabling this training-free method to effectively compress attention computations without retraining the model and maintain model performance.
AST & ASC#
The proposed methods, AST (Attention Sharing across Timesteps) and ASC (Attention Sharing across CFG), target temporal and conditional redundancies in diffusion models. AST leverages the similarity between attention outputs of consecutive timesteps, reducing computation by reusing earlier step’s results where similarity is high. This is a significant optimization as diffusion models involve many iterative denoising steps. ASC exploits the similarity between conditional and unconditional attention outputs in classifier-free guidance (CFG). By sharing attention outputs between these two inference paths, redundant calculations are avoided, especially in cases where the conditional and unconditional outputs exhibit high similarity. Both AST and ASC are training-free post-processing methods, making them easily applicable to pre-trained diffusion models. Their effectiveness relies on the presence of temporal and conditional redundancies, which should be carefully assessed for different model architectures and task settings. The combination of AST and ASC with other compression methods, as shown in the paper, demonstrates potential synergy, further improving efficiency.
Future Works#
Future work could explore several promising avenues. Extending DiTFastAttn to other diffusion models beyond the ones evaluated is crucial to establish its general applicability and effectiveness. Investigating more sophisticated redundancy detection methods could further refine the compression strategy, leading to even greater performance gains. Adaptive techniques that dynamically adjust the compression level based on the input or generation stage could optimize the balance between speed and quality. A deeper investigation into the interaction between DiTFastAttn and different sampling methods would be valuable to understand its effects on both speed and image/video quality. Finally, research into combining DiTFastAttn with other compression techniques such as quantization or pruning might yield synergistic improvements, creating even more efficient and effective diffusion models.
More visual insights#
More on figures
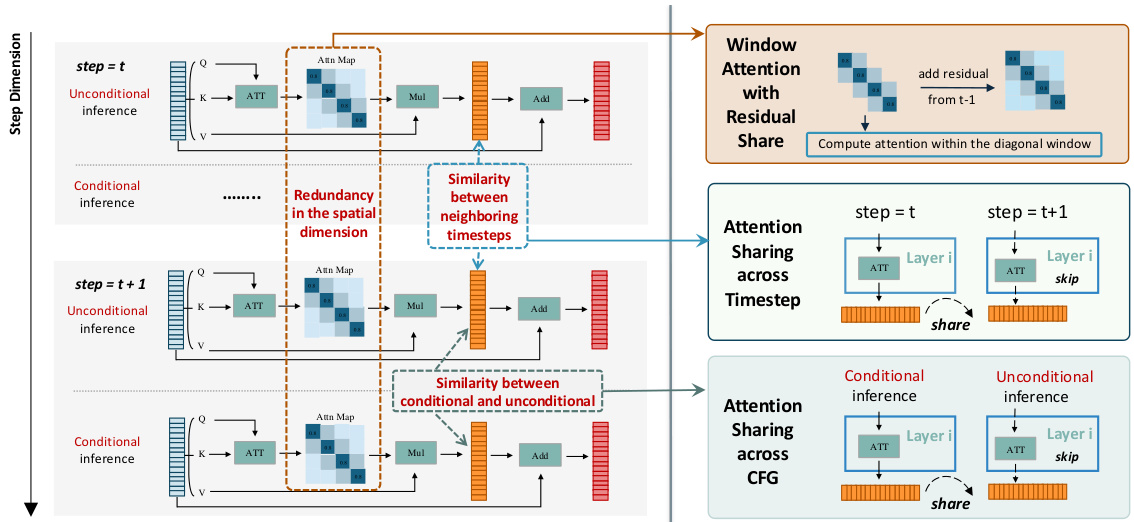
This figure illustrates the three types of redundancies identified in the attention computation of Diffusion Transformers (DiT) during inference: spatial redundancy, temporal redundancy, and conditional redundancy. For each type of redundancy, the figure shows the corresponding compression technique used in DiTFastAttn to reduce computational cost. These techniques include Window Attention with Residual Sharing (WA-RS) to reduce spatial redundancy, Attention Sharing across Timesteps (AST) to reduce temporal redundancy, and Attention Sharing across CFG (ASC) to reduce conditional redundancy. The figure visually represents how these techniques are integrated to improve efficiency.

This figure illustrates the concept of Window Attention with Residual Sharing (WA-RS). Part (a) shows that the attention values concentrate in a window along the diagonal of the attention matrix, and that the error (Mean Squared Error, MSE) between the full attention and the window attention outputs is minimal and relatively consistent across steps. Part (b) illustrates the WA-RS technique which takes advantage of this consistency by caching the residual (difference between full and window attention) and reusing it for subsequent steps, saving computation while maintaining accuracy.
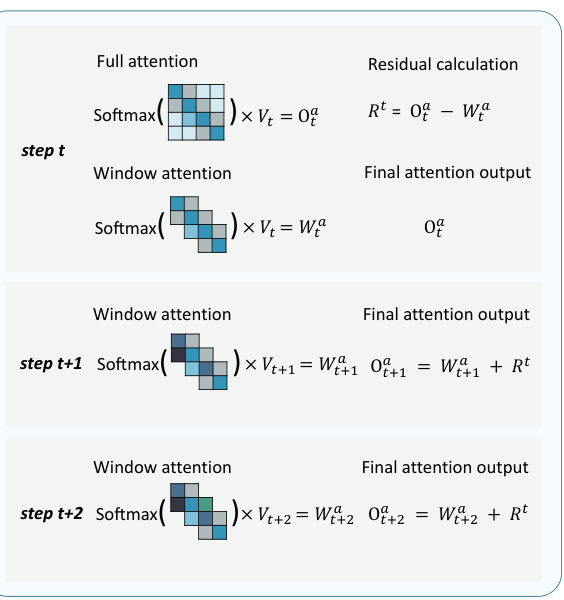
This figure illustrates the core concept of Window Attention with Residual Sharing (WA-RS). The left panel (a) shows that attention values concentrate in a diagonal window. It also demonstrates that the mean squared error (MSE) between consecutive steps’ attention output is significantly higher than the MSE between consecutive steps’ residuals (the difference between full attention and window attention). The right panel (b) details the WA-RS mechanism. It shows how a residual from the previous step is cached and reused in subsequent steps, saving computation and improving the accuracy of window attention.
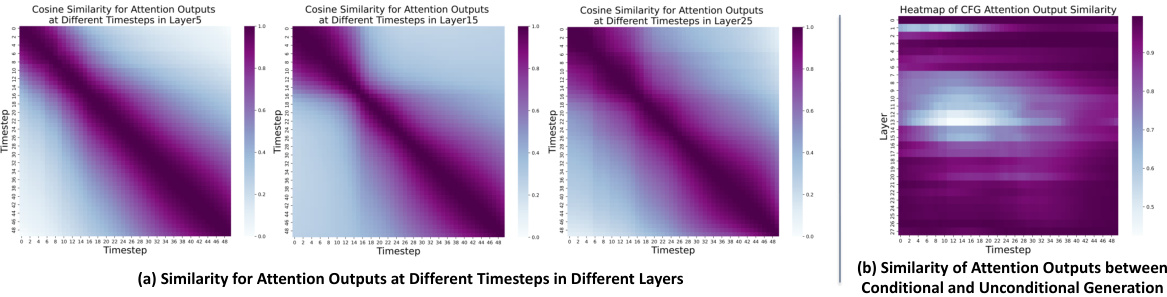
This figure visualizes the similarity of attention outputs in a diffusion transformer model across different steps (time) and between conditional and unconditional inference. Panel (a) shows heatmaps representing the cosine similarity between attention outputs of the same attention head at consecutive time steps for three different layers (5, 15, and 25). Warmer colors (purple) indicate higher similarity. Panel (b) shows a heatmap illustrating the cosine similarity between conditional and unconditional attention outputs across different time steps for various layers. This demonstrates the redundancy that can be exploited by the proposed DiTFastAttn method.
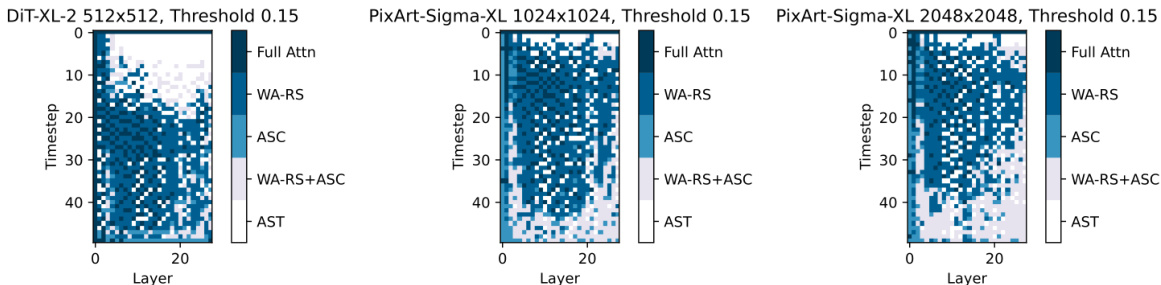
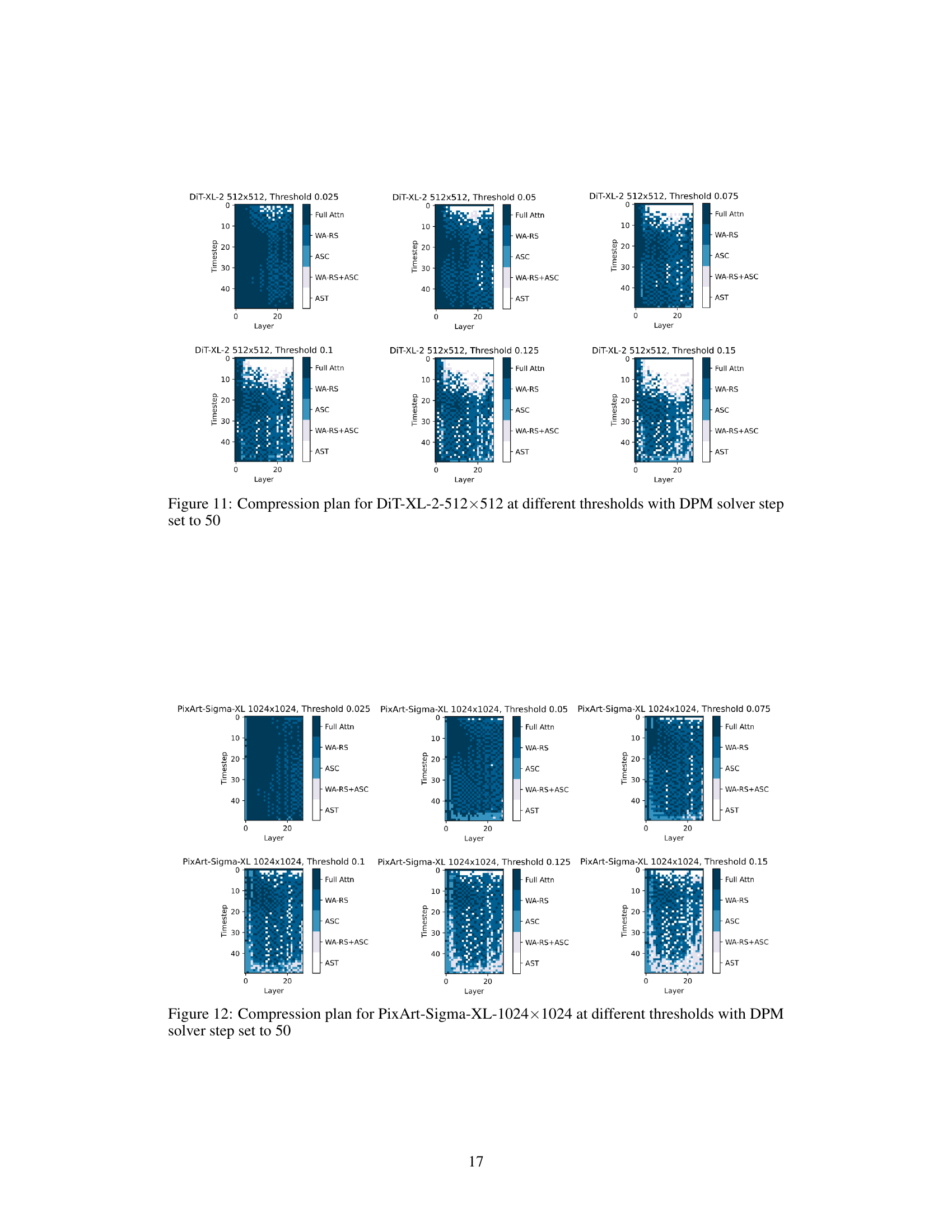
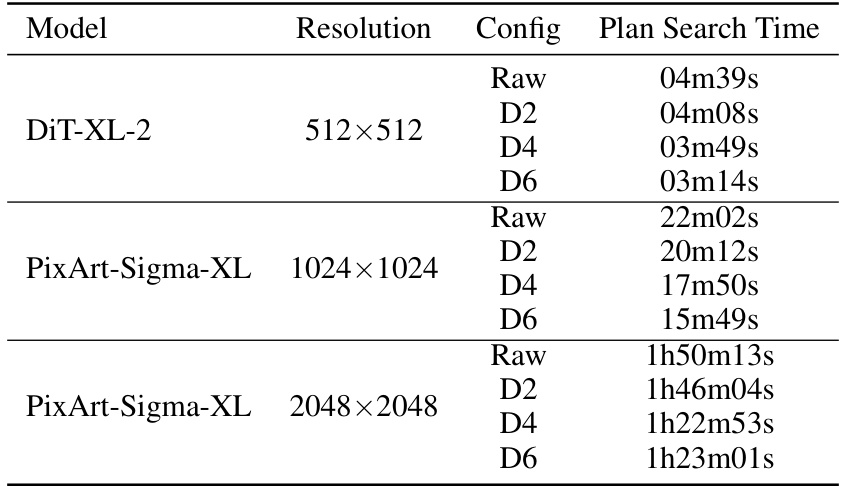
This figure shows the compression plan obtained by applying the proposed greedy search method to three different models (DiT-XL-512, PixArt-Sigma-XL-1024, and PixArt-Sigma-XL-2048) at a threshold of 0.15 (D6). The heatmaps illustrate which compression strategy (full attention, WA-RS, ASC, WA-RS+ASC, or AST) is applied to each layer at each timestep during the diffusion process. The color intensity in each cell represents the selected compression strategy. It highlights the variability of the optimal compression strategies depending on the model architecture and resolution.

This figure displays image generation results from three different models (DiT-XL-2-512, PixArt-Sigma-1024, and PixArt-Sigma-2048) at various resolutions and compression ratios (D1 to D6). Each row represents a different model and resolution, with the leftmost column showing the original image (‘Raw’). Subsequent columns illustrate the generated images using DiTFastAttn with increasing compression levels (D1 to D6), which trade off between speed and image quality. The figure helps visualize the effect of DiTFastAttn’s different compression strategies on the generated image quality, showing how the models maintain image quality to different levels depending on the degree of compression used.

This figure shows image generation samples from the DiTFastAttn model at various resolutions and compression ratios. It visually demonstrates the impact of the proposed compression techniques on image quality at different levels of compression. The samples allow for a qualitative assessment of how well the method maintains image quality while reducing computational cost.

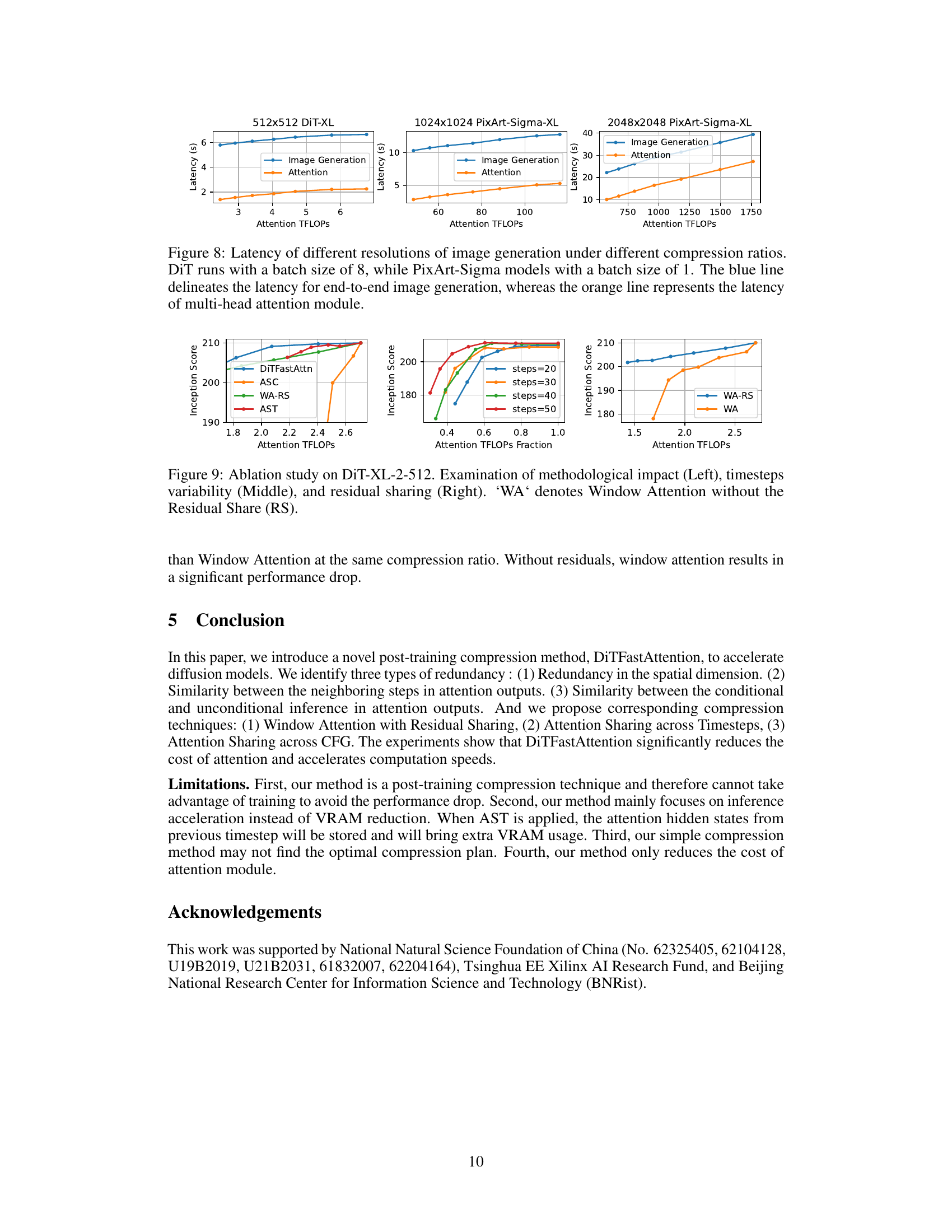
This figure shows the latency (time taken) for image generation and the attention mechanism separately, at different resolutions (512x512, 1024x1024, and 2048x2048) and various compression ratios. The x-axis represents the computational cost (TFLOPS) of the attention mechanism. The y-axis is the latency in seconds. Different batch sizes were used for DiT-XL (batch size 8) and PixArt-Sigma-XL (batch size 1). The blue line indicates the overall generation latency, while the orange line indicates the latency specifically for the attention part of the generation process. The figure demonstrates the impact of the proposed compression methods on the runtime of diffusion models.
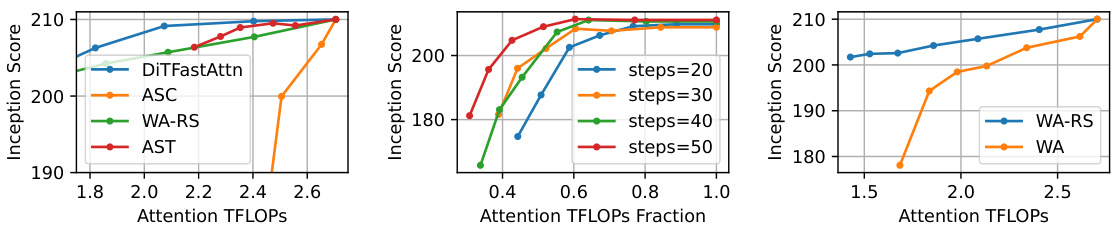
This figure presents an ablation study conducted on the DiT-XL-2-512 model to analyze the impact of different components of the proposed DiTFastAttn method. The left panel shows a comparison of DiTFastAttn against its individual components (ASC, WA-RS, and AST) in terms of Inception Score versus the attention FLOPs fraction. The middle panel demonstrates the impact of varying the number of denoising steps (20, 30, 40, and 50) on the Inception Score at different attention FLOPs fractions. The right panel specifically examines the contribution of the residual sharing technique within the Window Attention (WA-RS) method by contrasting its performance with a version without residual sharing (‘WA’) across different attention FLOP levels.

This figure demonstrates the efficiency gains of DiTFastAttn when generating images at different resolutions. The left panel shows a bar graph comparing the fraction of FLOPs (floating-point operations) used by DiTFastAttn versus the original PixArt-Sigma model at 512x512, 1024x1024, and 2048x2048 resolutions. The right panel presents qualitative image samples to illustrate the model’s output quality after applying DiTFastAttn on 1024x1024 images.
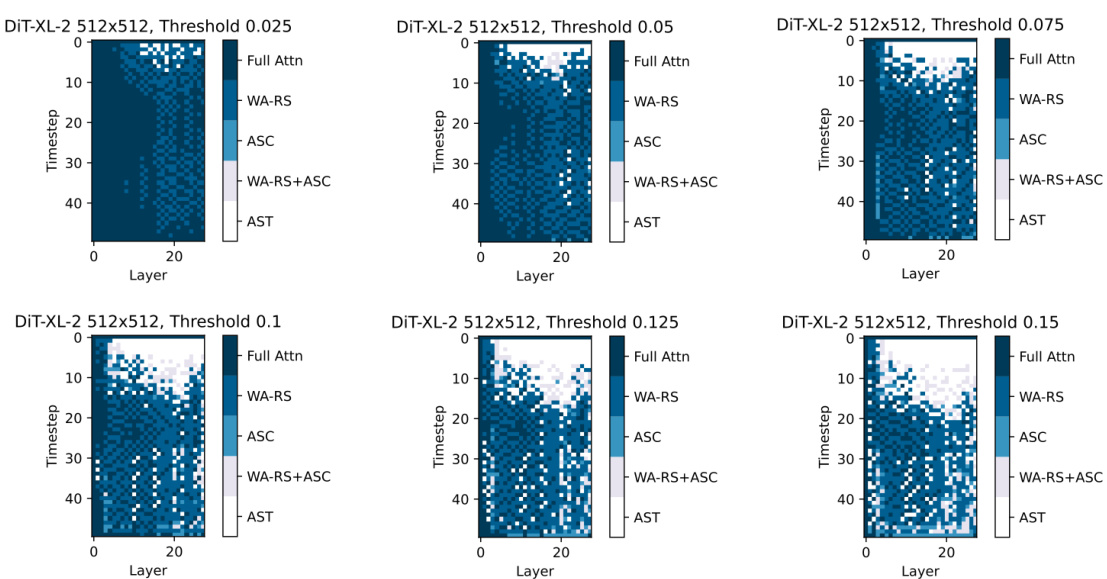
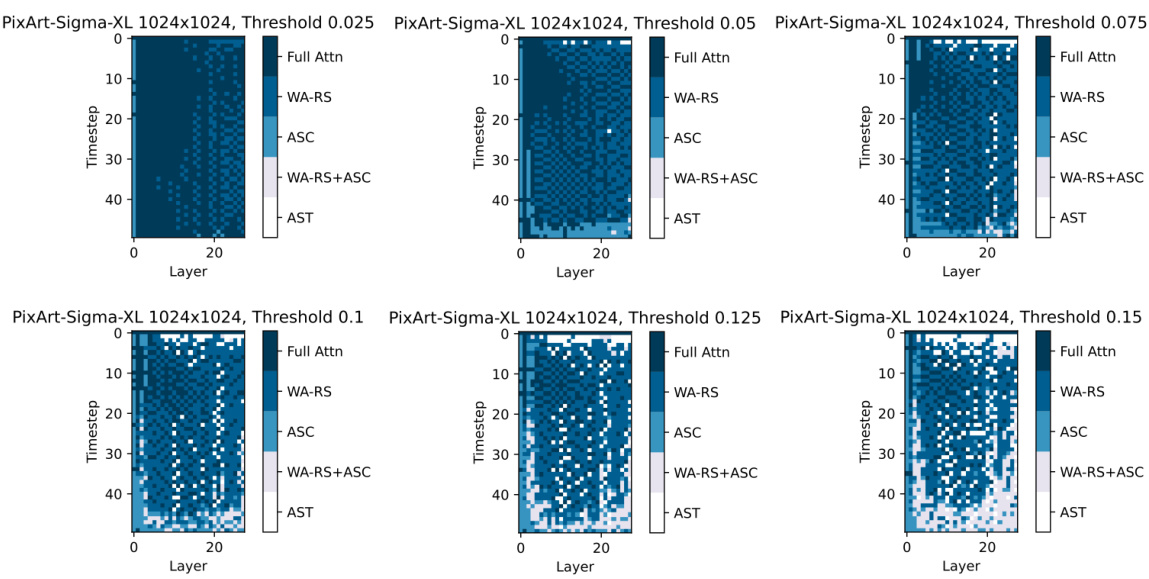
This figure displays the compression plans generated by the greedy search method for DiT-XL-2-512x512 model at six different thresholds (0.025, 0.05, 0.075, 0.1, 0.125, and 0.15). Each heatmap represents a compression plan for a specific threshold, visualizing the chosen compression strategy (Full Attn, WA-RS, ASC, WA-RS+ASC, AST) for each layer at each timestep. The color intensity likely represents the degree of compression applied. The figure shows how the choice of compression strategy varies across layers and timesteps depending on the chosen threshold, highlighting the adaptive nature of the proposed method.
This figure visualizes the compression strategies selected by the DiTFastAttn algorithm for three different diffusion transformer models (DiT-XL-512, PixArt-Sigma-XL-1024, and PixArt-Sigma-XL-2048) at a specific threshold (D6). Each heatmap represents the compression plan for a single model, showing which compression techniques (Full Attn, WA-RS, ASC, WA-RS+ASC, AST) were applied to each layer at each timestep during the denoising process. The color intensity in each cell indicates the strength of the applied compression technique. The results showcase that the optimal compression strategy varies across different models and image resolutions, highlighting the adaptive nature of the proposed method.
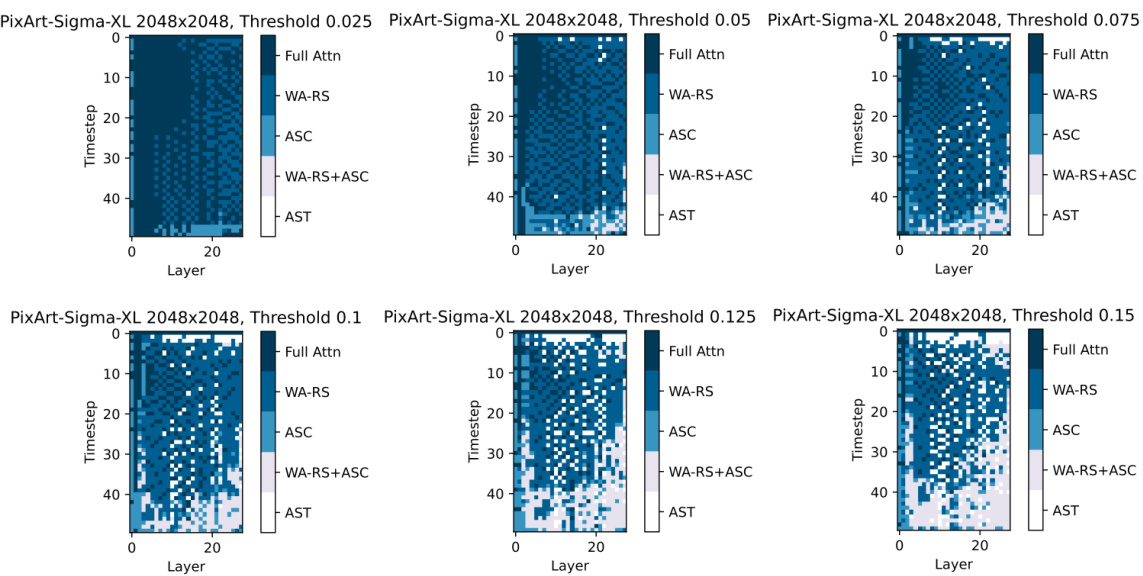
This figure visualizes the compression strategies applied to different layers and timesteps of three different diffusion transformer models (DiT-XL-512, PixArt-Sigma-XL-1024, and PixArt-Sigma-XL-2048) at threshold level D6 (δ=0.15). Each model uses a combination of techniques (WA-RS, AST, and ASC) to reduce computational costs, with the specific strategy applied depending on the layer and timestep. The color intensity represents the type of compression technique used, ranging from full attention to different combinations of WA-RS, AST, and ASC.

This figure shows the impact of negative prompts on image generation quality at different compression levels. The top half displays images generated without a negative prompt, while the bottom half shows images generated with the negative prompt ‘Low quality’. The three columns (D2, D4, D6) represent different compression ratios achieved by the DiTFastAttn algorithm, demonstrating how the algorithm’s compression affects image quality, especially when negative prompts are used.
More on tables

This table presents the results of image generation experiments using DiTFastAttn on three different models: DiT-XL-2 512x512, PixArt-Sigma-XL 1024x1024, and PixArt-Sigma-XL 2048x2048. For each model and resolution, it shows the performance metrics (IS, FID, CLIP) for the original model (Raw) and for six different compression levels (D1-D6). The ‘Attn FLOPs’ column indicates the percentage of attention FLOPs remaining after compression compared to the original model.
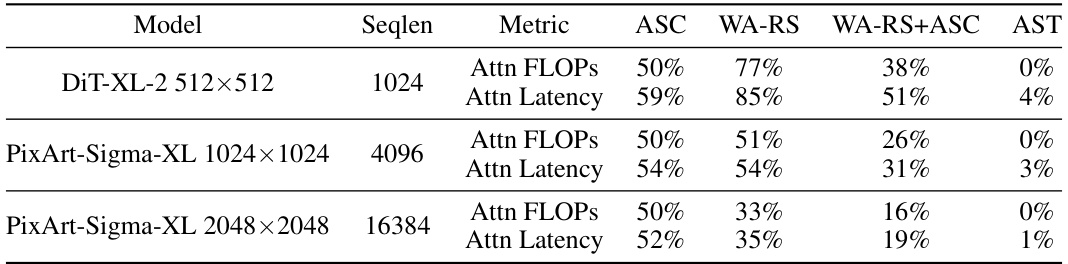
This table shows the results of applying DiTFastAttn to three different diffusion transformer models with different sequence lengths. It presents the fraction of FLOPs (floating-point operations) and latency reduction achieved by the DiTFastAttn method for each model. The FLOPs fraction represents the percentage reduction in attention computation compared to the original model, while the latency fraction indicates the percentage reduction in inference time. The results are broken down by the different compression techniques used in DiTFastAttn (ASC, WA-RS, WA-RS+ASC, and AST). The latency is measured using an Nvidia A100 GPU.
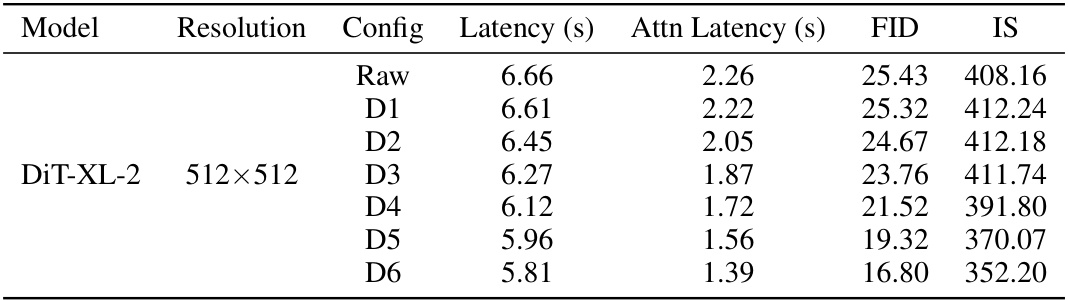
This table presents the results of image generation experiments using DiTFastAttn on three different models (DiT-XL-2 512x512, PixArt-Sigma-XL 1024x1024, and PixArt-Sigma-XL 2048x2048) at various compression ratios (D1-D6). For each model and compression ratio, the table shows the Inception Score (IS), Fréchet Inception Distance (FID), CLIP score, and the fraction of attention FLOPs relative to the original model. The FID and IS scores are metrics for image quality, while the CLIP score measures the similarity between generated images and text prompts, and the attention FLOPs indicate the computational savings achieved by DiTFastAttn.
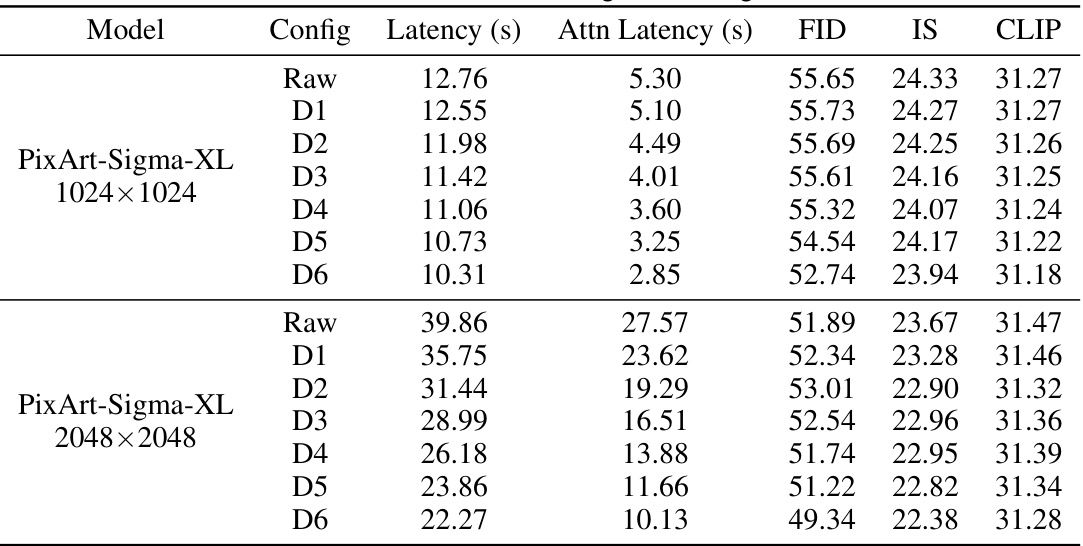
This table presents the results of image generation experiments using DiTFastAttn on three different models at various resolutions. It shows the FID, IS, and CLIP scores, as well as the fraction of attention FLOPs (floating-point operations) compared to the original, uncompressed models. Different compression ratios (D1-D6) are evaluated, showing the impact of the DiTFastAttn method on both performance and computational cost. The higher the resolution, the more significant the reduction in FLOPs and the potential for speedup.
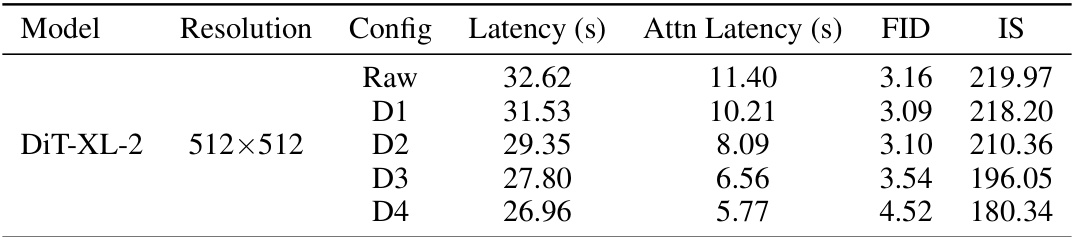
This table presents the results of image generation experiments using DiTFastAttn on three different models at various resolutions. It compares the raw model’s performance (no compression) to DiTFastAttn’s performance at different compression levels (D1-D6). The metrics used to evaluate performance are Inception Score (IS), Fréchet Inception Distance (FID), and CLIP score. The ‘Attn FLOPs’ column indicates the percentage of FLOPs (floating-point operations) related to attention in each configuration, relative to the raw model.
This table presents a comparison of the image generation performance of the DiTFastAttn model at different resolutions and compression ratios. It shows the FID, IS, and CLIP scores, which are metrics used to evaluate the quality of generated images. The table also indicates the fraction of FLOPs (floating-point operations) used for attention computation relative to the original model, reflecting the computational savings achieved through compression.
Full paper#