Provably Transformers Harness Multi-Concept Word Semantics for Efficient In-Context Learning

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in large language models (LLMs) and in-context learning (ICL). It provides a novel theoretical framework to understand how transformers leverage multi-concept word semantics for efficient ICL. The rigorous mathematical analysis and the demonstration of exponential convergence of 0-1 loss over highly non-convex training dynamics are significant contributions that advance our understanding of LLMs and their capabilities. Further research can leverage this foundation to develop more powerful LLMs and explore innovative ICL strategies.

Visual Insights

#

This figure illustrates the Idempotent Operator Techniques used in the paper’s analysis. It breaks down the complex interactions within the transformer model—specifically, the attention and MLP layers—into simpler, more manageable components. By employing idempotent decomposition, the analysis focuses on the evolution of key coefficients, thereby simplifying the study of the learning dynamics and ultimately, the convergence to the Bayes optimal test error.

In-depth insights

#

Multi-concept Semantics

#

The concept of “Multi-concept Semantics” in the context of transformer-based language models (LLMs) is crucial. It highlights the polysemous nature of words, meaning a single word can possess multiple meanings depending on context. LLMs must effectively manage and resolve these ambiguities to understand and generate natural language correctly. This is achieved by encoding words not as single, monolithic representations but as combinations of underlying concepts. These concepts are latent features, learned during model training, which are interwoven to form the final word embedding. The resulting semantic space exhibits geometric patterns: within-concept representations show positive correlations, indicating semantic similarity, while cross-concept vectors are near-orthogonal, representing distinct semantic categories. This multi-concept encoding enables LLMs to perform in-context learning effectively, generalizing to unseen tasks by leveraging the shared conceptual structure between known and novel scenarios. The success of in-context learning is directly tied to the ability of the model to extract and manipulate these interwoven concepts, highlighting the critical role that multi-concept semantics play in the overall functionality and performance of LLMs.

Transformer ICL

#

Transformer-based In-context Learning (ICL) is a fascinating area of research. The ability of large language models (LLMs) to solve new tasks with just a few examples, without explicit retraining, is remarkable. This paper delves into the theoretical underpinnings of this capability, focusing on how transformers leverage the multi-concept semantics of words. The core argument is that the geometric regularity of multi-concept word embeddings, specifically their positive inner products within concepts and near-orthogonality between concepts, underpins the effectiveness of ICL. This leads to exponential convergence of the 0-1 loss, showcasing the power of this approach beyond simple linear models. The analysis also touches upon the challenges of non-convex training dynamics, including softmax self-attention and ReLU-activated MLPs, offering valuable insights into the complex mechanisms driving ICL. Furthermore, this research directly addresses the strong out-of-distribution (OOD) generalization ability of transformers, a crucial aspect not fully explored by previous theoretical work. Overall, the paper provides a rigorous mathematical analysis that helps bridge the gap between empirical observations and theoretical understanding of ICL in transformers.

Exponential Convergence

#

The concept of “Exponential Convergence” in machine learning signifies a significant advancement over traditional linear or sublinear convergence rates. It implies that the learning process rapidly approaches its optimal solution, decreasing the error exponentially with each iteration. This is highly desirable, particularly in complex, high-dimensional settings like those encountered with deep learning models. The authors’ achievement of exponential convergence for a 0-1 loss in their transformer model is particularly noteworthy because of the inherent non-convexity associated with these models, making convergence significantly challenging. This result underscores the efficacy of the multi-concept semantic representation of words within their framework, which is integral to enabling powerful in-context learning. Such efficiency is crucial for the practical applicability of LLMs, especially when dealing with novel, unseen tasks. The demonstration of exponential convergence validates the effectiveness of their theoretical analysis and highlights the potential for developing even more efficient and robust LLMs.

OOD Generalization

#

The concept of “OOD Generalization” in the context of large language models (LLMs) signifies their ability to successfully handle tasks and data significantly different from those encountered during training (out-of-distribution). This capability is crucial for real-world applications where models often face unseen scenarios. The paper likely explores how LLMs’ internal representations and learning mechanisms enable such generalization. Multi-concept word semantics, where words possess multiple meanings encoded within the model, may play a crucial role in enabling this capability by allowing the LLM to flexibly adapt to new task contexts. The analysis might also reveal if certain geometric properties of the LLMs’ latent space facilitate successful OOD generalization. The theoretical analysis might demonstrate how such properties lead to efficient learning and near-optimal performance, even with limited training data from the novel tasks. Ultimately, understanding and improving OOD generalization is key for making LLMs truly robust and dependable systems for a broad range of applications.

Future Research

#

Future research directions stemming from this work could involve extending the theoretical analysis to more complex transformer architectures, such as those with multiple layers or different attention mechanisms. Investigating the impact of different loss functions beyond cross-entropy, and exploring alternative optimization algorithms could also yield valuable insights. A particularly promising area would be to empirically validate the theoretical findings on a wider range of tasks and datasets, potentially focusing on low-resource settings or out-of-distribution generalization scenarios. Finally, a deeper exploration of the connection between the geometric regularities observed in LLMs and their cognitive capabilities is warranted. This could involve exploring the relationship between the latent geometry and phenomena like concept intersection and reasoning.

More visual insights

#

More on figures

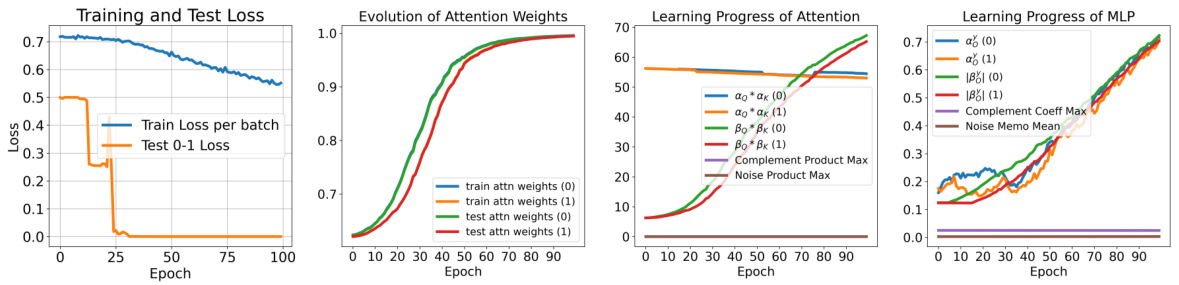
This figure presents the learning dynamics of the transformer model. The four subfigures show: (i) the training and test loss curves; (ii) the evolution of attention weights over time (correct attention weight, train and test); (iii) maximum values of different types of products (concept-specific, complement, noise), providing insights into the model’s learning of attention and concept representation; and (iv) evolution of MLP weights (correct attention weight, train and test). These subfigures jointly illustrate various aspects of the transformer’s learning progress, including the convergence of the model, the dynamics of attention weights, and the interplay of concept-specific semantics and noise during training.

This figure shows the learning dynamics of the transformer model under three different out-of-distribution (OOD) scenarios. The first two scenarios (a and b) investigate the impact of different prompt lengths during testing, while the latter two (c and d) explore the effects of altering the underlying data distribution (skewed concept distribution and switched semantic features). Each subfigure displays training and testing loss, evolution of attention weights, and learning progress of both attention and MLP layers over epochs, providing a comprehensive view of the model’s learning behavior in various OOD situations.

Full paper

#