↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Standard Gaussian Processes (GPs) struggle with real-world data containing non-Gaussian noise or outliers, leading to inaccurate predictions. Existing robust GP models often compromise accuracy or computational efficiency.
This work introduces Robust Gaussian Processes via Relevance Pursuit (RRP). RRP addresses this by using a sequential selection procedure that identifies and downweights outliers. This is achieved by learning data-point-specific noise levels while maximizing the log marginal likelihood, which surprisingly exhibits strong concavity. This concavity proves approximation guarantees, ensuring reliability and efficiency. Experiments show that RRP effectively handles various regression and Bayesian Optimization tasks, especially in challenging scenarios of sparse label corruptions.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel approach to robust Gaussian process regression that is both effective and efficient. It also provides theoretical guarantees for the proposed method, making it a significant contribution to the field. The research opens new avenues for further investigation in robust machine learning and Bayesian optimization.
Visual Insights#
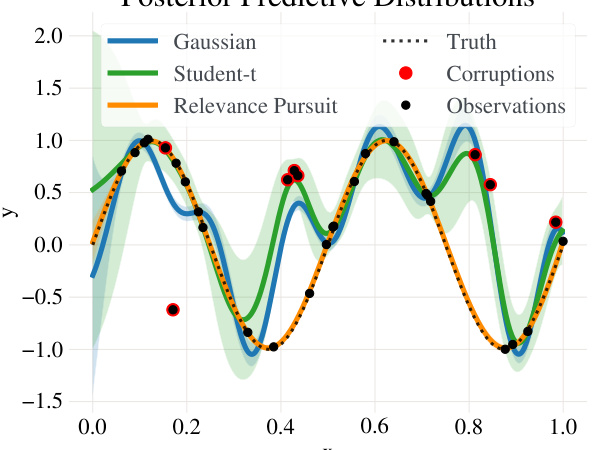
This figure compares the performance of three different Gaussian Process (GP) models on a regression task with label corruptions. The standard GP and a variational GP with a Student-t likelihood are shown to be negatively affected by the corrupted data points, while the proposed Robust Gaussian Processes via Relevance Pursuit (RRP) method accurately identifies and accounts for these corruptions, resulting in a significantly improved fit to the true underlying function.
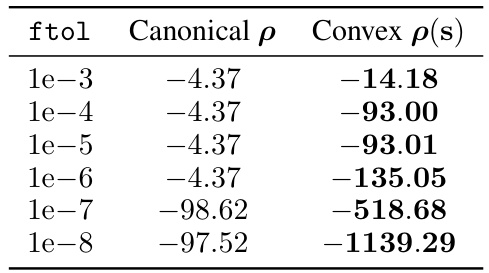
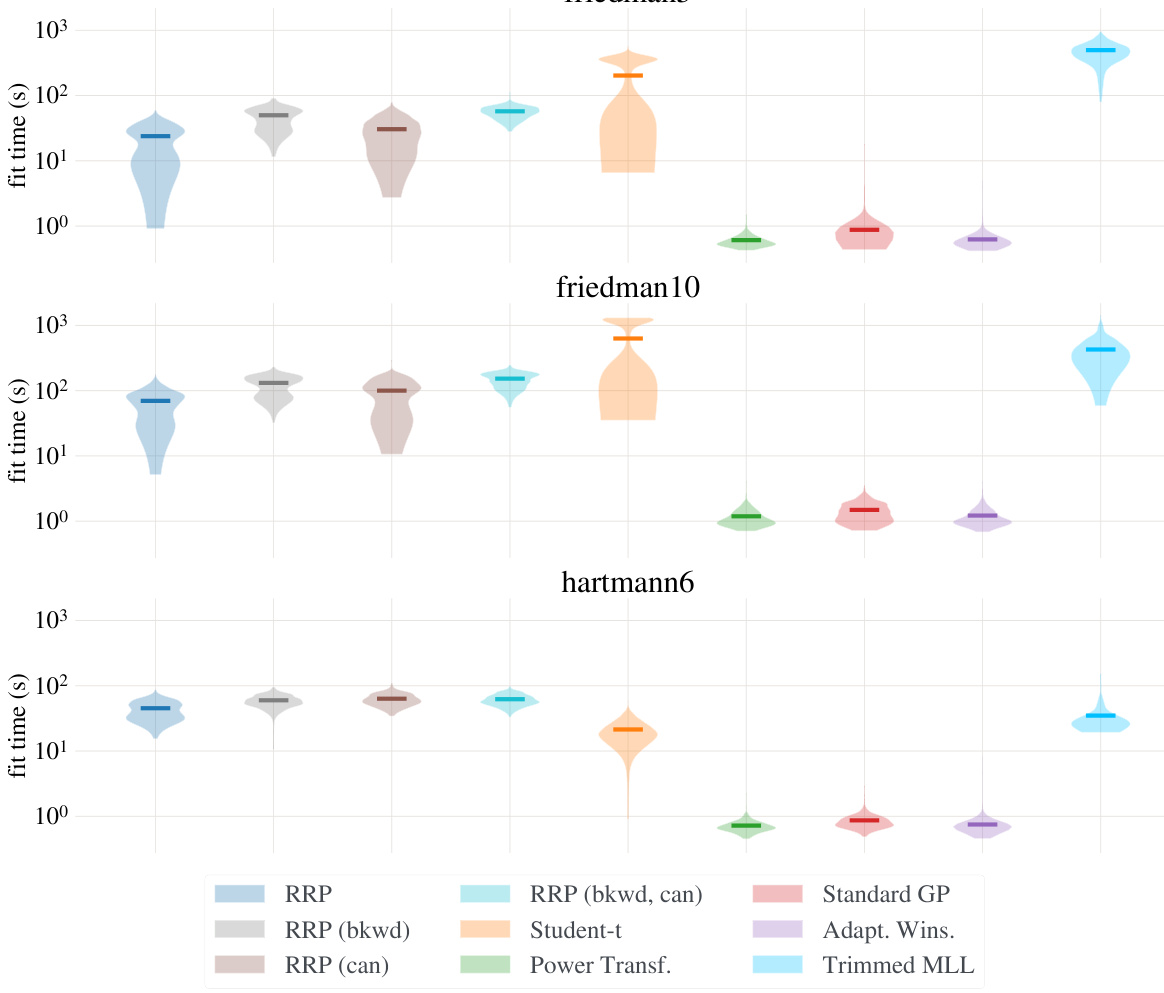
This table compares the negative log marginal likelihood achieved by using two different parameterizations (canonical and convex) of the data-point-specific noise variances ((\rho)) when optimizing with the L-BFGS algorithm. The table shows that the convex parameterization consistently results in a better (lower) negative log marginal likelihood value for various convergence tolerance values ((ftol)). This highlights the benefits of the proposed convex parameterization for improving model optimization.
In-depth insights#
Relevance Pursuit GPs#
Relevance Pursuit Gaussian Processes (GPs) offer a novel approach to robust GP regression by addressing the limitations of standard GPs which assume homoscedastic Gaussian noise. The core idea is to infer data-point specific noise levels, effectively down-weighting outliers without explicit outlier detection. This is achieved via a sequential selection procedure, termed ‘Relevance Pursuit’, that greedily maximizes the marginal log-likelihood. A key theoretical contribution is the proof of strong concavity of the marginal likelihood under a specific parameterization, leading to approximation guarantees for the algorithm. Unlike many robust GP methods, Relevance Pursuit GPs handle sparse outliers effectively and are computationally efficient, showcasing strong empirical performance across various regression and Bayesian optimization tasks, particularly in the challenging setting of sparse corruptions within the function range.
Robustness Guarantees#
The concept of “Robustness Guarantees” in the context of a machine learning model, specifically Gaussian Processes (GPs), is crucial. It speaks to the model’s ability to maintain accuracy and reliability despite noisy or corrupted data. Standard GPs assume homoscedastic Gaussian noise, a limitation in real-world scenarios. The paper likely explores how modifications to standard GP models, such as incorporating data-point-specific noise variances or alternative noise distributions (e.g., Student’s t), improve robustness. Theoretical guarantees are valuable as they move beyond empirical observations, providing mathematical proof of a model’s ability to handle certain types and amounts of data corruption. The authors likely derive these guarantees by leveraging properties like strong concavity of the log marginal likelihood, and linking this to approximation guarantees of algorithms like greedy sequential selection. This is a significant contribution as it provides confidence in the model’s performance under uncertainty, and it addresses a key limitation of traditional GP models.
Concave MLL#
The concept of a concave marginal log-likelihood (MLL) in the context of robust Gaussian processes is counterintuitive. Standard Gaussian process models typically yield a convex MLL, facilitating straightforward optimization. However, the introduction of data-point-specific noise variances, designed to enhance robustness against outliers, can lead to non-convexity in the optimization landscape. The paper’s innovation lies in demonstrating that under a specific parameterization, strong concavity of the MLL can be achieved. This is a crucial result as strong concavity guarantees a unique global optimum, thereby significantly simplifying the optimization problem and providing provable approximation guarantees for the proposed greedy algorithm. The theoretical analysis supporting this concavity is a significant contribution, demonstrating a previously unexplored property within this field and underpinning the algorithm’s reliable performance. This concavity result, therefore, is not merely a mathematical curiosity but a key enabler for the practical effectiveness of the proposed robust Gaussian process model.
BO Applications#
Bayesian Optimization (BO) is a powerful tool for optimizing expensive-to-evaluate black-box functions, and its application to various real-world problems is a significant area of research. A section on ‘BO Applications’ would explore diverse use cases, highlighting the advantages of BO in scenarios with limited data or computational resources. Key applications include hyperparameter tuning in machine learning models, where BO efficiently searches the vast space of hyperparameter combinations to find optimal configurations. Robustness to noise and outliers is crucial in real-world settings, making the integration of robust BO methods, such as those explored in this paper (e.g., using robust Gaussian processes), particularly valuable for real-world applications. Other applications could span robotics, where BO is used for controlling robotic movements and automating tasks, materials science, for discovering novel materials with desired properties, and finance, to optimize investment strategies and risk management. The section would also analyze the performance and limitations of BO across various application domains and discuss challenges associated with scalability and generalization, particularly the inherent difficulties in handling complex, high-dimensional problems. A strong emphasis should be placed on comparing the performance of standard BO approaches with robust BO variants in the presence of real-world noise and outliers, showcasing the practical advantages of robust methods in real-world scenarios. The section’s conclusion would summarize the strengths and potential limitations of BO, highlighting areas for future research and development.
Future Extensions#
The authors propose several promising future research directions. Bayesian model averaging could enhance the robustness of RRP by combining predictions from multiple models, weighting them based on their posterior probabilities. Applying RRP to more complex models, such as scalable learning-curve models for AutoML, would broaden its applicability and impact. The general algorithmic approach of combining greedy optimization with Bayesian model selection, coupled with the convex parameterization technique, could be fruitfully applied to other machine learning models, potentially leading to theoretical guarantees and performance improvements for a wide range of Bayesian methods. The paper mentions investigating forward-backward greedy algorithms for more efficient subset selection. Finally, exploring the relationship between the model’s RIP conditions and its practical performance warrants further investigation.
More visual insights#
More on figures
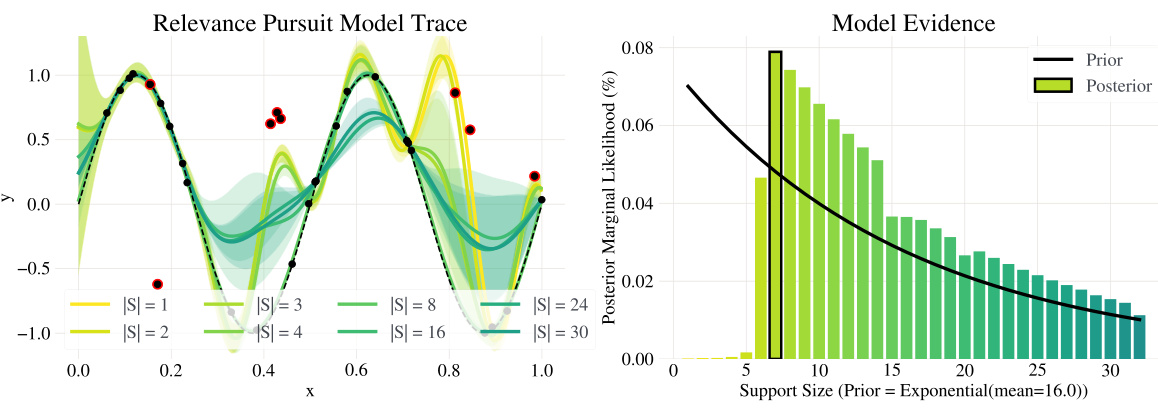
The left panel shows how the model’s posterior distribution evolves as more data points are considered as potential outliers by the Relevance Pursuit algorithm. Each line represents the posterior distribution for different numbers of potential outliers, starting with one and increasing to 30. The red points highlight the locations of artificially introduced corruptions in the data. The right panel displays a bar chart showing the marginal likelihood for models with varying numbers of potential outliers. The model with the highest marginal likelihood, which is the preferred model, is highlighted in black.

The left panel of the figure shows how the model posterior evolves as more data points are included in the model. The right panel shows the posterior marginal likelihood as a function of the number of data points included in the model.
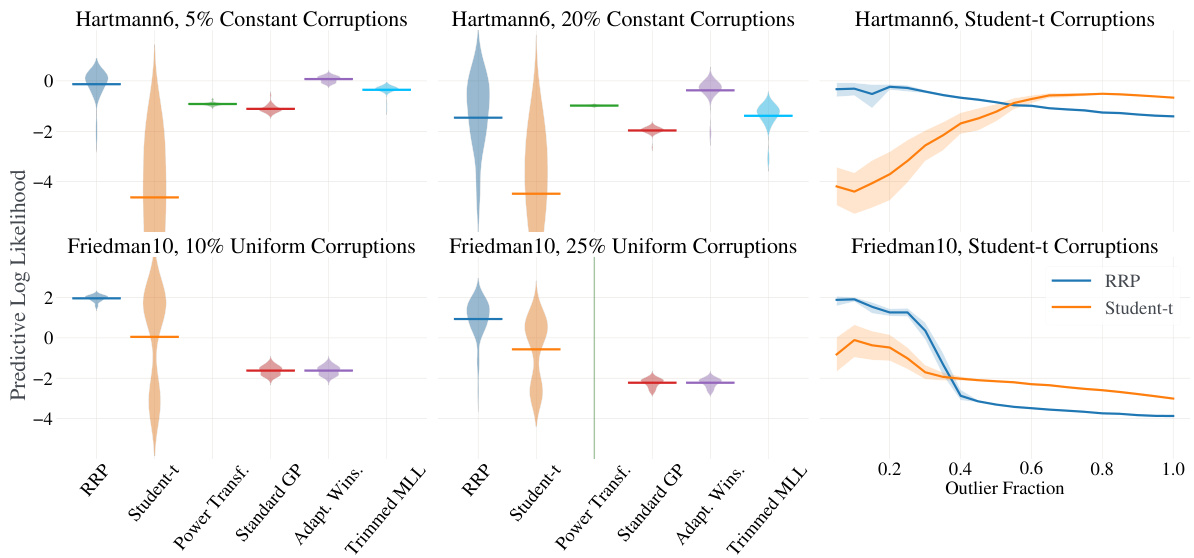
The figure compares the performance of different robust Gaussian process regression methods on synthetic datasets. The left panel shows the distribution of predictive log-likelihood for each method, highlighting RRP’s superior performance, especially with high corruption levels. The right panel shows how predictive log-likelihood changes with increasing corruption probability, emphasizing RRP’s robustness to label corruptions.

This figure shows two plots. The left plot visualizes the evolution of the model posterior during the Relevance Pursuit algorithm. The algorithm iteratively adds data points as potential outliers, indicated by increasing data-point-specific noise variance. The lines represent different stages of the algorithm. Red points show corrupted data points that were generated randomly within the range of the function. The right plot illustrates the marginal likelihood as a function of the number of outliers (S). The model with the highest marginal likelihood is the preferred model, as indicated by the black box.
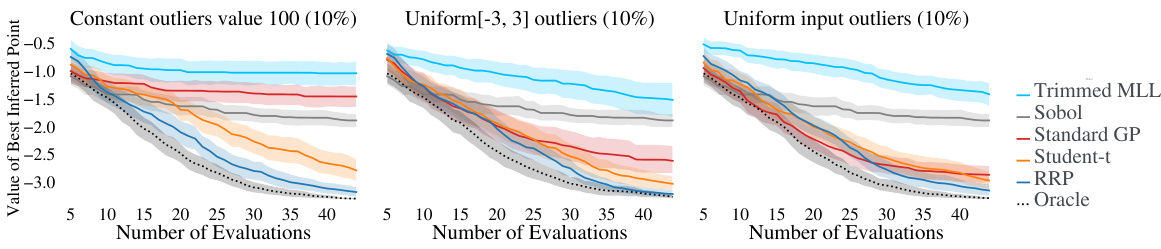
This figure shows the results of Bayesian Optimization (BO) experiments on the Hartmann6 test function with three different types of label corruptions: constant outliers, uniform outliers, and uniform input outliers. The x-axis represents the number of evaluations and the y-axis is the value of the best inferred point found so far. The results for various BO algorithms are plotted, including Relevance Pursuit (RRP), an oracle that always knows the true uncorrupted value, as well as standard baselines like a standard GP, and a Student-t likelihood model. The results show that Relevance Pursuit performs competitively in most cases, even when the corruptions are harder to detect (like uniform input outliers).

The left panel shows how the model posterior evolves during the Relevance Pursuit algorithm. As the number of data points with adjusted noise variances increases, the model’s fit improves, adapting to the corrupted data points (shown in red). The right panel shows how the posterior marginal likelihood varies with the number of data points with adjusted noise variances. The algorithm selects the model with the highest marginal likelihood (boxed in black).
The figure shows two plots. The left plot displays the evolution of the model posterior during the Relevance Pursuit algorithm. As the number of data-point-specific noise variances increases, the model’s fit improves. Red points in the plot highlight corruptions that were randomly generated within the function’s range. The right plot compares the posterior marginal likelihoods for different model sizes. The model with the highest marginal likelihood is chosen as the preferred model.
The left panel of the figure shows how the model’s posterior changes as more data-point-specific noise variances are added using the Relevance Pursuit algorithm. The algorithm iteratively adds data points whose individual noise variance maximizes the marginal likelihood. The red points are corrupted data points. The right panel shows how the posterior marginal likelihood changes as a function of the model’s support size (the number of data points with non-zero noise variances). The algorithm selects the model with the maximum marginal likelihood, indicated by the black box.
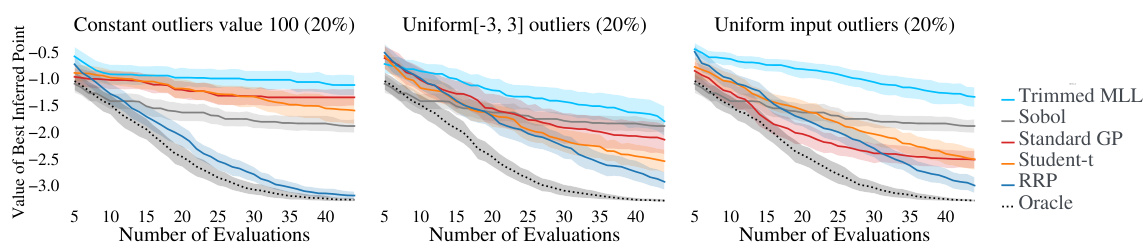
This figure shows the results of Bayesian optimization (BO) experiments on the Hartmann6 test function with three different types of label corruption: constant outliers, outliers uniformly sampled from [-3, 3], and outliers uniformly sampled from the function’s input domain. The results compare the performance of several BO methods, including Relevance Pursuit (RRP), showing that RRP performs favorably across various corruption settings, often approaching or matching the performance of an ‘oracle’ that has access to uncorrupted labels.
More on tables

This table compares the mean absolute error (MAE) of different Gaussian Process regression models, including the proposed Robust Gaussian Processes via Relevance Pursuit (RRP) method and existing methods such as standard GP, Student-t GP, and RCGP on several datasets with various types of label corruptions (no outliers, uniform outliers, asymmetric outliers, and focused outliers). The results demonstrate that RRP is competitive with other methods and significantly outperforms them in the presence of uniform and asymmetric outliers.
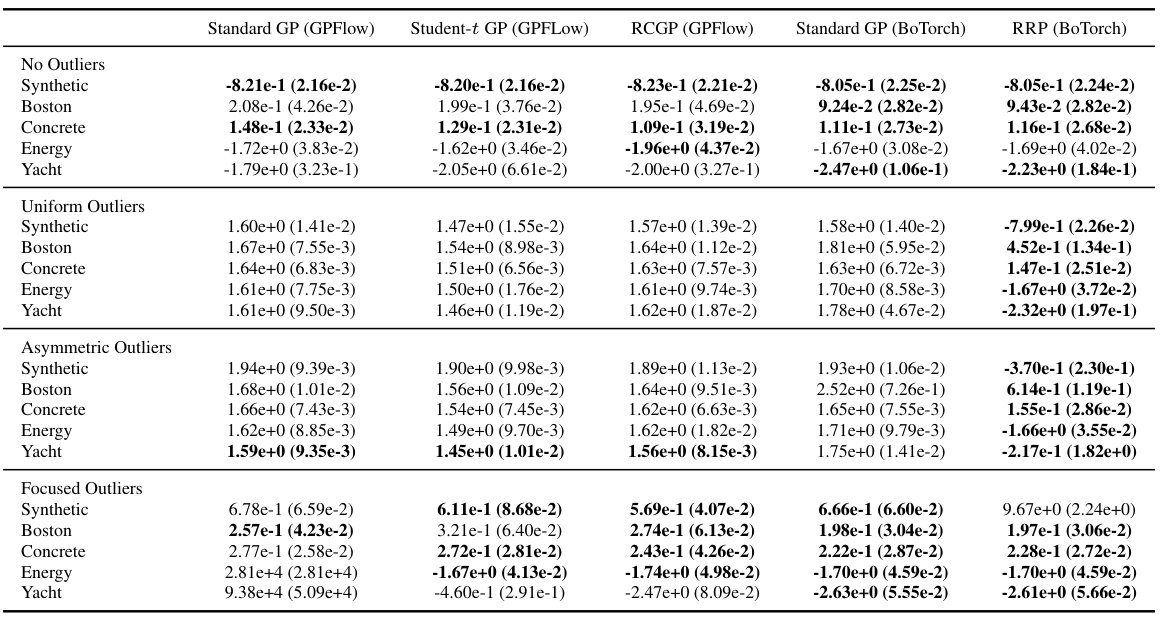
This table compares the mean absolute error (MAE) of different Gaussian process regression models on various datasets with different types of outliers (no outliers, uniform outliers, asymmetric outliers, and focused outliers). The models compared include a standard Gaussian process, a Student-t Gaussian process, a robust conjugate Gaussian process (RCGP), and the proposed Robust Gaussian Processes via Relevance Pursuit (RRP) method. The results show that RRP is competitive with other methods and significantly outperforms them when outliers are uniformly or asymmetrically distributed.
This table presents the Mean Absolute Error (MAE) results for several robust Gaussian process regression methods, including the proposed Relevance Pursuit (RRP) method, on various datasets with different types of label corruptions (no outliers, uniform outliers, asymmetric outliers, and focused outliers). The results show how the methods perform under various noise conditions and compares RRP to state-of-the-art methods.
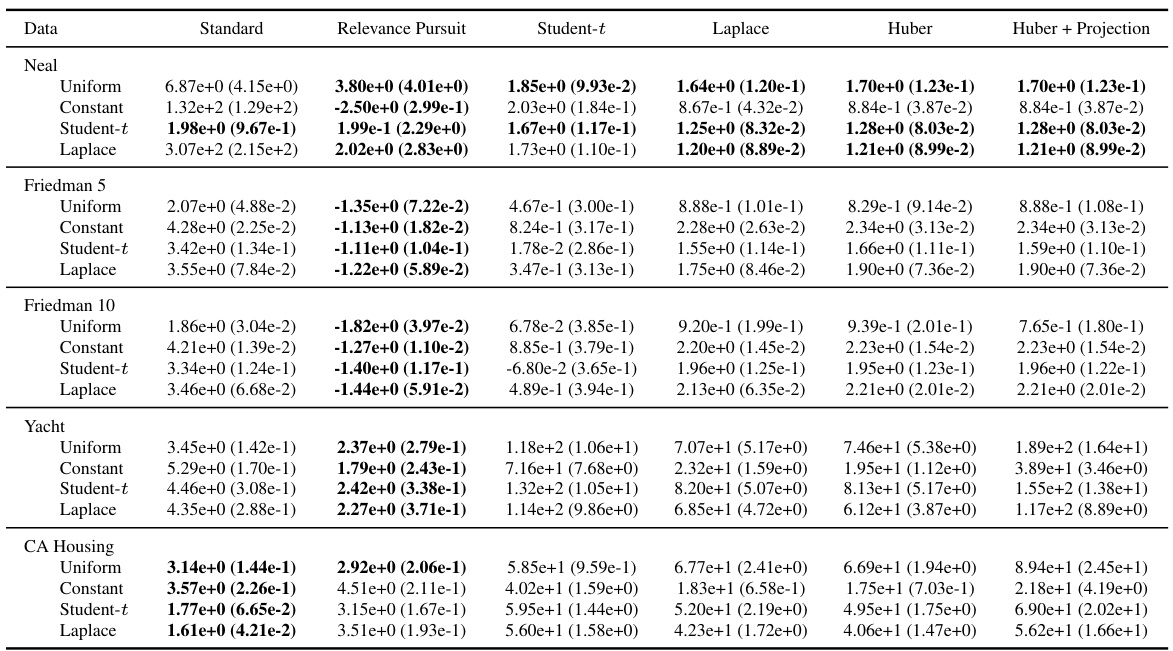
This table presents the Mean Absolute Error (MAE) for various regression models on several datasets. The models are compared under different noise conditions: no outliers, uniform outliers, asymmetric outliers, and focused outliers. The table shows that the proposed Relevance Pursuit (RRP) method is competitive with other methods and significantly outperforms them in the presence of uniform and asymmetric outliers.
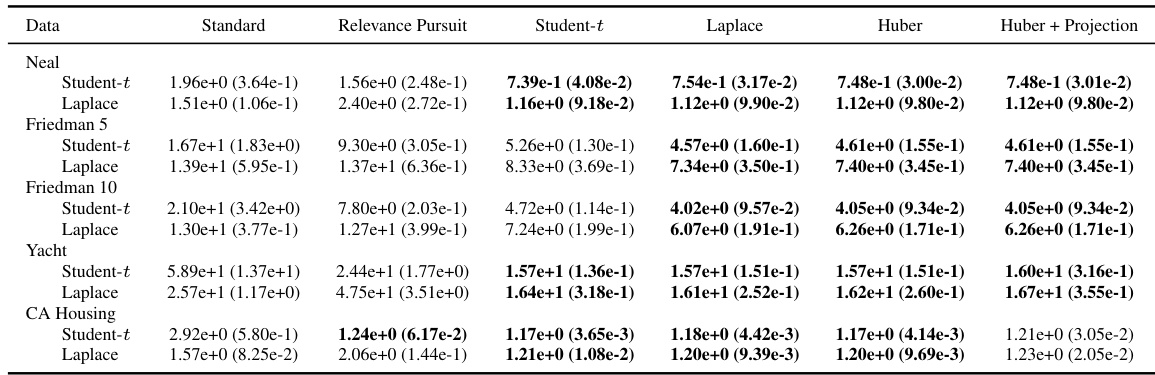
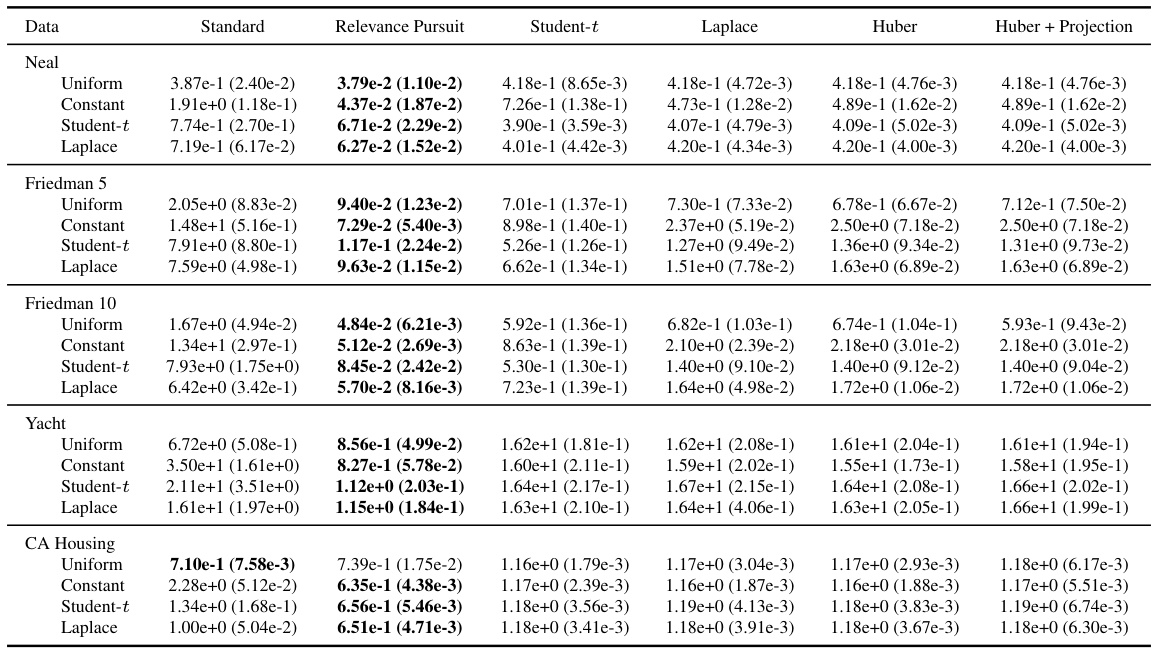
This table compares the root mean square error (RMSE) of different robust Gaussian process regression models on several datasets with 15% label corruption. The models compared are a standard Gaussian process, Relevance Pursuit, a Student-t likelihood GP, a Laplace likelihood GP, a Huber likelihood GP, and a Huber likelihood GP with projection statistics. Results are shown for various types of outliers (uniform, constant, Student-t) across multiple datasets (Neal, Friedman 5, Friedman 10, Yacht, CA Housing).

This table compares the mean absolute error (MAE) of several robust Gaussian process regression models, including the proposed Relevance Pursuit (RRP) method, on various datasets with different types of label corruptions (no outliers, uniform outliers, asymmetric outliers, and focused outliers). The results show that RRP is competitive with other methods and significantly outperforms them in cases with uniform and asymmetric outliers.
Full paper#