↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional Computerized Adaptive Testing (CAT) focuses primarily on accurate individual ability estimation. However, this paper highlights a critical issue: inconsistent student rankings even when individual ability estimates are accurate. This is because CAT typically tests students independently. The lack of consistent ranking undermines fairness and utility in high-stakes exams.
This paper introduces Collaborative Computerized Adaptive Testing (CCAT), a novel framework that leverages inter-student information to improve ranking consistency. By incorporating collaborative student data as anchors, CCAT enhances both question selection and ability estimation. The authors provide theoretical guarantees and empirical evidence supporting CCAT’s ability to significantly improve ranking accuracy, particularly in short tests.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in Computerized Adaptive Testing (CAT) and educational assessment. It addresses the critical issue of ranking consistency in CAT, which is often overlooked despite its importance in high-stakes exams. The proposed CCAT framework offers a novel solution and opens avenues for future research focusing on collaborative learning and improved ranking accuracy. The theoretical guarantees and experimental validation provide strong evidence of its efficacy. This work is relevant to current trends in AI-driven education and personalized assessment.
Visual Insights#

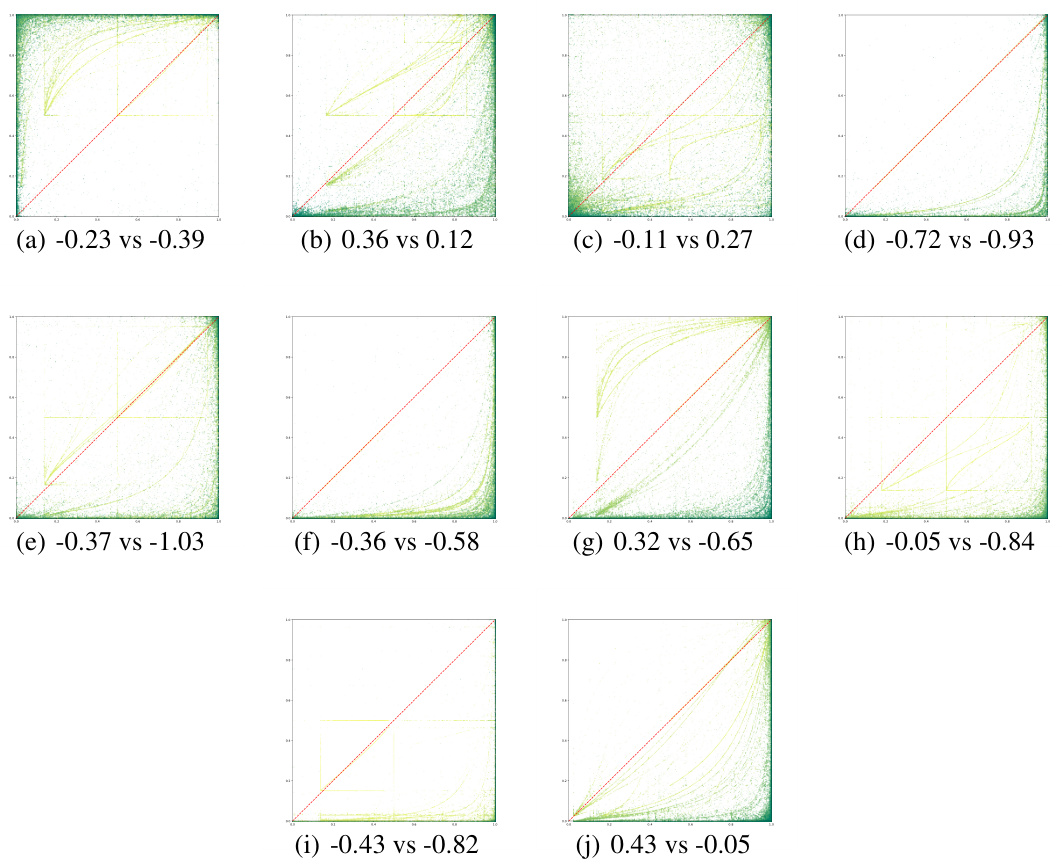
The figure demonstrates that minimizing the mean squared error (MSE) in ability scores does not guarantee accurate student ranking. Subfigure (a) shows a GRE score report and an example illustrating this point. Subfigure (b) compares several state-of-the-art Computerized Adaptive Testing (CAT) methods and shows that even the best-performing methods in terms of MSE may perform no better than random guessing when it comes to student ranking.
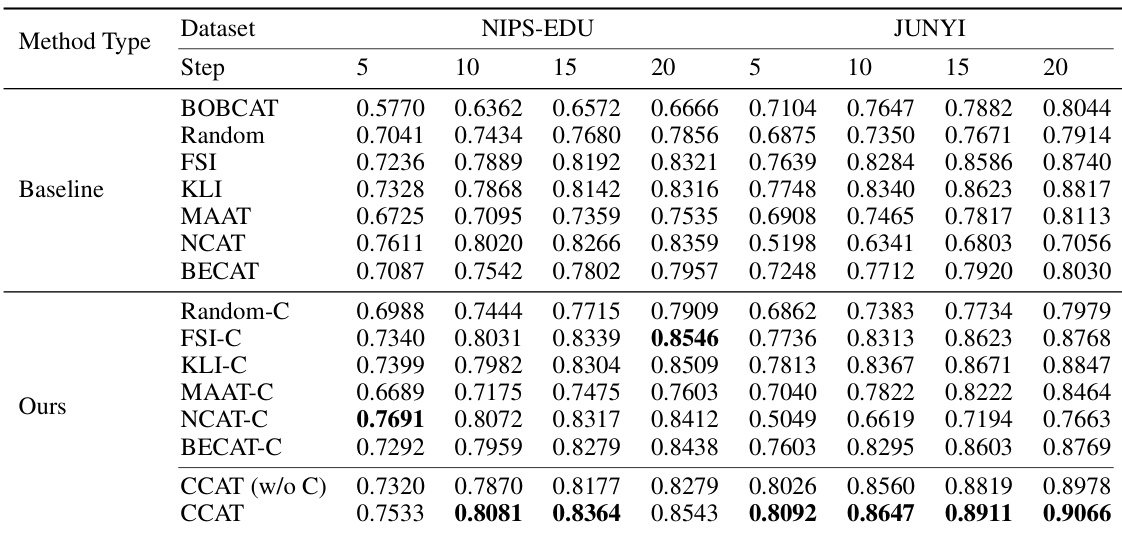
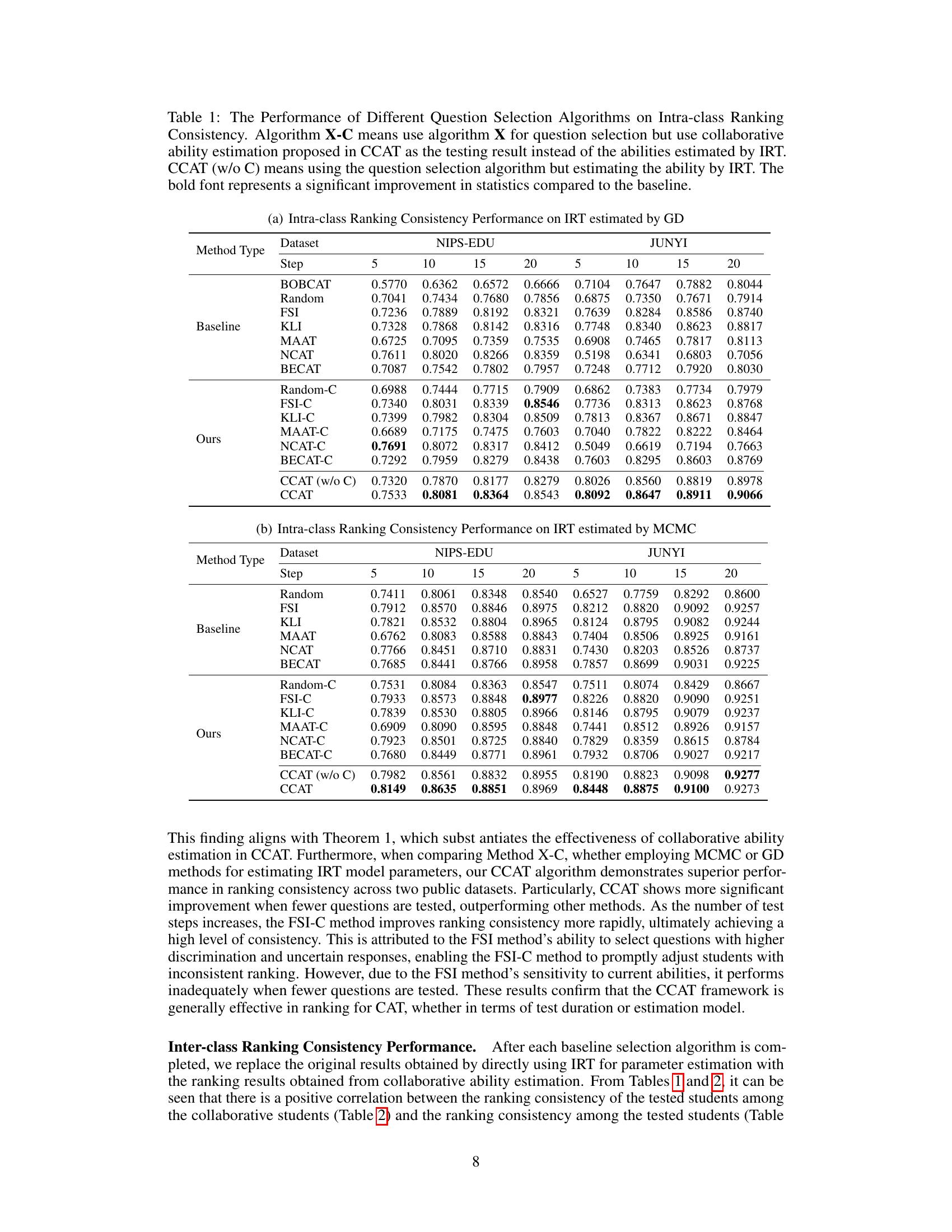
This table presents the performance comparison of various question selection algorithms on intra-class ranking consistency. It shows the results for different algorithms (including those using collaborative ability estimation) across two datasets (NIPS-EDU and JUNYI) and varying numbers of test steps. The bold values indicate statistically significant improvements over the baseline.
In-depth insights#
CAT Ranking Issue#
The core issue in Computerized Adaptive Testing (CAT) lies not solely in precise ability estimation, but also in reliable student ranking. While minimizing mean squared error (MSE) in ability scores is a common goal, it doesn’t guarantee accurate rank ordering. High accuracy doesn’t translate to consistent ranking, as even state-of-the-art CAT methods can produce rankings similar to random chance. This inconsistency stems from the independent testing paradigm of traditional CAT, where student responses are analyzed in isolation. The inherent asynchronicity and lack of information sharing between tests exacerbate this problem, preventing the use of holistic data to improve ranking accuracy. This highlights a need for innovative CAT frameworks that address ranking directly, rather than relying on ability estimation as a proxy. The challenge lies in developing methods that can guarantee ranking consistency while efficiently estimating student abilities, particularly in high-stakes scenarios where accurate ranking is paramount.
CCAT Framework#
The Collaborative Computerized Adaptive Testing (CCAT) framework offers a novel approach to address limitations in traditional CAT by incorporating inter-student information to enhance student ranking. Unlike conventional independent testing, CCAT leverages collaborative students as anchors, utilizing their performance data to inform question selection and ability estimation for the tested student. This collaborative learning paradigm directly tackles the challenge of ranking consistency in CAT, providing theoretical guarantees and experimental validation to support its effectiveness. The framework’s core innovation lies in its ability to integrate inter-student information, thereby generating more consistent and reliable student rankings, especially valuable in high-stakes examination settings. The theoretical analysis substantiates its effectiveness, demonstrating improved ranking consistency compared to existing methods. A key strength of CCAT is its adaptability, as it can integrate with diverse existing question selection algorithms, making it a flexible and versatile tool for improving the accuracy and fairness of computerized adaptive assessments.
Theoretical Analysis#
A theoretical analysis section in a research paper would typically delve into a formal mathematical or logical examination of the proposed method or model. It aims to provide a rigorous justification for the claims made, going beyond empirical observations. This might involve deriving key properties, proving theorems, or establishing bounds on performance. A strong theoretical analysis would ideally provide guarantees on the model’s behavior, explain its strengths and weaknesses, and compare it to existing approaches in a formal way. Assumptions made in the analysis should be clearly stated and their implications discussed. The analysis may include approximations or simplifications to make the problem tractable, which should be justified and the potential impact on the results assessed. Ultimately, a robust theoretical analysis enhances the credibility and understanding of the research, providing deeper insights beyond simple experimental results.
Empirical Results#
An Empirical Results section in a research paper should present a thorough evaluation of the proposed method. It should compare the results against existing state-of-the-art techniques using appropriate metrics and statistical tests, clearly demonstrating superior performance or significant improvements. Furthermore, the section needs to include a discussion of the results’ implications, addressing the research questions posed in the introduction. Robustness analyses, exploring the impact of variations in experimental settings, are crucial. The discussion should acknowledge any limitations of the study and suggest future research directions, ensuring a balanced presentation. High-quality visualizations such as graphs and tables are essential to present complex results clearly and efficiently, supporting the claims made and enabling easy comprehension by the reader. Ideally, the results should not only confirm the hypotheses but also offer novel insights into the problem being investigated, potentially leading to a broader understanding.
Future Works#
Future work in computerized adaptive testing (CAT) should prioritize enhancing ranking consistency, especially in short tests where current methods struggle. Addressing the inherent dilemma of aligning test outcomes with true abilities is crucial. Improving the accuracy of ability estimation while maintaining fair ranking is a key challenge. Further research could explore more sophisticated question selection algorithms that leverage inter-student information more effectively within the collaborative framework. Theoretical guarantees for ranking consistency across different student populations and question sets need to be strengthened. Finally, extensive real-world validation and a deeper analysis of the impact on various high-stakes testing scenarios are essential for broad acceptance and implementation of these improvements.
More visual insights#
More on figures
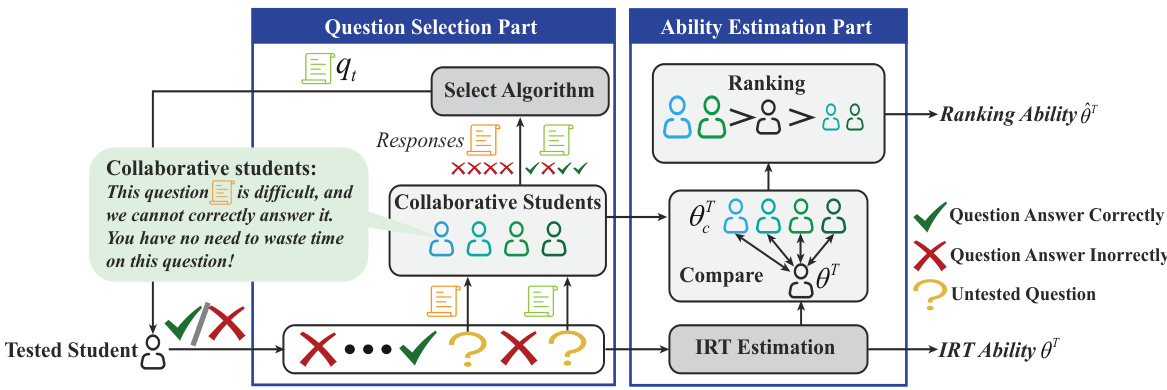
The figure illustrates the CCAT framework, which has two main parts: question selection and ability estimation. In the question selection part, the performance of collaborative students on various questions is used to select suitable questions for the tested student. The ability estimation part then ranks the tested student against the collaborative students, using this ranking as the final test score. This collaborative approach aims to improve the accuracy and consistency of student ranking in computerized adaptive testing.
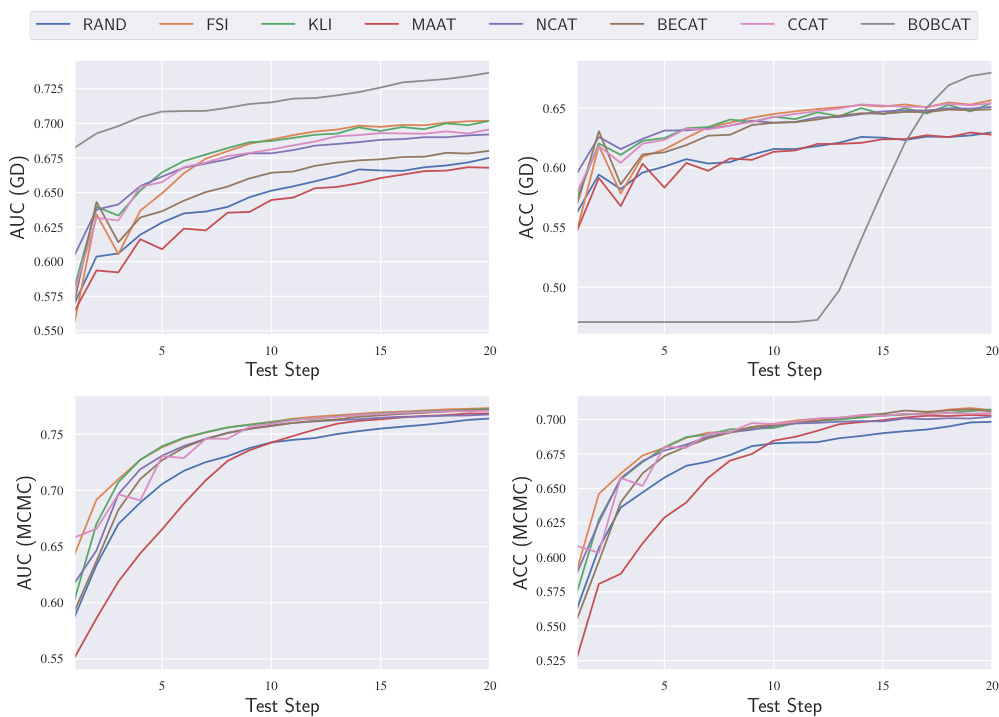
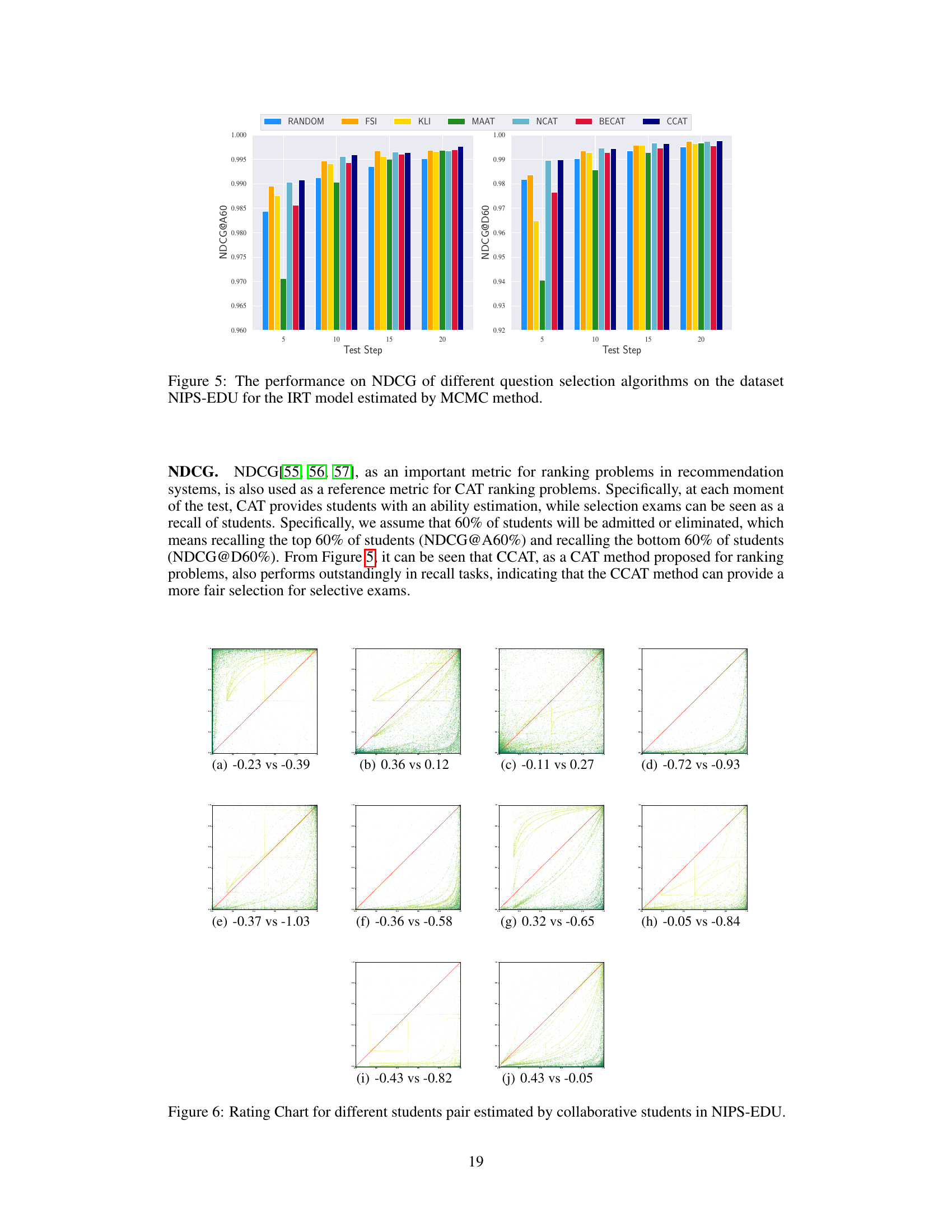
This figure shows the accuracy (ACC) and area under the ROC curve (AUC) of different question selection algorithms (Random, FSI, KLI, MAAT, NCAT, BECAT, CCAT, BOBCAT) on the NIPS-EDU dataset. The performance is evaluated using the Item Response Theory (IRT) model, with parameters estimated by both Markov Chain Monte Carlo (MCMC) and Gradient Descent (GD) methods. The x-axis represents the test step, and the y-axis represents the ACC and AUC values. This visualization helps to compare the effectiveness of various question selection algorithms in terms of both accuracy and ranking performance of students.
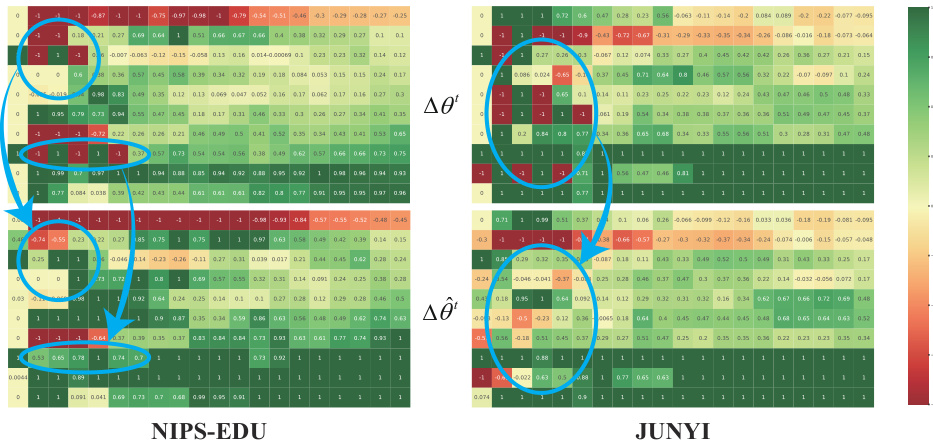
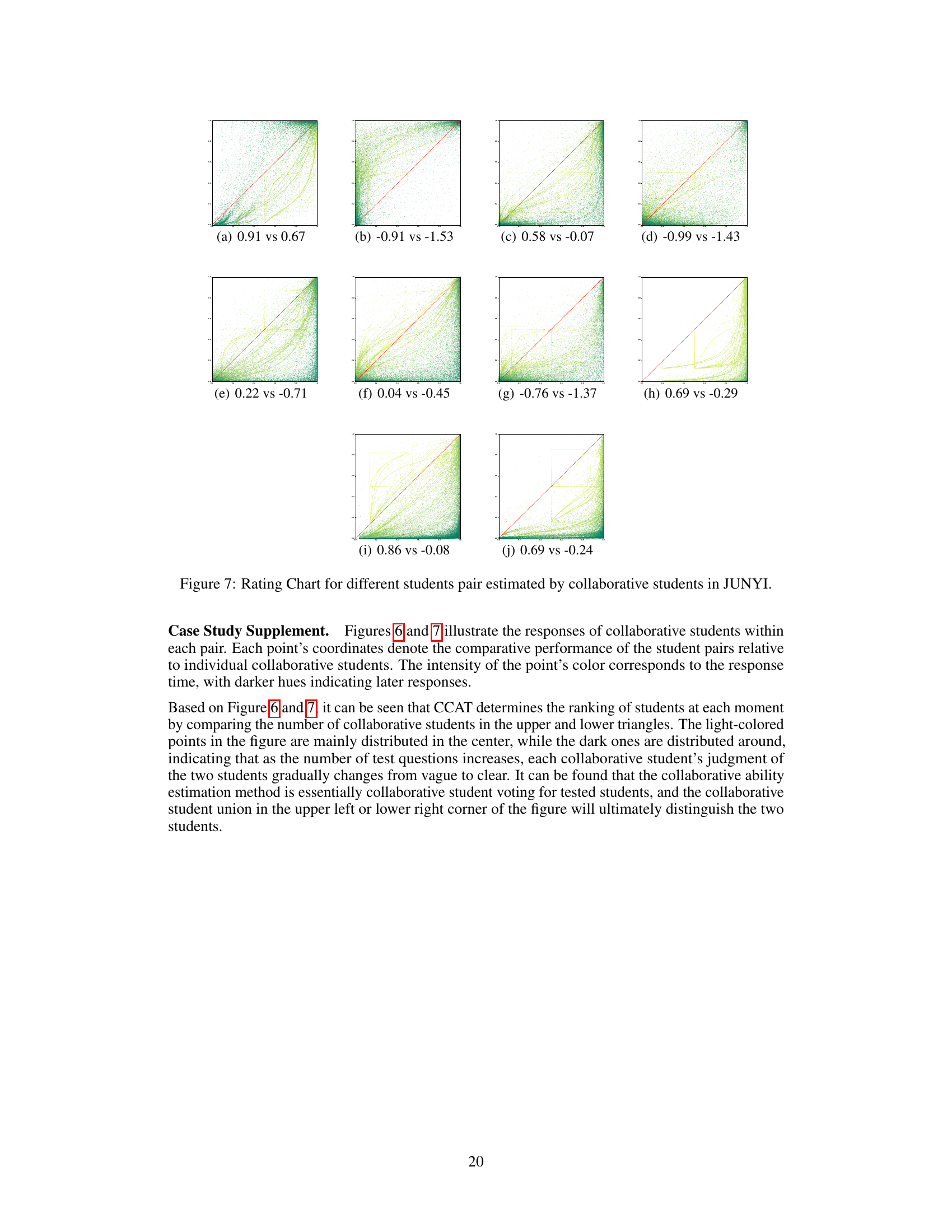
This figure visualizes the differences in ability estimation between the IRT method and the CCAT method for student pairs from the NIPS-EDU and JUNYI datasets. Each cell represents the difference in estimated ability between two students in a pair. Redder colors indicate larger differences, and the visualization helps demonstrate the improved ranking consistency achieved with CCAT, especially when comparing the results of IRT estimation done with GD and MCMC methods. The results suggest that CCAT is superior to IRT with GD when considering ranking consistency.
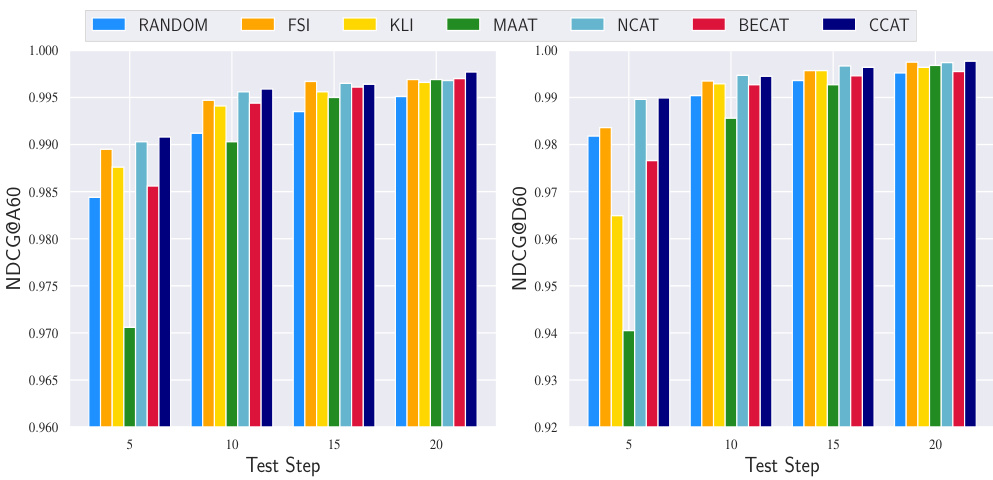
This figure shows the performance of different question selection algorithms (Random, FSI, KLI, MAAT, NCAT, BECAT, and CCAT) on the NIPS-EDU dataset. The performance is measured using two metrics: Accuracy (ACC) and Area Under the Curve (AUC). The results are shown separately for two methods of estimating Item Response Theory (IRT) parameters: Markov Chain Monte Carlo (MCMC) and Gradient Descent (GD). This allows for a comparison of the algorithms’ performance under different IRT estimation methods. The x-axis shows the test step (number of questions asked) and the y-axis represents the ACC or AUC values. The figure helps demonstrate the effectiveness of different question selection techniques and how their performance is affected by the method used for IRT parameter estimation.
This figure visualizes the differences in ability estimation between the IRT method and the CCAT method for pairs of students. It demonstrates that CCAT offers superior discrimination, especially when the goal is ranking consistency in CAT. The visualization uses a heatmap to show the difference in estimated ability between pairs of students, highlighting instances where the ranking is inconsistent (indicated by red).

This figure visualizes the differences in ability estimation between the IRT method and the CCAT method for student pairs. It shows that the CCAT method provides better discrimination in ability estimation, particularly when the ranking consistency of CAT is taken into account. This improvement is achieved by using collaborative students to assist in ranking test-takers.
More on tables
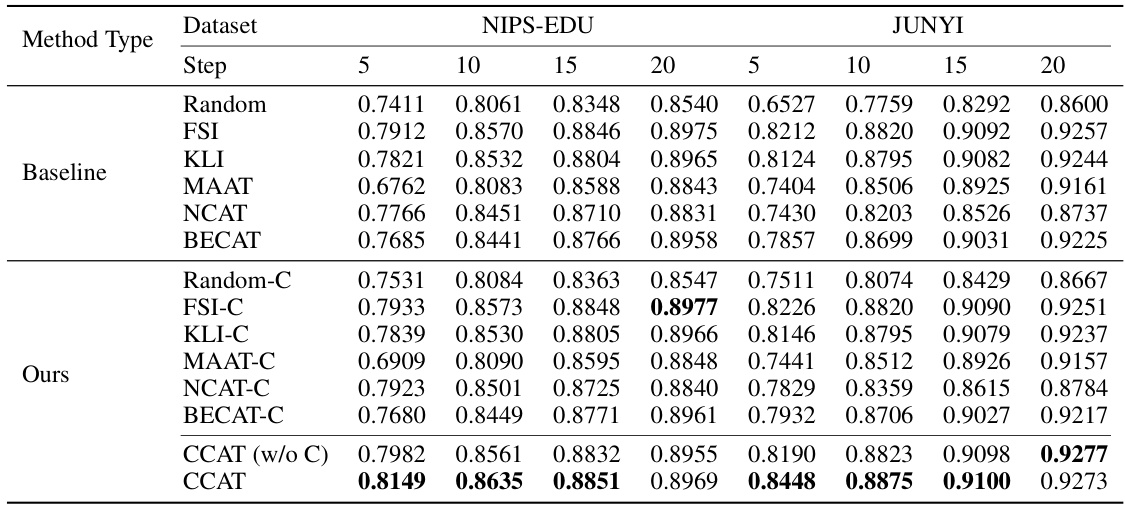
This table presents the performance comparison of different question selection algorithms on intra-class ranking consistency. It shows the results for both the original IRT-based ability estimation and the proposed CCAT’s collaborative ability estimation method. The table is split into subsections for different IRT estimation methods (GD and MCMC) and shows results across various testing steps (5, 10, 15, 20). The bold numbers highlight statistically significant improvements over baseline performance.
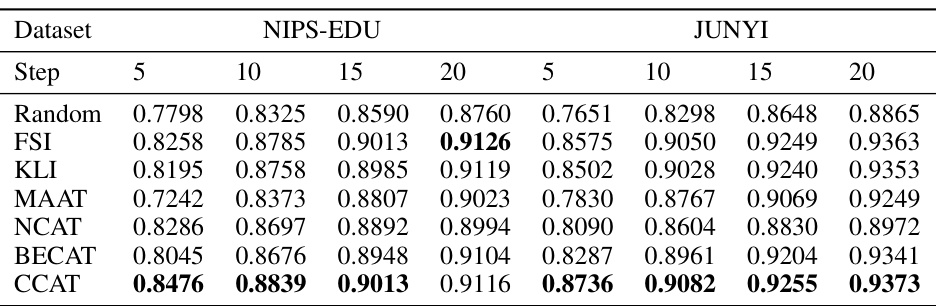
This table presents the results of an experiment comparing different question selection algorithms on their ability to produce consistent intra-class rankings. The algorithms are tested with and without using collaborative ability estimation (CCAT). The results show the ranking consistency performance for various algorithms across two datasets (NIPS-EDU and JUNYI) for different numbers of test steps (5, 10, 15, and 20). The bold values indicate a statistically significant improvement over the baseline.

This table presents the performance comparison of different question selection algorithms on intra-class ranking consistency. It shows the results for two datasets (NIPS-EDU and JUNYI) across various test steps (5, 10, 15, and 20). The comparison includes both traditional methods and those incorporating collaborative ability estimation (indicated by ‘-C’). The table highlights the improvement in consistency offered by the CCAT framework, particularly when using collaborative ability estimation.
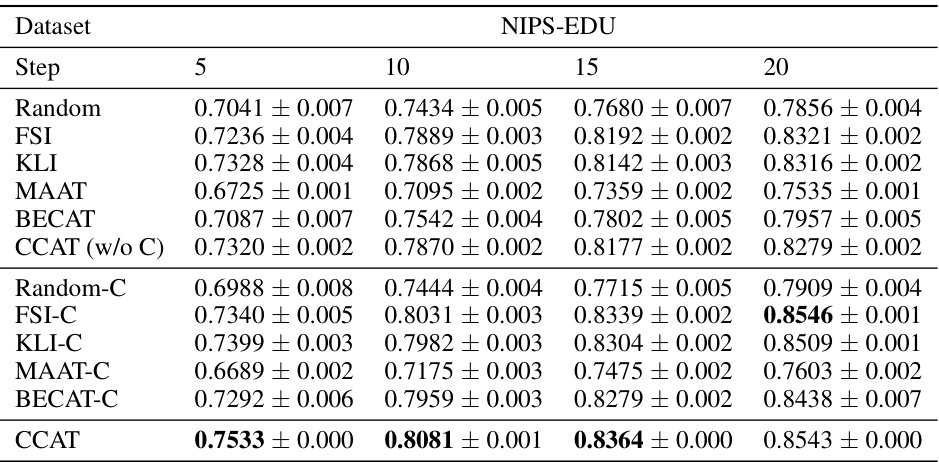
This table presents the performance comparison of different question selection algorithms on intra-class ranking consistency. It shows the results for various algorithms (including those using collaborative ability estimation) across different numbers of test steps (5, 10, 15, 20). The metrics are reported for two datasets, NIPS-EDU and JUNYI, with and without employing collaborative ability estimation. The bold font highlights statistically significant improvements compared to the baseline (Random).

This table presents the performance comparison of various question selection algorithms on intra-class ranking consistency. It shows results for different algorithms (including those using collaborative ability estimation) across two datasets (NIPS-EDU and JUNYI) and varying numbers of test steps (5, 10, 15, 20). The bold numbers highlight statistically significant improvements over the baseline.
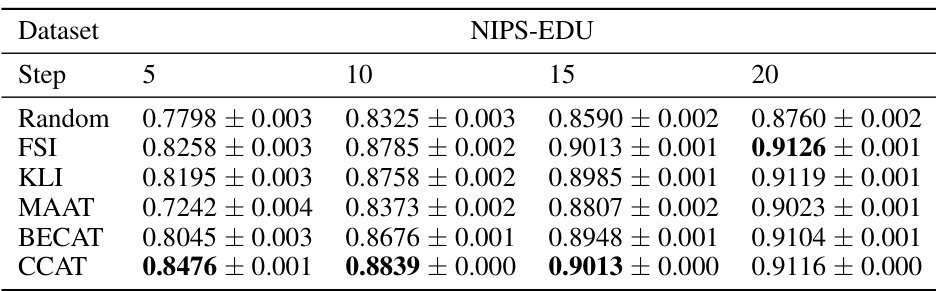
This table presents the performance comparison of various question selection algorithms on the intra-class ranking consistency metric. It compares the performance of algorithms using traditional IRT ability estimation with those using the collaborative ability estimation method introduced in the CCAT framework. The results are shown for different numbers of testing steps (5, 10, 15, and 20) and on two datasets (NIPS-EDU and JUNYI). The boldfaced numbers indicate statistically significant improvements over baseline methods.

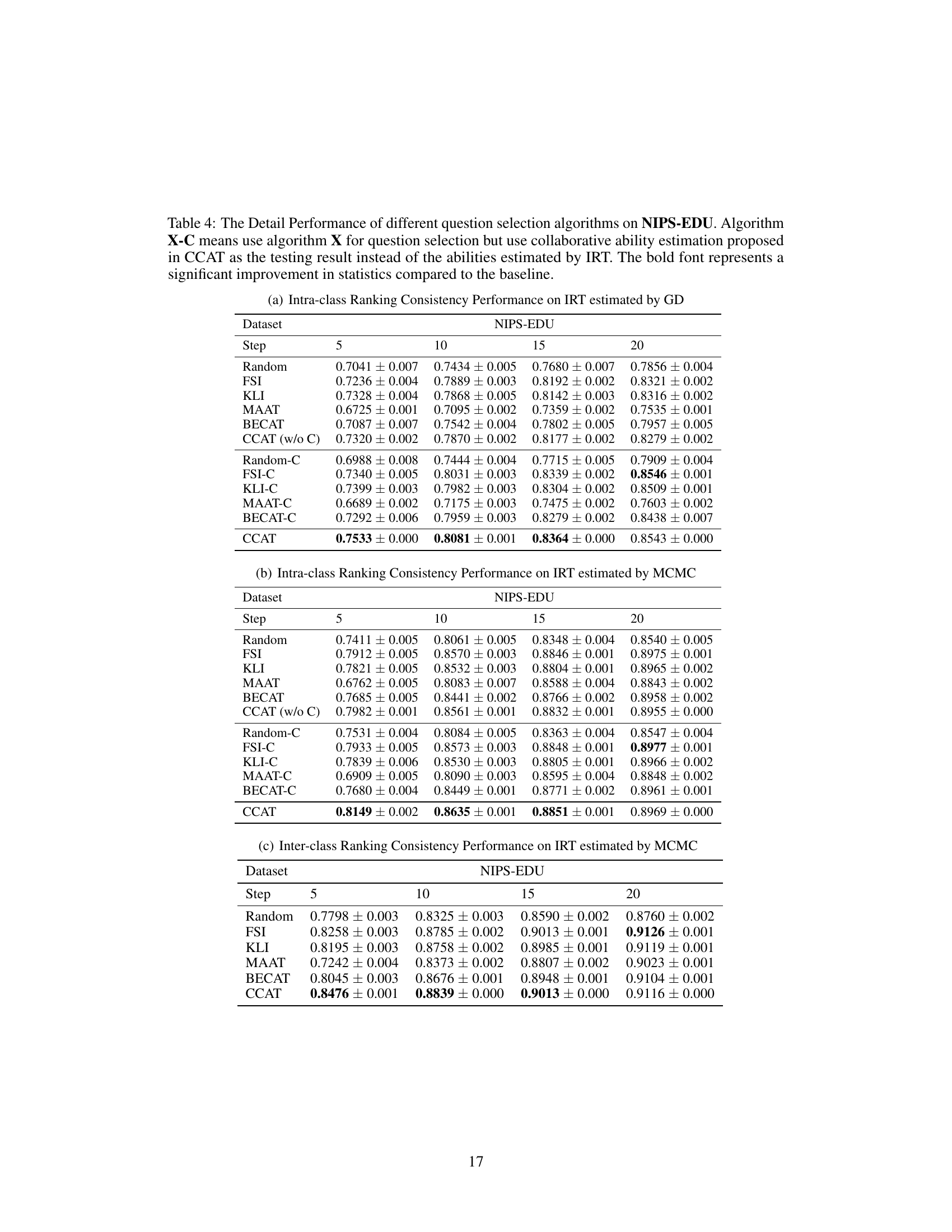
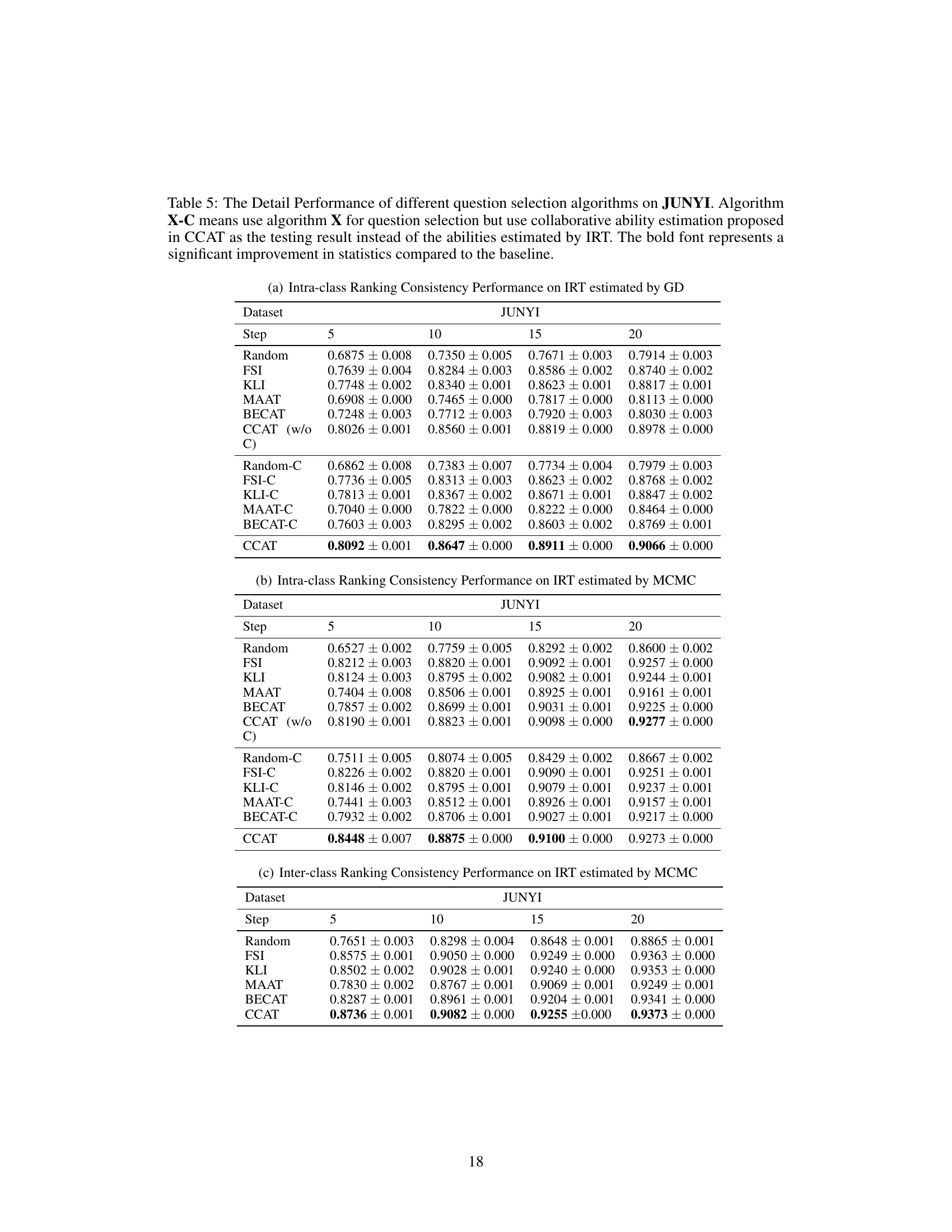
This table presents the detailed performance of different question selection algorithms on the JUNYI dataset. It shows the intra-class and inter-class ranking consistency performance with and without collaborative ability estimation for various test steps (5, 10, 15, 20). The results are broken down by different question selection algorithms (Random, FSI, KLI, MAAT, BECAT, CCAT (without collaborative estimation), Random-C, FSI-C, KLI-C, MAAT-C, BECAT-C, and CCAT) and whether collaborative ability estimation was used. Statistical significance is indicated by bold font, highlighting improvements over the baseline.
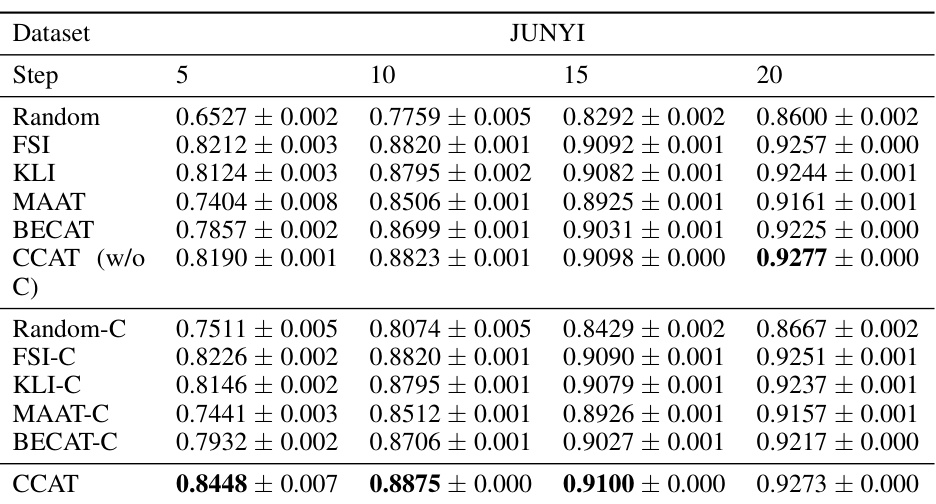
This table presents the performance comparison of various question selection algorithms on intra-class ranking consistency. It shows results for two datasets (NIPS-EDU and JUNYI) and different numbers of test steps (5, 10, 15, and 20). The algorithms are compared both with and without using the collaborative ability estimation method introduced in the CCAT framework. The bold values indicate statistically significant improvements over the baseline.
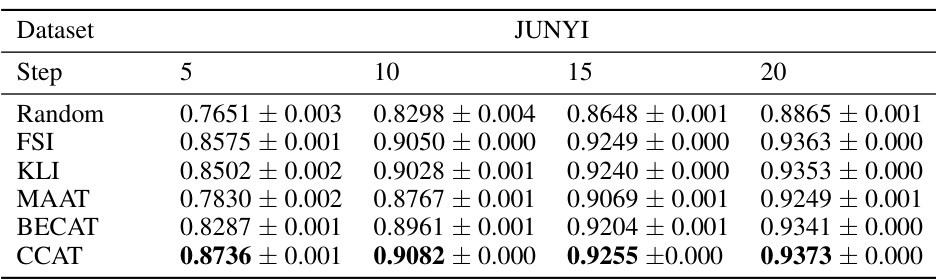
This table presents the detailed performance of different question selection algorithms on the JUNYI dataset. It shows the intra-class and inter-class ranking consistency performance for various algorithms, with and without collaborative ability estimation. The results are broken down by the IRT estimation method used (GD and MCMC) and the number of test steps (5, 10, 15, and 20). Bold values indicate statistically significant improvements compared to a baseline.
Full paper#