↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Exemplar-Free Class Incremental Learning (EFCIL) faces challenges in adapting to new tasks without retaining past data. Existing methods often represent classes as Gaussian distributions but struggle with two key problems. First, they fail to adapt the covariance matrices of classes as the model learns new tasks. Second, they are susceptible to task-recency bias, where the model favors recently seen tasks, often due to a dimensionality collapse of feature representations.
This paper introduces AdaGauss, a novel method that directly addresses these issues. AdaGauss dynamically adapts covariance matrices for each task, ensuring accurate classification. Furthermore, it incorporates a novel anti-collapse loss function to combat dimensionality collapse and reduce task-recency bias. Through extensive experiments, AdaGauss demonstrates state-of-the-art performance on various EFCIL benchmarks. This improvement highlights the importance of adapting covariances and the effectiveness of the anti-collapse loss in achieving robust continual learning.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the critical issues of adapting covariances and mitigating task-recency bias in exemplar-free class incremental learning (EFCIL). These are major hurdles in developing robust and efficient lifelong learning systems. The proposed AdaGauss method offers significant advancements and provides a strong foundation for future research in continual learning.
Visual Insights#
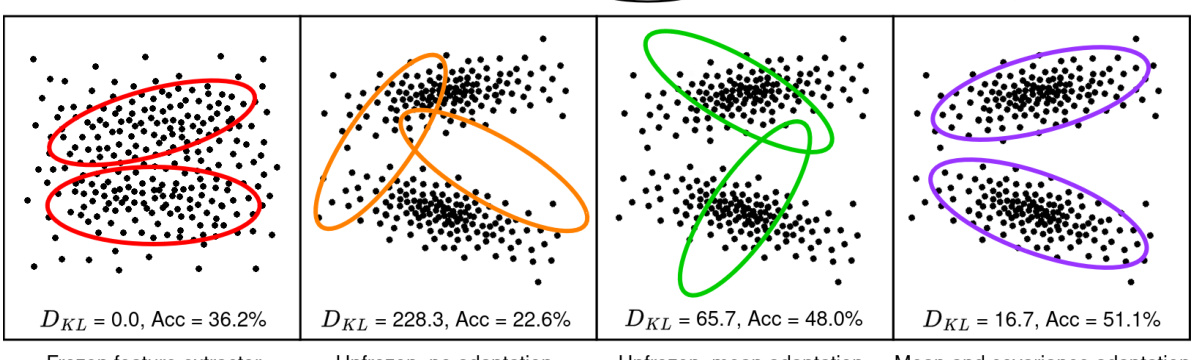
This figure visualizes the latent space representation of classes in a class incremental learning setting using ResNet18 on the ImagenetSubset dataset. It compares four scenarios: a frozen feature extractor (no adaptation), an unfrozen feature extractor with only mean adaptation, an unfrozen feature extractor with mean and covariance adaptation, and the ground truth distributions. It highlights the impact of adapting covariances on class separability and overall accuracy. The frozen model demonstrates significant class overlap. The unfrozen models show a drift in distributions between the ground truth and the model’s learned distributions, underscoring the need for methods which adapt both mean and covariance.
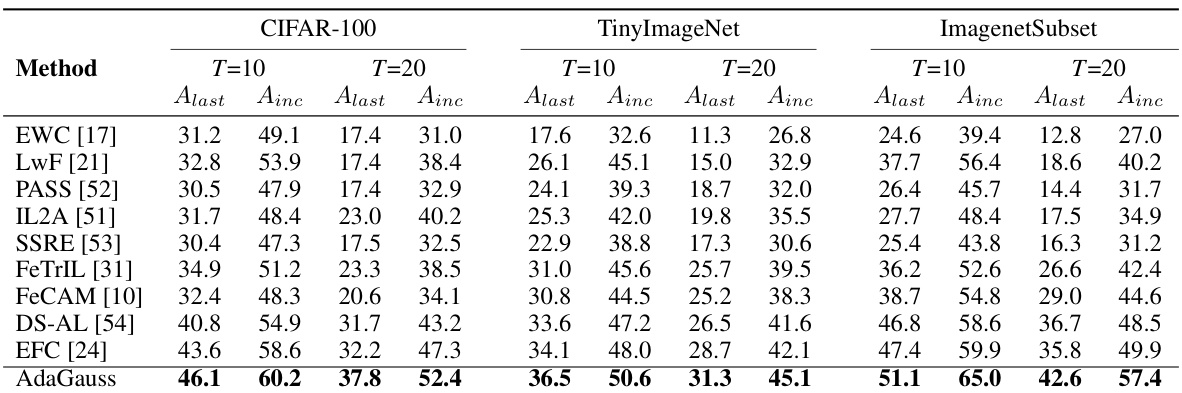
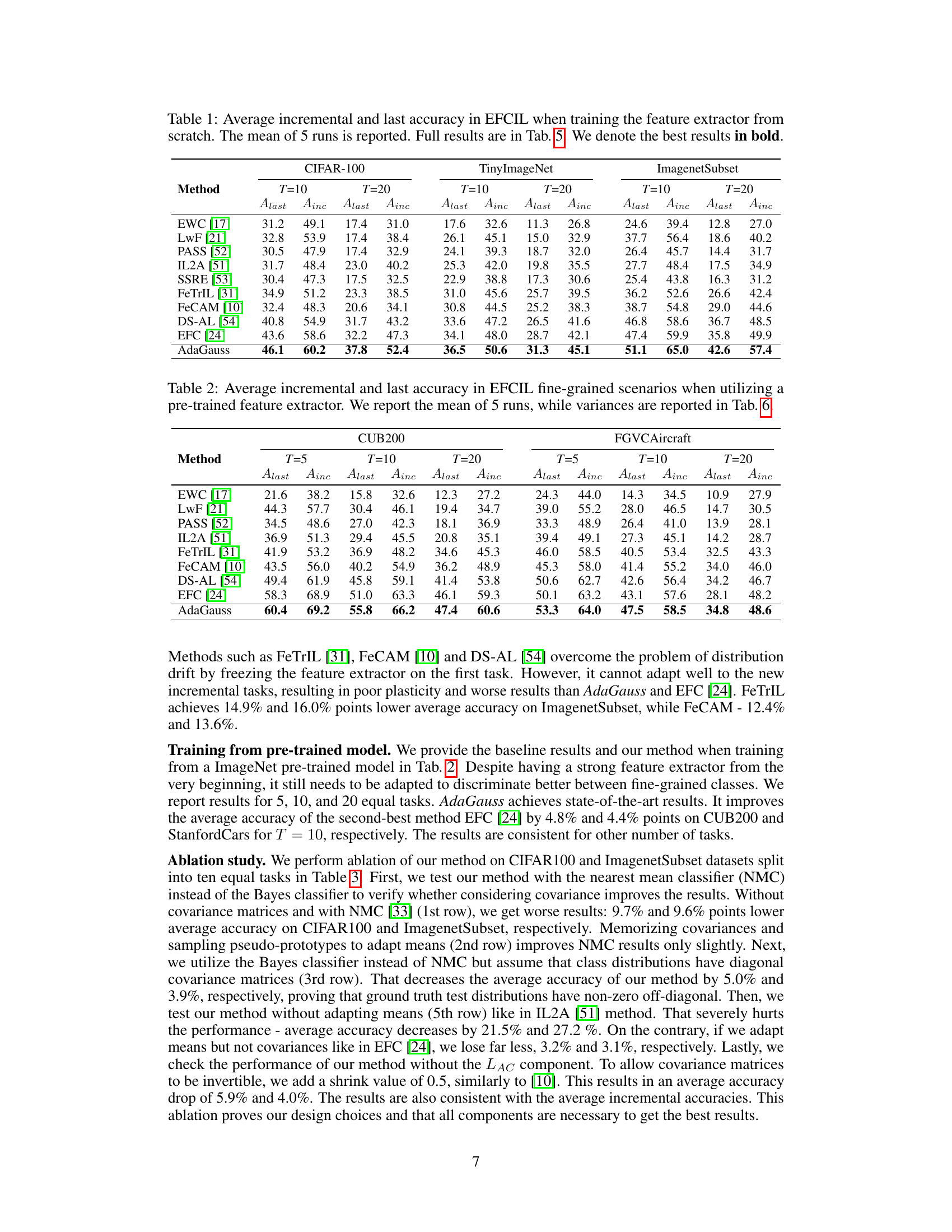
This table presents the average incremental and last accuracy achieved by different continual learning methods on three benchmark datasets (CIFAR-100, TinyImageNet, and ImagenetSubset). The results are obtained when training the model’s feature extractor from scratch, not using pre-trained weights. The table shows the performance for both 10 and 20 incremental tasks, reporting the average accuracy across all tasks (Ainc) and the accuracy after the last task (Alast). The best results for each dataset and task setting are highlighted in bold, providing a direct comparison of the AdaGauss method against several baselines.
In-depth insights#
Task-Recency Bias#
Task-recency bias, a significant challenge in continual learning, describes the phenomenon where a model disproportionately favors recently learned tasks. This is particularly problematic in exemplar-free class incremental learning (EFCIL), where past data is unavailable. The paper highlights that this bias arises from the dimensionality collapse of feature representations during training, leading to poorly conditioned covariance matrices for older tasks. This collapse causes issues with inverting covariance matrices needed for classification, thus exacerbating the recency bias. The proposed AdaGauss method directly addresses this by introducing an anti-collapse loss to maintain feature representation quality across all tasks, thus mitigating the bias and improving performance. Adapting covariance matrices across tasks, not just means, is another critical aspect of the proposed approach that further alleviates the bias.
AdaGauss Method#
The AdaGauss method tackles the challenges of adapting covariances and mitigating dimensionality collapse in Exemplar-Free Class Incremental Learning (EFCIL). It directly addresses the limitations of existing EFCIL methods that fail to adapt covariance matrices across incremental tasks, leading to inaccuracies and a task-recency bias. AdaGauss innovatively introduces an anti-collapse loss function to prevent the shrinking of covariance matrices, a common issue in deep learning that worsens in EFCIL settings. This ensures that the model retains sufficient information about older classes during subsequent training. Further, it employs feature distillation via a learnable projector network, improving the feature extractor’s representational strength and addressing the task-recency bias. By adapting both means and covariances of memorized class distributions, AdaGauss achieves state-of-the-art results on several benchmark datasets, showcasing its efficacy in handling the unique challenges of EFCIL. The approach is particularly notable for its simultaneous focus on covariance adaptation and dimensionality reduction, making it a robust solution for continual learning scenarios.
Covariance Adaptation#
Covariance adaptation in machine learning, especially within the context of continual learning, addresses the challenge of maintaining accurate representations of learned data distributions as new information arrives. Standard approaches often assume static covariances, which limits their effectiveness in dynamic environments where data characteristics evolve. Adapting covariances dynamically means recalculating the covariance matrices to reflect the changes in data distributions after each new task or batch of data. This is crucial because covariances capture the relationships between features, and these relationships are likely to shift over time. Failure to account for these changes leads to issues like task-recency bias (favoring recently seen data) and reduced accuracy. Efficient adaptation methods are needed to avoid computationally expensive recalculations of the entire covariance matrix for all classes. Incremental update strategies focusing on only the affected parts of the covariance matrix or low-rank approximations can significantly improve efficiency. The effectiveness of covariance adaptation is dependent on the quality of the underlying feature representations. This adaptation might be particularly beneficial when used in combination with approaches that address catastrophic forgetting.
Anti-Collapse Loss#
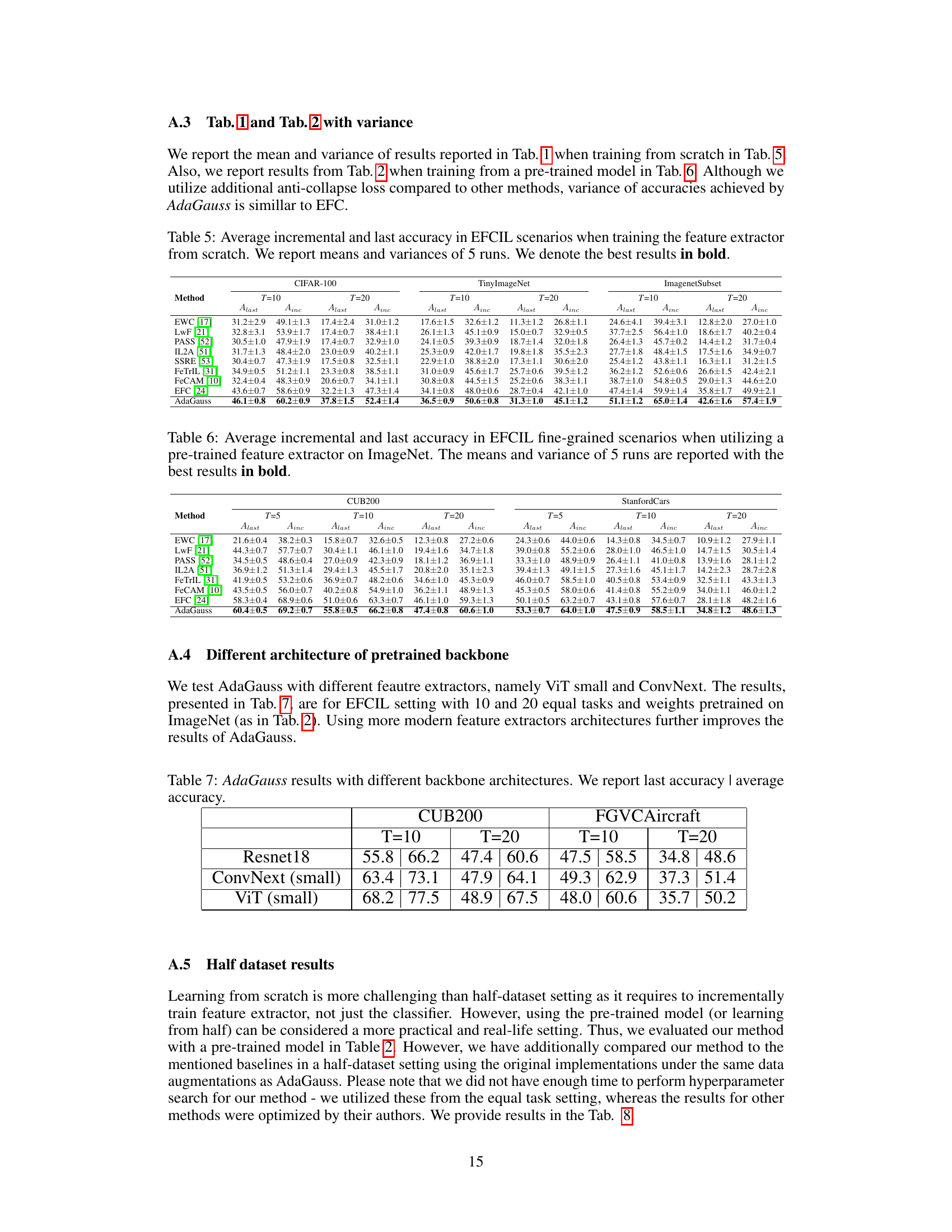
The concept of “Anti-Collapse Loss” in the context of continual learning addresses the critical issue of dimensionality collapse, a phenomenon where the feature representations learned by a neural network become increasingly concentrated in a lower-dimensional subspace during incremental training. This collapse hinders effective learning on new tasks, causing catastrophic forgetting and performance degradation, especially for previous tasks. The anti-collapse loss is designed to penalize this collapse, encouraging the network to maintain a diverse and informative representation across all learned tasks. This is achieved by explicitly optimizing the covariance matrix of the feature representations, promoting linearly independent features and preventing the concentration of variance into only a few dimensions. By incorporating this loss function into the training process, the model’s ability to retain information from past classes while adapting to new ones is significantly improved. This results in better generalization and improved resilience against catastrophic forgetting. The success of the anti-collapse loss depends on careful parameter tuning to balance the benefits of a rich representation against potential overfitting.
Future Directions#
Future research could explore several promising avenues. Improving the robustness of exemplar-free class incremental learning (EFCIL) methods to handle noisy or incomplete data is crucial. Investigating alternative approaches to knowledge distillation that better preserve information from previous tasks would be beneficial. Exploring different feature extraction techniques and their impact on the overall performance should also be a focus. Finally, developing better methods for assessing and mitigating the task-recency bias in EFCIL, potentially incorporating techniques from other areas of continual learning, would be valuable. The development of more efficient and scalable algorithms, especially for large-scale datasets, is also a key area for future work. In summary, advancing EFCIL requires addressing its robustness, improving knowledge transfer, exploring diverse feature representations, and mitigating the task recency bias.
More visual insights#
More on figures
The figure visualizes the effect of training on incremental tasks on the distribution of data points in latent space. When the feature extractor is frozen, the distributions of classes do not change, but they become inseparable. When it’s unfrozen, the distributions change, but existing methods do not adapt to those changes leading to classification errors. Therefore, a suitable continual learning method should adapt the mean and covariance of distributions to maintain valid decision boundaries.

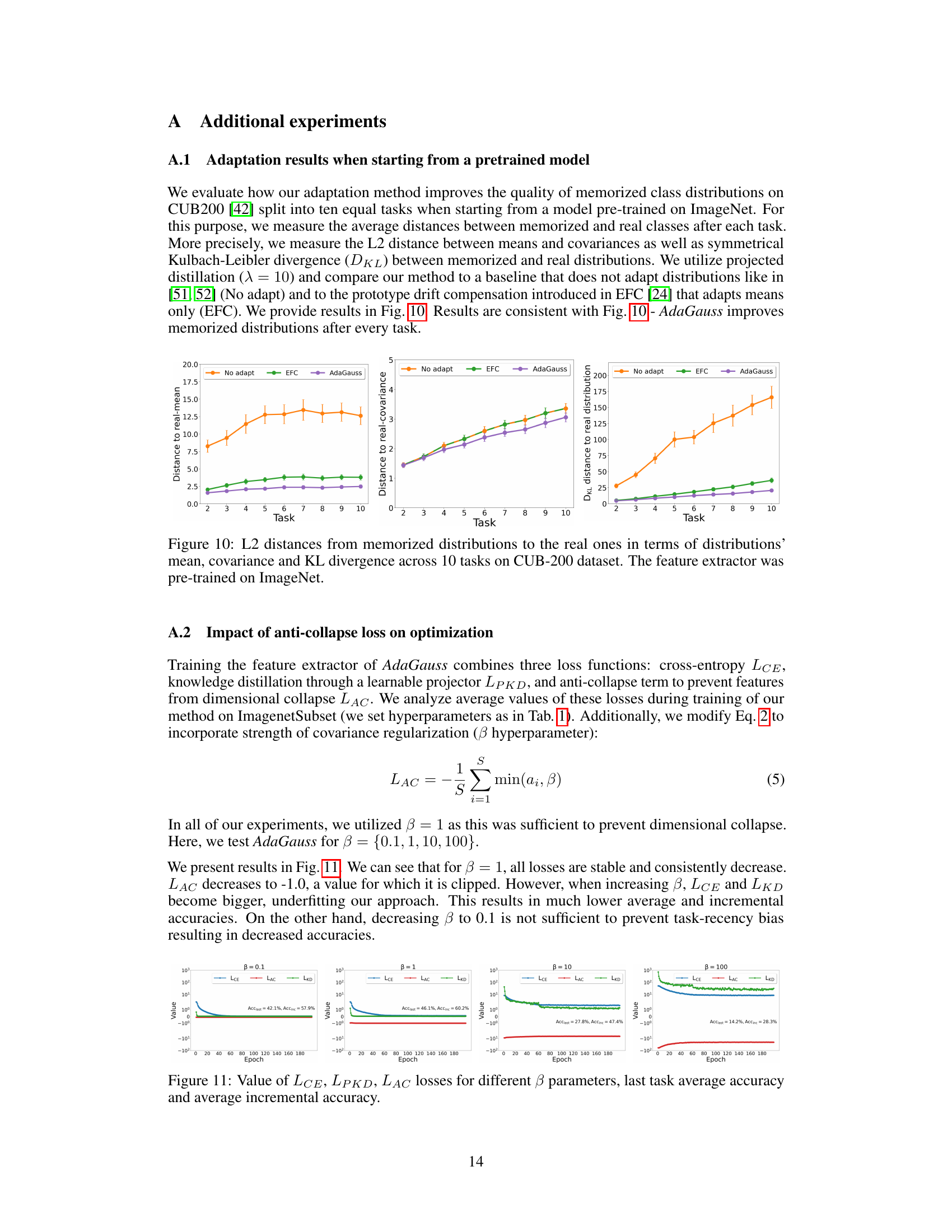
The figure visualizes the performance of three different methods (No adapt, EFC, and AdaGauss) in adapting Gaussian distributions across ten incremental tasks on the ImagenetSubset dataset. The three plots show the L2 distance between the memorized and real means, the L2 distance between the memorized and real covariance matrices, and the Kullback-Leibler (KL) divergence between the memorized and real distributions, respectively. AdaGauss consistently outperforms the other two methods, showcasing its effectiveness in adapting both the means and covariance matrices of Gaussian distributions, leading to more accurate representation of the learned classes and improved performance in continual learning.
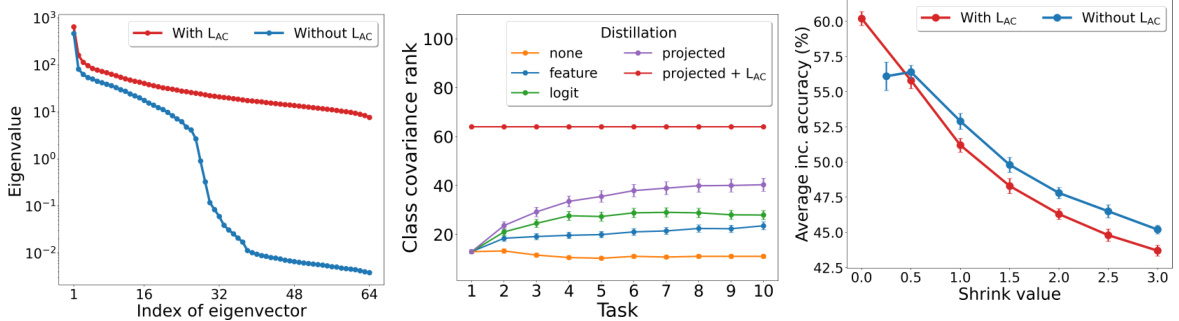
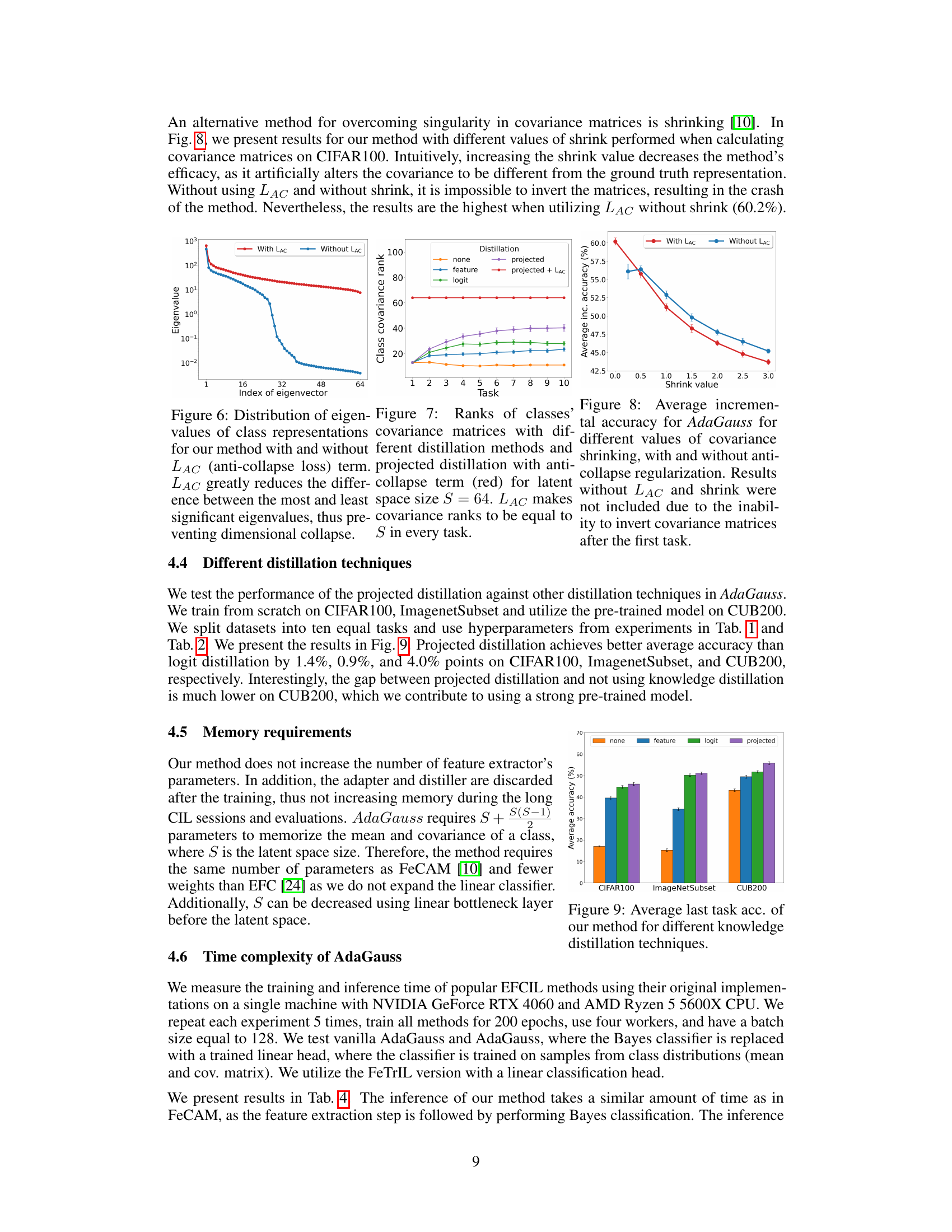
This figure visualizes the impact of the anti-collapse loss (LAC) on the distribution of eigenvalues of class representations. The left plot shows the eigenvalue distribution for the method with and without LAC. The plot shows that without LAC, there’s a large gap between the largest and smallest eigenvalues, indicating a dimensionality collapse, meaning the representations are concentrated in a small number of dimensions. With LAC, the distribution is significantly more uniform across all dimensions, demonstrating that LAC successfully prevents this collapse by ensuring more eigenvector contribute to representations.

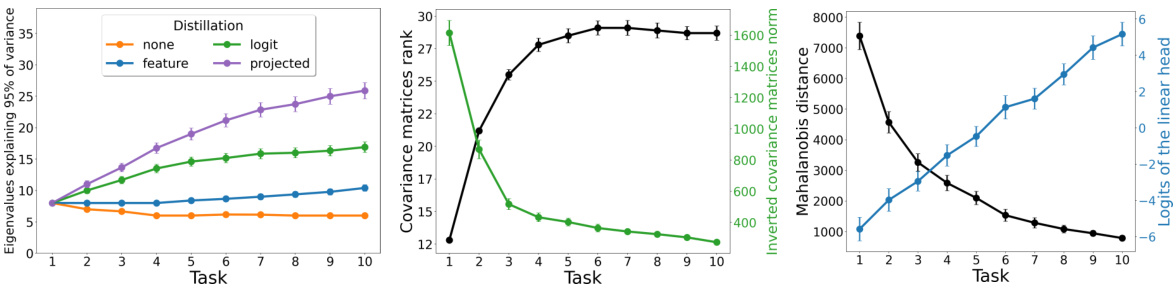
This figure visualizes how the representation strength of a ResNet18 model changes across ten incremental tasks of the ImageNetSubset dataset when trained with different knowledge distillation methods (none, feature, logit, projected). The x-axis represents the task number, and the y-axis shows the number of eigenvalues required to capture 95% of the total variance in the feature extractor’s output. The graph demonstrates that different knowledge distillation techniques lead to varying representational strengths throughout the training process, which has implications for the effectiveness of the method.
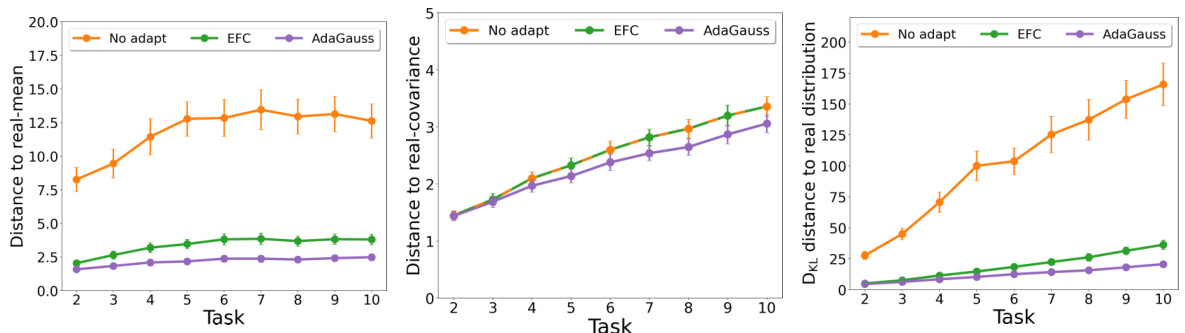
This figure visualizes the performance of AdaGauss in adapting class distributions compared to two other methods: one without adaptation and EFC (which only adapts means). The three graphs show the L2 distance between memorized and real means, the L2 distance between memorized and real covariance matrices, and the Kullback-Leibler (KL) divergence between memorized and real distributions, respectively, across ten incremental tasks on the ImagenetSubset dataset. The results demonstrate that AdaGauss significantly reduces the discrepancy between memorized and actual distributions compared to the other methods, highlighting its superior ability to adapt class distributions in continual learning.

This figure visualizes the effect of training a ResNet18 model sequentially on the ImagenetSubset dataset, divided into 10 tasks. The leftmost column shows the actual data points from past classes. The rest shows memorized distributions (how the model remembers the distributions) in the feature extractor’s latent space with different training approaches. Freezing the feature extractor maintains past distributions unchanged but results in class inseparability. Unfreezing it with no adaptation shows the shift in ground truth distributions, highlighting the need for adaptation of means and covariances (shown in the rightmost columns) to maintain accurate class boundaries.

The figure visualizes the effectiveness of AdaGauss in adapting class distributions compared to methods that don’t adapt (No adapt) and only adapt means (EFC). It shows the L2 distance between memorized and real class means, the L2 distance between memorized and real class covariances, and the Kullback-Leibler (KL) divergence between the distributions. AdaGauss consistently shows smaller distances, indicating better adaptation of class distributions across multiple tasks, demonstrating its superiority in handling distribution drift.
More on tables

This table presents the average incremental and last accuracy results for different continual learning methods on two fine-grained image classification datasets (CUB200 and FGVCAircraft). The experiments use a pre-trained feature extractor, highlighting the performance of each method when adapting to new tasks without access to previous data. The table shows results for different numbers of tasks (T=5, T=10, T=20), comparing the average accuracy (Ainc) and the accuracy on the last task (Alast).
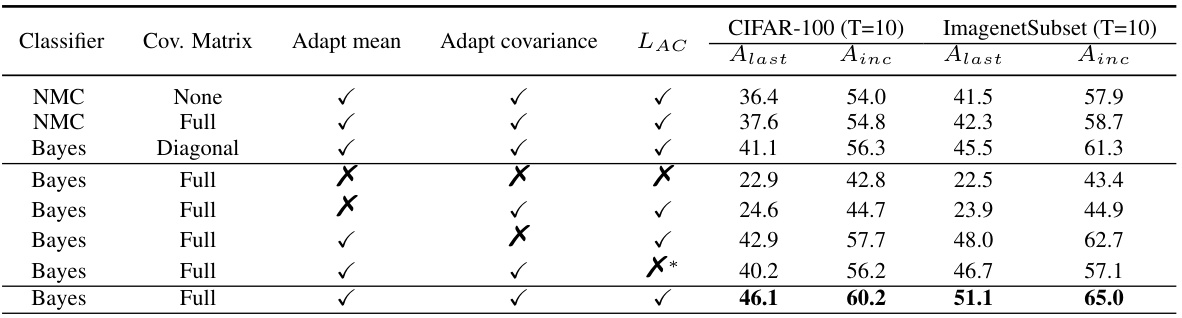
This table presents the ablation study of the AdaGauss method, showing the impact of different components on the performance. It demonstrates the necessity of adapting means and covariances, utilizing the Bayes classifier, and employing the anti-collapse loss for optimal results. The results are presented for CIFAR-100 and ImagenetSubset datasets with 10 tasks each.

This table presents the average incremental and last accuracy for different continual learning methods on CIFAR-100, TinyImageNet, and ImagenetSubset datasets when the feature extractor is trained from scratch. The results are shown for 10 and 20 tasks, each containing an equal number of classes. The best-performing methods are highlighted in bold, indicating the superior performance of AdaGauss, the proposed method, compared to other state-of-the-art approaches.

This table presents the average incremental and last accuracy achieved by different continual learning methods on three benchmark datasets (CIFAR-100, TinyImageNet, and ImageNetSubset) when training the feature extractor from scratch. The results are shown for two different numbers of tasks (T=10 and T=20). The best performing method for each metric and dataset is highlighted in bold. The table provides a summary of the performance, with more detailed results presented in Table 5.

This table presents the average incremental and last accuracy results for different continual learning methods on two fine-grained datasets (CUB200 and FGVCAircraft) when using a pre-trained feature extractor. The results are broken down by the number of tasks (T=5, T=10, T=20) and show the average performance across five runs. Variances for these results are provided in a separate table (Table 6). The table compares the performance of AdaGauss to several other state-of-the-art continual learning methods.

This table presents the results of the AdaGauss method using different backbone architectures (ResNet18, ConvNext (small), and ViT (small)) for the CUB200 and FGVCAircraft datasets. The experiments were conducted with 10 and 20 equal tasks, and the models used weights pre-trained on ImageNet. The table shows the last accuracy and average accuracy achieved by AdaGauss for each combination of dataset, task number, and architecture. This allows for a comparison of the performance of AdaGauss across different architectural choices.

This table presents the last accuracy and average accuracy for different continual learning methods on CIFAR100 and ImageNetSubset datasets when training is performed only on half of the data. It compares the performance of AdaGauss against other state-of-the-art methods in this specific setting.

This table presents the ablation study results on the impact of batch normalization on AdaGauss performance. It compares the last accuracy and average accuracy of AdaGauss when trained with no batch normalization, with frozen batch normalization, and with standard batch normalization (Resnet18). The results are shown for CIFAR100, ImageNetSubset, and CUB200 datasets.
Full paper#