↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Quantum Approximate Optimization Algorithm (QAOA) shows promise for combinatorial optimization, but its performance is limited by the circuit depth of current quantum computers. The required depth varies greatly depending on the problem, often exceeding the capacity of available hardware. This leads to QAOA underperforming even classical methods in many practical scenarios.
This paper introduces Mixer Generator Network (MG-Net), a deep learning model that addresses this challenge. MG-Net dynamically generates optimal mixer Hamiltonians, a crucial component of QAOA, that are tailored to both the specific problem and the maximum permissible circuit depth. The model’s design includes an estimator-generator structure and a two-stage training approach, which significantly reduces the need for a large training dataset. Experiments on Max-Cut and Ising models demonstrate MG-Net’s superior performance in terms of both approximation ratio and efficiency, showcasing its applicability to real-world problems.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles a major hurdle in practical quantum computing: the problem-specific circuit depth of Quantum Approximate Optimization Algorithm (QAOA). By introducing MG-Net, a deep learning framework that dynamically generates optimal mixer Hamiltonians tailored to specific problems and circuit depths, the research significantly advances the applicability of QAOA on current quantum hardware. It also opens exciting avenues for future research into the intersection of deep learning and quantum algorithm optimization.
Visual Insights#

This figure shows how the choice of Mixer Hamiltonian (HM) in the Quantum Approximate Optimization Algorithm (QAOA) impacts its performance. Panel (a) illustrates that a custom-designed HM can lead to a more direct and efficient path to the optimal solution than the standard HM, especially when the circuit depth (p) is limited. Panel (b) demonstrates that the effective dimension (deff) of the QAOA, which reflects the complexity of the algorithm, changes with increasing circuit depth (p), and this change is different depending on whether the HM uses correlated or independent parameters.
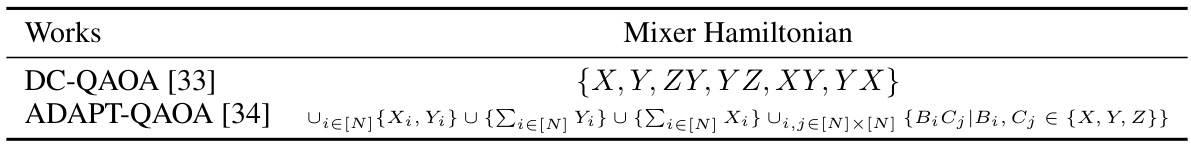
This table lists previous works that used the Pauli-Y operator, in addition to the Pauli-X operator, in the mixer Hamiltonian of the Quantum Approximate Optimization Algorithm (QAOA). The table shows that the use of the Pauli-Y operator is not new and has been explored in different contexts.
In-depth insights#
QAOA Convergence#
Analyzing QAOA convergence involves understanding how the algorithm’s performance changes with increasing circuit depth. Problem-specific behavior is a key aspect; some problems converge rapidly, while others require significantly more depth. The choice of mixer Hamiltonian plays a crucial role, influencing convergence speed and the algorithm’s ability to find good solutions. Theoretical analysis often uses tools like representation theory to explain convergence properties, relating them to symmetries in the problem Hamiltonian and the ansatz. Empirical studies via simulation or real quantum hardware provide valuable insights into the actual convergence behavior across various problem instances and circuit depths, highlighting the trade-off between performance and available resources. Parameter grouping strategies, within the mixer Hamiltonian, offer a potential avenue to improve convergence, but their effectiveness is problem-dependent. Ultimately, achieving a practical understanding of QAOA convergence necessitates both rigorous theoretical models and extensive empirical validation.
MG-Net Framework#
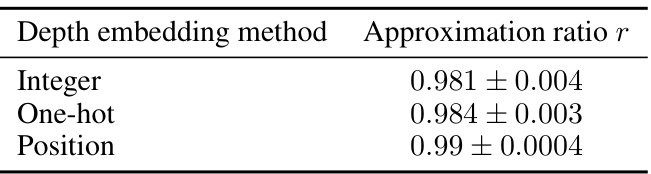
The MG-Net framework is presented as a novel deep learning approach to dynamically generate optimal mixer Hamiltonians for the Quantum Approximate Optimization Algorithm (QAOA). Its key innovation lies in addressing QAOA’s challenge of requiring problem-specific circuit depths that often exceed the capabilities of current quantum hardware. Instead of relying on pre-defined mixer Hamiltonians, MG-Net learns to tailor the Hamiltonian based on both the specific problem instance and the available circuit depth. This is achieved through a two-stage training process. First, a cost estimator is trained to predict QAOA’s performance given a problem and a mixer Hamiltonian; second, a mixer generator is trained to design Hamiltonians that minimize the estimated cost. The framework’s design incorporates a problem encoder to handle varied problem representations and a depth embedding to account for varying circuit depths. Finally, MG-Net’s ability to rapidly adapt to unseen problems and depths, evidenced by superior performance in simulations across various problems and qubit counts, showcases its potential for practical QAOA implementations on near-term quantum devices.
Mixer Hamiltonian#
The concept of the “Mixer Hamiltonian” is central to the Quantum Approximate Optimization Algorithm (QAOA). It’s a crucial component responsible for guiding the quantum system’s evolution towards the optimal solution. The paper delves into the intricate relationship between the mixer Hamiltonian, the problem’s structure, and the available circuit depth, highlighting that optimal mixer Hamiltonians are problem-specific and depth-dependent. A key contribution is the introduction of MG-Net, a deep learning framework designed to dynamically generate optimal mixer Hamiltonians tailored to specific problems and circuit depth constraints. This addresses the challenge of limited circuit depth in current quantum devices by adapting the mixer Hamiltonian. The theoretical analysis supports the design choices of MG-Net by demonstrating how parameter grouping within the mixer Hamiltonian can significantly impact convergence, leading to faster and more efficient optimization. MG-Net demonstrates superior performance in both approximation ratio and efficiency compared to traditional methods, showcasing the potential of learning-based approaches in customizing QAOA for practical applications.
Experimental Setup#
A well-defined Experimental Setup section is crucial for reproducibility and validation of research findings. It should detail all aspects of the experiment’s design and execution, allowing others to replicate the study and verify the results. Key aspects to include are dataset descriptions (size, source, characteristics, and preprocessing steps), model specifications (architecture, hyperparameters, and training procedures), and evaluation metrics (how performance was measured and any statistical significance tests used). Ambiguity should be avoided; clear, concise language and precise numerical values are essential. Any unusual or non-standard procedures should be carefully explained and justified. The experimental setup should also describe the computational resources used, such as hardware and software, ensuring transparency. Finally, discussing potential limitations or biases in the experimental setup, such as data imbalances or selection bias, is essential for a robust and credible research paper. A comprehensive approach in this section fosters trust and encourages future research by ensuring the study’s findings are verifiable and can be reliably built upon.
Future Research#
The paper’s ‘Future Research’ section would ideally address several key limitations. First, reducing the reliance on a labeled dataset for cost estimator training is crucial. Exploring unsupervised or self-supervised methods would significantly enhance scalability and reduce data collection costs. Second, extending MG-Net’s applicability beyond QAOA to other VQAs would broaden its impact. This requires investigating how the core principles of dynamic mixer Hamiltonian generation can be adapted to the unique characteristics of different VQAs. Third, enhancing robustness to noise and imperfections in practical quantum hardware is vital for real-world applicability. This necessitates exploring noise-mitigation techniques and developing MG-Net variants that can operate effectively under noisy conditions. Finally, a more thorough theoretical investigation into the convergence properties of MG-Net is needed to complement the empirical results. Such investigation could reveal valuable insights into optimal architectural choices and training strategies, possibly leading to even faster convergence and higher approximation ratios.
More visual insights#
More on figures

This figure illustrates the framework of the Mixer Generator Network (MG-Net). The training phase involves two stages: first training a cost estimator to predict QAOA performance, then training a mixer generator (unsupervised) to produce optimal mixer Hamiltonians that minimize the cost estimator’s output. The inference phase uses only the trained mixer generator to produce a mixer Hamiltonian for a given problem and circuit depth, which is then used by a QAOA solver.
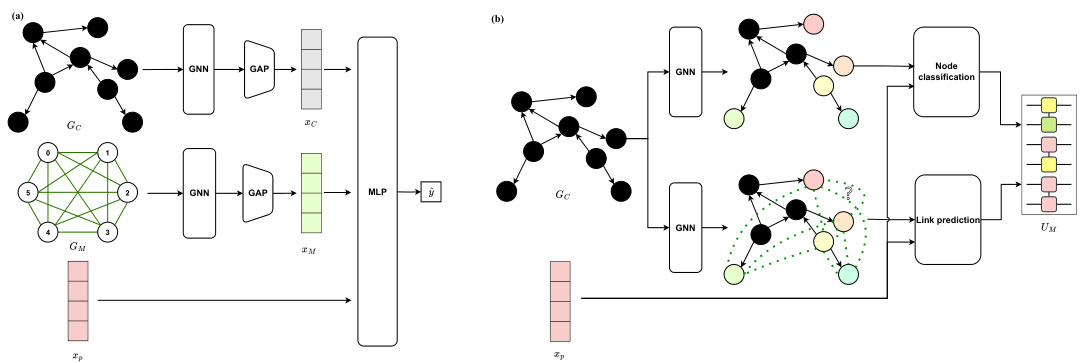
This figure illustrates the framework of the Mixer Generator Network (MG-Net). The training phase involves two stages: 1) training a cost estimator to predict QAOA performance given problem parameters, circuit depth, and a mixer Hamiltonian, and 2) training a mixer generator (with the cost estimator fixed) to produce an optimal mixer Hamiltonian that minimizes the cost. The inference phase shows how, given a problem and circuit depth, the MG-Net generates a mixer Hamiltonian which is then used by a QAOA solver to find a solution.
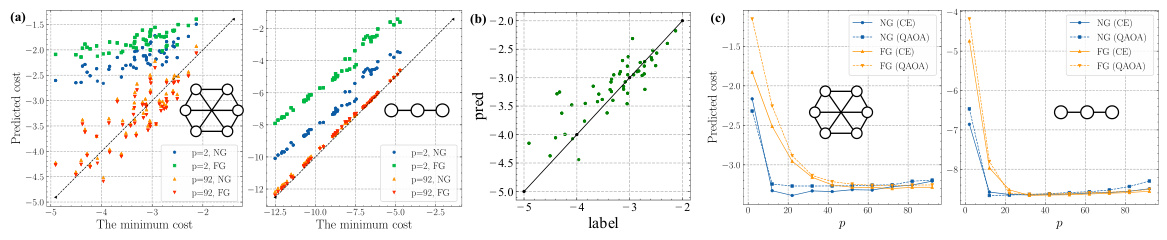
This figure demonstrates the performance of the cost estimator in MG-Net. Panel (a) shows the correlation between the estimated cost and the actual minimum cost achieved by QAOA for Max-Cut and TFIM problems, demonstrating the accuracy of the estimator. Panel (b) extends this analysis to a larger set of mixer operators, showing continued accuracy. Panel (c) shows how the achievable cost changes with varying circuit depth (p) for both problems and both fully grouped (FG) and non-grouped (NG) parameter strategies, highlighting the estimator’s ability to predict QAOA performance at different depths and parameter settings.

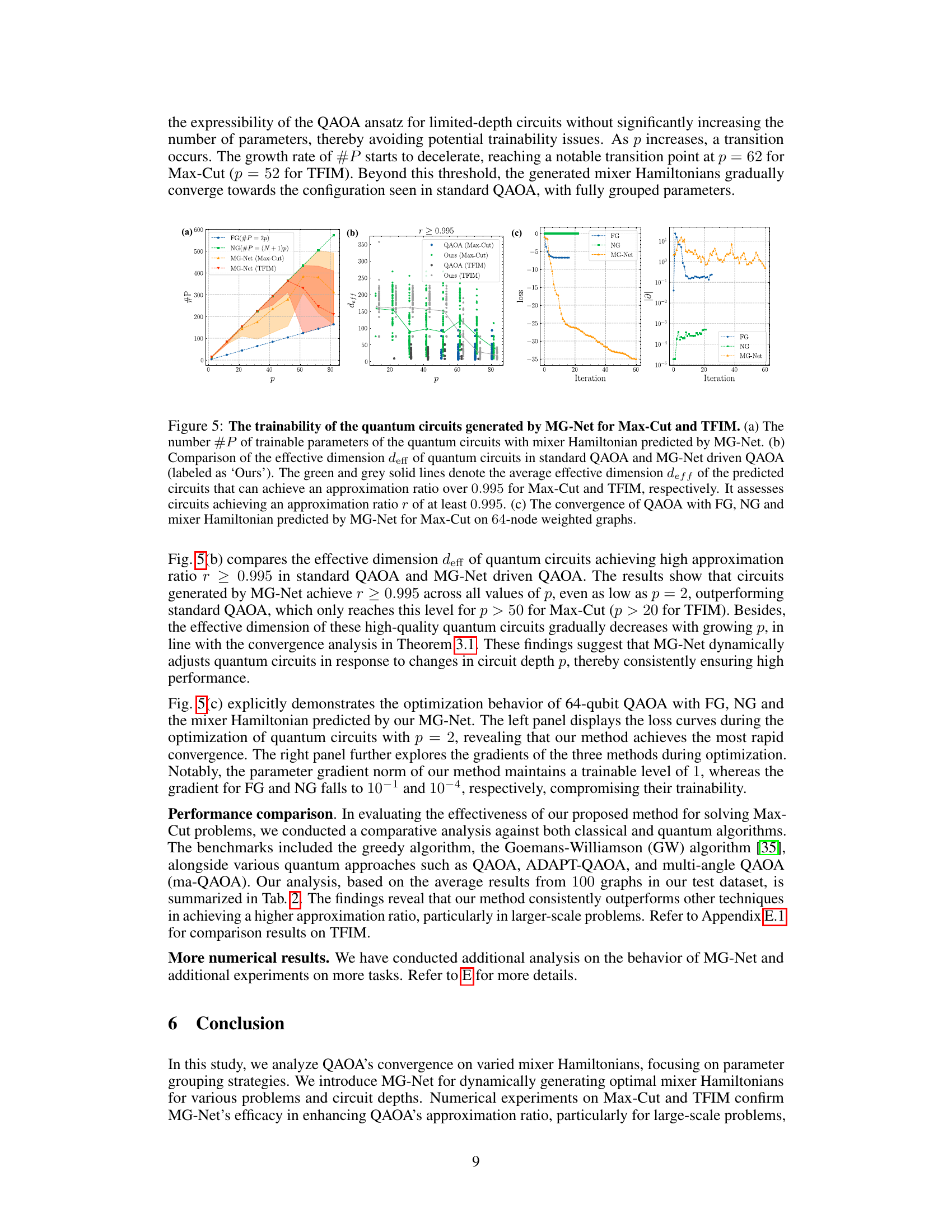
This figure compares the trainability of quantum circuits generated by MG-Net and standard QAOA for Max-Cut and TFIM problems. Subfigure (a) shows the number of trainable parameters (#P) for each method as a function of circuit depth (p). Subfigure (b) compares the effective dimension (deff) required to achieve a high approximation ratio (r ≥ 0.995). Subfigure (c) shows the convergence behavior of the different methods for a Max-Cut problem with 64 nodes.
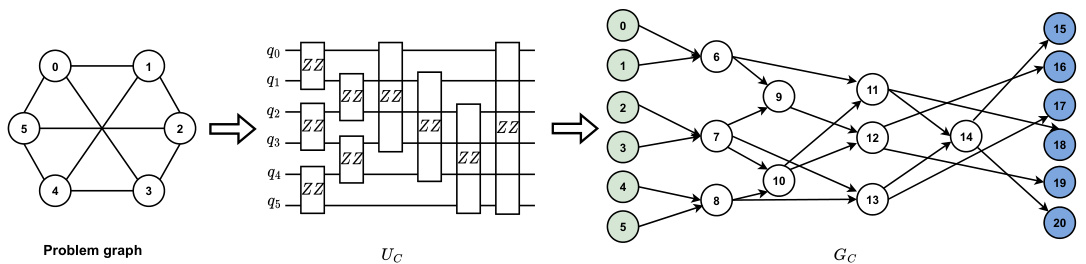
This figure illustrates the process of encoding a problem graph into a directed acyclic graph (DAG) representation for use in the MG-Net model. The problem graph, representing the combinatorial optimization problem, is first converted into a quantum circuit (Uc) where each edge in the problem graph corresponds to a two-qubit gate in the quantum circuit. This quantum circuit is then represented as a DAG (Gc), where each node represents a two-qubit gate and the edges represent the sequential order of gate execution. The resulting DAG Gc serves as a structured input for the MG-Net model.
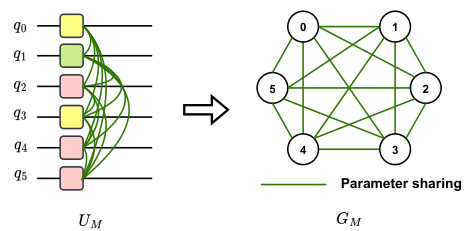
This figure illustrates how the mixer Hamiltonian is encoded as a graph for the MG-Net model. Each node in the graph represents a qubit, with the node’s features indicating the type of Pauli operator (X or Y) applied to that qubit. The edges of the graph represent the parameter sharing strategy. If two qubits share the same trainable parameter (i.e., they are in the same parameter group), an edge connects their corresponding nodes. This graph representation allows the MG-Net to learn the optimal parameter grouping and operator types for different problems and circuit depths.
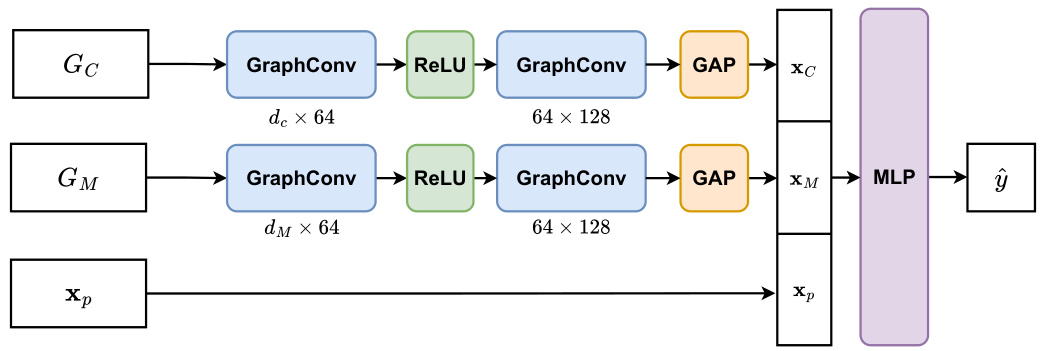
This figure shows the architecture of the cost estimator component of the MG-Net model. It consists of three input branches: one for the problem graph (Gc), one for the mixer Hamiltonian graph (GM), and one for the depth embedding (xp). Each branch uses two layers of graph convolutions followed by ReLU activation and global average pooling (GAP) to extract features. These features are then concatenated and fed into a multi-layer perceptron (MLP) to predict the minimum cost (ŷ) of the QAOA algorithm.
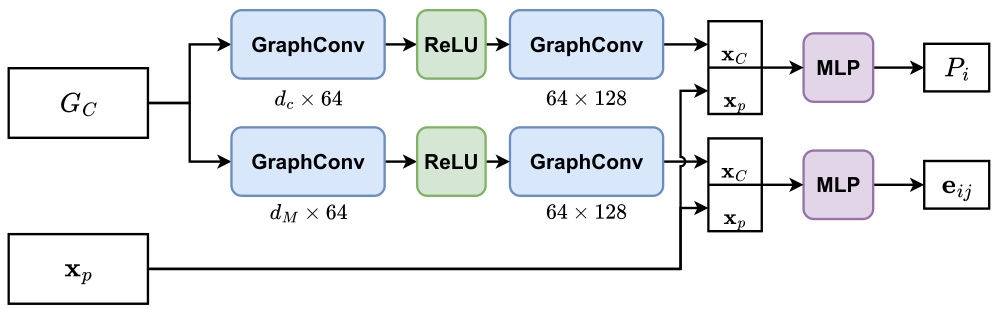
This figure shows the architecture of the cost estimator and mixer generator in MG-Net. The cost estimator takes problem, mixer Hamiltonian and circuit depth as input and estimates the QAOA cost. The mixer generator is divided into two parts that generate operator type and parameter grouping.

This figure shows two types of graphs used in the experiments. The left graph is an asymmetric graph, while the right graph is a 2D TFIM graph. These graphs are used to evaluate the performance of the proposed MG-Net model. The asymmetric graph is used to test the generalizability of the model to non-regular graphs, while the 2D TFIM graph is used to test the model on a more structured graph.
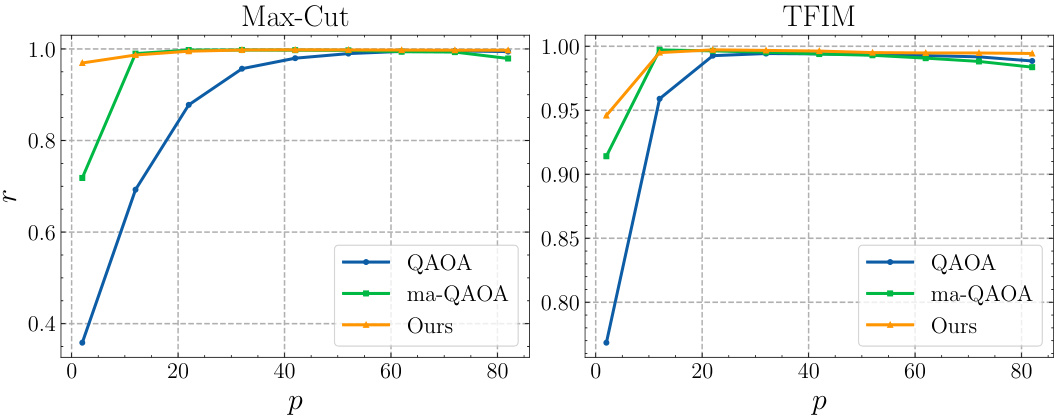
This figure compares the approximation ratios achieved by three different methods (standard QAOA, multi-angle QAOA, and the proposed MG-Net method) for solving Max-Cut and TFIM problems. The x-axis represents the circuit depth (p), and the y-axis represents the approximation ratio (r). The plot shows that the proposed method consistently achieves a higher approximation ratio than the other two methods across different circuit depths. It also shows that the performance of ma-QAOA decreases for larger values of p, suggesting potential over-parameterization issues, whereas MG-Net maintains high performance.

This figure compares the convergence speed of three different QAOA methods (standard QAOA, multi-angle QAOA, and the proposed MG-Net method) for solving Max-Cut and TFIM problems. The convergence is shown for different circuit depths (p = 4, 6, 8, 10). It demonstrates that MG-Net achieves a lower loss value in fewer iterations compared to the other two methods, highlighting its superior efficiency and convergence performance.
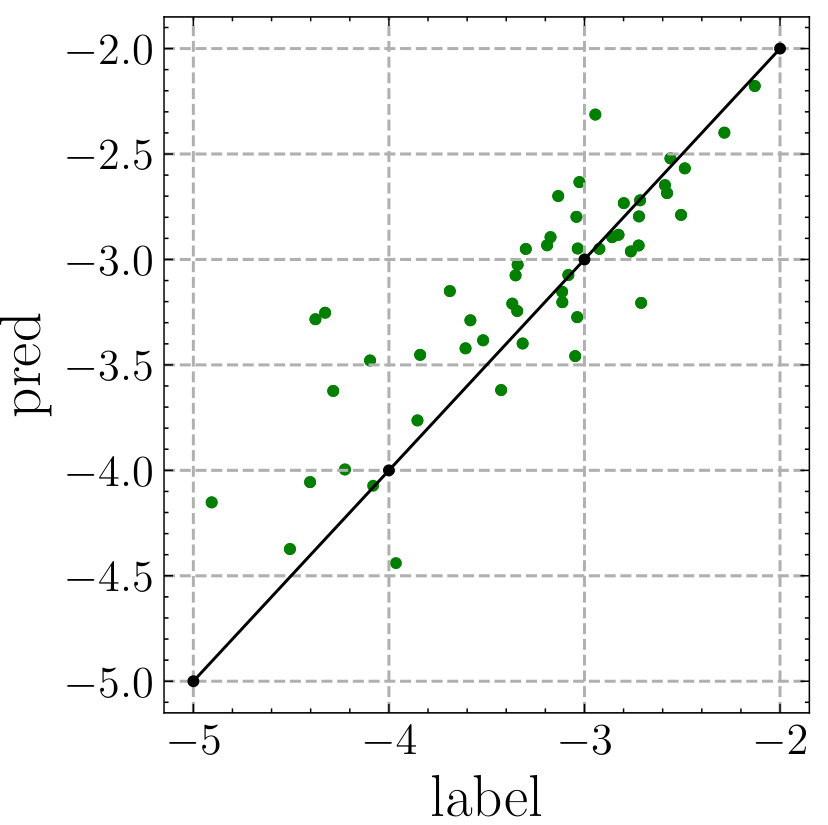
This figure shows the performance of the cost estimator in predicting the minimum cost achievable by QAOA for different problems, circuit depths, and mixer Hamiltonians. It demonstrates a strong correlation between estimated and actual minimum costs, even with more complex Hamiltonians. It also shows how the achievable cost changes with varying circuit depth, aligning with theoretical analysis of QAOA convergence.
More on tables
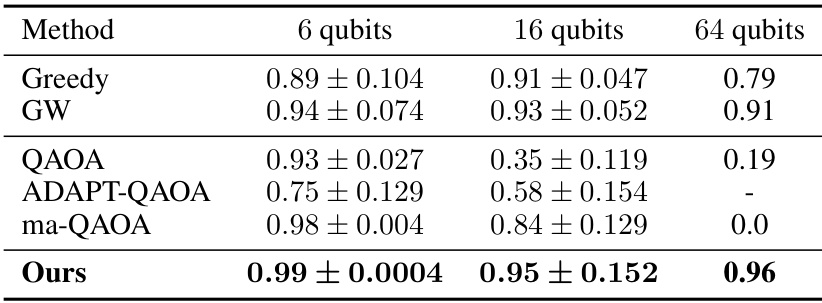
This table compares the approximation ratios achieved by different methods for solving the Max-Cut problem. The methods compared include Greedy, Goemans-Williamson (GW), QAOA, ADAPT-QAOA, multi-angle QAOA (ma-QAOA), and the proposed MG-Net method. Results are presented for graphs with 6, 16, and 64 qubits. The table shows that the proposed method generally achieves higher approximation ratios, particularly for larger graph sizes.

This table compares the approximation ratios achieved by different methods (Greedy, Goemans-Williamson, QAOA, ADAPT-QAOA, ma-QAOA, and the proposed MG-Net method) for solving the Max-Cut problem on graphs with 6, 16, and 64 qubits. It showcases the superior performance of the MG-Net method, especially for larger graphs.
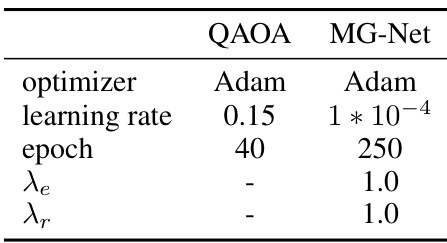
This table shows the hyperparameters used for training both the MG-Net model and the QAOA circuit. It lists the optimizer (Adam for both), learning rates, number of epochs, and weighting parameters for the loss function (λe and λr). The differing parameters highlight the different optimization strategies used for each.

This table compares the approximation ratio (r) achieved by different methods for the Transverse-field Ising Model (TFIM) problem. The methods compared are QAOA, ADAPT-QAOA, multi-angle QAOA (ma-QAOA), and the proposed MG-Net method. The results are shown for both 6-qubit and 16-qubit TFIM instances. The approximation ratio is a measure of the algorithm’s performance, with higher values indicating better performance.
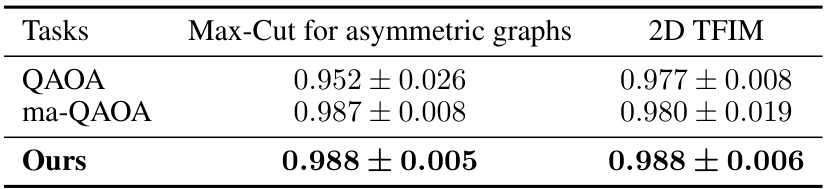
This table compares the approximation ratios achieved by different methods (Greedy, Goemans-Williamson, QAOA, ADAPT-QAOA, ma-QAOA, and the proposed MG-Net method) for the Max-Cut problem on graphs with varying numbers of qubits (6, 16, and 64). The results show the mean approximation ratio and standard deviation achieved by each method. The proposed method shows consistently higher approximation ratios, especially as the number of qubits increases.
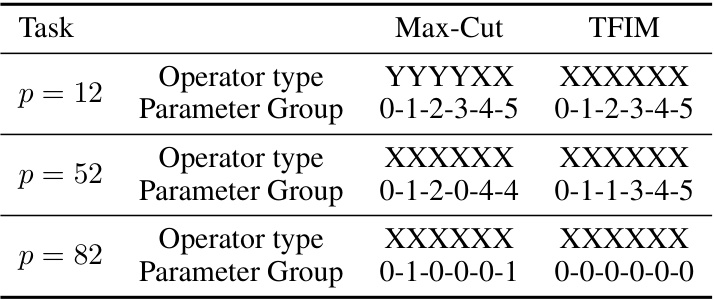
This table shows the operator types and parameter groups generated by the MG-Net model for different circuit depths (p=12, 52, 82) and tasks (Max-Cut and TFIM). It illustrates how the model dynamically adjusts the mixer Hamiltonian by changing the operator types and grouping parameters according to the problem and circuit depth.
This table presents a comparison of the approximation ratios achieved by different methods for solving the Max-Cut problem. The methods compared include the greedy algorithm, the Goemans-Williamson (GW) algorithm, QAOA, ADAPT-QAOA, multi-angle QAOA (ma-QAOA), and the proposed MG-Net method. The results are shown for graphs with 6, 16, and 64 qubits. The table highlights the superior performance of the MG-Net method, especially for larger-scale problems.
Full paper#