FIDE: Frequency-Inflated Conditional Diffusion Model for Extreme-Aware Time Series Generation

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on time series generation and extreme value analysis. It addresses a critical limitation of existing diffusion models, improving the accuracy of extreme event prediction. The proposed method opens avenues for more robust risk management, scenario planning, and anomaly detection in various applications.

Visual Insights

#

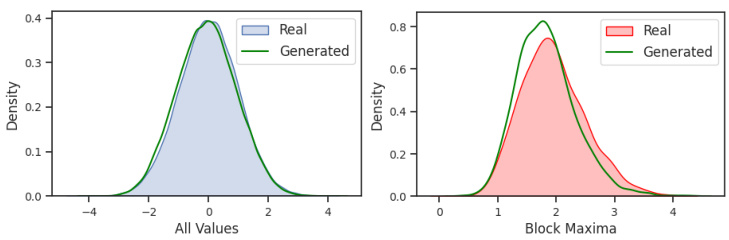
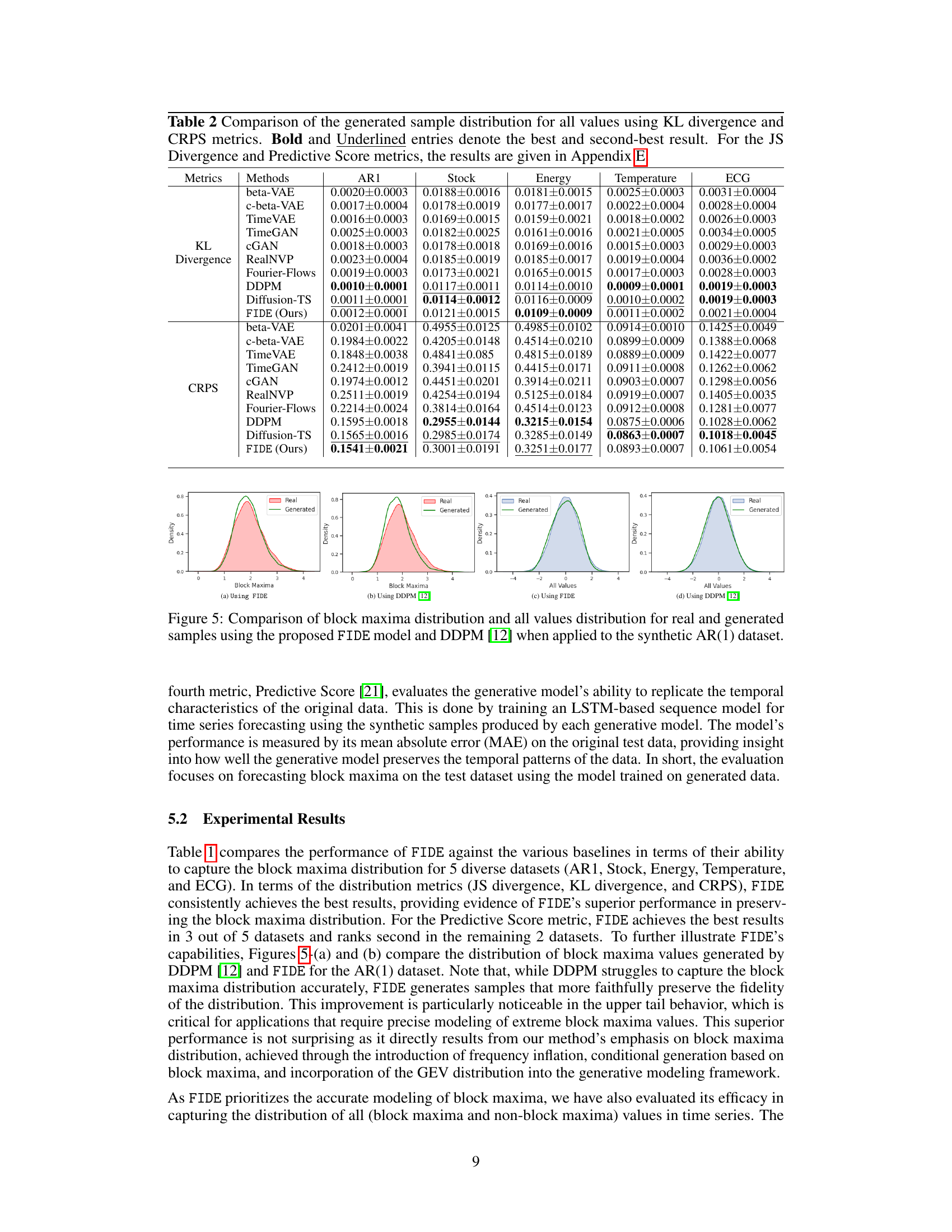
This figure compares the distributions of all values and block maxima values obtained from real and generated time series data using the Denoising Diffusion Probabilistic Model (DDPM). The left panel shows that DDPM effectively captures the distribution of all values in the synthetic AR(1) dataset. However, the right panel reveals that DDPM struggles to preserve the distribution of block maxima values when the generated time series is partitioned into disjoint time windows. This illustrates the difficulty of modeling the distribution of block maxima using existing diffusion models.

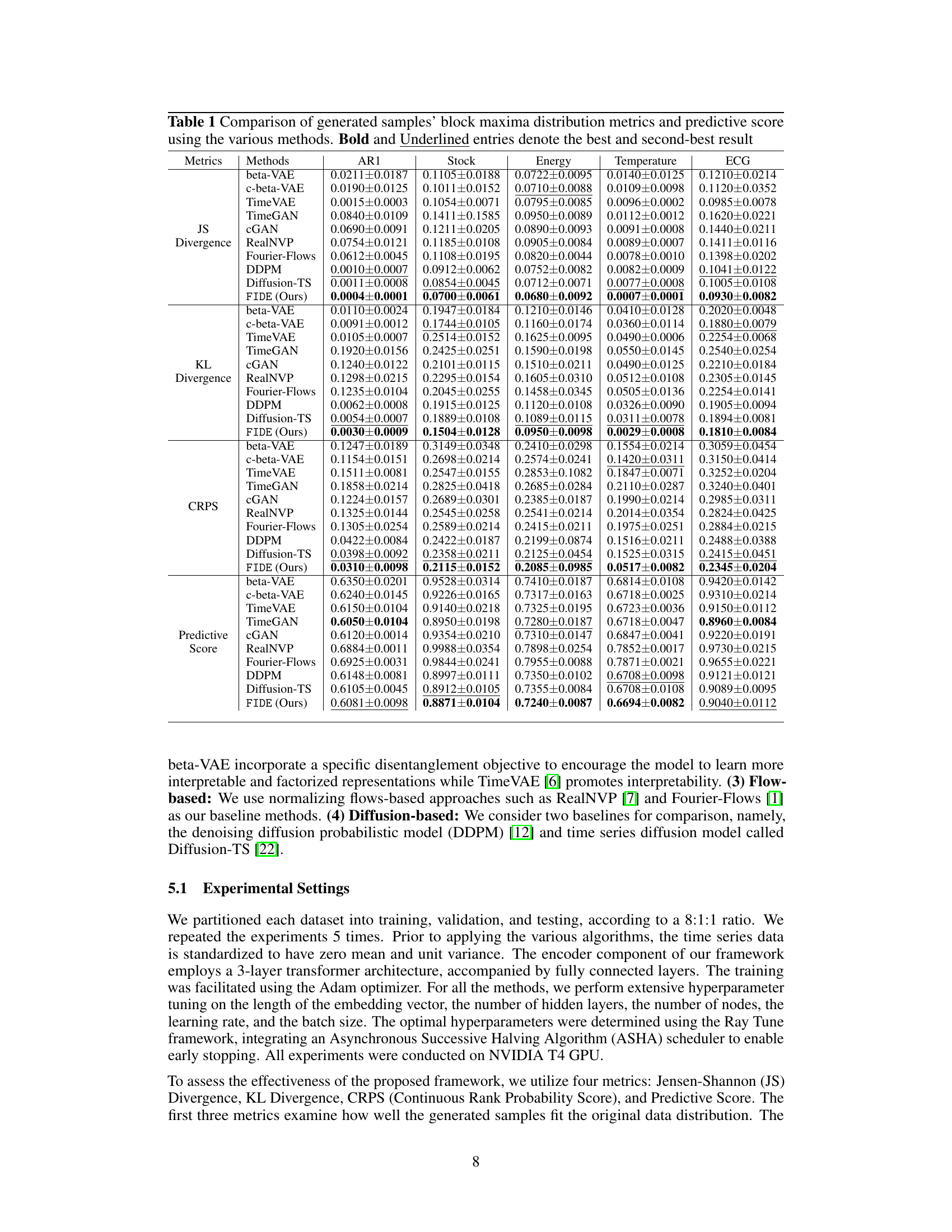
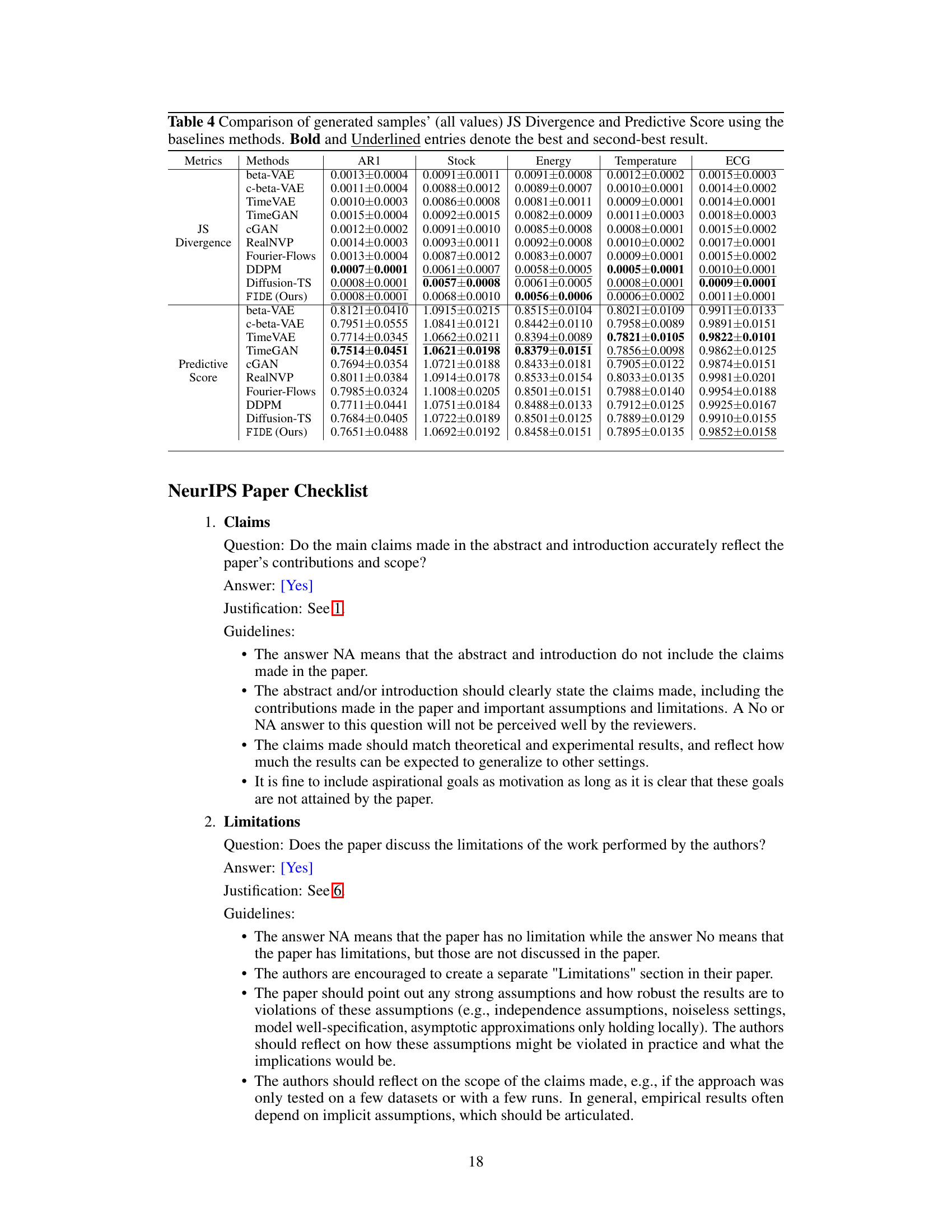
This table compares the performance of the proposed FIDE model against several baseline methods across five different datasets (AR1, Stock, Energy, Temperature, ECG). The comparison uses several metrics to evaluate the models’ ability to capture both the overall data distribution and the distribution of block maxima values. These metrics include the Jensen-Shannon (JS) divergence, Kullback-Leibler (KL) divergence, Continuous Ranked Probability Score (CRPS), and Predictive Score. The best and second-best performing models for each metric and dataset are highlighted.

In-depth insights

#

Extreme Value Focus

#

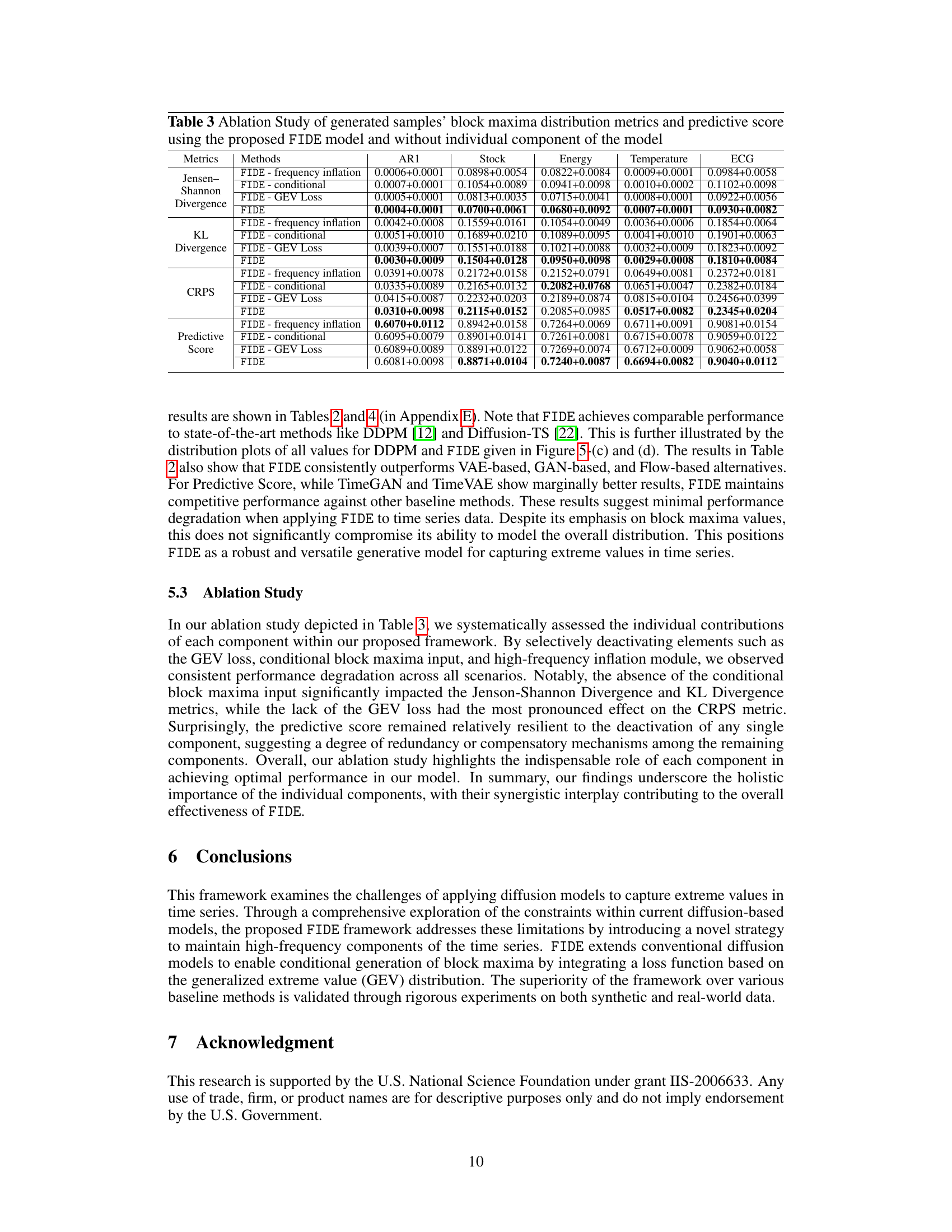
The research paper focuses on enhancing the modeling of extreme values in time series data using generative AI. Traditional methods often fail to adequately capture these rare events. The paper highlights the importance of high-frequency components in accurately reproducing extreme values, as they are strongly associated with abrupt temporal changes. A novel approach involving high-frequency inflation is introduced to prevent the premature fade-out of extreme values during the generation process. The use of a conditional diffusion model allows for generating samples conditioned on block maxima (the highest value within a time window), further improving accuracy. By incorporating the Generalized Extreme Value (GEV) distribution, the model ensures fidelity to both block maxima and the overall distribution. This focus on extremes makes the approach particularly suitable for applications needing robust risk management and scenario planning. The effectiveness is demonstrated through extensive experiments, showcasing significant improvements compared to traditional techniques.

High-Freq Inflation

#

The concept of ‘High-Freq Inflation’ in the context of time series generation using diffusion models is a crucial innovation to address the challenge of preserving extreme values. Standard diffusion models often prematurely attenuate high-frequency components, leading to the loss of important information associated with abrupt changes and extreme events. This method directly counteracts this issue by strategically inflating the high-frequency components in the frequency domain. This inflation ensures that the block maxima values, typically associated with these high-frequency signals, persist through the noise-addition process, thereby improving the model’s ability to accurately represent extreme events. The effectiveness of this technique hinges on its ability to balance the preservation of extreme values with the overall fidelity of the data distribution. It’s a carefully calibrated approach aimed at making diffusion models more robust and suitable for applications where modeling extreme events is paramount.

Conditional Diffusion

#

Conditional diffusion models are a powerful class of generative models that have shown remarkable success in various domains. They extend the basic diffusion process by incorporating conditioning information, enabling the generation of samples that satisfy specific constraints. This conditioning is crucial for controlling the generation process and ensuring that the output aligns with desired properties. The approach is particularly useful for time series generation because it allows modeling of dependencies and the incorporation of external factors. A key aspect of conditional diffusion is its flexibility in choosing the conditioning mechanism. It can range from simple constraints such as enforcing specific values at certain time points to more complex approaches that leverage external data or learned representations. Choosing the appropriate conditioning strategy is vital for balancing the quality and controllability of the generated samples. While conditional diffusion offers significant advantages, it also presents challenges. For example, the complexity of the conditioning mechanism can significantly impact computational cost and training stability. Moreover, optimizing the balance between fidelity to the conditioning information and the generation of diverse samples can be difficult. Future research may explore novel conditioning strategies, efficient architectures, and theoretical analysis to further advance this rapidly developing area of generative modeling.

GEV Distribution

#

The Generalized Extreme Value (GEV) distribution plays a crucial role in the paper by providing a robust framework for modeling the distribution of block maxima in time series data. The GEV’s ability to capture extreme values accurately is essential for enhancing the fidelity of the generative model, ensuring that the generated time series closely reflects the statistical properties of the original data. By incorporating the GEV distribution into the loss function, the model is explicitly trained to reproduce not only the overall data distribution but also the tail behavior. This approach directly addresses a key limitation of traditional diffusion models, which frequently fail to accurately capture extreme values. This focus on the GEV distribution is a significant contribution of the research, resulting in a generative model capable of realistically simulating both common and extreme events within the time series. The use of GEV ensures the model’s accurate representation of block maxima which is critical in several applications like risk management and scenario planning. The integration of the GEV distribution therefore significantly improves the quality and reliability of the generated time series.

FIDE Framework

#

The FIDE framework introduces a novel approach to time series generation by addressing the limitations of existing diffusion models in capturing extreme values. High-frequency component inflation strategically boosts the persistence of crucial high-frequency signals associated with extreme events, preventing their premature attenuation during the diffusion process. The framework further incorporates a conditional generation mechanism, conditioning the model on observed block maxima to enhance the model’s ability to capture the tail distribution. Finally, the integration of the Generalized Extreme Value (GEV) distribution into the loss function ensures the generated time series accurately reflects both the overall data distribution and the distribution of extreme values. This multifaceted approach leads to a more realistic and accurate time series generation, especially regarding extreme events. The combination of high-frequency inflation, conditional generation, and GEV regularization is key to FIDE’s superior performance, showcasing its potential for advancing generative AI in various applications requiring accurate extreme event modeling.

More visual insights

#

More on figures

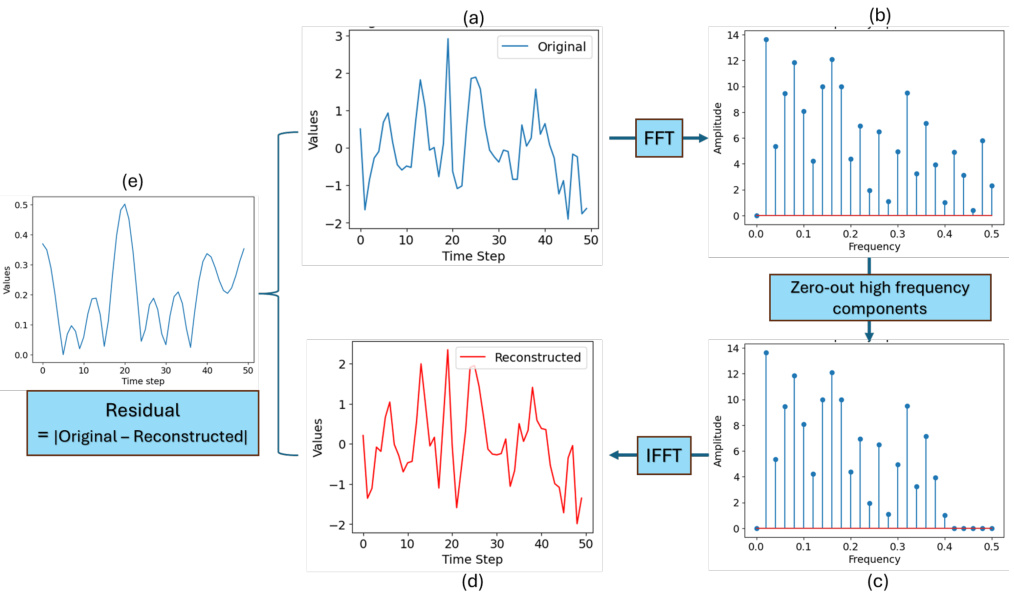
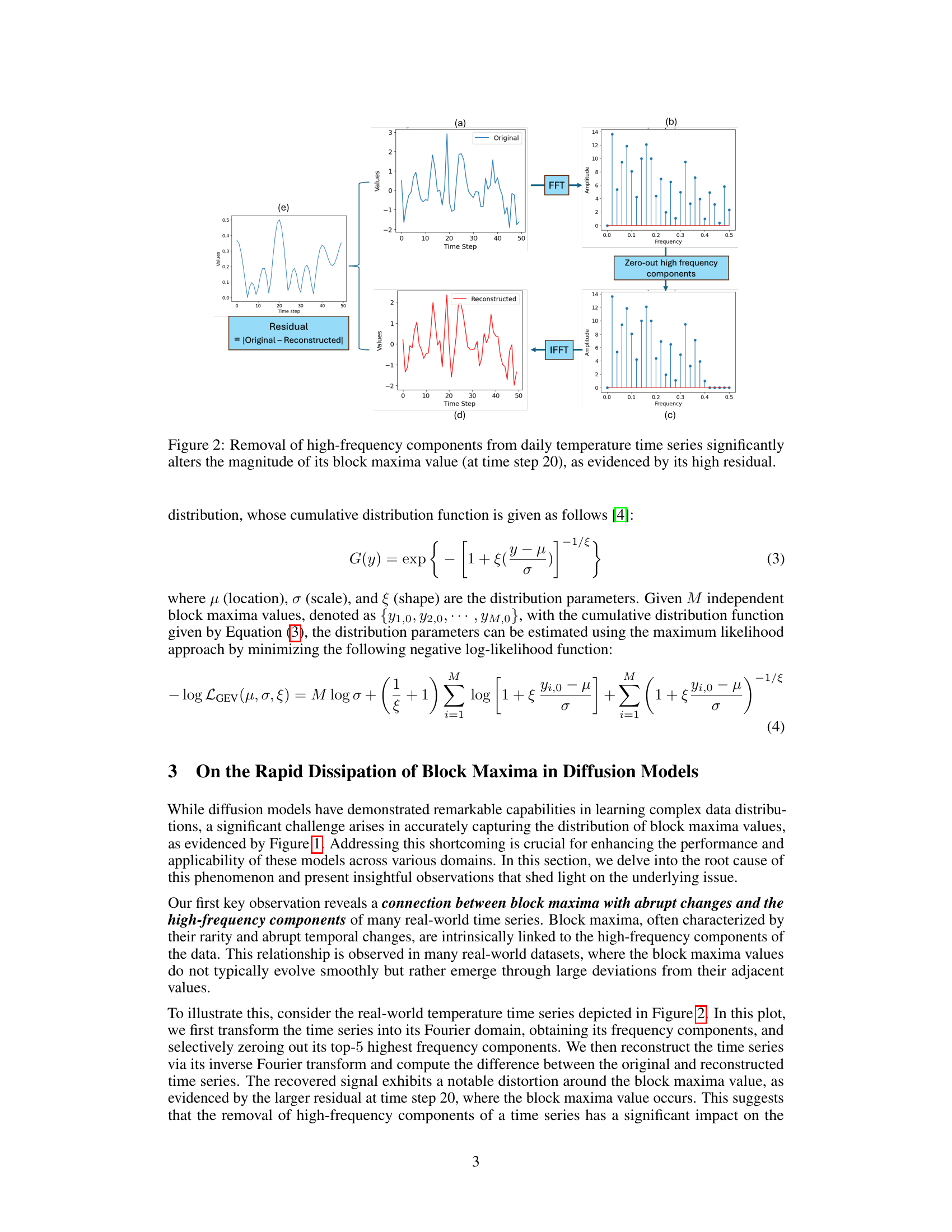
This figure demonstrates the impact of removing high-frequency components on the block maxima of a daily temperature time series. Subfigure (a) shows the original time series. (b) displays the Fast Fourier Transform (FFT) of the time series, showing the frequency components. The high-frequency components are then zeroed out, and an Inverse Fast Fourier Transform (IFFT) is applied to reconstruct the time series, shown in (d). The residual or difference between the original and reconstructed time series is shown in (e), clearly indicating that the removal of high-frequency components significantly alters the block maxima value at time step 20. This highlights the strong association between high-frequency components and abrupt changes in block maxima values.

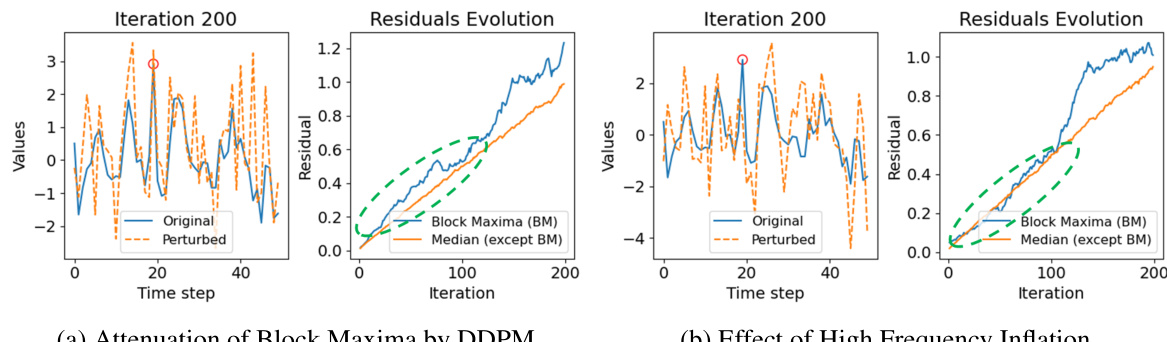
This figure compares the impact of noise addition (as done in standard DDPM) versus the proposed high-frequency inflation on the block maxima of generated time series samples. The left panel shows the attenuation of block maxima by DDPM, while the right shows the effect of high-frequency inflation strategy. The top row displays the original and perturbed time series. The bottom row shows how the residuals (difference between original and perturbed series) evolve over iterations. High-frequency inflation is designed to prevent the premature decay of high-frequency components (which are linked to block maxima) during the diffusion process. The figure illustrates that high-frequency inflation better preserves the block maxima values.

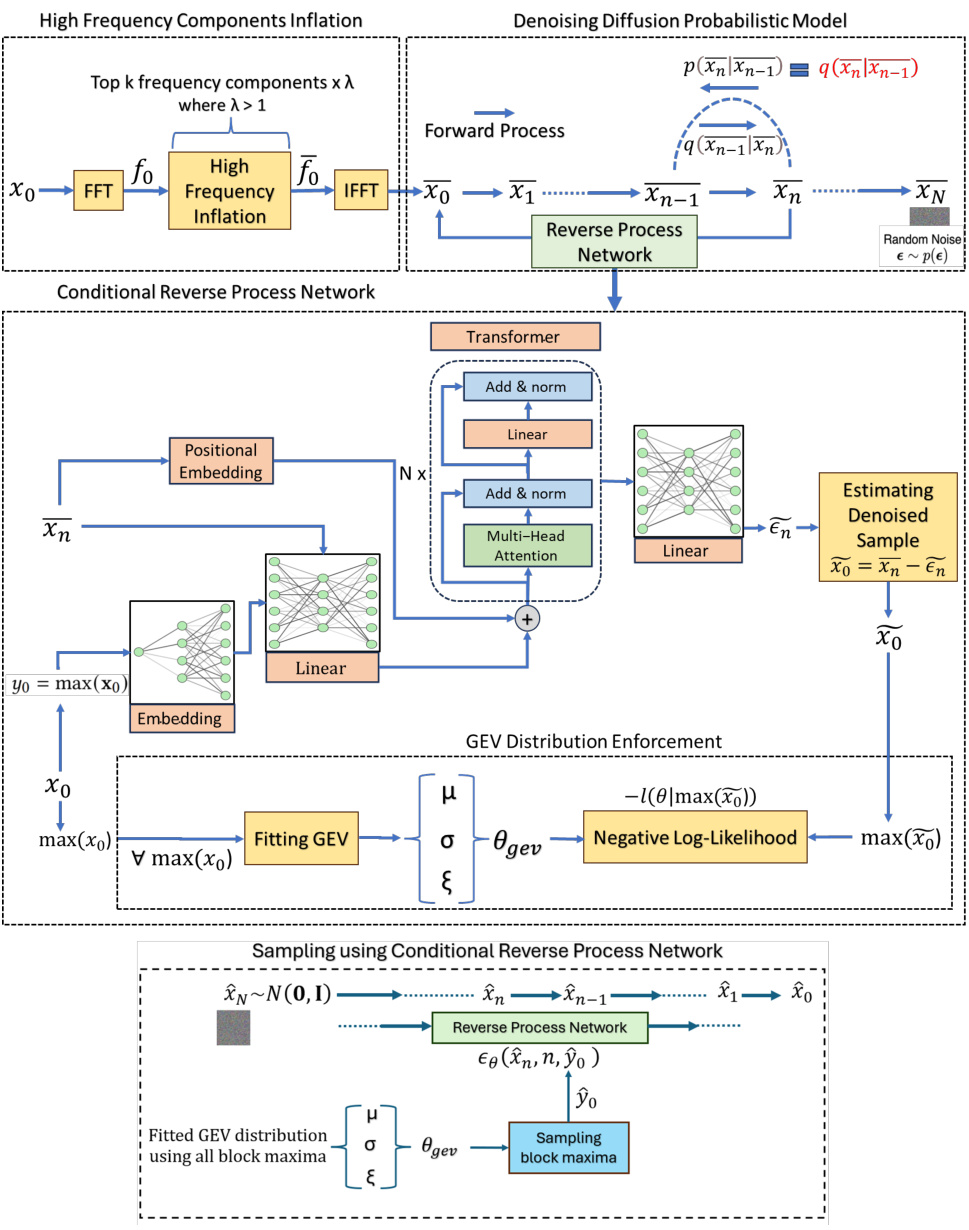
This figure presents a detailed illustration of the FIDE (Frequency-Inflated Conditional Diffusion Model) framework. The framework consists of several key stages, beginning with high-frequency component inflation in the frequency domain, followed by a denoising diffusion probabilistic model (DDPM) for the forward process, and a conditional reverse process network for generating samples conditioned on block maxima. The GEV (Generalized Extreme Value) distribution enforcement module ensures fidelity to both block maxima and overall data distribution. Finally, sampling is performed using the conditional reverse process network. The figure visually summarizes the entire process, from data preprocessing and transformation to the final generation of time series data with accurately represented extreme events.

This figure compares the distribution of all data points and the distribution of block maxima in a synthetic AR(1) dataset. The left panel shows the distribution of all values in the dataset, comparing the real data distribution to that generated by the Denoising Diffusion Probabilistic Model (DDPM). The right panel shows the same comparison, but focuses only on the block maxima values. The visualization clearly illustrates that DDPM struggles to accurately model the distribution of the block maxima, highlighting the challenge that FIDE aims to address.

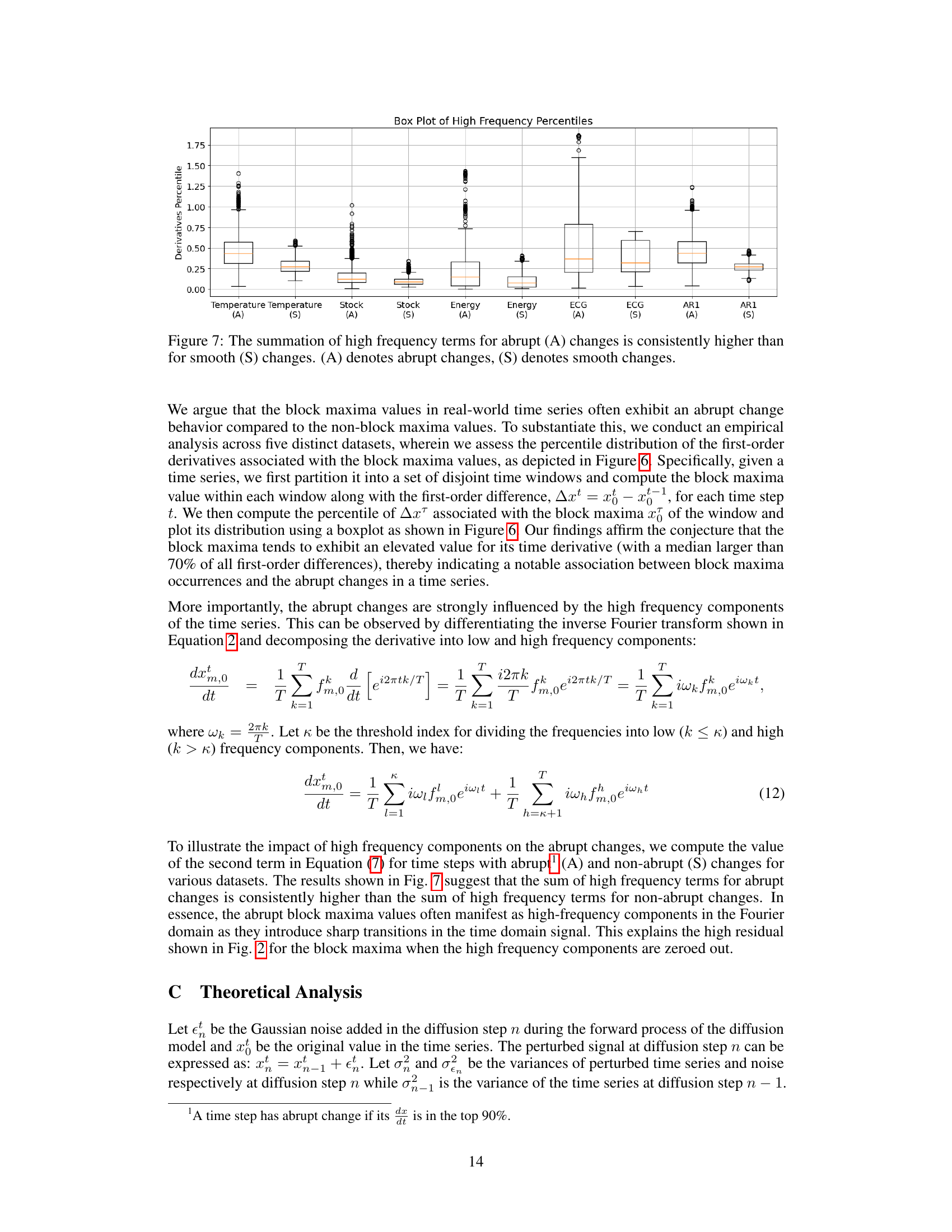
This box plot visualizes the distribution of first-order derivatives for block maxima across various datasets (Temperature, Stock, Energy, ECG, AR1). Each box represents a dataset, showing the median, interquartile range (IQR), and outliers. The figure illustrates that the derivatives associated with block maxima frequently show elevated percentile values, suggesting a correlation between abrupt changes and the occurrence of block maxima.

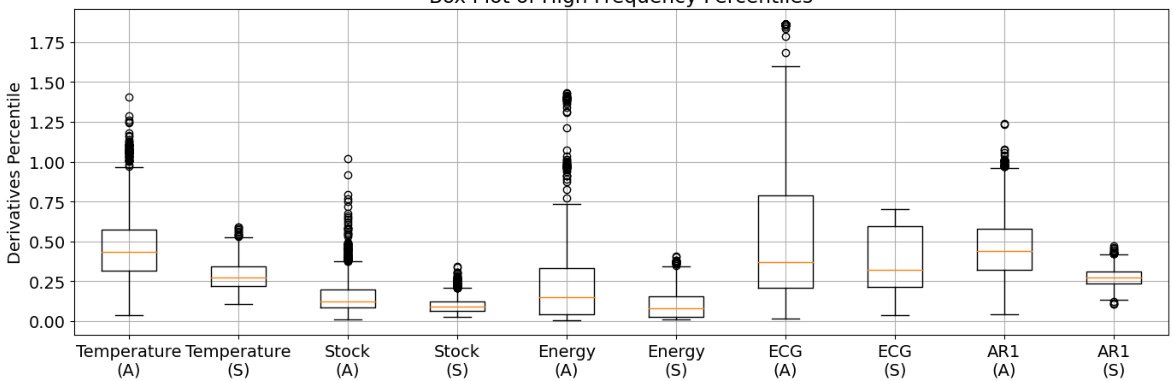
This figure is a box plot showing the percentile distribution of the summation of high-frequency terms in the Fourier transform of time series data. It compares the distribution for time points with abrupt changes in value (labeled ‘A’) against those with smooth changes (‘S’). The data is shown for several datasets, highlighting the higher frequency components and larger magnitude of change associated with abrupt shifts.

More on tables

This table compares the performance of the proposed FIDE model against several other generative models for time series data. It evaluates how well each model captures the distribution of block maxima values (extreme values) and also measures the predictive accuracy of each model using a separate time series forecasting model. The metrics used include the Jensen-Shannon (JS) divergence, Kullback-Leibler (KL) divergence, Continuous Ranked Probability Score (CRPS), and Predictive Score. The best and second-best results for each metric are highlighted.

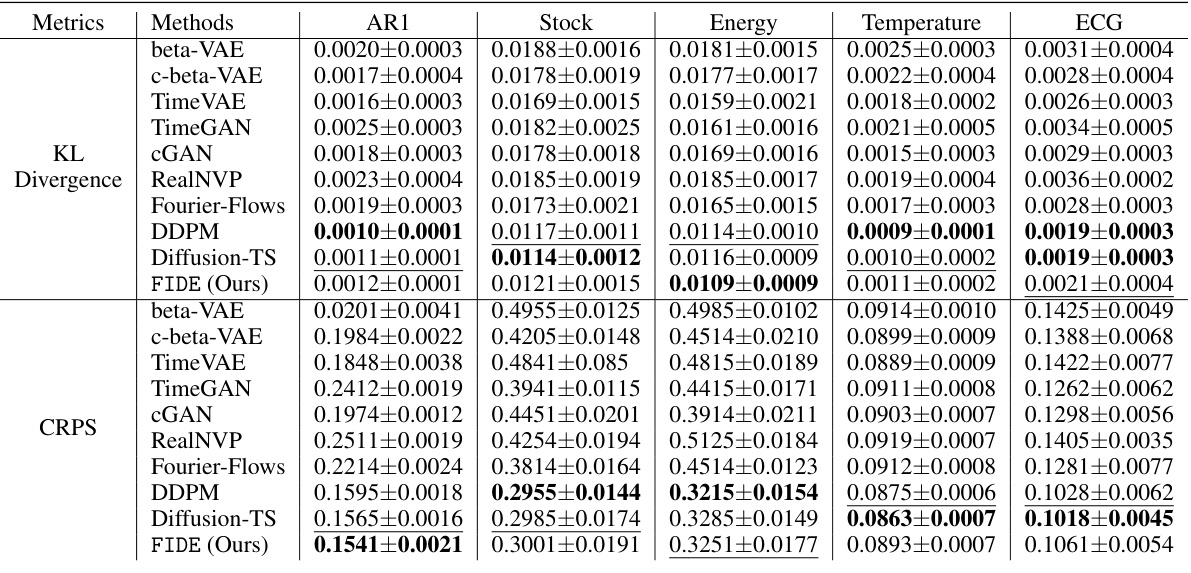
This table presents a comparison of different time series generation methods based on several metrics. These metrics evaluate how well each method captures the distribution of block maxima (extreme values) and how accurately it predicts future values in the time series. The methods compared include various GAN, VAE, Flow, and Diffusion-based models. The table shows the performance of each method on five different datasets: AR1 (synthetic), Stock (financial), Energy (appliance energy), Temperature (daily minimum), and ECG (medical). The best and second-best performing methods for each dataset and metric are highlighted.

This table presents the quantitative comparison of the proposed FIDE model against various baseline methods across multiple datasets (AR1, Stock, Energy, Temperature, ECG) and evaluation metrics. The metrics include Jensen-Shannon Divergence, KL Divergence, CRPS (Continuous Ranked Probability Score), and Predictive Score. The best and second-best results for each metric and dataset are highlighted in bold and underlined, respectively. The table offers a comprehensive overview of the FIDE model’s performance relative to other generative models in capturing block maxima distribution and predicting future time series values.

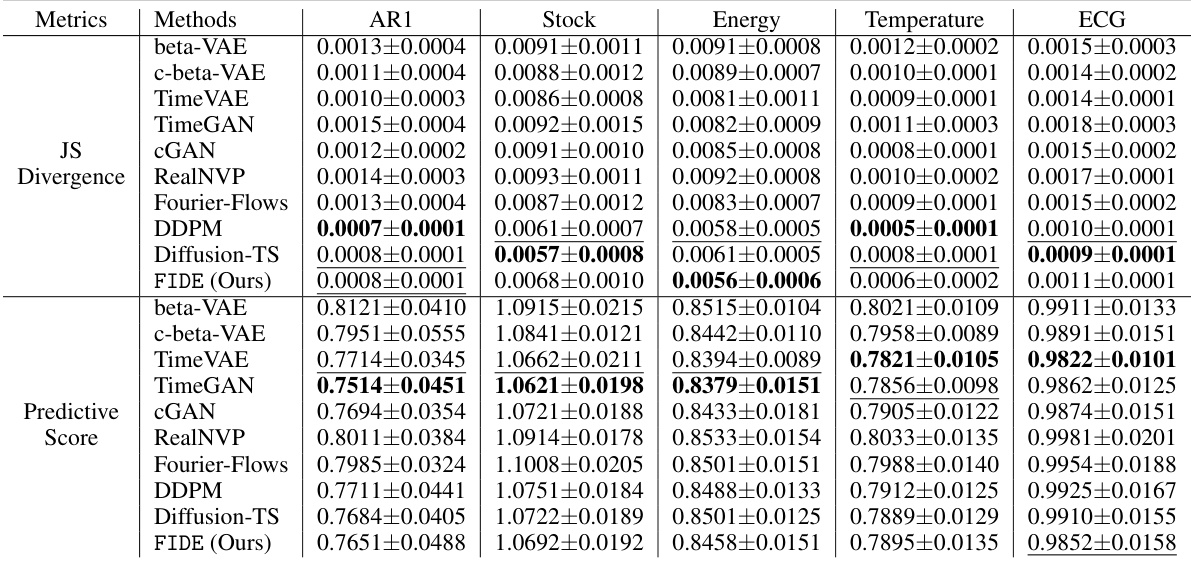
This table presents the quantitative comparison of the proposed FIDE model against several state-of-the-art baselines across five different datasets. The evaluation is performed using four metrics: Jensen-Shannon Divergence, KL Divergence, CRPS (Continuous Rank Probability Score), and Predictive Score. The metrics assess how well each model captures the block maxima distribution and its predictive performance. Bold and underlined values highlight the best and second-best performing models for each metric and dataset.

Full paper

#