TL;DR#
Many scientific fields rely on the Benjamini-Hochberg (BH) procedure to control the false discovery rate (FDR) in multiple hypothesis testing. This is critical in applications where false positives are costly. However, this paper investigates whether BH is robust against adversarial attacks, where an attacker may try to manipulate data or the testing process to produce undesired outcomes.
The researchers found that BH’s FDR control can be significantly compromised by relatively few test score perturbations. They introduced a class of easily implementable adversarial algorithms that can break BH’s FDR control. The analysis connects the BH procedure to a “balls into bins” process, facilitating a new information-theoretic approach for analyzing the adversary’s effect. The paper provides non-asymptotic guarantees on how much the FDR is affected by these adversarial attacks and shows through simulations that this impact can be substantial.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in statistics, machine learning, and related fields because it highlights a vulnerability in a widely-used statistical method (Benjamini-Hochberg procedure). This vulnerability is particularly relevant in safety-critical applications where false positives are costly. The findings necessitate a re-evaluation of the method’s reliability in adversarial environments, and provide researchers with new tools to assess and enhance the robustness of their statistical methods, including novel perturbation algorithms.
Visual Insights#
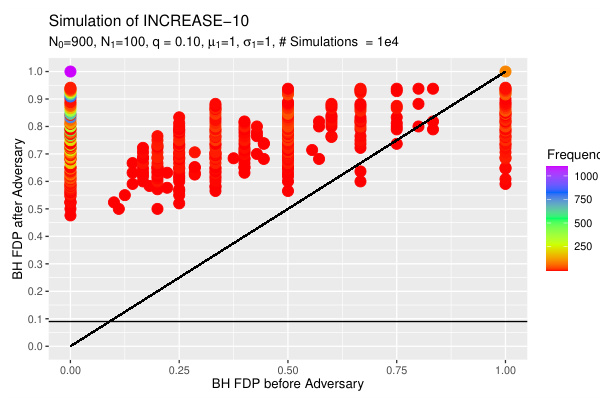
🔼 This figure shows the results of 104 simulations comparing the false discovery proportion (FDP) before and after applying the INCREASE-10 algorithm to a set of z-scores. The x-axis represents the FDP before the adversarial attack (using the Benjamini-Hochberg procedure), and the y-axis shows the FDP after the attack. Each point represents a single simulation. The parameters used are N=103 (total number of tests), No=900 (number of null hypotheses), and q=0.10 (FDR control level). The plot demonstrates that INCREASE-10 consistently increases the FDP.
read the caption
Figure 1: 104 simulations of FDP by BHq before and after INCREASE-10 is executed on the z-scores. N = 103, No = 900, and q = 0.10.

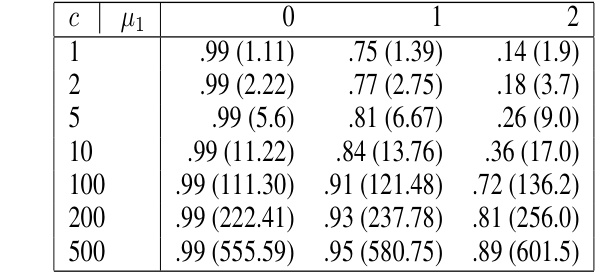
🔼 This table presents the results of a real-data experiment on credit card fraud detection using the Benjamini-Hochberg procedure. It shows the average false detection proportion (FDP) before and after applying the INCREASE-c algorithm with different values of c (corruption budget). The table also displays the average number of alleged frauds before and after the adversarial attack. The results illustrate how INCREASE-c can increase the FDR (false discovery rate) beyond the control level.
read the caption
Table 2: Credit Card Fraud Detection Experiment
In-depth insights#
BH’s Adversarial Weakness#
The Benjamini-Hochberg (BH) procedure, while robust in controlling the false discovery rate (FDR) under various distributional assumptions, exhibits significant vulnerabilities to adversarial attacks. The core weakness lies in its reliance on the ordering of p-values. A small number of strategically perturbed p-values can drastically inflate the FDR, effectively breaking BH’s control. This is especially true when the alternative distributions are not strongly separated from the null distribution. The authors demonstrate that this adversarial vulnerability isn’t just a theoretical concern; they present algorithms that empirically showcase this susceptibility with both synthetic and real-world data, highlighting the importance of considering adversarial robustness when relying on BH for critical safety and security applications. The research underscores the need for developing more robust multiple testing procedures capable of withstanding intentional data manipulation.
INCREASE-c Algorithm#
The INCREASE-c algorithm, designed for adversarial attacks against the Benjamini-Hochberg (BH) multiple testing procedure, strategically perturbs c null p-values to inflate the false discovery rate (FDR). Its core mechanism involves identifying a stopping time k, representing the BH procedure’s rejection count, and increasing it by at least c. The algorithm’s effectiveness hinges on the distribution of alternative p-values: when alternatives are highly sub-uniform (concentrated near 0), the impact is minimal because BH already rejects many of them. However, when alternatives are less sub-uniform, or close to uniform, the INCREASE-c algorithm can significantly break BH’s FDR control, even with few perturbations. The algorithm’s simplicity and effectiveness, particularly in situations where alternatives are barely dominated by the null distribution, highlights a vulnerability in the BH procedure’s robustness against adversarial manipulations. The algorithm provides a practical demonstration of how easily a seemingly robust statistical procedure can be compromised when subjected to cleverly designed attacks.
FDR Control Limits#
The concept of ‘FDR Control Limits’ in multiple hypothesis testing revolves around setting boundaries for the acceptable rate of false discoveries. The False Discovery Rate (FDR) is a crucial metric, representing the expected proportion of false positives among all rejected null hypotheses. Establishing these limits is paramount, as it directly impacts the reliability and validity of the results. Setting limits too leniently can inflate the FDR, leading to an unacceptably high number of false positives. Conversely, limits that are too stringent might lead to an excessive number of false negatives, thus potentially missing true discoveries. Therefore, the determination of optimal FDR control limits involves a careful balance between these two extremes, often guided by the specific context and the associated risks and costs associated with making incorrect conclusions. The choice of these limits often depends on predefined thresholds, statistical power considerations, and the overall goal of the research. A deeper analysis of the procedure employed and its underlying assumptions (statistical dependence, distributions) is necessary to gauge the effectiveness of the FDR control and determine the reliability of the conclusions drawn.
Synthetic Data Tests#
Synthetic data tests are crucial for evaluating the robustness and generalizability of machine learning models, especially in scenarios with limited real-world data. These tests allow researchers to systematically assess model performance under controlled conditions, manipulating various aspects of the data to understand their impact on the model’s predictions. A key advantage is the ability to generate data sets with specific characteristics, including carefully controlled levels of noise, outliers, and adversarial examples, which enables targeted investigations of model vulnerabilities. Well-designed synthetic tests can highlight weaknesses that might be missed or obscured in real-world data analysis due to confounding variables or insufficient data volume. However, a critical consideration is the representativeness of the synthetic data to the real-world phenomenon. If the synthetic data generation process doesn’t accurately capture the essential characteristics of real data, the resulting analysis may lead to misleading conclusions. Therefore, rigorous validation and comparison of model performance across synthetic and real-world datasets are essential to ensure that findings obtained using synthetic data tests are meaningful and applicable in practice.
Future Research#
Future research directions stemming from this work could explore extensions to more complex adversarial models. The current analysis focuses on an omniscient adversary; investigating the robustness of the Benjamini-Hochberg procedure against more realistic adversaries with limited knowledge or computational power would be valuable. Additionally, the study could be expanded to other multiple testing procedures, such as those based on different error rates or handling different dependency structures, to determine the extent to which adversarial vulnerabilities are common to various approaches. Further research could also delve into mitigation strategies, developing methods to enhance the adversarial robustness of multiple testing procedures or designing robust alternatives. A promising direction is to analyze how various data preprocessing or regularization techniques affect adversarial resilience. Finally, empirical studies on diverse real-world datasets across multiple domains are critical for validating theoretical findings and guiding the development of practically effective methods for safeguarding hypothesis testing against adversarial attacks.
More visual insights#
More on figures
🔼 This figure shows the results of 104 simulations comparing the false discovery proportion (FDP) before and after applying the INCREASE-10 algorithm. The x-axis represents the FDP before the algorithm, and the y-axis represents the FDP after. Each point represents a single simulation. The parameters used are N=1000 tests, 900 null hypotheses, a control level q=0.10. The plot demonstrates that INCREASE-10 consistently increases the FDP, showing its effectiveness in compromising the BH procedure’s FDR control.
read the caption
Figure 1: 104 simulations of FDP by BHq before and after INCREASE-10 is executed on the z-scores. N = 103, No = 900, and q = 0.10.
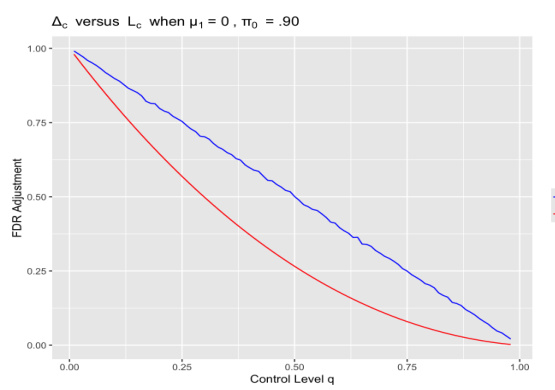
🔼 This figure compares the actual FDR increase (∆₁) caused by the INCREASE-1 algorithm with the theoretical lower bound (L₁) derived in Theorem 4.5. The comparison is shown across various control levels (q) when the mean of alternative distributions (µ₁) is 0 and the total number of tests (N) is 1000. This illustrates how well the theoretical bound approximates the actual adversarial impact of the algorithm under specific conditions.
read the caption
Figure 2: Comparing the FDR increase ∆₁ of INCREASE-1 with the lower bound L₁ of Theorem 4.5 as functions of q when µ₁ = 0, N = 1000

🔼 This figure compares the actual FDR increase (Δ₁) achieved by the INCREASE-1 algorithm against the theoretical lower bound (L₁) derived in Theorem 4.5, as a function of the control level (q). The parameters used are μ₁ = 0.25, N = 1000, and c = 1. It shows how well the theoretical bound approximates the actual adversarial effect for different control levels. The discrepancy provides insights into the degree of adversarial robustness under different control level settings.
read the caption
Figure 3: Comparing the FDR increase Δ₁ of INCREASE-1 with the lower bound L₁ of Theorem 4.5 as functions of q when μ₁ = .25, N = 1000

🔼 This figure shows the results of 103 simulations comparing the false discovery proportion (FDP) of the Benjamini-Hochberg (BHq) procedure before and after applying the INCREASE-5 algorithm. The conformal p-values used were derived from a one-class SVM classifier on a test set containing outliers. The parameter ‘a’ controls the level of separation between the inliers and outliers, with a=1.5 indicating a moderate level of separation. The x-axis represents FDP before applying INCREASE-5, and the y-axis represents FDP after applying INCREASE-5. Each point represents a single simulation, and the color intensity reflects the frequency of observations in that region. The black line represents the theoretical FDR control level (0.1). The plot shows that INCREASE-5 significantly increases the FDP in many simulations, demonstrating its effectiveness in breaking the FDR control of BHq even with relatively simple adversarial perturbations.
read the caption
Figure 4: 103 simulations of FDP by BHq with and without application of INCREASE-5 on marginal conformal p-values [5] derived from an SVM one-class classifier on a test set with outliers drawn with a = 1.5.
Full paper#



















