TL;DR#
Conformal Prediction (CP) offers statistically valid prediction sets but struggles when test data is altered adversarially. Existing methods using randomized smoothing have limitations, only supporting l2-bounded perturbations and classification tasks. They also produce overly conservative predictions.
This research introduces Verifiably Robust Conformal Prediction (VRCP), a novel framework addressing these limitations. VRCP leverages neural network verification to create robust prediction sets, handling various norms and both classification and regression tasks. Its evaluations show VRCP achieves higher nominal coverage and more precise prediction sets than the current state-of-the-art methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it introduces a novel framework, VRCP, that enhances the robustness of conformal prediction against adversarial attacks. This is highly relevant given the increasing importance of reliable uncertainty quantification in machine learning, particularly in safety-critical applications. VRCP’s ability to handle various norms and both classification and regression tasks significantly expands its applicability and potential impact.
Visual Insights#
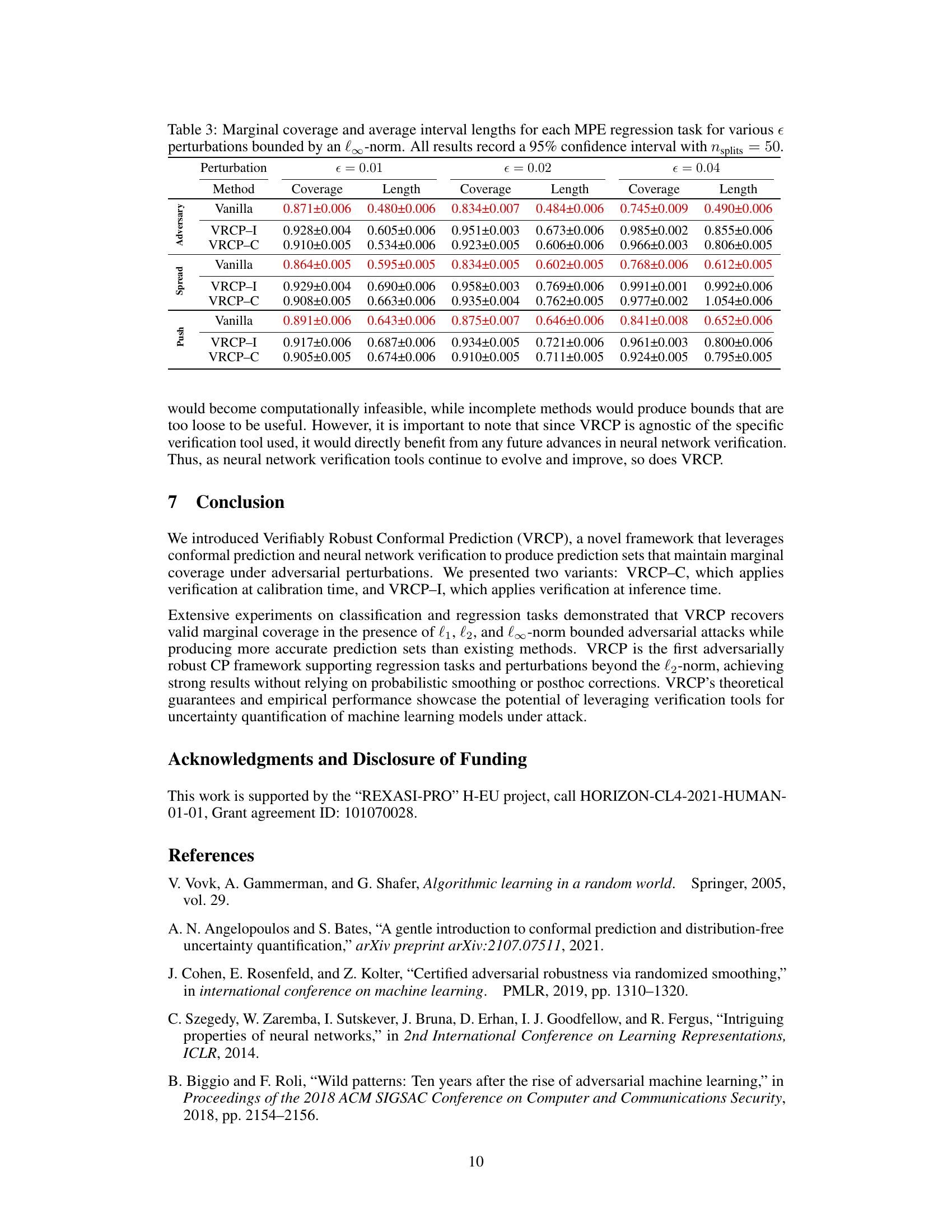
🔼 The figure shows the distribution of prediction set sizes for different conformal prediction methods on the CIFAR10 dataset under adversarial attacks. Vanilla CP violates the coverage guarantee, while VRCP-I and VRCP-C maintain it and have similar set size distributions to vanilla CP. The state-of-the-art methods (RSCP+ and RSCP+ with post-training transformation (PTT)) fail to achieve the same level of performance, producing much larger prediction sets.
read the caption
Figure 1: Distribution of prediction set sizes for vanilla conformal prediction (vanilla CP) which violates Eq. (2), as well as for our proposed robust algorithms (VRCP–I and VRCP–C) along with the SotA (RSCP+ and RSCP+ (PTT), see Section 3) on the CIFAR10 dataset. As we observe, VRCP-I and VRCP-C closely resemble the spread of vanilla CP prediction set sizes, whilst the SotA falls short of achieving this. Here we use an adversarial perturbation of radius € = 0.02, error rate a = 0.1, number of splits nsplits = 50 and smoothing parameter (used in RSCP+ and RSCP+ (PTT)) σ = 2€.
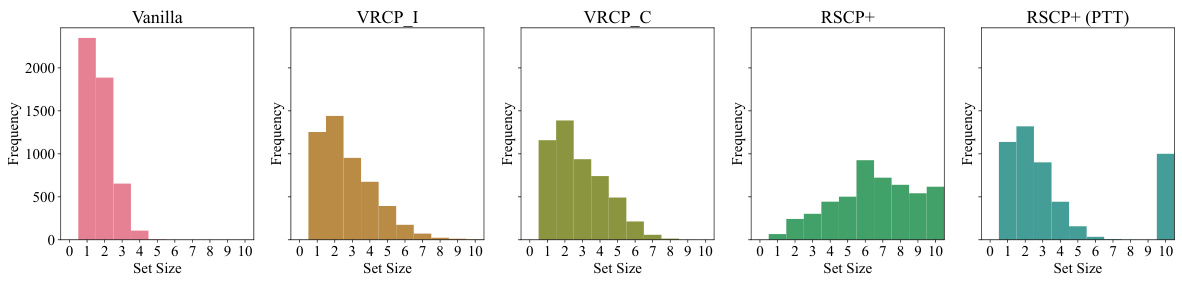
🔼 This table presents the results of the experiments comparing different methods for conformal prediction under adversarial attacks. It shows the marginal coverage and average set sizes for vanilla conformal prediction, RSCP+, RSCP+ with post-training transformation (PTT), VRCP-I, and VRCP-C on three image classification datasets: CIFAR10, CIFAR100, and TinyImageNet. The results are reported with 95% confidence intervals based on 50 splits of the data. The parameter settings (α, σ, nmc, ε) are also specified.
read the caption
Table 1: Marginal Coverage and Average Set Sizes for different methods on CIFAR10, CIFAR100 and TinyImageNet. All results record a 95% confidence interval with nsplits = 50, α = 0.1, σ = 2ε, nmc = 1024, ε = 0.03 for CIFAR10 and ε = 0.02 otherwise.
In-depth insights#
Robust Conformal Prediction#
Robust Conformal Prediction (RCP) enhances the traditional Conformal Prediction (CP) framework by addressing its vulnerability to adversarial attacks and distributional shifts. Standard CP guarantees coverage of the true output with a specified probability, assuming exchangeability between training and test data. However, this assumption often fails under real-world conditions with noisy or manipulated inputs. RCP methods modify the CP algorithm to maintain valid coverage even when facing such challenges. This often involves techniques that either inflate prediction sets to account for uncertainty introduced by perturbations, or employ robust statistical methods. Key improvements over standard CP include better coverage guarantees in adversarial settings and more efficient prediction regions. However, the increased robustness often comes at the cost of increased computational complexity, especially when using advanced verification techniques for neural network predictions. A crucial aspect of RCP is the choice of norm used to define the size of adversarial perturbations. Different norms lead to varied computational challenges and robustness guarantees.
NN Verification Methods#
Neural network verification (NNV) methods are crucial for ensuring the robustness and reliability of deep learning models, especially in safety-critical applications. Complete methods guarantee the verification of properties across all possible inputs within a given perturbation bound, but are computationally expensive. Incomplete methods, conversely, provide sound but not necessarily complete verification, trading off precision for speed. Different approaches exist such as those leveraging interval bound propagation, abstract interpretation, or combinations of these techniques. The choice of method often involves a trade-off between accuracy and computational cost. Future research should focus on developing more efficient and scalable complete methods and exploring the synergies between different approaches to achieve both strong guarantees and fast execution times. This is particularly important in the context of applications like autonomous driving and medical diagnosis where reliability is paramount.
Adversarial Robustness#
Adversarial robustness is a crucial concept in machine learning, particularly concerning the vulnerability of models to adversarial attacks. These attacks involve subtle, often imperceptible, modifications to input data that can cause a model to misclassify or produce erroneous outputs. The paper explores methods to enhance adversarial robustness in the context of conformal prediction (CP), a technique for providing valid prediction sets. The core challenge lies in ensuring that the CP guarantees remain valid even when the data is subjected to adversarial perturbations. The proposed Verifiably Robust Conformal Prediction (VRCP) framework uses neural network verification to create robust prediction sets that provide coverage guarantees under adversarial attacks, achieving above-nominal coverage and more informative prediction regions than existing methods. A key aspect of this approach is its ability to support different norms, addressing a significant limitation of previous techniques that primarily focus on l2-norm bounded perturbations. The work signifies a significant step forward in creating dependable and trustworthy machine learning models in the face of malicious or noisy inputs.
Beyond L2 Norm#
The section ‘Beyond L2 Norm’ would delve into the paper’s extension of adversarial robustness beyond the commonly used L2 norm. This is crucial because real-world attacks aren’t confined to L2-bounded perturbations. The discussion would likely showcase the framework’s ability to handle L1 and L∞ norm-bounded attacks, highlighting its enhanced applicability and practical relevance. The paper would likely present empirical results demonstrating the effectiveness of the proposed method against these different attack types, comparing its performance with existing approaches. A key aspect would be showing that the method maintains statistically valid prediction sets even under these broader attack scenarios, thereby emphasizing its superior robustness and generality compared to methods limited to the L2 norm.
Empirical Validations#
An empirical validation section in a research paper would typically present results from experiments designed to test the paper’s claims. It would likely involve a description of the experimental setup, datasets used, metrics employed, and a detailed analysis of the findings. A strong validation section would not only demonstrate that the proposed method works as expected but also compare it against existing baselines, highlighting improvements and addressing potential limitations. The presentation of results should be clear, concise, and visually appealing. Appropriate statistical measures should be included to convey the significance of the findings, such as confidence intervals or p-values. A thorough discussion of the results would be essential, interpreting the implications of the experiments and addressing potential biases. It is crucial to ensure that the validation strategy is rigorous and comprehensive, addressing potential sources of error and providing a nuanced interpretation of the results. The ultimate aim of the section is to build confidence in the robustness and generalizability of the claims made in the paper.
More visual insights#
More on figures

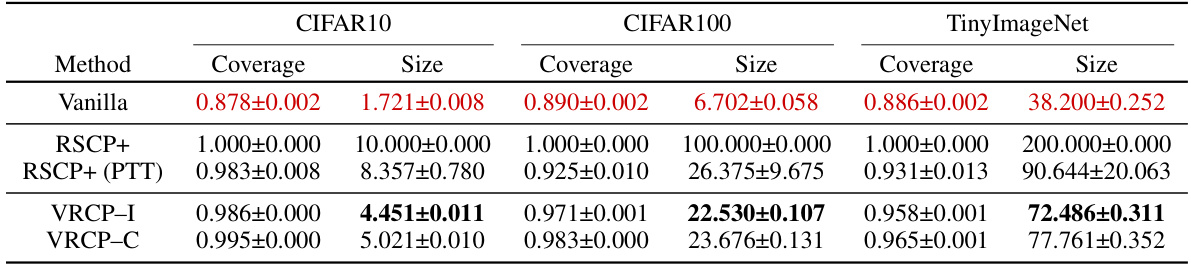
🔼 This figure shows the impact of increasing the number of Monte Carlo samples (nmc) and the impact of increasing epsilon (e) on the marginal coverage and average set sizes of various methods, including VRCP-I, VRCP-C, RSCP+, and RSCP+ (PTT). The left panel displays results varying nmc, while keeping epsilon constant; the right panel shows results by varying epsilon while keeping nmc constant. The shaded regions represent the 95% confidence intervals. The figure demonstrates VRCP’s robustness in maintaining nominal coverage across varying hyperparameter values while producing significantly smaller prediction regions than the comparison methods.
read the caption
Figure 2: Marginal Coverage and Average Set Sizes on CIFAR100 with 95% confidence intervals.
🔼 This figure shows the impact of increasing the size of adversarial perturbations (epsilon) on both marginal coverage and average prediction set size for different methods on the CIFAR100 dataset. It compares the performance of VRCP-I, VRCP-C, RSCP+, and RSCP+ (PTT). The x-axis represents the magnitude of adversarial perturbations (epsilon), while the y-axis on the left shows the marginal coverage and the y-axis on the right shows the average prediction set size. The shaded areas represent 95% confidence intervals. The figure demonstrates that VRCP methods maintain high coverage while producing relatively smaller prediction sets compared to the other methods.
read the caption
Figure 2: Marginal Coverage and Average Set Sizes on CIFAR100 with 95% confidence intervals.
More on tables
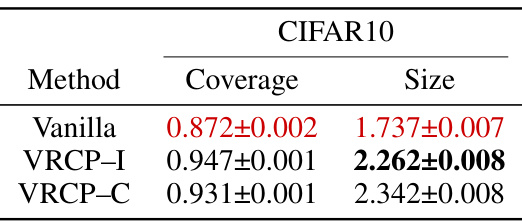
🔼 This table presents the results of evaluating different conformal prediction methods on the CIFAR10 dataset using the l∞-norm for adversarial attacks. It shows the marginal coverage and average set sizes for vanilla conformal prediction, VRCP-I, and VRCP-C, demonstrating that VRCP methods achieve higher coverage while maintaining relatively small set sizes compared to vanilla CP, even under l∞-norm attacks.
read the caption
Table 2: Marginal Coverage and Average Set Sizes for e perturbations with respect to the l∞-norm on the CIFAR10 dataset. All results record a 95% confidence interval with splits = 50, α = 0.1 and ε = 0.001.

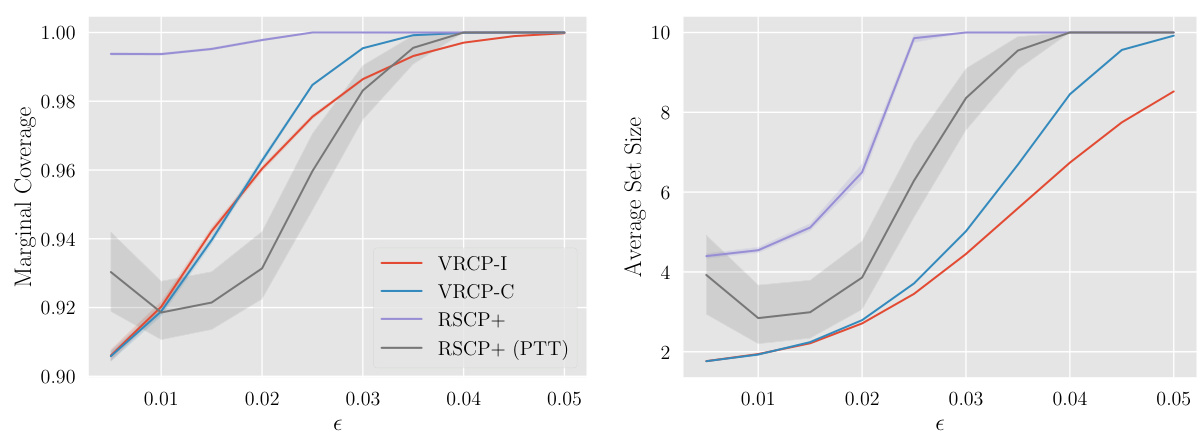
🔼 This table presents the results of evaluating the performance of vanilla CP, VRCP-I, and VRCP-C on three different multi-agent particle environment (MPE) regression tasks. The performance is evaluated under different levels of adversarial perturbations (epsilon values) bounded by the l∞-norm. The table shows the marginal coverage and average interval lengths for each method and perturbation level, providing a quantitative comparison of their robustness and efficiency in handling adversarial attacks in regression settings.
read the caption
Table 3: Marginal coverage and average interval lengths for each MPE regression task for various e perturbations bounded by an l∞-norm. All results record a 95% confidence interval with nsplits = 50.

🔼 This table presents the marginal coverage and average set sizes for different conformal prediction methods on three image classification datasets: CIFAR10, CIFAR100, and TinyImageNet. The results show the performance of vanilla conformal prediction, randomly smoothed conformal prediction (RSCP+) with and without post-training transformation (PTT), and the proposed Verifiably Robust Conformal Prediction (VRCP) methods (VRCP-I and VRCP-C). The table indicates the achieved coverage and average prediction set size for each method, providing a comparison of their effectiveness in maintaining coverage under adversarial attacks.
read the caption
Table 1: Marginal Coverage and Average Set Sizes for different methods on CIFAR10, CIFAR100 and TinyImageNet. All results record a 95% confidence interval with nsplits = 50, α = 0.1, σ = 2ε, nmc = 1024, ε = 0.03 for CIFAR10 and ε = 0.02 otherwise.

🔼 This table presents the results of the regression experiments on the three MPE tasks (Adversary, Spread, and Push) with different levels of \ell_\infty-norm bounded adversarial perturbations. It shows the marginal coverage and average interval lengths for the vanilla CP method and the proposed VRCP-I and VRCP-C methods. The results are averaged over 50 splits and reported with 95% confidence intervals.
read the caption
Table 3: Marginal coverage and average interval lengths for each MPE regression task for various \epsilon perturbations bounded by an \ell_\infty-norm. All results record a 95\% confidence interval with \textit{nsplits} = 50.
Full paper#