TL;DR#
Offline reinforcement learning (RL) faces challenges due to the discrepancy between the state-action distribution of available data and the target policy’s distribution. Existing methods often rely on strong assumptions about data coverage, which limits their real-world applicability. This constraint is particularly problematic in domains like autonomous driving and healthcare where comprehensive data collection is expensive or infeasible.
This paper introduces a novel approach called worst-case offline RL. This method addresses the issue by using a new performance metric that considers the worst-case policy value across all possible environments consistent with the observed data. The authors develop a model-free algorithm, Worst-case Minimax RL (WMRL), based on this framework and prove it achieves a sample complexity bound of O(ε⁻²). This bound holds even without any assumptions about the data support or coverage, signifying a significant improvement over existing offline RL methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a novel solution to a critical problem in offline reinforcement learning (RL): the distributional discrepancy between training data and target policies. This limitation severely restricts the applicability of offline RL in real-world scenarios. The proposed method provides a strong theoretical foundation and opens avenues for robust offline RL algorithms with guaranteed performance, paving the way for wider applications.
Visual Insights#
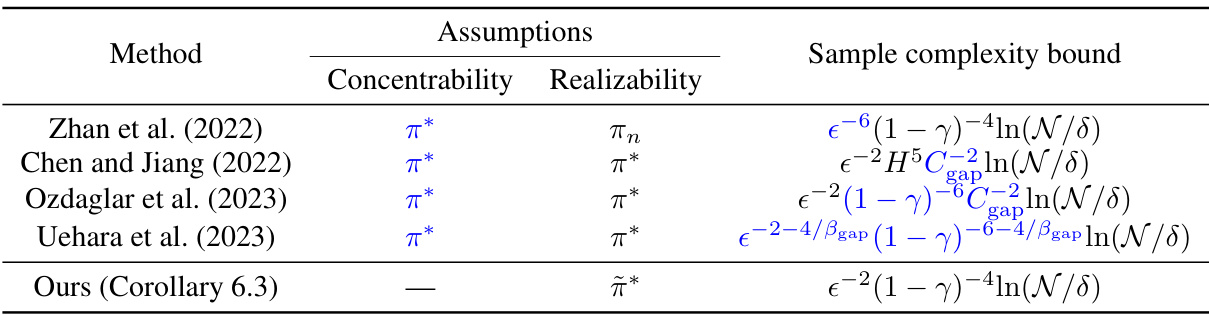
🔼 This table compares the sample complexity bounds of different offline reinforcement learning methods. It highlights the assumptions made by each method (concentrability and realizability) and shows how these assumptions affect the resulting sample complexity bound. The table emphasizes the improvement achieved by the proposed method in terms of both weaker assumptions and a tighter bound.
read the caption
Table 1: Assumptions and sample complexity bounds of related work. π* and π* denote optimal policies in the conventional and worst-case offline RL, respectively. πη denotes a sequence of policies indexed with the sample size n. The realizability of π means that π-associated model-free parameters (e.g., value functions, visitation weight functions and the policy itself) are realizable. ε > 0 is the policy suboptimality given in Problem 4.1 (or equivalently in Problem 3.1, see Corollary 4.2 for the equivalence). 0 < δ < 1 denotes the confidence parameter. H denotes the time horizon and roughly comparable to (1 – γ)−¹. Cgap and βgap denote the minimum and the lower-tail exponent of the action value gaps, respectively. N denotes the cardinality of the function classes. The improvements made by our result are emphasized. See Appendix A for more details.
Full paper#



















