TL;DR#
Molecular representation learning (MRL) is crucial for drug discovery and materials science. Traditional methods struggle with large and complex molecules. Recent advances in pretraining models for other domains (NLP, CV) have shown impressive results with scaling up model and dataset size. However, research into scaling laws in MRL is limited.
Uni-Mol2 addresses this gap by systematically investigating the scaling laws in MRL. The model leverages a two-track transformer architecture to integrate atomic, graph, and geometric features. The study uses a massive dataset (800 million conformations) and scales Uni-Mol2 to 1.1 billion parameters, surpassing existing methods. Results show consistent performance gains across various downstream tasks as the model size grows, highlighting the effectiveness of scaling in MRL.
Key Takeaways#
Why does it matter?#
This paper is crucial because it demonstrates the scaling laws in molecular pretraining, a relatively unexplored area. It introduces Uni-Mol2, a large-scale model, paving the way for future advancements in molecular representation learning and encouraging further research into scaling behaviors. This work is also significant for its extensive experiments and analysis of the impact of model and data size on performance across multiple datasets.
Visual Insights#
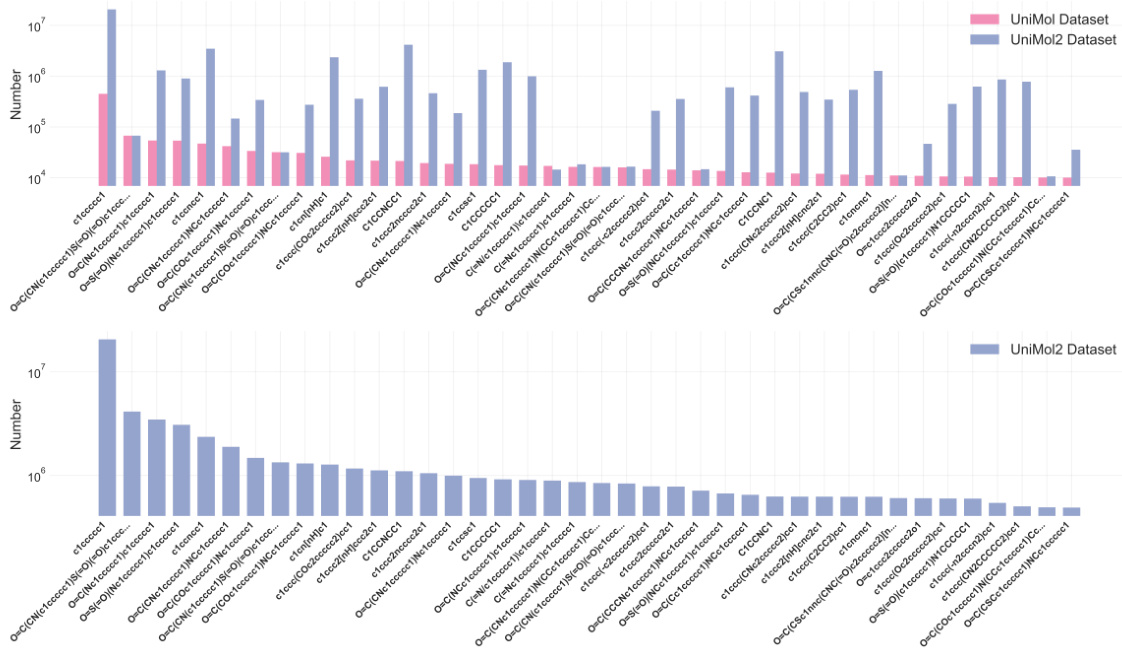
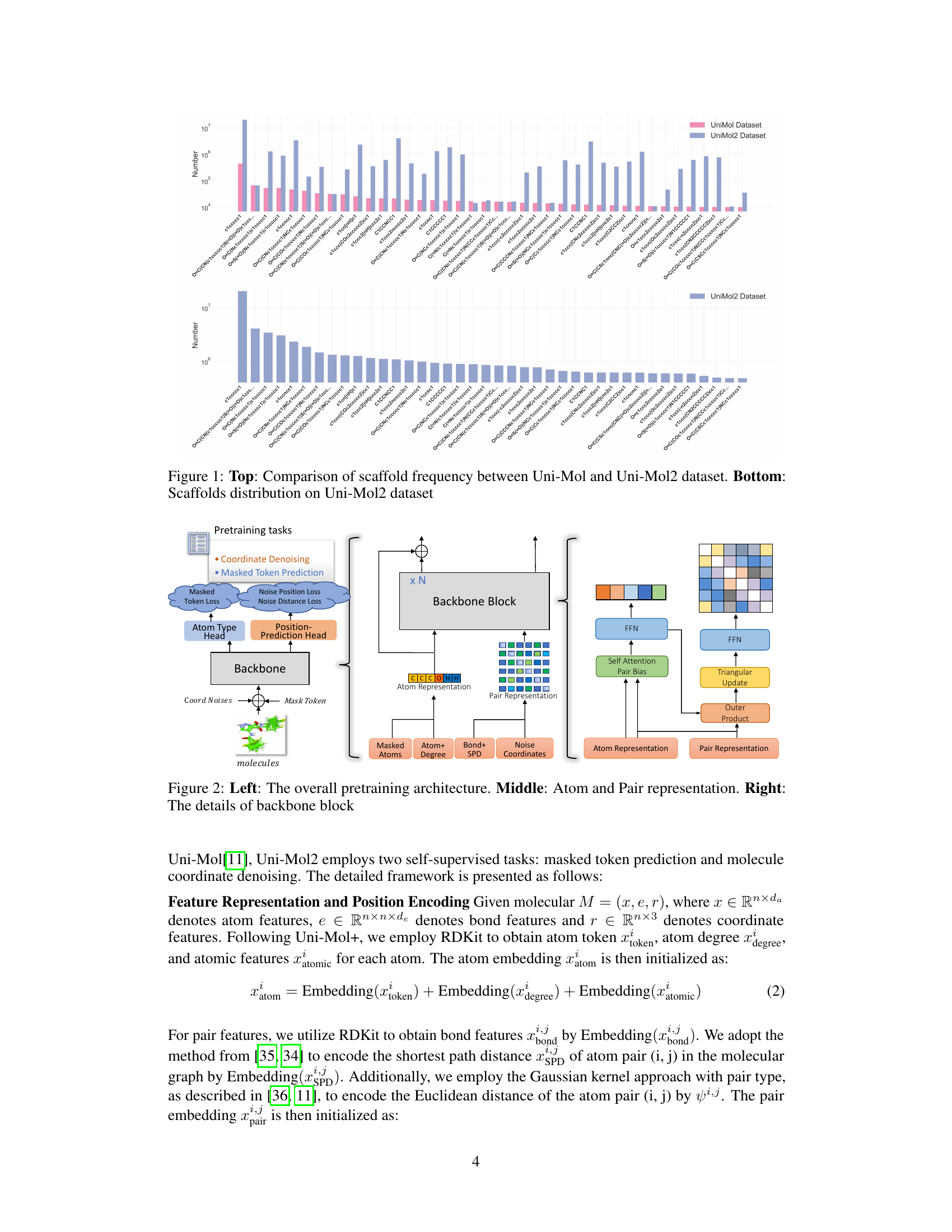
🔼 This figure compares the frequency distributions of the top 40 Murcko scaffolds in the Uni-Mol and Uni-Mol2 datasets. The top panel shows a bar chart comparing the counts of each scaffold in both datasets. The bottom panel presents a detailed bar chart illustrating the frequency distribution of scaffolds within the Uni-Mol2 dataset alone.
read the caption
Figure 1: Top: Comparison of scaffold frequency between Uni-Mol and Uni-Mol2 dataset. Bottom: Scaffolds distribution on Uni-Mol2 dataset

🔼 This table shows the different scales of the Uni-Mol and Uni-Mol2 datasets, including the number of SMILES, scaffolds, and data sources used in each dataset. Uni-Mol2 is significantly larger than Uni-Mol, which is important for the pretraining model.
read the caption
Table 1: The different scale of Uni-Mol dataset and Uni-Mol2 dataset
In-depth insights#
Mol Pretraining Scale#
The concept of “Mol Pretraining Scale” explores the scaling laws in molecular pretraining models. Larger models, trained on more extensive datasets, generally exhibit improved performance on downstream tasks. This research investigates the relationship between model size, dataset size, computational resources and validation loss, revealing power-law correlations. The study highlights the effectiveness of scaling molecular pretraining models, demonstrating consistent improvements as model size increases. The results emphasize the potential for significant advancements in molecular representation learning through scaling, paving the way for larger, more capable models in drug discovery and materials science. Uni-Mol2 serves as a prime example, achieving state-of-the-art results through its billion-parameter scale.
Uni-Mol2 Model#
The Uni-Mol2 model represents a significant advancement in molecular pretraining. Its novel two-track transformer architecture effectively integrates atomic, graph, and geometric features, leading to a more comprehensive molecular representation. This innovative approach, combined with a massive dataset of 800 million conformations, allows Uni-Mol2 to achieve state-of-the-art performance on downstream tasks like QM9 and COMPAS-1D. The research also demonstrates a clear scaling law, showing consistent performance improvements with increased model size and data, highlighting the potential for even larger and more powerful molecular models in the future. Uni-Mol2’s success underscores the value of scaling laws in molecular representation learning and opens exciting possibilities for future innovations in drug discovery and materials science.
Scaling Law Analysis#
The scaling law analysis section of this research paper is crucial for understanding the model’s performance improvements. It investigates the relationship between model performance (validation loss) and key factors: model size, dataset size, and computational resources. The researchers identify power-law correlations, demonstrating how increasing these factors leads to reduced validation loss. This analysis is essential for guiding future model development, as it provides a quantitative understanding of the returns on investment in scaling. A key finding is the demonstration of a scaling law in molecular pretraining models, something previously unexplored. This suggests that larger models trained on larger datasets and with greater computational resources will yield more significant improvements. The study’s power-law equations allow for prediction of performance based on resource allocation. The identification of this scaling law significantly advances the field, providing valuable insights for researchers looking to improve molecular representation learning.
Downstream Tasks#
The evaluation of downstream tasks is crucial for assessing the effectiveness of a molecular pretraining model. The paper meticulously investigates the performance of Uni-Mol2 on various downstream tasks, including QM9 and COMPAS-1D datasets. The results demonstrate a consistent improvement in performance as model size increases, showcasing the benefits of scaling up the model. This is particularly evident in the QM9 dataset where an average 27% improvement is observed with the largest model. However, it’s important to note that while the Uni-Mol2 model exhibits significant improvement over existing methods, certain tasks show saturation, indicating that model scaling may not always lead to linearly increasing performance. The detailed analysis of these results provides valuable insights into the relationship between model scale and task performance, offering guidance for future research in this area. Further exploration of the model’s capabilities on diverse and more challenging datasets is needed to fully understand its potential and limitations.
Future Directions#
Future research should explore extending Uni-Mol2’s capabilities beyond property prediction to encompass generative tasks, such as molecule design. Investigating whether the scaling benefits observed hold across a wider range of tasks and datasets is also crucial. Exploring alternative architectures, such as decode-only models, could enhance efficiency and scalability. Finally, a thorough investigation into optimizing hyperparameters like batch size and learning rate for various model scales is needed to maximize performance and resource utilization. These directions will refine Uni-Mol2 and broaden its applicability in various scientific domains.
More visual insights#
More on figures
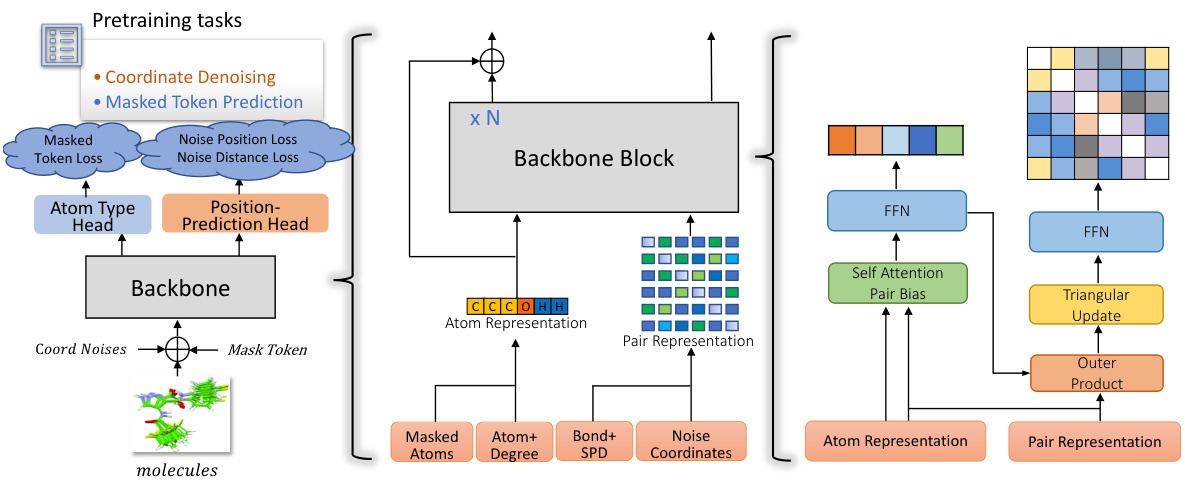
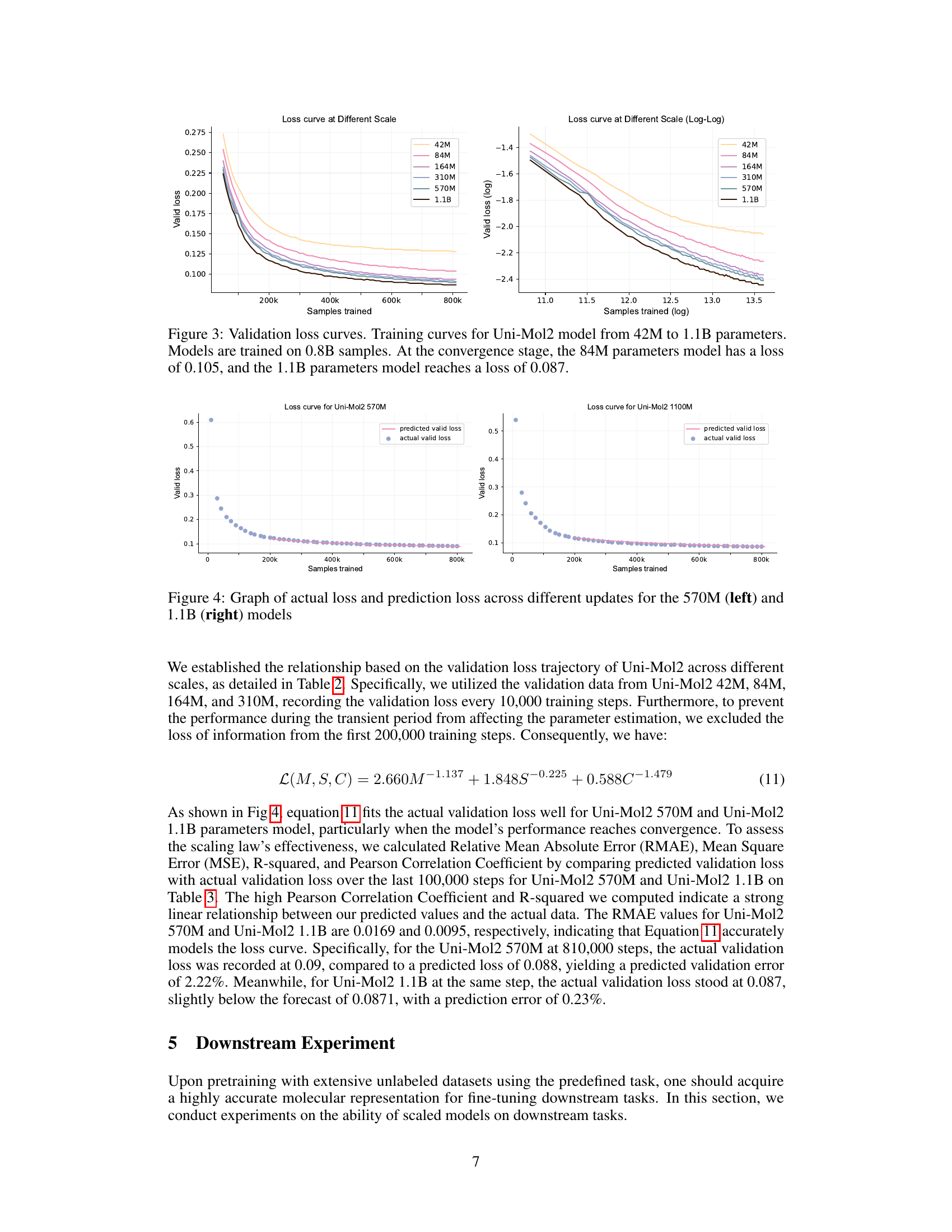
🔼 This figure illustrates the Uni-Mol2 model architecture. The left panel shows the overall architecture, including the two-track transformer that processes atom and pair features concurrently. The middle panel highlights how atom and pair representations are generated. The right panel provides details of the backbone block, outlining the specific components and processing steps for atom and pair features within each block.
read the caption
Figure 2: Left: The overall pretraining architecture. Middle: Atom and Pair representation. Right: The details of backbone block
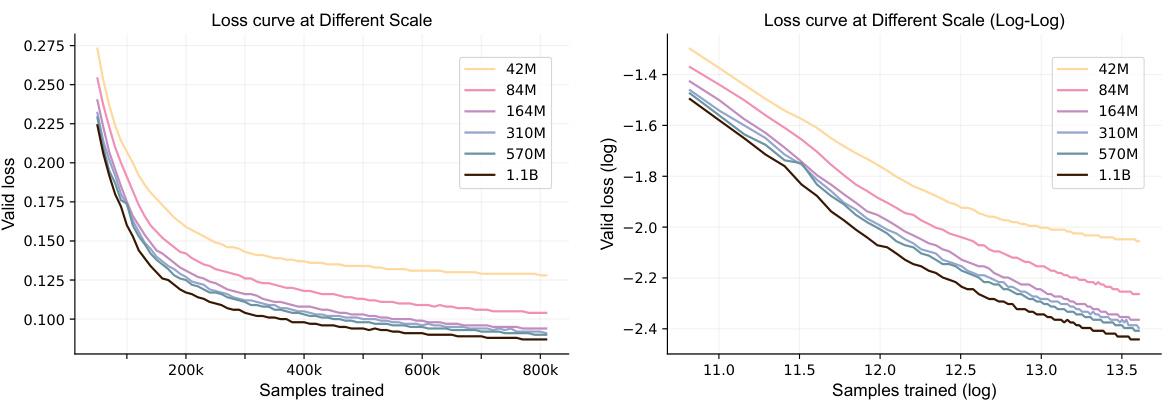
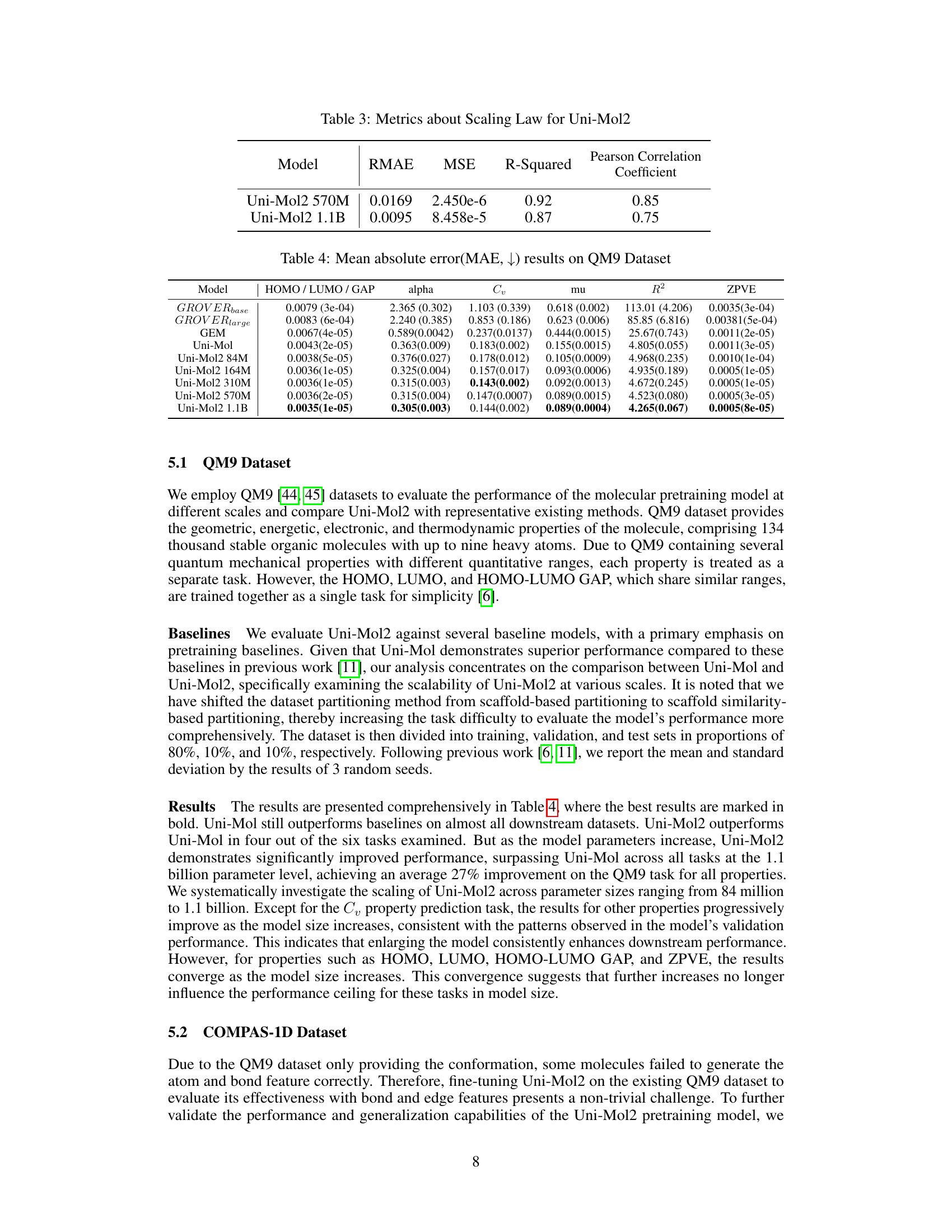
🔼 This figure displays the training curves for the Uni-Mol2 model with parameter counts varying from 42 million to 1.1 billion. The left panel shows the curves in a linear scale, highlighting the decrease in validation loss as more samples are processed and the model size increases. The right panel shows the same data using a log-log scale, making the power-law relationship between training samples and validation loss more evident. The figure also shows that at the convergence stage, the model with 84 million parameters has a validation loss of 0.105, while the 1.1 billion parameter model achieves a loss of 0.087.
read the caption
Figure 3: Validation loss curves. Training curves for Uni-Mol2 model from 42M to 1.1B parameters. Models are trained on 0.8B samples. At the convergence stage, the 84M parameters model has a loss of 0.105, and the 1.1B parameters model reaches a loss of 0.087.
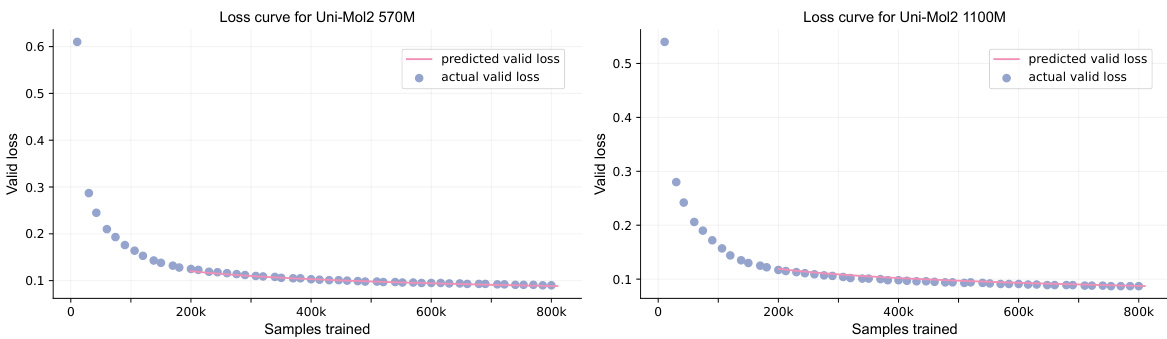
🔼 This figure displays two graphs illustrating the relationship between actual and predicted validation loss over the course of training for the Uni-Mol2 model with 570 million (left graph) and 1.1 billion (right graph) parameters. The x-axis represents the number of training samples processed, and the y-axis represents the validation loss. The graphs visually compare the model’s actual performance during training (blue dots) against a predicted validation loss (pink line), which was calculated using a power-law relationship developed in the paper. The graphs aim to demonstrate the accuracy of the proposed scaling law in predicting the model’s validation loss during training.
read the caption
Figure 4: Graph of actual loss and prediction loss across different updates for the 570M (left) and 1.1B (right) models
More on tables
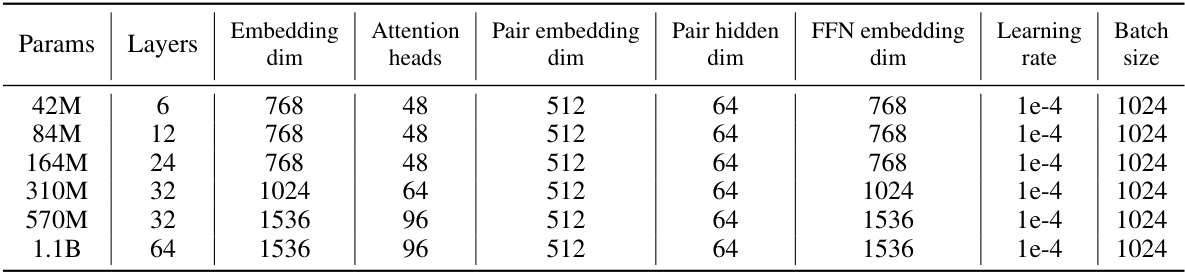
🔼 This table details the architecture of the Uni-Mol2 model at different scales, showing the number of parameters, layers, embedding dimensions, attention heads, pair embedding and hidden dimensions, FFN embedding dimensions, learning rate, and batch size for each model variant.
read the caption
Table 2: Architecture of Uni-Mol2 at different scale
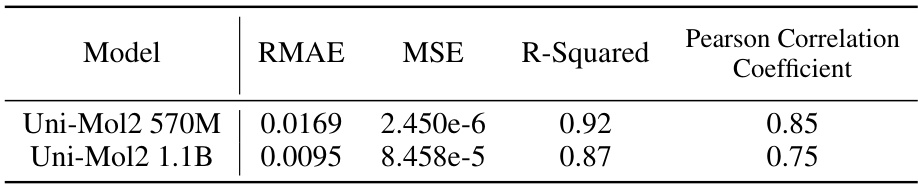
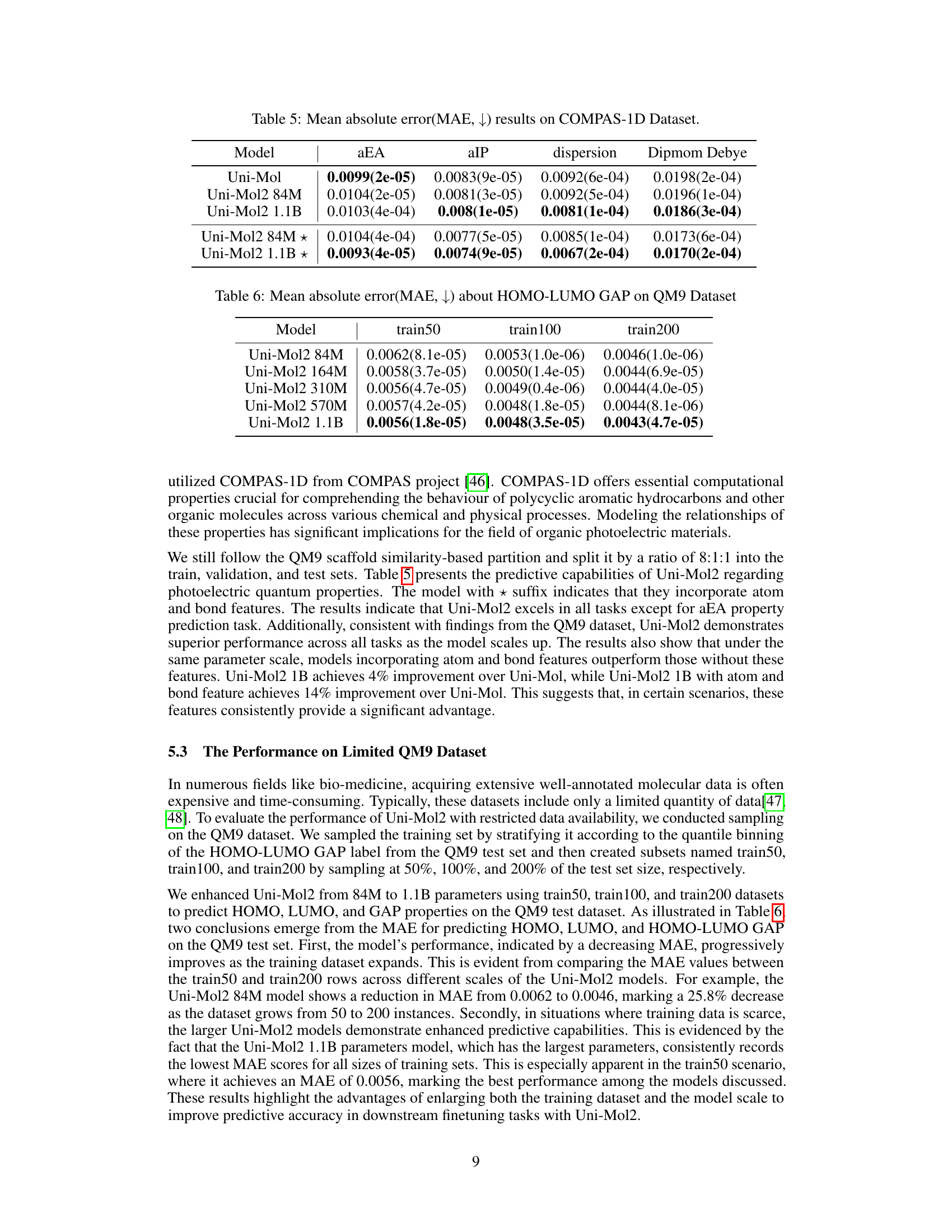
🔼 This table presents the evaluation metrics for the scaling law of the Uni-Mol2 model. It shows the Relative Mean Absolute Error (RMAE), Mean Squared Error (MSE), R-squared, and Pearson Correlation Coefficient for the 570M and 1.1B parameter versions of the model. These metrics assess how well the model’s predicted validation loss aligns with the actual validation loss across different model sizes.
read the caption
Table 3: Metrics about Scaling Law for Uni-Mol2
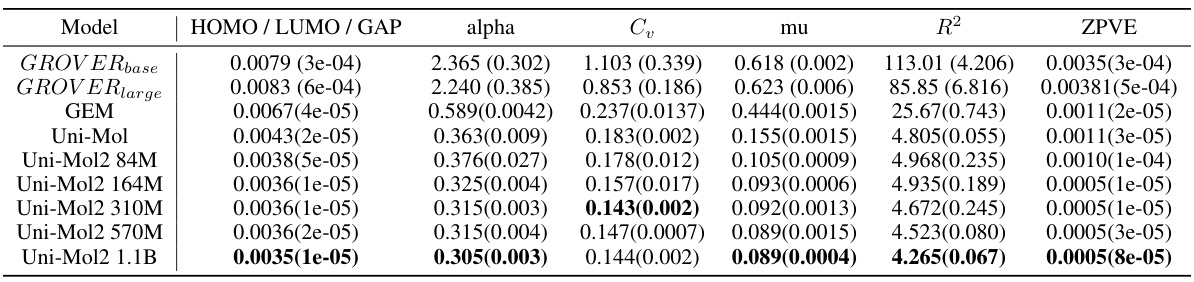
🔼 This table presents the mean absolute error (MAE) achieved by various models on the QM9 dataset. The QM9 dataset contains various quantum mechanical properties of molecules, and each property is treated as a separate task for evaluation. The table shows the performance of several baseline models (GROVERbase, GROVERlarge, GEM, Uni-Mol) and different sizes of the Uni-Mol2 model (84M, 164M, 310M, 570M, 1.1B parameters). The results are reported for the HOMO, LUMO, HOMO-LUMO gap, alpha, Cv, mu, R2, and ZPVE properties, illustrating how the accuracy improves as the model size increases.
read the caption
Table 4: Mean absolute error(MAE, ↓) results on QM9 Dataset
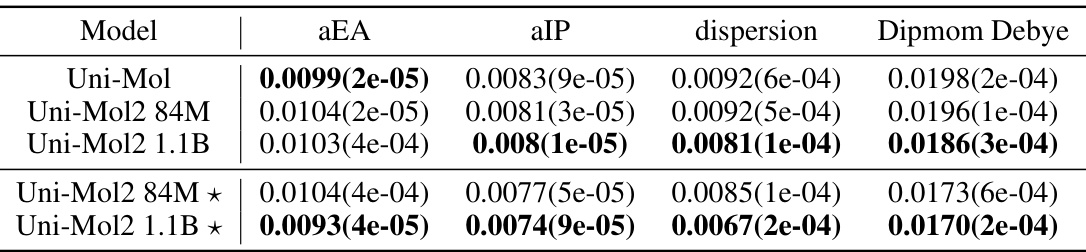
🔼 This table presents the mean absolute error (MAE) results for four different properties (aEA, aIP, dispersion, Dipmom Debye) predicted by various models on the COMPAS-1D dataset. The models include Uni-Mol, Uni-Mol2 with 84M parameters, Uni-Mol2 with 1.1B parameters, and Uni-Mol2 variants using atom and bond features. Lower MAE values indicate better performance.
read the caption
Table 5: Mean absolute error(MAE, ↓) results on COMPAS-1D Dataset.
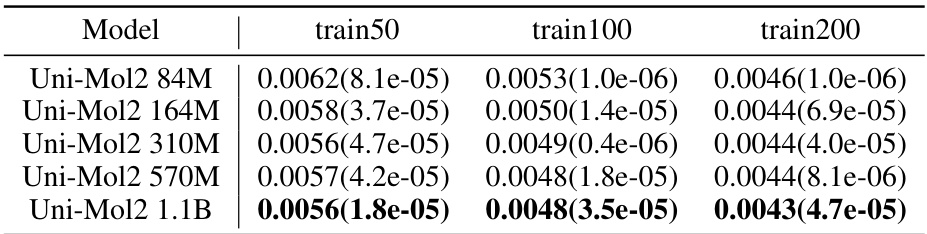
🔼 This table presents the mean absolute error (MAE) for predicting the HOMO-LUMO gap on the QM9 dataset. It shows the MAE for Uni-Mol2 models of different sizes (84M, 164M, 310M, 570M, and 1.1B parameters) trained on three different subsets of the QM9 training data (train50, train100, and train200). The results indicate how the model’s performance changes with increasing model size and training data.
read the caption
Table 6: Mean absolute error(MAE, ↓) about HOMO-LUMO GAP on QM9 Dataset
🔼 This table details the architecture of the Uni-Mol2 model at different scales, showing the number of parameters, layers, embedding dimensions, attention heads, pair embedding dimensions, pair hidden dimensions, FFN embedding dimensions, learning rate, and batch size for each model size.
read the caption
Table 2: Architecture of Uni-Mol2 at different scale

🔼 This table details the architecture of the Uni-Mol2 model at different scales, ranging from 42M to 1.1B parameters. It shows the number of parameters, layers, embedding dimensions, attention heads, pair embedding and hidden dimensions, feed-forward network (FFN) embedding dimension, learning rate, and batch size for each model variant. This allows for a comparison of model complexity across different scales.
read the caption
Table 2: Architecture of Uni-Mol2 at different scale
🔼 This table details the architecture of the Uni-Mol2 model at different scales, ranging from 42M to 1.1B parameters. For each scale, it lists the number of parameters, the number of layers, embedding dimensions, attention heads, pair embedding and hidden dimensions, FFN embedding dimension, learning rate, and batch size. These specifications provide a comprehensive overview of the model’s configuration at different sizes, enabling a comparative analysis of the scaling characteristics of the model.
read the caption
Table 2: Architecture of Uni-Mol2 at different scale

🔼 This table presents the mean absolute error (MAE) achieved by various models on the QM9 dataset. The MAE is a measure of the average absolute difference between predicted and actual values for different properties of molecules in the QM9 dataset. Lower MAE values indicate better performance. The table compares Uni-Mol2 at different scales (84M, 164M, 310M, 570M, and 1.1B parameters) against other baseline models, including GROVERbase, GROVERlarge, GEM, and Uni-Mol. Results are shown for multiple properties including HOMO, LUMO, GAP, alpha, Cv, mu, R2, ZPVE.
read the caption
Table 4: Mean absolute error(MAE, ↓) results on QM9 Dataset

🔼 This table presents the mean absolute error (MAE) of the Uni-Mol, Uni-Mol2 84M, and Uni-Mol2 1.1B models on three different ADME properties: HCLint-1, PERM-1, and SOLU-1. Lower MAE values indicate better predictive performance. The numbers in parentheses represent the standard deviation. The table shows that the 1.1B parameter Uni-Mol2 model generally achieves the lowest MAE across these three properties, suggesting improved performance with increased model scale.
read the caption
Table 11: Mean absolute error(MAE, ↓) results on Biogen ADME Dataset
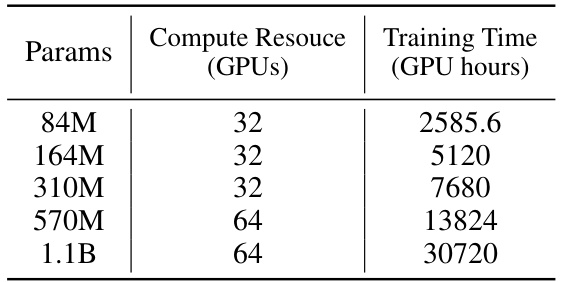
🔼 This table shows the training time (in GPU hours) and the number of GPUs used for training the Uni-Mol2 model at different scales (84M, 164M, 310M, 570M, and 1.1B parameters). It demonstrates the increasing computational cost associated with larger model sizes.
read the caption
Table 12: Training Time of Uni-Mol2 at different scale
Full paper#