TL;DR#
Spiking Neural Networks (SNNs), despite their energy efficiency, suffer from limited firing patterns due to their initial membrane potential being fixed at zero. Current SNN implementations typically use the firing rate or average membrane potential as output, limiting their potential. This paper addresses these issues.
The paper proposes a learnable initial membrane potential (IMP) to generate additional firing patterns, accelerating membrane potential evolution. It introduces a Last Time Step (LTS) approach to accelerate convergence in static tasks and a label-smoothed Temporal Efficient Training (TET) loss to address optimization-regularization conflicts. These methods yield significant accuracy improvements on ImageNet and state-of-the-art results on benchmark datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it challenges conventional assumptions in spiking neural networks (SNNs) training, leading to significant accuracy improvements. The findings offer new avenues for optimizing SNNs, enhancing their efficiency, and pushing the boundaries of neuromorphic computing. The proposed techniques are applicable across various tasks, broadening the scope of SNN applications.
Visual Insights#
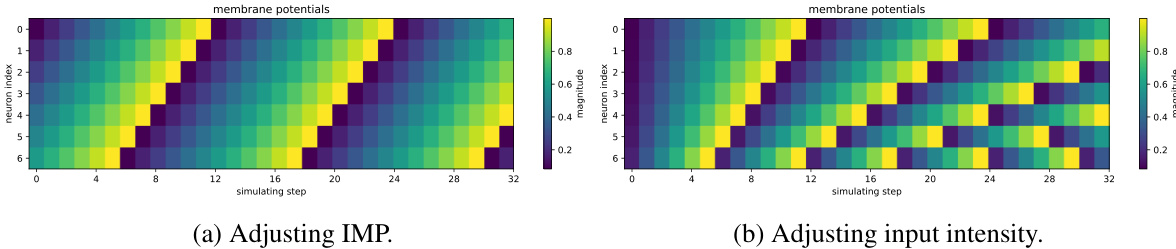
🔼 This figure shows two heatmaps visualizing membrane potentials of neurons over simulation steps. The left heatmap (a) demonstrates how adjusting the initial membrane potential (IMP) affects the membrane potential and spike generation (yellow indicates a spike). The right heatmap (b) shows a control experiment, illustrating the effect of varying input intensity while keeping the IMP constant. Comparing the two heatmaps highlights the unique impact of IMP manipulation on neuronal firing patterns.
read the caption
Figure 1: Membrane potentials and spikes (yellow) generated by adjusting IMP and input intensity.

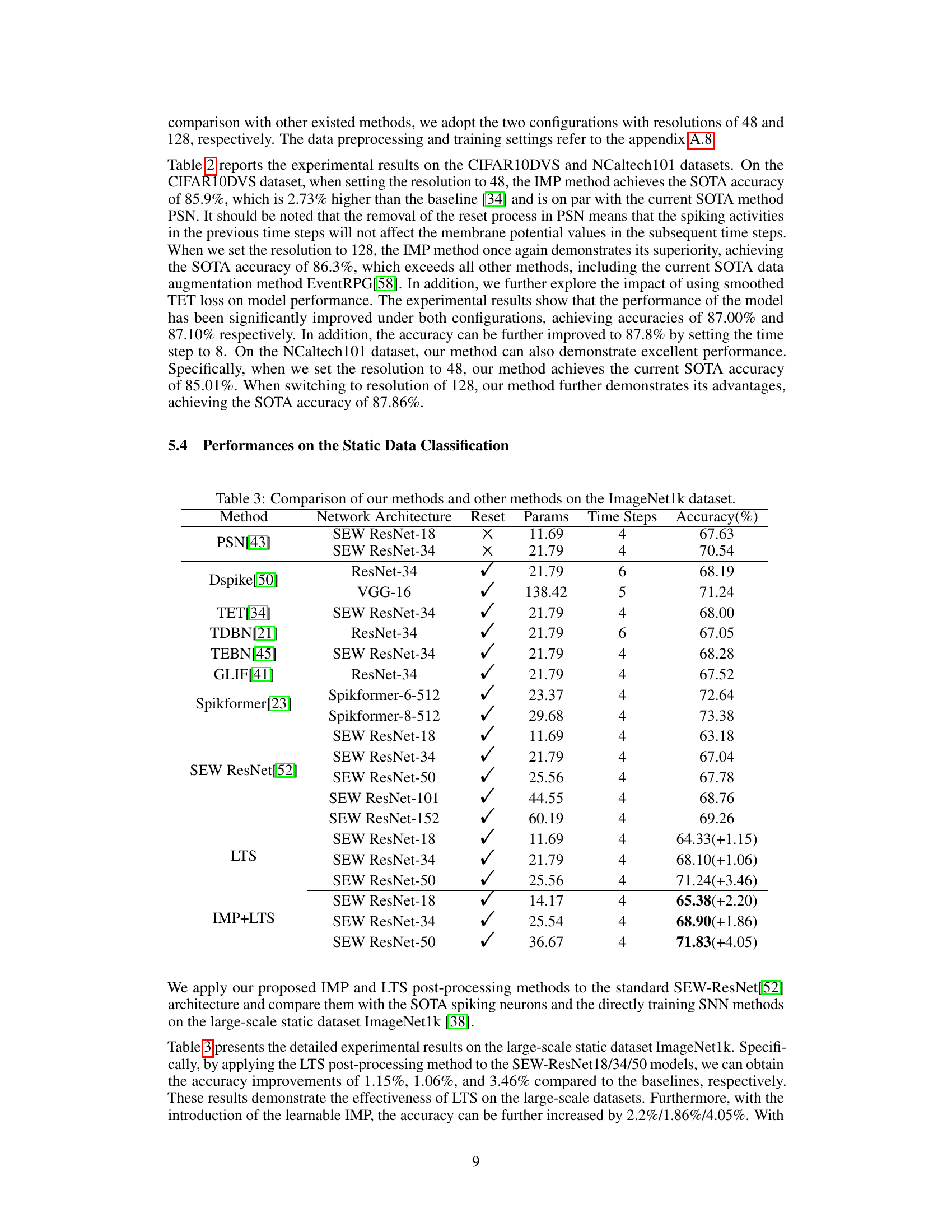
🔼 This table compares the performance of the proposed methods (IMP and IMP+TET-S) with other state-of-the-art (SOTA) methods on two neuromorphic datasets: CIFAR10-DVS and N-Caltech101. The comparison includes the SNN architecture used, input size, number of time steps, and the achieved accuracy. It highlights the superior performance of the proposed methods, especially when using the improved TET loss (TET-S).
read the caption
Table 2: Comparison of our methods and other SOTA methods on the neuromorphic datasets. Size refers to the input resolution of SNNs.
In-depth insights#
Learnable IMP#
The concept of a “Learnable IMP” (Initial Membrane Potential) offers a novel approach to enhancing spiking neural networks (SNNs). Traditionally, IMP is statically set to zero, limiting the diversity of neuronal firing patterns. By making IMP learnable, the network gains the ability to dynamically adjust the initial membrane potential of each neuron, leading to richer, more expressive spiking patterns. This directly addresses the limitation of fixed, limited spiking patterns in existing SNNs, consequently improving their representational capabilities and potentially accelerating convergence during training, especially for static tasks. The learnable IMP acts as a powerful, yet simple, mechanism to inject additional information into the SNN’s dynamics, thereby improving performance without requiring major architectural changes. This approach is biologically plausible as initial states of neurons are not always zero in real biological systems. However, further investigation is needed to explore the effects of the increased number of parameters associated with learnable IMP on computational cost, particularly for very large SNNs.
LTS for Static Tasks#
The proposed LTS (Last Time Step) method tackles the slow convergence of Temporal Efficient Training (TET) in static tasks. The core idea is that for static inputs, the SNN’s output at each time step is solely determined by the membrane potential, which evolves gradually. TET aims to optimize the accuracy at each step, leading to slow convergence. In contrast, LTS uses only the final time step’s output, significantly accelerating convergence. This is because the final time step’s membrane potential often reflects a more ‘settled’ state, effectively capturing the network’s ultimate representation of the static input, thus removing the need to optimize each intermediate representation and significantly improving the training efficiency. The combination of LTS with learnable initial membrane potential (IMP) is particularly effective as the non-zero IMP accelerates the membrane potential evolution, further enhancing performance within limited time steps.
Membrane Dynamics#
The concept of ‘Membrane Dynamics’ in spiking neural networks (SNNs) is crucial for understanding their behavior and improving performance. Membrane potential, the voltage across the neuronal membrane, is a key factor influencing the generation of action potentials (spikes), which are the basic units of information processing in SNNs. The paper explores how manipulating the initial membrane potential (IMP), usually set to 0, can significantly enhance the diversity of spike patterns generated by neurons. By adjusting the IMP, the neurons can generate additional firing patterns and pattern mappings, thus improving the expressive capacity of the network. Furthermore, the study reveals a strong correlation between membrane potential evolution and network accuracy in static tasks, highlighting the importance of efficiently driving the membrane potential towards its optimal state for improved performance. Introducing a learnable IMP accelerates this evolution, enabling higher performance within a limited number of time steps and mitigating the slow convergence issues associated with some training methods. This research therefore underscores the importance of not only the rate of spiking but also the temporal dynamics of the membrane potential for efficient and accurate SNN computation.
SNN Performance#
Spiking Neural Networks (SNNs) offer significant advantages in energy efficiency and biological plausibility compared to traditional Artificial Neural Networks (ANNs). However, SNN performance has historically lagged behind ANNs, primarily due to challenges in training and limited expressiveness of spiking neurons. This paper addresses these limitations by focusing on the membrane dynamics of SNNs. Specifically, the authors show that manipulating the initial membrane potential (IMP) of neurons unlocks more diverse firing patterns, directly impacting the information encoded and improving classification accuracy. A learnable IMP further enhances SNN performance, allowing for faster convergence and better generalization. The introduction of a Last Time Step (LTS) training approach accelerates convergence, particularly for static datasets. By mitigating conflicts between optimization and regularization, the proposed label-smoothed Temporal Efficient Training (TET) loss improves overall performance. The combined use of learnable IMP, LTS, and the improved TET loss consistently outperforms baseline methods, achieving state-of-the-art results on several benchmark datasets. Future work could explore the impact of these techniques on more complex tasks and larger-scale architectures.
Future of SNNs#
The future of Spiking Neural Networks (SNNs) is bright, driven by their inherent energy efficiency and biological plausibility. Overcoming current limitations in training and achieving performance parity with Artificial Neural Networks (ANNs) are key challenges. Improved training algorithms, such as more efficient variations of backpropagation through time, and innovative methods to address the non-differentiability of the spike function, are crucial. Exploring alternative training paradigms and leveraging neuromorphic hardware will be essential. Developing more sophisticated neuron models that capture the complexity of biological neurons and enabling learning of dynamic parameters are vital research directions. Hybrid SNN-ANN architectures might combine the advantages of both approaches. Furthermore, research into applying SNNs to novel domains such as robotics and brain-computer interfaces is likely to yield exciting advancements. Ultimately, success hinges on addressing the challenges of scalability, real-time performance, and demonstrating clear advantages over existing ANN technology.
More visual insights#
More on figures

🔼 This figure visualizes the mapping between input and output spike patterns of an Integrate-and-Fire (IF) neuron over four time steps. Each axis represents all 16 possible spike patterns (combinations of 0s and 1s over four time steps). White squares indicate successful mappings: a specific input pattern (horizontal axis) leads to a specific output pattern (vertical axis). The three subfigures (a, b, c) show how adjusting the initial membrane potential (IMP) influences the number and types of possible mappings. (a) shows the mappings with IMP set to 0.0, (b) shows it with IMP set to 0.25, and (c) with a learnable IMP. The changes demonstrate how the IMP affects the neuron’s ability to generate a diverse set of spike patterns and map input patterns to outputs.
read the caption
Figure 3: Pattern mapping of IF neuron over 4 time steps. The horizontal and vertical axes in the figure represent all possible spike patterns (16 total) that IF neurons may receive and emit. The white squares indicate that IF neuron can receive the spike pattern from the horizontal axis and emit a spike pattern on the vertical axis, known as pattern mapping.

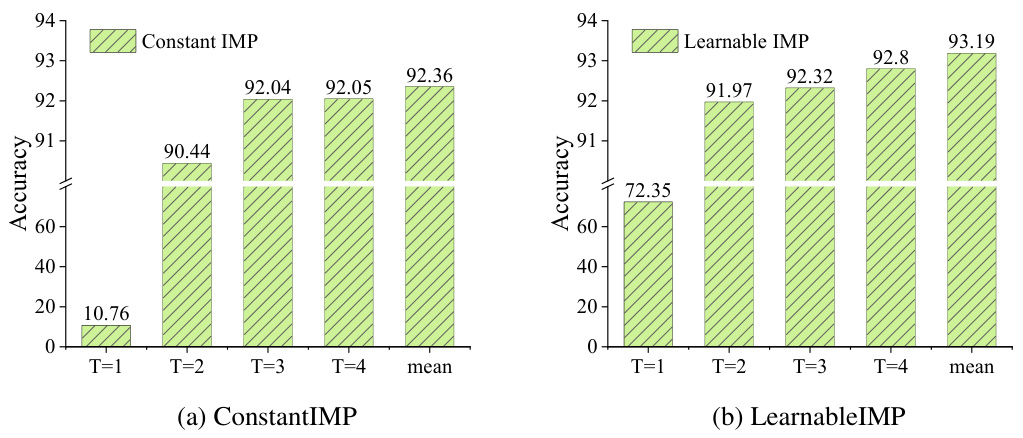
🔼 The figure shows the test accuracy of SNNs at each time step on the CIFAR10 dataset. The accuracy is extremely low at T=1 (only 10.76%). However, as the time step T increases, the model accuracy exhibits an upward trend, exceeding 90%. This illustrates the impact of the membrane potential’s evolution on SNN accuracy during the processing of static inputs. The accuracy is directly related to the membrane potential, which is the only time-varying term in static tasks.
read the caption
Figure 4: The test accuracy at each time step on the CIFAR10 dataset.

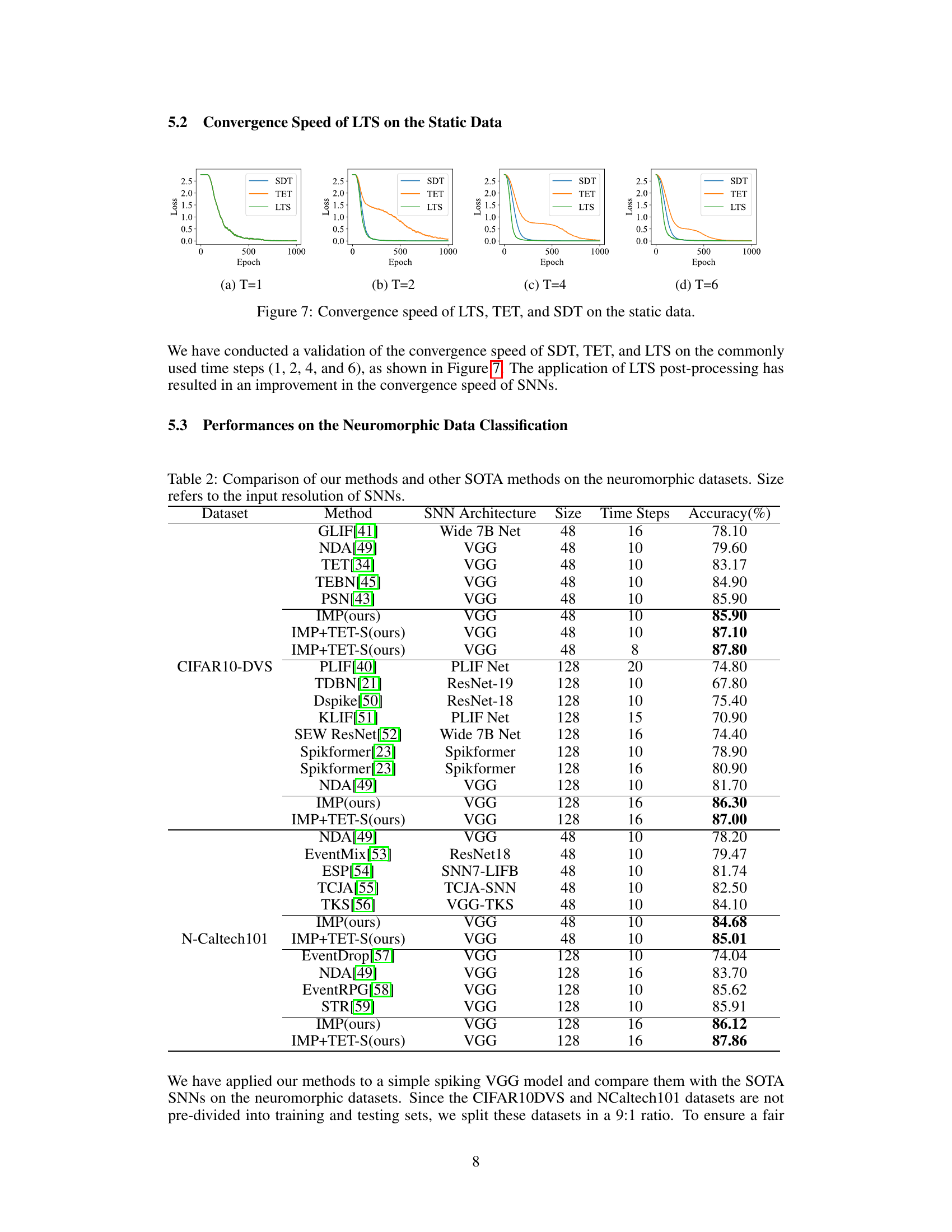
🔼 The figure shows the training loss curves for both TET and SDT loss functions across different time steps (T=1, 2, 4, and 6) on a static dataset. It illustrates that TET converges slower than SDT, especially in the initial stages of training, which is consistent with the paper’s observations about the challenges of using TET for static tasks.
read the caption
Figure 5: The convergence speed of TET and SDT on the static data.
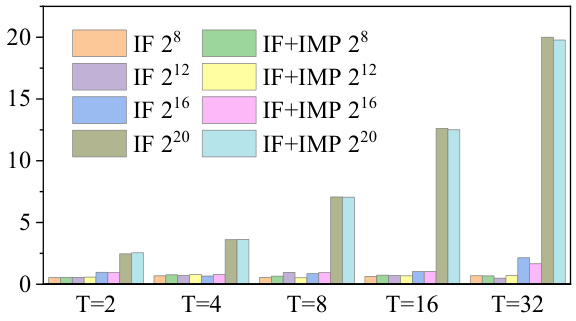
🔼 This figure compares the execution speed of the forward and backward passes between vanilla IF neurons and IF neurons with learnable IMP. Different numbers of neurons (28, 212, 216, 220) and varying time steps (2, 4, 8, 16, 32) are tested. The results show that adding learnable IMP introduces almost no difference in execution speed, indicating that the computational overhead of the IMP method is negligible.
read the caption
Figure 6: Execution time (ms) for the forward and backward pass of IF neurons, w/wo IMP.
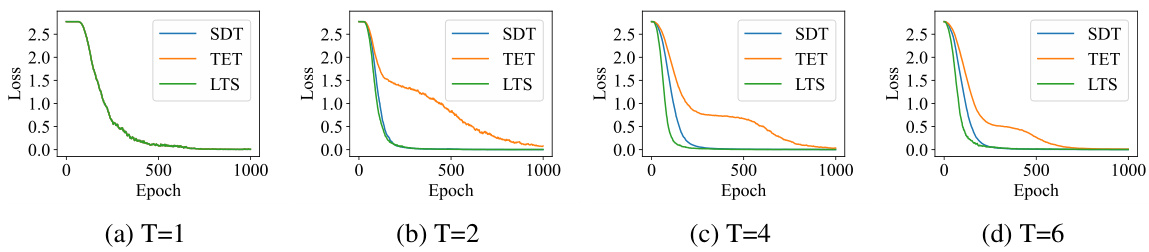
🔼 The figure shows the convergence speed of three different loss functions (SDT, TET, and LTS) on a static dataset at different time steps (T=1, 2, 4, and 6). Each subplot represents a different time step, showing the training loss plotted against the number of epochs. The plots illustrate the relative convergence speeds of the three loss functions; LTS is shown to converge faster than SDT and TET, particularly in the earlier stages of training.
read the caption
Figure 5: The convergence speed of TET and SDT on the static data.
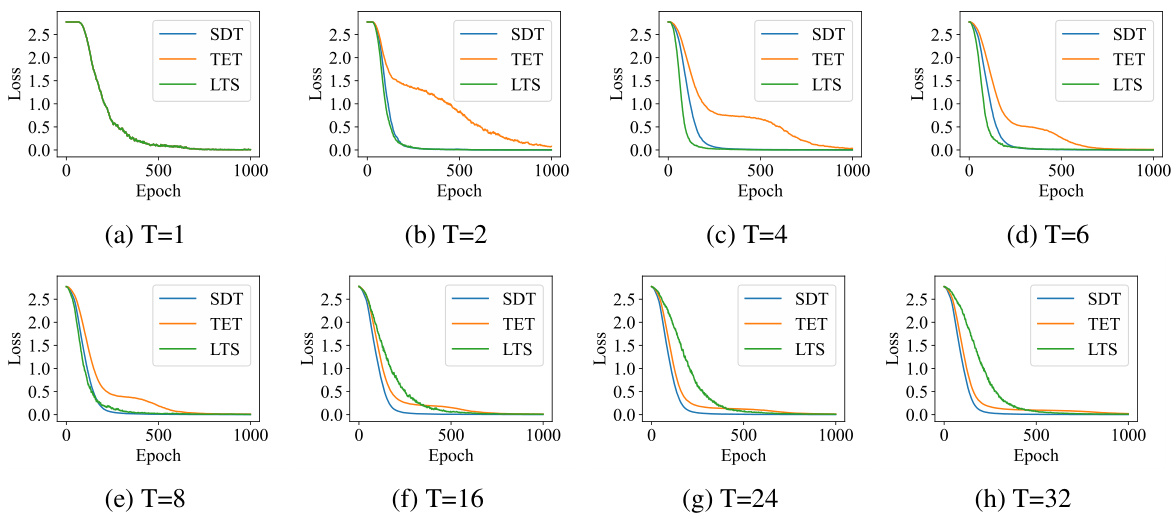
🔼 This figure shows the convergence speed of three different training methods (SDT, TET, and LTS) on static data for various time steps (T=1 to 32). Each subplot represents a different time step, displaying the loss curves over the training epochs. The curves illustrate how quickly each method’s loss decreases, thus indicating the relative speed of convergence for each training approach under different temporal settings.
read the caption
Figure 8: The convergence speed of SDT, TET and LTS on static data.
🔼 This figure shows the membrane potentials and spike patterns of a neuron under two different manipulations: adjusting the initial membrane potential (IMP) and adjusting the input intensity. It demonstrates how varying IMP leads to the generation of novel spike patterns, even with a constant input intensity. This observation is crucial to the paper’s argument for using a learnable IMP.
read the caption
Figure 1: Membrane potentials and spikes (yellow) generated by adjusting IMP and input intensity.
More on tables

🔼 This table presents the test accuracy achieved by using two different loss functions, SDT (Standard Direct Training) and TET (Temporal Efficient Training), on several datasets. The datasets are categorized into static datasets (ImageNet1k, ImageNet100, CIFAR10/100) and neuromorphic datasets (CIFAR10DVS, DVSG128, N-Caltech101). The table shows the performance of each loss function on each dataset, allowing for a comparison of their effectiveness across different types of datasets.
read the caption
Table 1: Test accuracy of TET and SDT on the static and neuromorphic datasets.
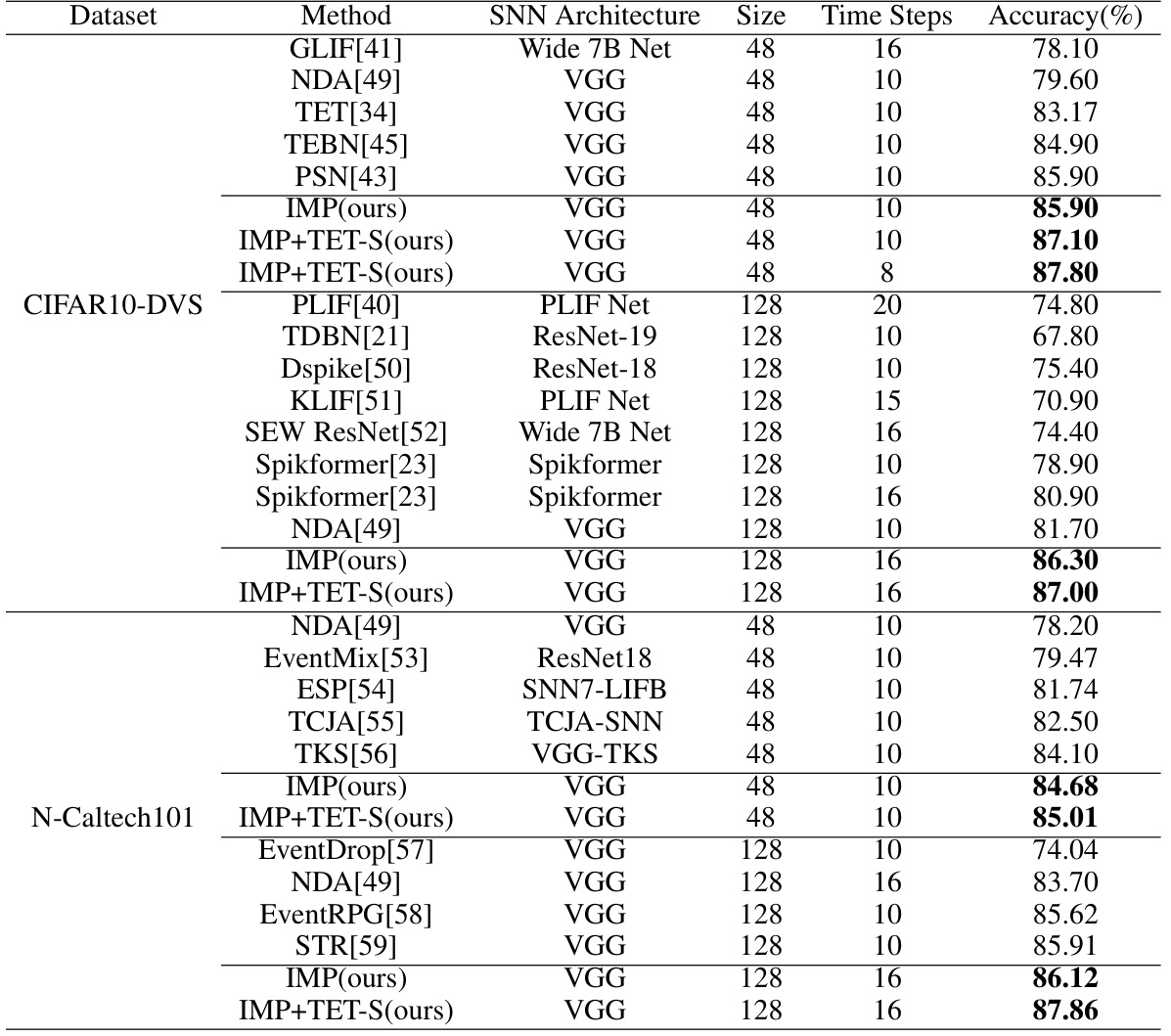
🔼 This table compares the performance of the proposed methods (IMP, IMP+TET-S) against other state-of-the-art (SOTA) methods on two neuromorphic datasets: CIFAR10-DVS and N-Caltech101. For each method, the table shows the SNN architecture used, the input size, the number of time steps, and the achieved accuracy. The results demonstrate the improved accuracy of the proposed methods, particularly IMP+TET-S, which achieves state-of-the-art performance on both datasets.
read the caption
Table 2: Comparison of our methods and other SOTA methods on the neuromorphic datasets. Size refers to the input resolution of SNNs.
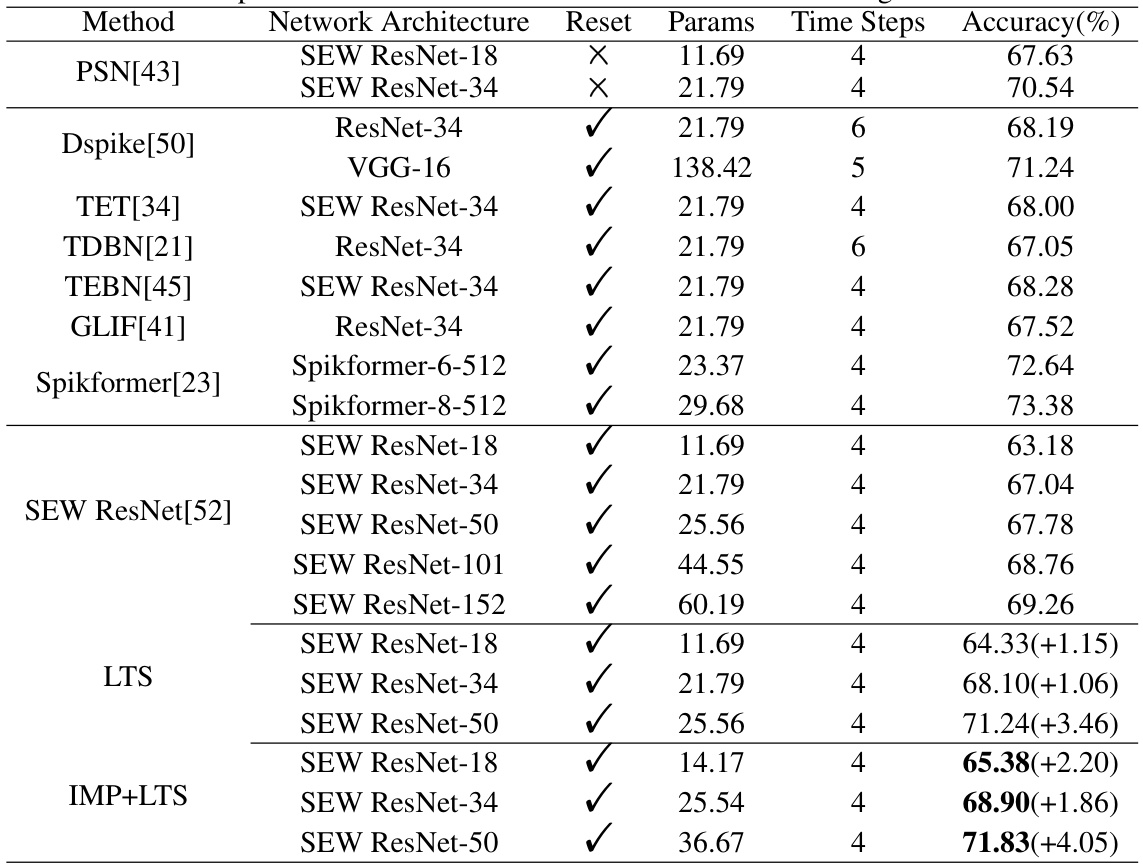
🔼 This table compares the performance of the proposed IMP+LTS method with several other state-of-the-art methods on the ImageNet1k dataset. It shows the accuracy achieved by each method using different network architectures (SEW ResNet-18, SEW ResNet-34, SEW ResNet-50, etc.), with and without the proposed improvements (IMP and LTS). The table highlights the improvement in accuracy achieved by incorporating the IMP and LTS methods.
read the caption
Table 3: Comparison of our methods and other methods on the ImageNet1k dataset.

🔼 This table presents the results of ablation studies conducted on the CIFAR10-DVS and ImageNet100 datasets. The goal was to analyze the impact of various factors (different loss functions, smoothing factors, and the learnable IMP) on model performance to understand their roles and optimize model design. The results highlight the best-performing configurations and parameter choices for each dataset.
read the caption
Table 4: Ablation Study on CIFAR10DVS and Imagenet100.
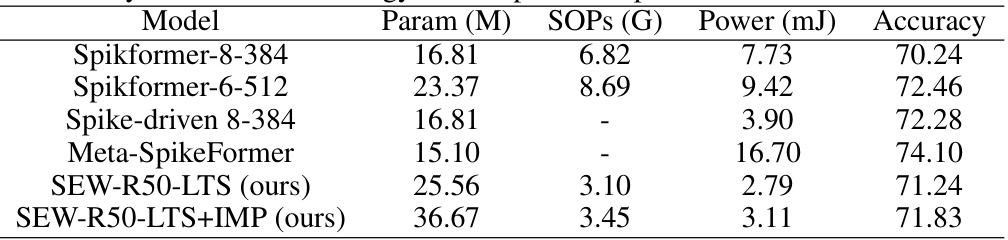
🔼 This table compares the performance of the proposed method (SEW-R50-LTS and SEW-R50-LTS+IMP) with other state-of-the-art Transformer-based spiking neural networks (SNNs). The metrics compared include the number of parameters (Param), the number of synaptic operations (SOPs), power consumption (Power), and accuracy on the ImageNet1k dataset. The results demonstrate that the proposed methods achieve competitive accuracy while maintaining relatively low computational costs and power consumption.
read the caption
Table 5: Accuracy and theoretical energy consumption compared with Transformer-based SNNs.
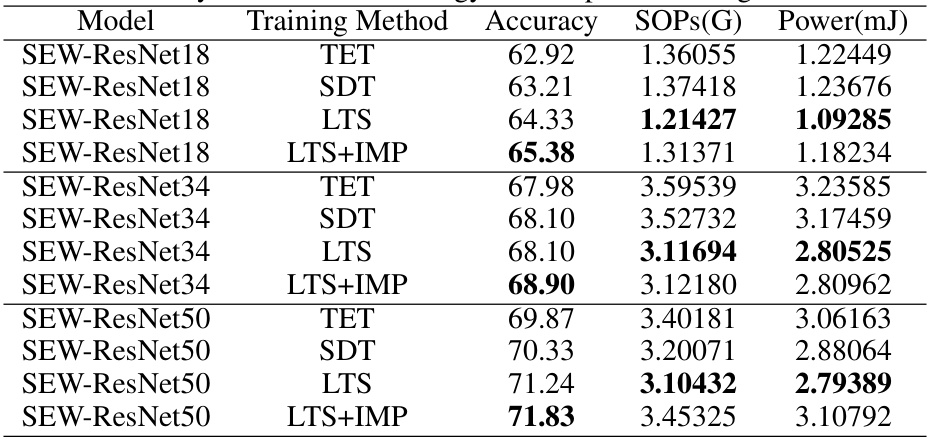
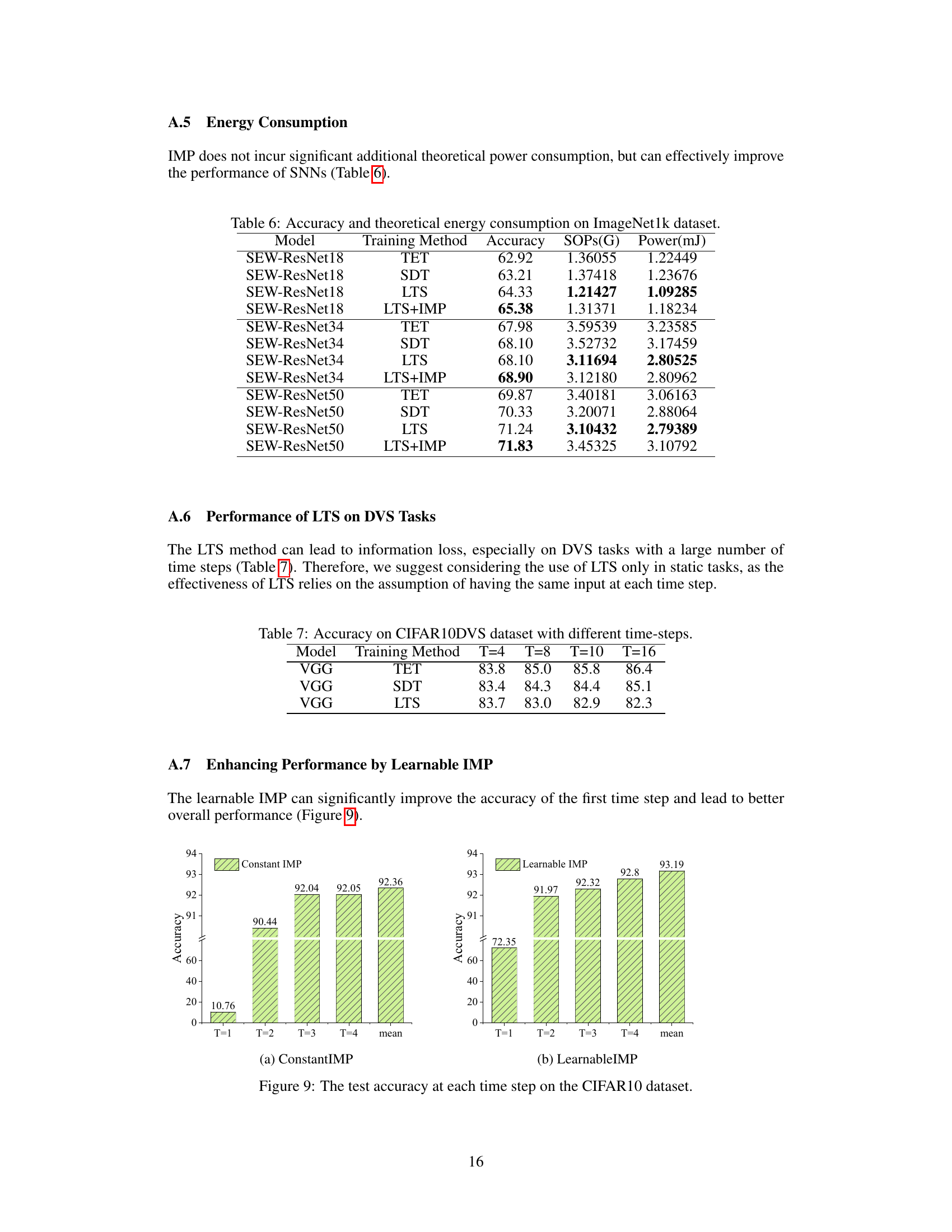
🔼 This table shows the accuracy, number of multiply-accumulate operations (SOPs), and power consumption (in millijoules) for different models (SEW-ResNet18, SEW-ResNet34, SEW-ResNet50) trained using various methods (TET, SDT, LTS, LTS+IMP). It demonstrates the impact of each training method on both accuracy and energy efficiency for different network sizes.
read the caption
Table 6: Accuracy and theoretical energy consumption on ImageNet1k dataset.

🔼 This table presents the accuracy results of three different training methods (TET, SDT, and LTS) on the CIFAR10-DVS dataset using VGG architecture with varied time steps (T=4, T=8, T=10, and T=16). It showcases how the accuracy changes with different training methods and time steps, allowing comparison of their effectiveness across different temporal resolutions.
read the caption
Table 7: Accuracy on CIFAR10-DVS dataset with different time-steps.

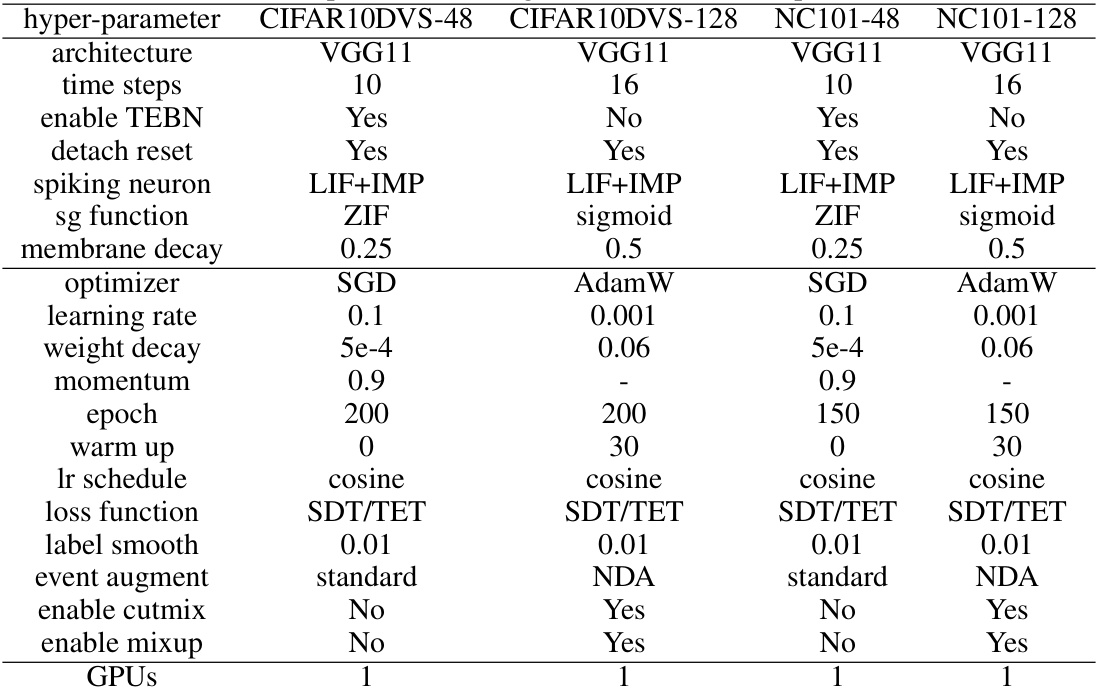
🔼 This table lists the key hyperparameters used for training on the static datasets ImageNet1k, ImageNet100, CIFAR10, and CIFAR100. It shows the architecture, number of time steps, whether temporal effective batch normalization (TEBN) was used, if the reset of the membrane potential was detached, the type of spiking neuron, the surrogate gradient function, the membrane decay, the optimizer, learning rate, weight decay, momentum, number of epochs, warm-up period, learning rate schedule, loss function, label smoothing, data augmentation methods used, and whether cutmix and mixup were enabled. The number of GPUs used for training is also indicated.
read the caption
Table 8: Experimental configurations on static task.
🔼 This table compares the performance of the proposed methods (IMP and IMP+TET-S) with other state-of-the-art (SOTA) methods on two neuromorphic datasets: CIFAR10-DVS and N-Caltech101. For each method, it lists the SNN architecture used, the input size (resolution), the number of time steps, and the achieved accuracy. The table highlights the superior performance of the proposed methods, particularly IMP+TET-S, which achieves state-of-the-art accuracy on both datasets.
read the caption
Table 2: Comparison of our methods and other SOTA methods on the neuromorphic datasets. Size refers to the input resolution of SNNs.
Full paper#