TL;DR#
Many real-world applications involve allocating limited resources among multiple agents while ensuring data privacy. Existing algorithms for such problems often lack theoretical guarantees or are computationally expensive. This poses significant challenges for researchers seeking to design efficient and privacy-preserving resource allocation mechanisms.
This paper addresses this challenge by introducing the Noisy Dual Mirror Descent (NDMD) algorithm. NDMD uses noisy mirror descent on a dual problem to coordinate allocations while maintaining differential privacy. The authors provide theoretical analysis, showing that the algorithm achieves a near-optimal balance between utility and privacy. They also derive a minimax lower bound, which confirms the algorithm’s effectiveness. Numerical experiments are conducted to validate the theoretical findings.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and resource allocation. It provides a near-optimal algorithm for solving resource allocation problems under joint differential privacy, addressing a critical gap in the literature. The minimax lower bound derived offers a strong theoretical foundation, while improved privacy analysis enhances the algorithm’s practical relevance.
Visual Insights#

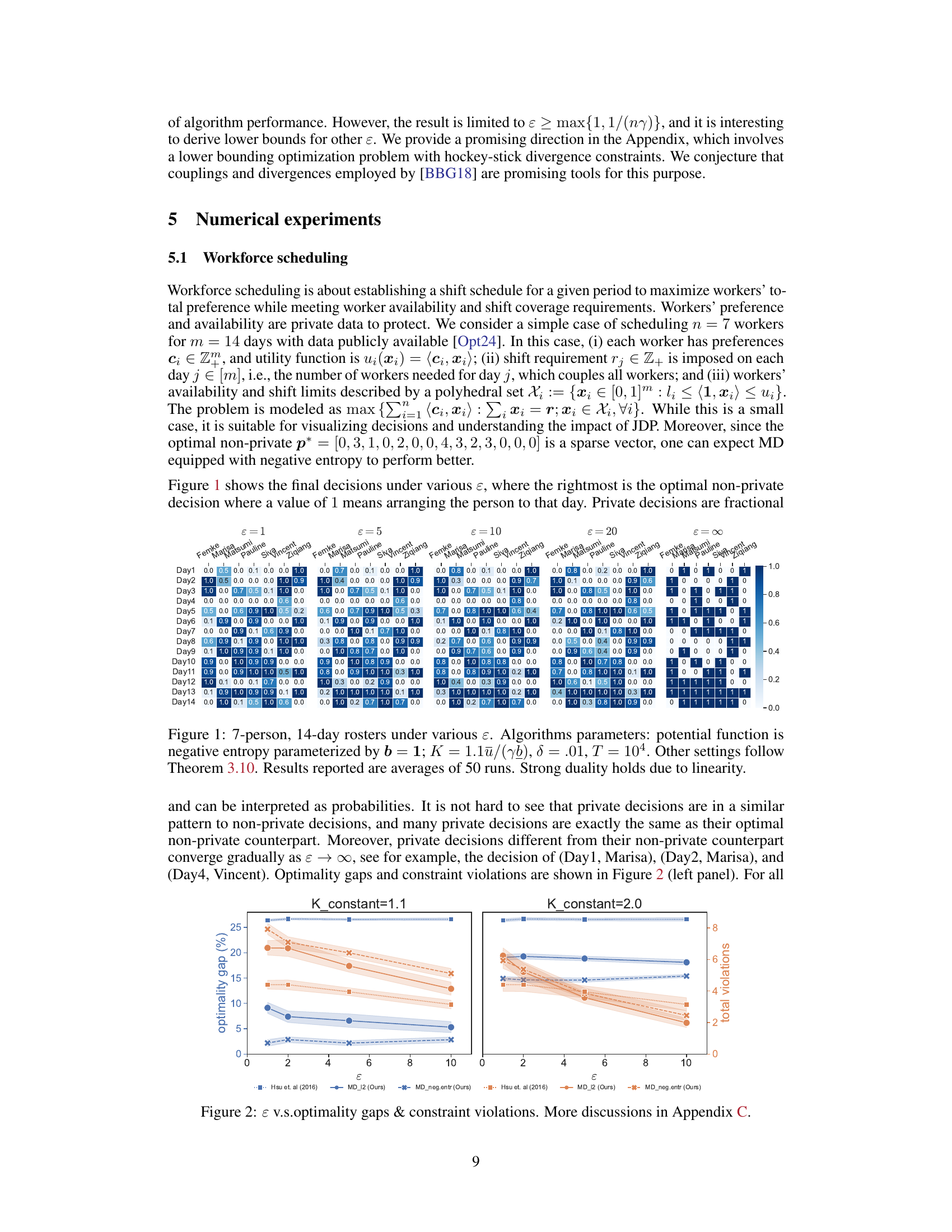
🔼 This figure shows the workforce scheduling results under different privacy levels (ɛ). Each cell in the heatmap represents the probability of assigning a worker to a specific day. The rightmost heatmap shows the optimal non-private solution, while others illustrate how the solution changes with different privacy parameters. The algorithm parameters include the potential function (negative entropy), hyperparameters (b, K, δ, T), and the number of runs.
read the caption
Figure 1: 7-person, 14-day rosters under various ɛ. Algorithms parameters: potential function is negative entropy parameterized by b = 1; K = 1.1ū/(yb), δ = .01, T = 104. Other settings follow Theorem 3.10. Results reported are averages of 50 runs. Strong duality holds due to linearity.

🔼 This table compares the theoretical results of different works on resource allocation problems under joint differential privacy. It shows the problem setup (utility function, consumption function, feasible set, and whether strong duality holds), lower bound (LB), upper bound (UB) on utility loss, and upper bound on total constraint violation for each work. The table highlights the contributions of the current work by demonstrating improvements in optimality gaps and constraint violation compared to previous works, especially under the condition of strong duality.
read the caption
Table 1: Comparison of various works on resource allocation problems under (ε, δ)-JDP.
In-depth insights#
Noisy Dual Mirror Descent#
The proposed algorithm, Noisy Dual Mirror Descent, innovatively addresses convex resource allocation problems under joint differential privacy constraints. It leverages the dual problem to introduce noise for privacy, applying noisy mirror descent to obtain private shadow prices. These prices then coordinate allocations in the primal problem, achieving near-optimal utility and low constraint violation. The algorithm’s efficiency is further enhanced by exploiting the geometric structure of the dual space when strong duality holds. Theoretical guarantees are established using Rényi differential privacy and weak duality, providing a strong theoretical foundation and confirming the algorithm’s near-optimality. Numerical experiments validate the algorithm’s effectiveness and robustness.
JDP Resource Allocation#
Joint Differential Privacy (JDP) resource allocation presents a crucial challenge in balancing privacy preservation with optimal resource distribution. The core problem lies in designing mechanisms that prevent inference of sensitive individual data from the final allocations while still achieving near-optimal utility. Strong duality in the underlying optimization problem plays a critical role in achieving better bounds on both the utility loss and constraint violations, demonstrating that leveraging the geometric structure of the dual space enhances performance. The use of Noisy Dual Mirror Descent as an algorithmic solution offers a promising approach with theoretical guarantees, though challenges remain in further tightening bounds and addressing situations where strong duality doesn’t hold. The development of minimax lower bounds provides valuable insights into the fundamental trade-offs involved. Further research should focus on extending these theoretical results to more complex scenarios and addressing the computational aspects for large-scale real-world applications.
Privacy-Utility Tradeoffs#
Analyzing privacy-utility tradeoffs in differentially private (DP) mechanisms is crucial. A core challenge is balancing the need for strong privacy guarantees (low privacy loss) with high utility (minimal information loss). Stronger privacy often reduces utility, requiring careful algorithm design and parameter tuning. This tradeoff is particularly relevant in resource allocation problems, where the goal is to maximize social welfare while protecting individual data. The optimal balance depends on the specific application, context, and risk tolerance. Quantifying this tradeoff often involves theoretical bounds, analyzing the gap between the optimal solution under no privacy constraints and the solution achieved under DP. Empirical evaluations then demonstrate the practical implications, showing how different levels of privacy affect utility in real-world scenarios. Research in this area explores novel DP techniques, enhanced analysis methods, and lower bounds to guide algorithm design and better understand the fundamental limits of privacy-preserving computation.
Minimax Lower Bounds#
Establishing minimax lower bounds is crucial for evaluating the optimality of algorithms within a specific problem domain. In the context of differentially private resource allocation, a minimax lower bound provides a benchmark against which the performance of any algorithm designed to solve this problem can be measured. It determines the fundamental limits of achievable performance considering both optimality and constraint violation, under the constraints imposed by differential privacy. A tight bound—one that closely matches existing upper bounds—demonstrates the near-optimality of the proposed algorithm, while a significant gap suggests further improvements are possible. The derivation often involves constructing a ‘hard’ instance of the problem specifically designed to foil any algorithm’s attempt to achieve superior performance, thereby highlighting the inherent difficulty associated with balancing privacy and accuracy.
Strong Duality Analysis#
Strong duality, a cornerstone of optimization theory, plays a crucial role in the performance analysis of the proposed Noisy Dual Mirror Descent algorithm. When strong duality holds between the primal and dual problems, it unlocks tighter performance bounds. The authors leverage this property to refine their optimality gap analysis, demonstrating improved convergence rates and reduced constraint violations. This improvement is particularly valuable because strong duality isn’t always guaranteed in resource allocation problems, but it often holds under reasonable conditions. The key insight lies in how strong duality shapes the geometry of the dual space, allowing for a more effective application of the Noisy Mirror Descent algorithm. The analysis meticulously demonstrates this improved performance through theoretical proofs, thereby showcasing the significance of exploiting problem-specific structures when designing differentially private algorithms. The results highlight the algorithm’s practical efficiency in situations where strong duality is satisfied.
More visual insights#
More on figures

🔼 This figure shows the impact of the hyperparameter K_constant on the performance of three different algorithms for solving the resource allocation problem under Joint Differential Privacy (JDP). The x-axis represents the privacy parameter epsilon (ε), while the y-axis on the left shows the optimality gap (the difference between the optimal objective value and the algorithm’s objective value), and the y-axis on the right shows the total constraint violations. Two different values for K_constant are shown (1.1 and 2.0). The results suggest a trade-off between optimality and constraint violation: smaller K_constant leads to lower optimality gap but higher constraint violation. Larger values of K_constant are more conservative, leading to higher optimality gaps but fewer constraint violations. The performance of the proposed algorithms (MD_12 and MD_neg.entr) is compared to the baseline algorithm (Hsu et al. 2016).
read the caption
Figure 3: K_constant v.s. optimality & constraint violations. Settings are the same as in Figure 1 except K_constant. Shadow areas and error bars indicate 95% confidence interval.
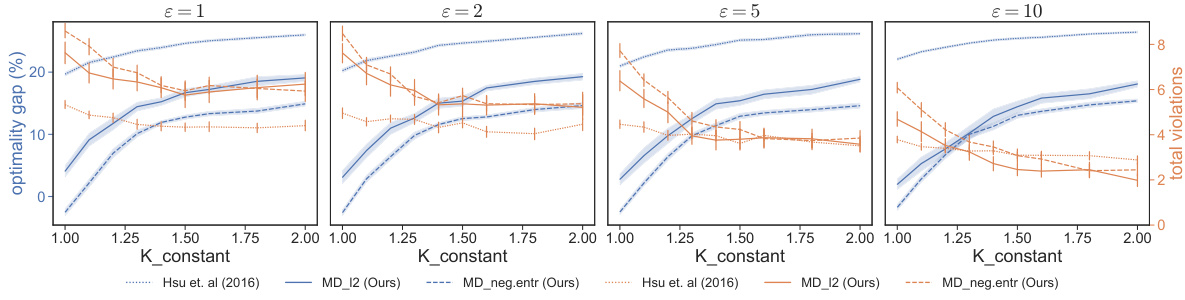
🔼 This figure shows the impact of the hyperparameter K_constant on the performance of three different algorithms for solving the resource allocation problem under joint differential privacy. The x-axis represents different values of K_constant, while the y-axis shows both the optimality gap and the total constraint violations. The figure shows that a smaller K_constant leads to a smaller optimality gap but more constraint violations, and vice versa. The trade-off between optimality and constraint violation is clearly illustrated across different values of the privacy parameter epsilon (ε).
read the caption
Figure 3: K_constant v.s. optimality & constraint violations. Settings are the same as in Figure 1 except K_constant. Shadow areas and error bars indicate 95% confidence interval.
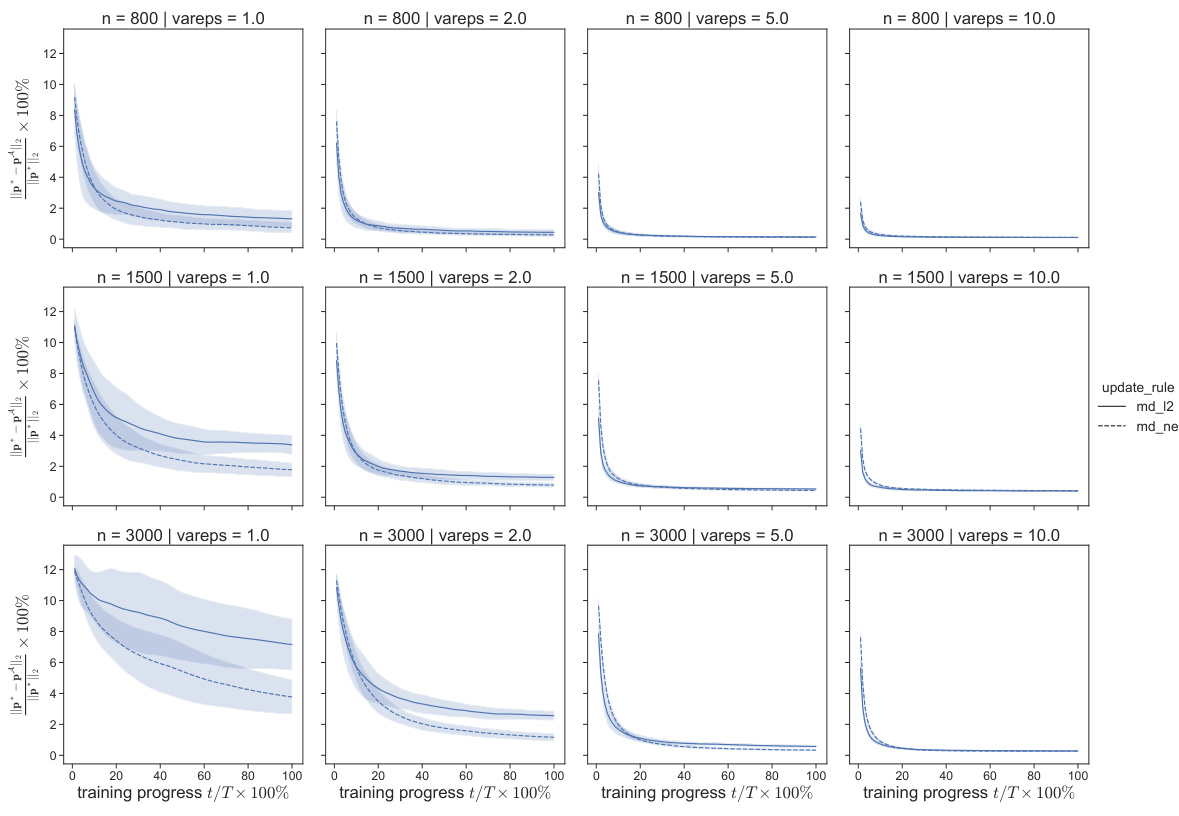
🔼 The figure shows the convergence of dual variables in the Noisy Dual Mirror Descent algorithm for different privacy parameters (ε). The y-axis represents the L2 norm of the difference between the current dual variables and the optimal dual variables, normalized by the L2 norm of the optimal dual variables. The x-axis represents the training progress. The shaded areas represent the standard deviations of the dual variables over multiple runs. The figure indicates that the convergence speed increases with larger privacy parameters (ε).
read the caption
Figure 4: (prefix averaging) dual variables converge.
More on tables

🔼 This table compares the theoretical results of different works on resource allocation problems under joint differential privacy. It shows the problem setup (utility function, consumption function, and feasible set), whether strong duality is assumed, the lower bound (LB) and upper bound (UB) on utility loss, and the upper bound on total constraint violation for each work. The table highlights the improvements achieved in the current work, such as tighter bounds and results under strong duality.
read the caption
Table 1: Comparison of various works on resource allocation problems under (ε, δ)-JDP.
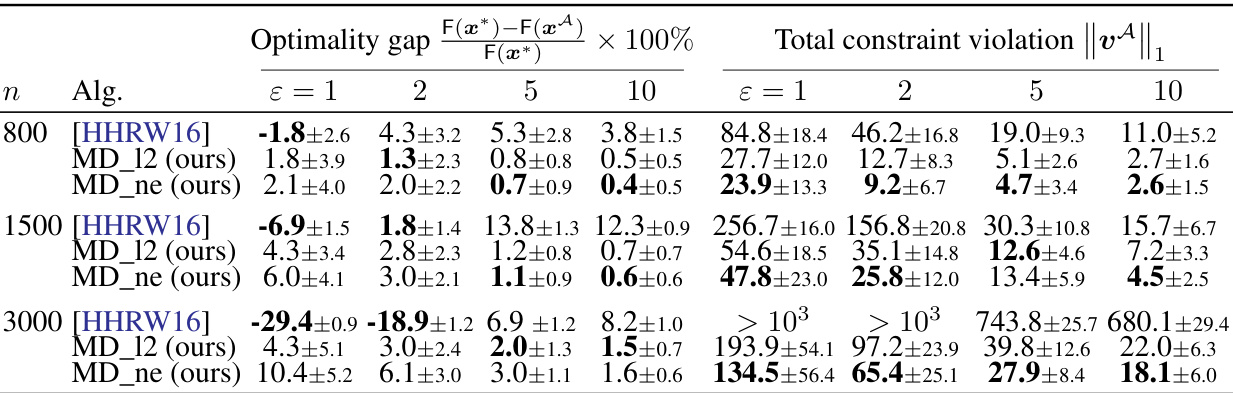
🔼 This table compares the theoretical guarantees of different algorithms for solving resource allocation problems under joint differential privacy. It shows the problem setup (utility function, consumption function, feasible set, and strong duality assumption), lower bound (LB) and upper bound (UB) on utility loss and total constraint violation for each algorithm. The algorithms are compared in terms of their optimality gap, constraint violation, and the assumptions they make. The table highlights the contributions of the proposed algorithm (Noisy Dual Mirror Descent) by comparing its performance against existing methods.
read the caption
Table 1: Comparison of various works on resource allocation problems under (ε, δ)-JDP.

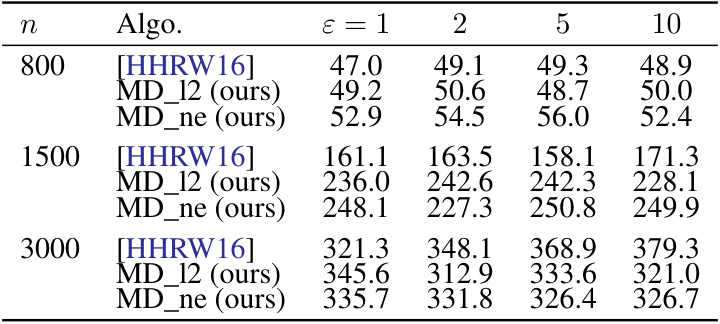
🔼 This table presents the optimality gap, calculated as (F(x*) - F(xA))/F(x*) * 100%, for three different algorithms: MD_ne (Noisy Dual Mirror Descent with negative entropy potential function), MD_12 (Noisy Dual Mirror Descent with squared l2-norm potential function), and [HHRW16], Algo 1. The results are shown for different values of epsilon (ε = 1, 2, 5, 10, 20), representing the privacy parameter. The mean and standard deviation of the optimality gap are reported for each algorithm and epsilon value.
read the caption
Table 4: Optimality gap (F(x*) – F(x^))/F(x*)×100%. mean±sd

🔼 This table compares the theoretical results of various works on resource allocation problems under (ε, δ)-joint differential privacy. It shows the problem setup (utility function, consumption function, feasible set), whether strong duality is assumed, and the upper and lower bounds for utility loss and constraint violation. The results are categorized by different algorithm approaches, highlighting the contributions of the current work compared to prior research.
read the caption
Table 1: Comparison of various works on resource allocation problems under (ε, δ)-JDP.
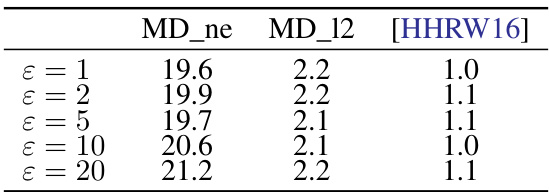
🔼 This table presents the average runtime in seconds for 1000 iterations of three different algorithms: MD_ne, MD_12, and [HHRW16] across different values of epsilon (ε). It shows the computational efficiency of each algorithm, which is a factor that impacts the algorithm’s scalability and practicality. MD_ne consistently shows the highest runtime, while MD_12 and [HHRW16] have comparable and much lower runtimes.
read the caption
Table 6: Mean runtime (in seconds) per thousand iterations

🔼 This table compares the theoretical results of different algorithms for solving resource allocation problems under joint differential privacy. It shows the problem setup (utility function, consumption function, feasible set, strong duality assumption), the lower bound (LB) and upper bound (UB) on the utility loss, and the upper bound on total constraint violation. The results from the proposed Noisy Dual Mirror Descent algorithm are compared to existing methods in the literature. It highlights the improvements achieved by utilizing the geometric structure of the dual space and strong duality.
read the caption
Table 1: Comparison of various works on resource allocation problems under (ε, δ)-JDP.
🔼 This table compares the theoretical results (utility loss upper bound, total constraint violation, and lower bound) of different algorithms for solving resource allocation problems under joint differential privacy. It shows the problem setup (utility function, consumption function, and feasible set), whether strong duality is assumed, and the theoretical guarantees of each algorithm. The algorithms considered include those proposed by Hsu et al. (2016) and by Zhang and Huang (2018), and the algorithm proposed in this paper. The table highlights the improvements in the upper bounds and the matching lower bound achieved by the proposed algorithm.
read the caption
Table 1: Comparison of various works on resource allocation problems under (ε, δ)-JDP.
Full paper#