TL;DR#
Traditional goal-conditioned reinforcement learning struggles with representing temporal goals effectively. Representations like target states are limited to simple tasks, while natural language is ambiguous. This paper tackles these issues by proposing compositional deterministic finite automata (cDFAs) as a robust and expressive goal representation. However, directly conditioning on cDFAs is challenging due to their complexity and the sparse reward signal in RL tasks. This makes learning efficient policies extremely difficult.
To overcome these challenges, the authors propose a novel approach: pre-training graph neural network embeddings on a simpler class of DFAs derived from reach-avoid tasks. This pre-training method enables zero-shot generalization to various cDFA task classes. The authors demonstrate the effectiveness of their approach through extensive experiments, showing faster policy specialization and improved performance compared to existing hierarchical methods. Their findings suggest that cDFAs combined with their pre-training method offer a promising new direction for building more adaptable and powerful goal-conditioned AI agents capable of handling complex real-world scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning and AI planning due to its novel approach to goal representation and its demonstration of strong zero-shot generalization. It addresses the limitations of existing methods by introducing compositional deterministic finite automata (cDFAs) and a pre-training method, opening new avenues for developing more flexible and robust AI agents capable of handling complex temporal tasks.
Visual Insights#
🔼 This figure illustrates the overall architecture of the proposed approach for goal-conditioned reinforcement learning using compositional deterministic finite automata (cDFAs). On the left, we see two simple deterministic finite automata (DFAs) representing individual sub-tasks. These DFAs are combined conjunctively (using an AND operation) to form a cDFA representing a more complex temporal goal. This cDFA is then fed into a graph attention network (GATv2), which produces a vector embedding of the goal. This embedding is concatenated with the agent’s current state representation (from a convolutional neural network). Finally, the concatenated vector is passed into a policy network to produce an action for the reinforcement learning agent. The image on the right is a sample illustrative environment.
read the caption
Figure 1: Given a (conjunctive) composition of deterministic finite automata (shown on the left), we construct its embedding using a graph neural network (GATv2) and use this embedding as a goal to condition the reinforcement learning policy.

🔼 This table lists the hyperparameters used for both pre-training the cDFA encoder and training the reinforcement learning policies. It includes settings for learning rate, batch size, number of epochs, discount factor, entropy coefficient, generalized advantage estimation (GAE), clipping parameter, RMSprop alpha, maximum gradient norm, and value loss coefficient. Separate hyperparameters are provided for pre-training in a dummy environment and for training in the Letterworld and Zones environments.
read the caption
Table 1: PPO pre-training and policy training hyperparameters.
In-depth insights#
cDFA for Temporal RL#
This research explores using compositional deterministic finite automata (cDFAs) to represent temporal goals in reinforcement learning (RL). cDFAs offer a compelling balance between formal expressiveness and human interpretability, making them suitable for specifying complex, temporally extended tasks. The core idea is to leverage the inherent structure of cDFAs, which are essentially Boolean combinations of simpler DFAs, to create richer goal representations than those based solely on target states or natural language descriptions. The paper proposes a novel encoding scheme for cDFAs using graph attention networks (GATv2), allowing for efficient representation and processing of these complex structures within a neural network. A key innovation is the pre-training strategy using reach-avoid derived (RAD) cDFAs, which focuses on simpler reach-avoid sub-tasks to accelerate learning and promote zero-shot generalization to unseen cDFA tasks. The empirical evaluation demonstrates the efficacy of this approach, showcasing significant improvements in both zero-shot generalization and learning speed. The experiments validate the advantage of cDFAs over simpler goal representations, highlighting their potential to unlock a new level of robustness and expressiveness in goal-conditioned reinforcement learning.
RAD-DFA Pretraining#
The heading ‘RAD-DFA Pretraining’ suggests a crucial pre-training strategy employed in the research. It leverages reach-avoid derived DFAs (RAD-DFAs), a novel concept class of DFAs, to prepare the model for handling complex goal-conditioned tasks. RAD-DFAs, unlike general DFAs, are constructed systematically, allowing for more controlled training and potentially mitigating the issues of sparsity and infinite concept classes present in raw DFAs. The pre-training likely involves learning to generate embeddings for RAD-DFAs using a graph neural network (GNN), which efficiently captures the structure of these automata. This pre-trained GNN is then fine-tuned on actual tasks, leading to faster policy specialization and improved zero-shot generalization across varying task complexities. The success of this approach hinges on the hypothesis that RAD-DFAs are simpler to learn and represent a suitable proxy to the complexities of real-world temporal goals encoded by DFAs. The effectiveness of RAD-DFA pretraining is a key aspect to be evaluated experimentally, demonstrating the feasibility and benefits of this approach in goal-conditioned reinforcement learning.
GATv2 Encoding#
The heading ‘GATv2 Encoding’ suggests a method using the Graph Attention Network version 2 (GATv2) to create vector representations of compositional deterministic finite automata (cDFAs). This encoding is crucial because it transforms the complex, symbolic structure of cDFAs into a numerical format suitable for reinforcement learning (RL) agents. The process likely involves treating the cDFA as a graph, where nodes represent states and edges represent transitions, with edge features potentially encoding transition symbols or probabilities. GATv2’s attention mechanism would then weigh the importance of different nodes and edges in the graph, capturing the inherent structure and semantics of the cDFA. The resulting embedding would serve as a goal representation for the RL agent, allowing the agent to learn policies conditioned on the temporal goals specified by the cDFA. The effectiveness of this method hinges on the ability of GATv2 to learn meaningful representations that capture the essential aspects of the cDFA’s structure, enabling zero-shot generalization to various cDFA tasks. Furthermore, the choice of GATv2 likely reflects its strengths in handling graph-structured data and its ability to learn complex relationships between nodes, essential for encoding the intricate logical structure of cDFAs.
Zero-Shot Generalization#
Zero-shot generalization, a remarkable capability, signifies a model’s ability to perform tasks unseen during training. This is particularly valuable in reinforcement learning where the space of possible tasks can be vast and unexpected. The paper investigates zero-shot generalization within the context of goal-conditioned reinforcement learning, focusing on the representation of temporal goals using compositional deterministic finite automata (cDFAs). The key innovation lies in pre-training a graph neural network (GNN) encoder on a carefully designed distribution of reach-avoid derived (RAD) DFAs. This pre-training step acts as a crucial foundation for enabling the model to learn the structural properties of DFAs, essentially teaching it to understand the underlying logic of these automata. As a consequence, the model exhibits strong zero-shot generalization to various cDFA task classes, demonstrating a significant leap in performance and efficiency compared to conventional methods. The effectiveness of this pre-training strategy is empirically validated through experiments in both discrete and continuous environments, showcasing the robustness and widespread applicability of this approach. The success underscores the power of embedding learning, leveraging structural information inherent within the task representation to achieve remarkable generalization capabilities.
Limitations of cDFA#
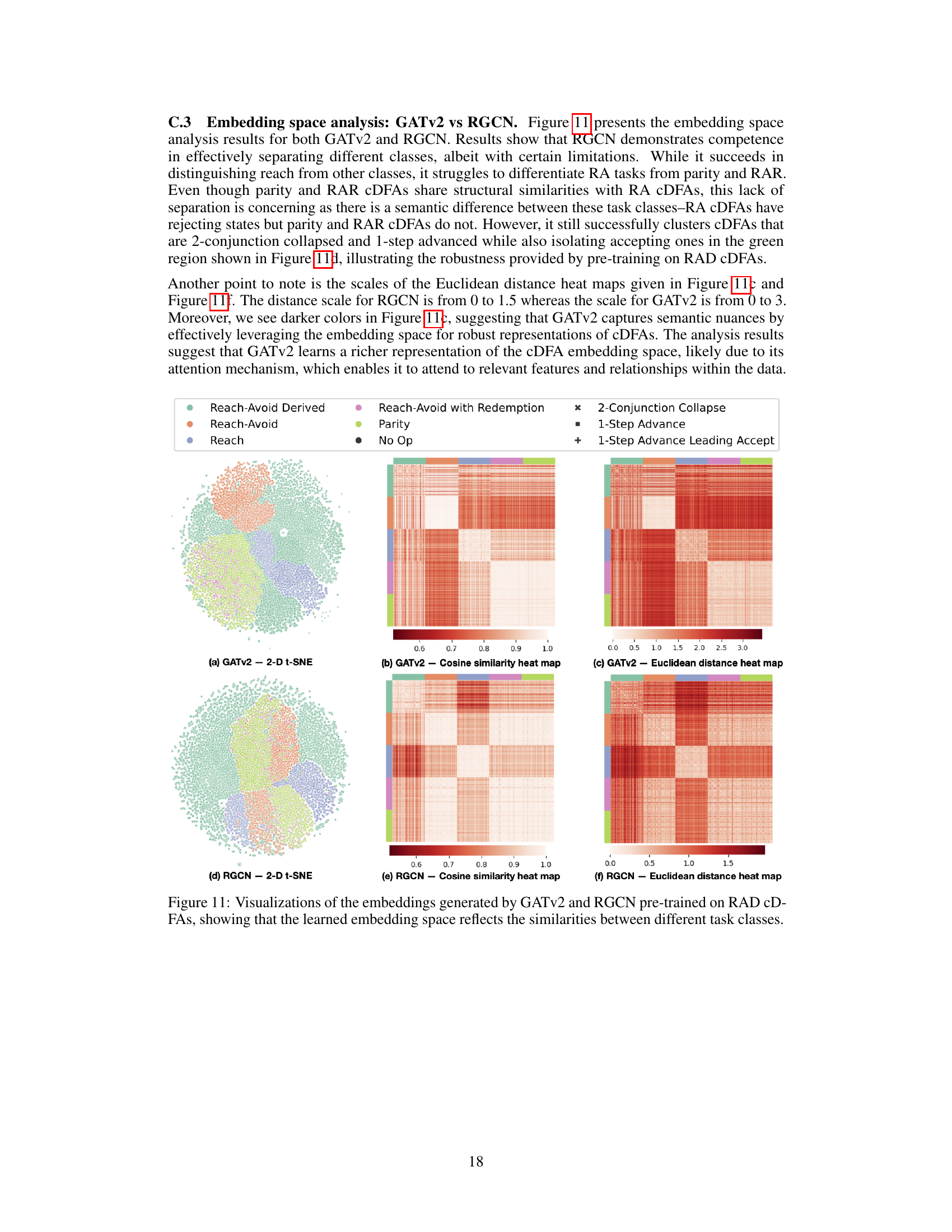
Compositional deterministic finite automata (cDFA) offer a powerful way to represent temporal goals in reinforcement learning, balancing formal semantics with interpretability. However, cDFAs present limitations. Their countably infinite and exponentially growing concept class poses challenges for generalization, as subtle changes in automaton structure can dramatically alter task semantics. This necessitates learning robust and generalizable embeddings, preventing reliance on simple pattern matching and demanding sophisticated encoding mechanisms like graph neural networks. Reward sparsity is another key limitation; the binary nature of DFA acceptance (accepting or rejecting) provides limited feedback for reinforcement learning, especially in complex environments. This is further compounded by the exponential growth of monolithic DFAs when combining multiple automata, leading to computational challenges for encoding and processing high-level tasks. Addressing these limitations requires innovative pre-training strategies and efficient encoding techniques, as demonstrated by the use of reach-avoid derived DFAs (RAD) and graph attention networks in the paper. Finally, the reliance on Boolean combinations might overlook subtleties of natural language, leading to potential misinterpretations of goals. Careful consideration of these limitations is key to leveraging the full potential of cDFAs in reinforcement learning.
More visual insights#
More on figures
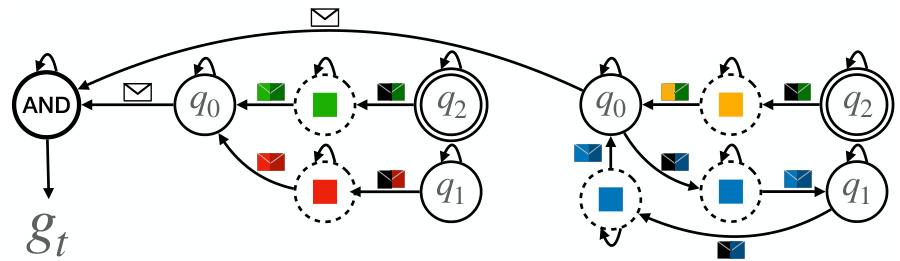
🔼 This figure illustrates the architecture for goal-conditioned reinforcement learning using compositional deterministic finite automata (cDFAs). On the left, we see a composition of multiple DFAs, each representing a sub-task. These DFAs are combined conjunctively (AND). A graph neural network (GATv2) processes this structure, generating an embedding that captures the overall goal. This embedding is then used to condition a reinforcement learning policy, enabling the agent to achieve the complex goal represented by the composed DFAs. The right side shows the embedding process and how it conditions the policy network.
read the caption
Figure 1: Given a (conjunctive) composition of deterministic finite automata (shown on the left), we construct its embedding using a graph neural network (GATv2) and use this embedding as a goal to condition the reinforcement learning policy.
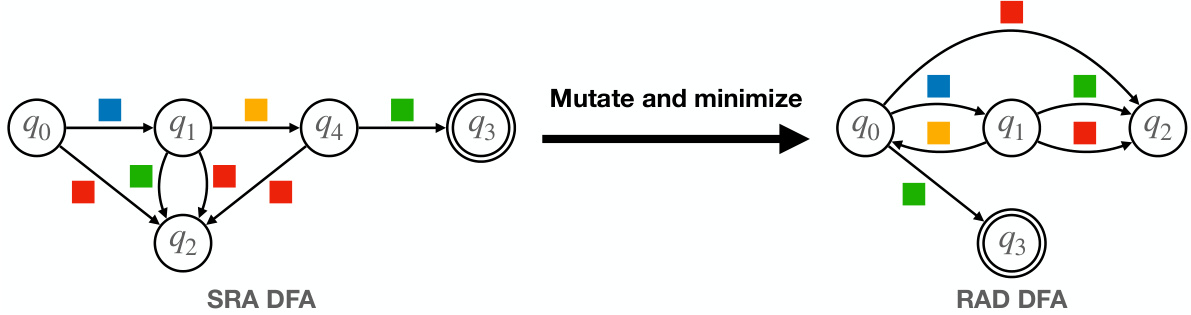
🔼 This figure illustrates the process of generating a Reach-Avoid Derived (RAD) DFA from a simpler Sequential Reach-Avoid (SRA) DFA. An SRA DFA is a DFA where paths correspond to a series of reach-avoid tasks. The figure shows an example SRA DFA, which is then mutated (a transition is randomly changed). After the mutation, the accepting state’s outgoing edges are removed and the resulting DFA is minimized. This mutated and minimized DFA is then considered a RAD DFA. The process demonstrates how a RAD DFA is a generalization of SRA DFAs, and incorporates a higher level of complexity and structure than a simple SRA DFA.
read the caption
Figure 3: An example of a sequence of local reach-avoid problems and a RAD DFA obtained from it.
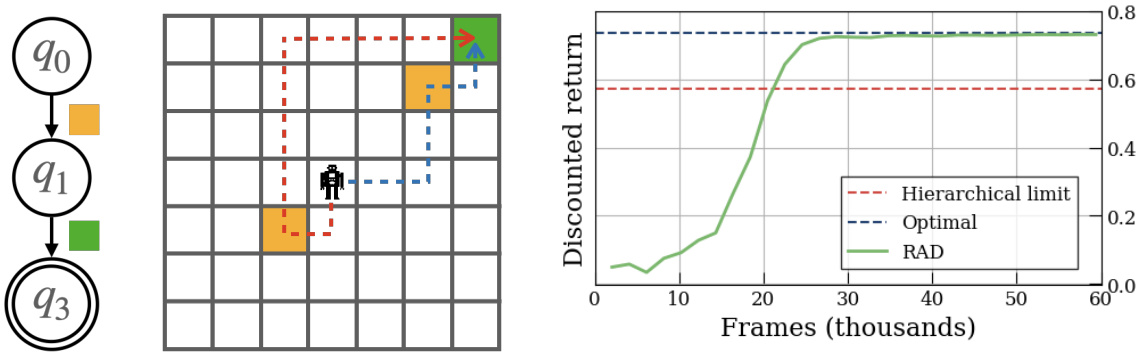
🔼 The figure shows a comparison between hierarchical reinforcement learning methods and the proposed method for solving a goal-conditioned task in a grid-world environment. The task involves reaching an orange square first and then a green square. Hierarchical approaches, due to their myopic nature, might choose a closer orange square that ultimately leads to a suboptimal path to the green square. The proposed method, by considering the entire task from the start, finds the optimal path.
read the caption
Figure 4: An example in which the myopia of hierarchical approaches causes them to find a suboptimal solution. If the task is to first go to orange and then green, the hierarchical approaches will choose the closest orange which takes them further from green whereas our approach finds the optimal solution.
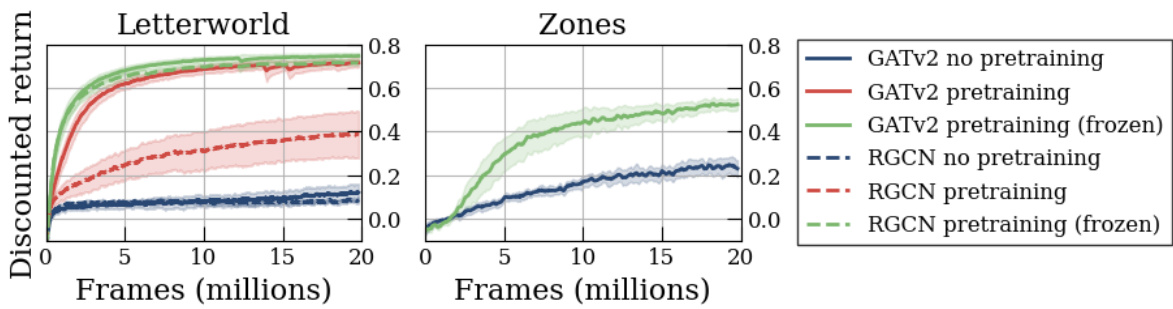
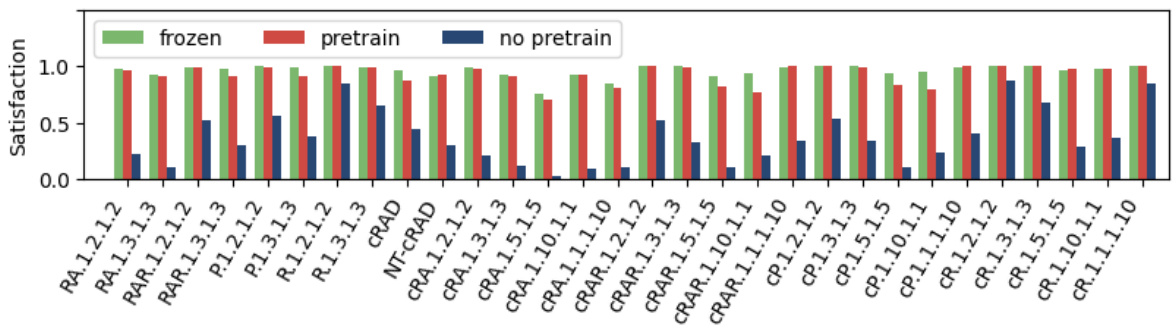
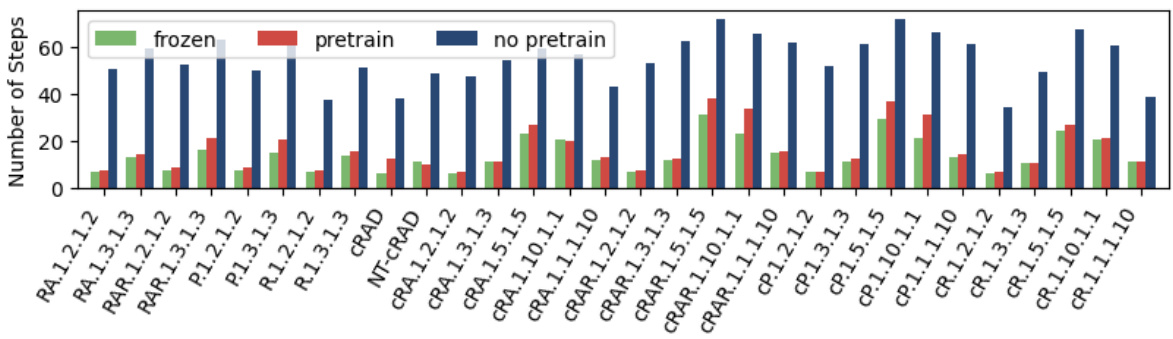
🔼 This figure compares the training performance of reinforcement learning policies trained with different methods on two environments: Letterworld (discrete) and Zones (continuous). The training curves show the discounted return achieved over time. Different lines represent different training approaches: * No pretraining: Policies trained without any pre-training on cDFAs. * Pretraining: Policies trained with pre-training on reach-avoid derived (RAD) cDFAs, where the encoder is fine-tuned during policy training. * Pretraining (frozen): Policies trained with pre-training on RAD cDFAs, but the encoder is frozen (weights are not updated) during policy training. The results indicate that pre-training significantly improves performance, especially when the encoder’s weights are frozen after pre-training. This suggests that pre-training effectively learns a good representation of the cDFAs, which can then be used to accelerate policy learning without needing to re-learn the cDFA representation during the reinforcement learning process.
read the caption
Figure 5: Training curves (error bars show a 90% confidence interval over 10 seeds) in Letterworld (discrete) and Zones (continuous) for policies trained on RAD cDFAs, showing that frozen pre-trained cDFA encoders perform better than non-frozen ones while no pre-training barely learns the tasks.
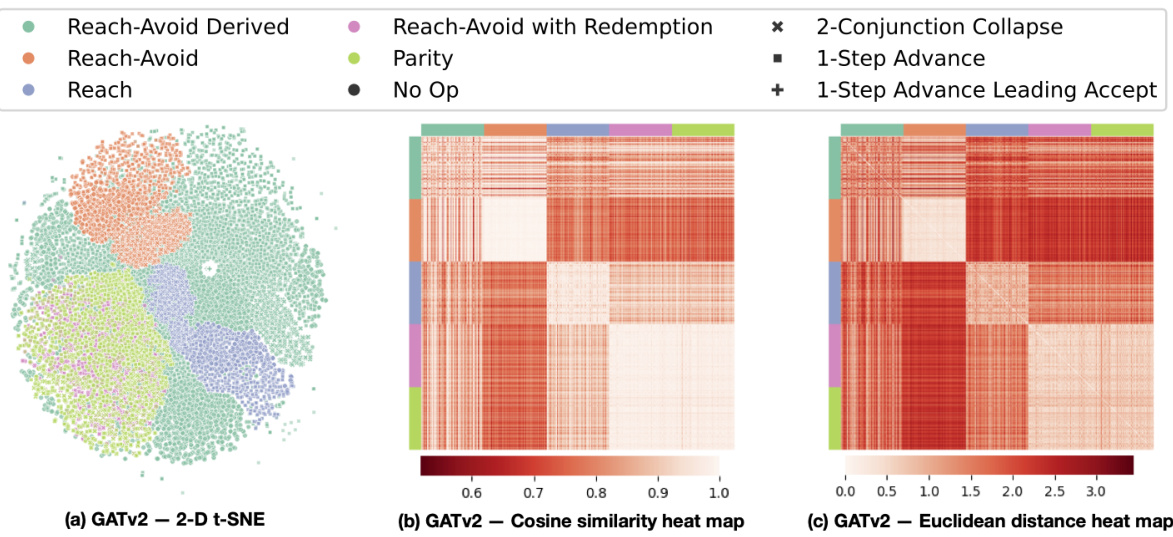
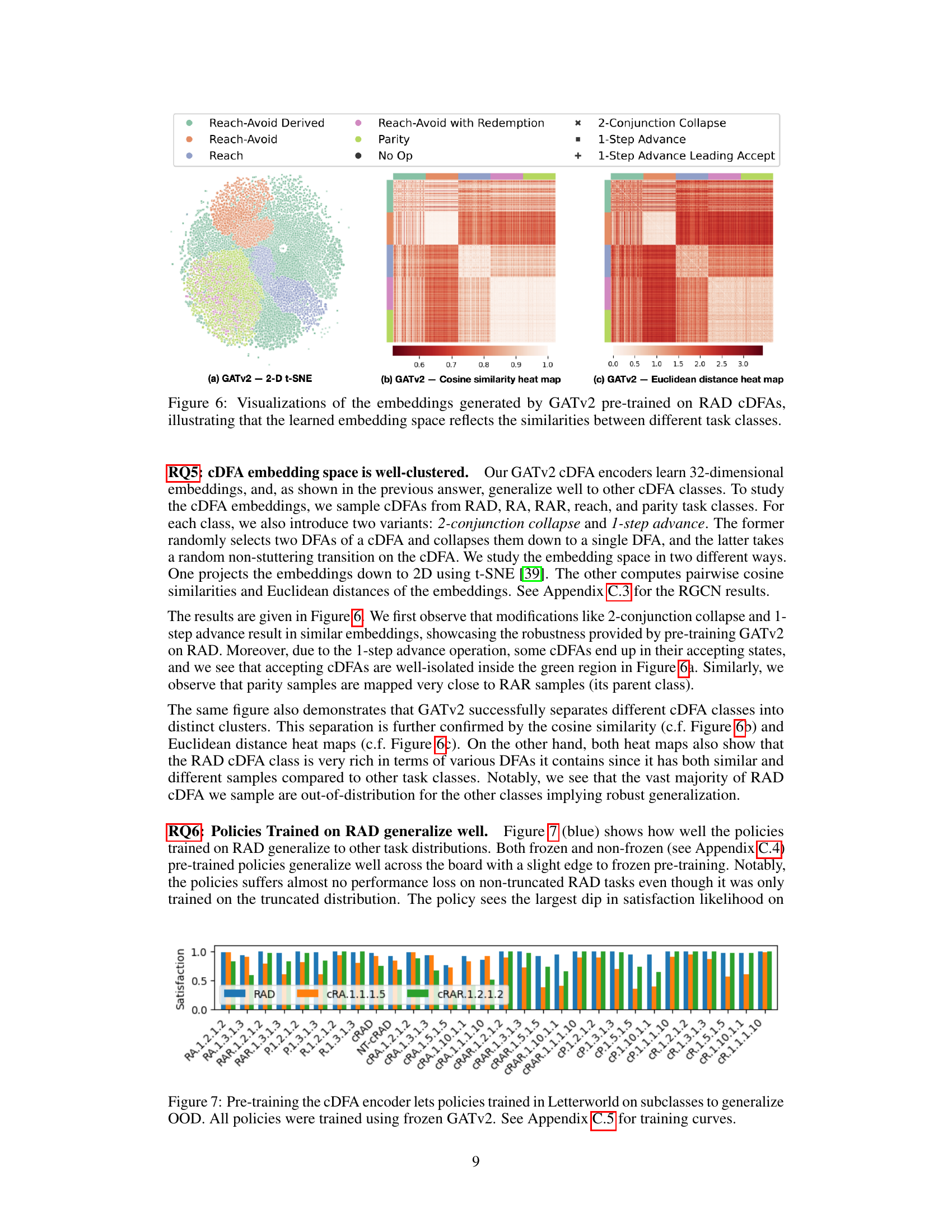
🔼 This figure visualizes the embedding space generated by the Graph Attention Network (GATv2) model pre-trained on Reach-Avoid Derived (RAD) compositional deterministic finite automata (cDFAs). It uses three different visualization techniques to show how well the model clusters different cDFA task classes in its embedding space. Panel (a) shows a 2D t-SNE projection of the 32D embeddings, clearly showing distinct clusters for different task types. Panels (b) and (c) present heatmaps of cosine similarity and Euclidean distance between all pairs of cDFA embeddings, respectively. The heatmaps further confirm the clustering observed in the t-SNE plot and highlight the relationships between different task complexities. The figure demonstrates that GATv2 effectively learns a meaningful representation of cDFAs that captures their structural and semantic similarities.
read the caption
Figure 6: Visualizations of the embeddings generated by GATv2 pre-trained on RAD cDFAs, illustrating that the learned embedding space reflects the similarities between different task classes.
🔼 This figure illustrates the overall architecture of the proposed approach. A composition of deterministic finite automata (cDFA) is used to represent temporal goals. A graph attention network (GATv2) is used to generate an embedding vector from the cDFA. This embedding vector is then used as an input to condition a reinforcement learning policy network, which outputs actions to the agent in the environment.
read the caption
Figure 1: Given a (conjunctive) composition of deterministic finite automata (shown on the left), we construct its embedding using a graph neural network (GATv2) and use this embedding as a goal to condition the reinforcement learning policy.

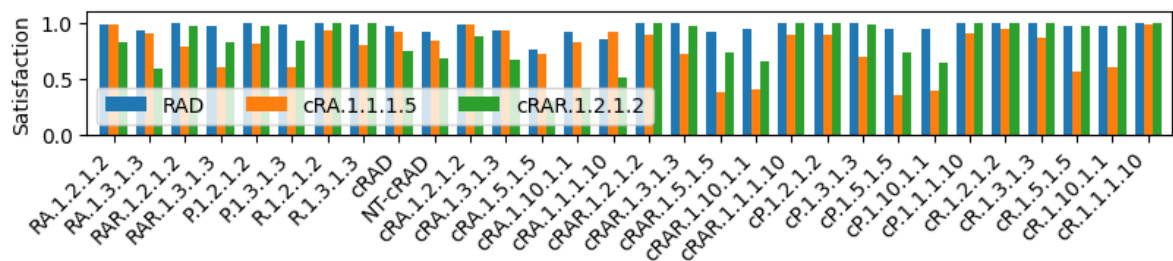
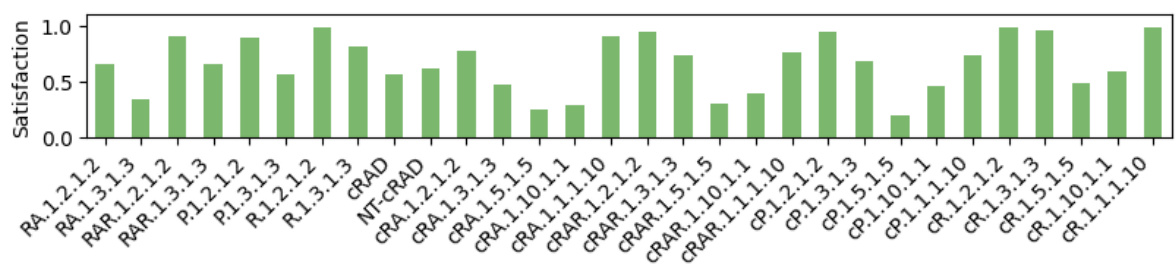
🔼 This figure compares the generalization capabilities of policies trained using two different methods on various LTL tasks. The first set of policies were trained by the LTL2Action approach ([38]), while the second set were trained using the RAD CDFA method described in this paper. The figure shows the satisfaction rate (or success rate) for each policy on a range of LTL tasks. The Appendix C.8 provides further details on the training curves for each set of policies.
read the caption
Figure 8: Satisfaction generalization capabilities on LTL tasks (from [38]) of LTL2Action [38] policies vs policies trained on RAD CDFAs. See Appendix C.8 for training curves of policies.
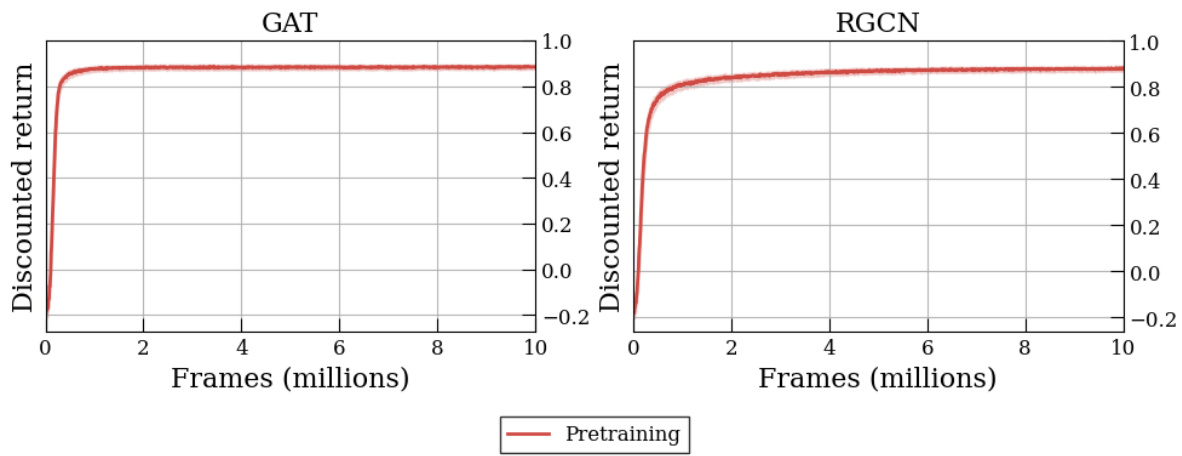
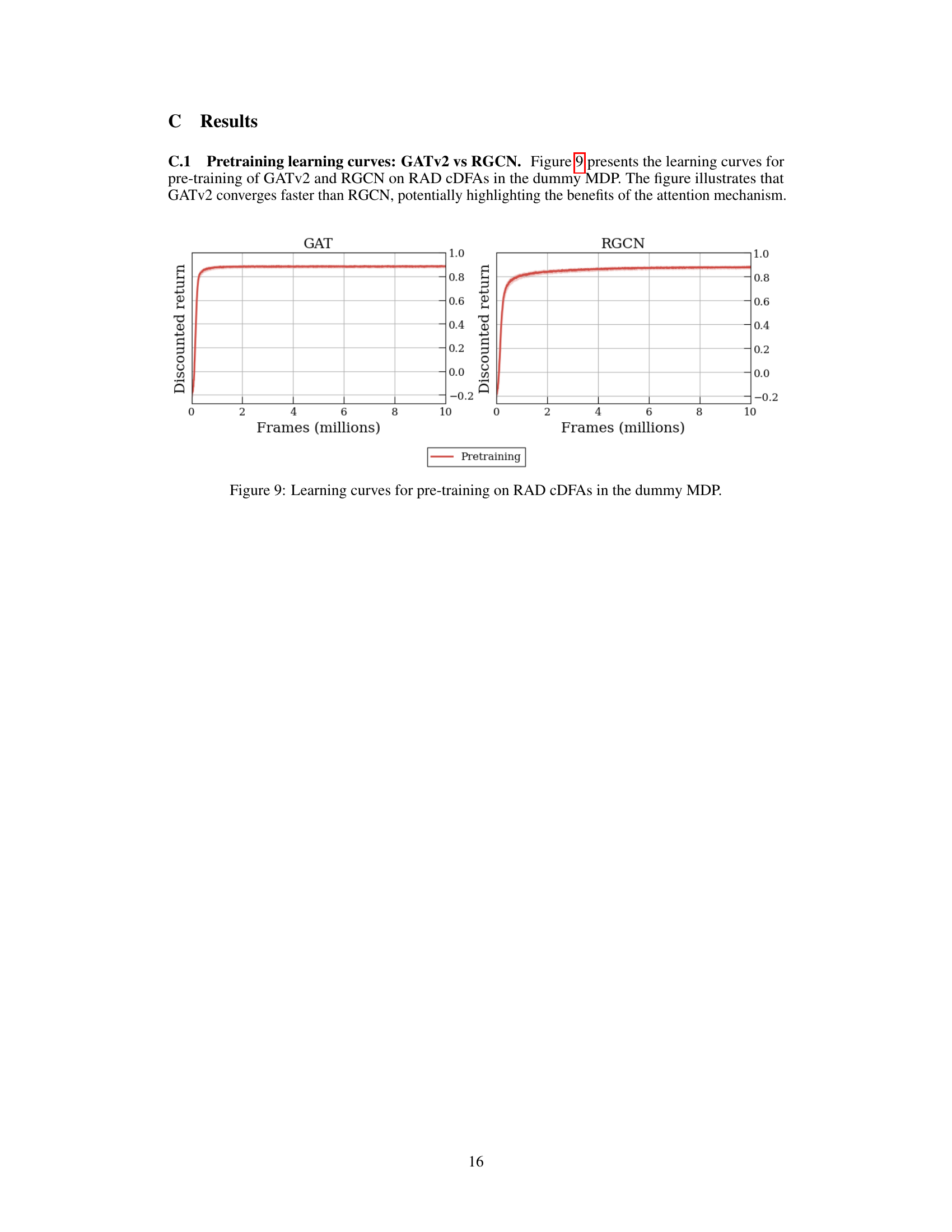
🔼 This figure shows the learning curves for pre-training the Graph Attention Network (GATv2) and Relational Graph Convolutional Network (RGCN) on Reach-Avoid Derived (RAD) Compositional Deterministic Finite Automata (cDFAs) within a dummy Markov Decision Process (MDP). The x-axis represents training frames (in millions), and the y-axis represents the discounted return. The curves illustrate the training progress of the two different network architectures on the RAD cDFA encoding task, highlighting the faster convergence of GATv2 compared to RGCN. This showcases the benefit of the attention mechanism in GATv2 for learning efficient cDFA embeddings.
read the caption
Figure 9: Learning curves for pre-training on RAD CDFAs in the dummy MDP.
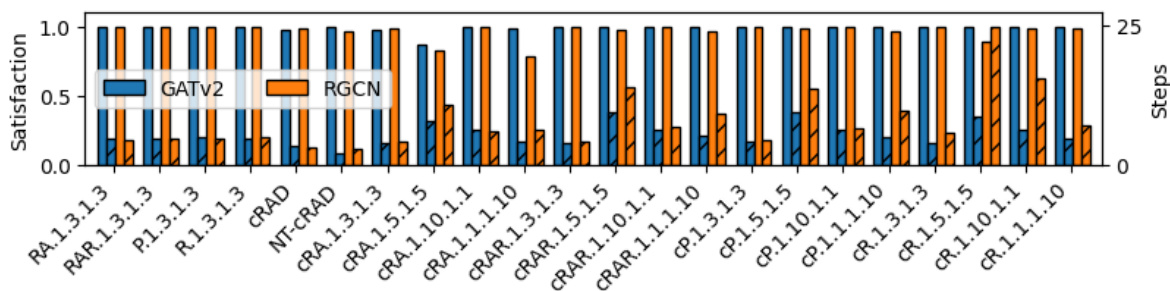
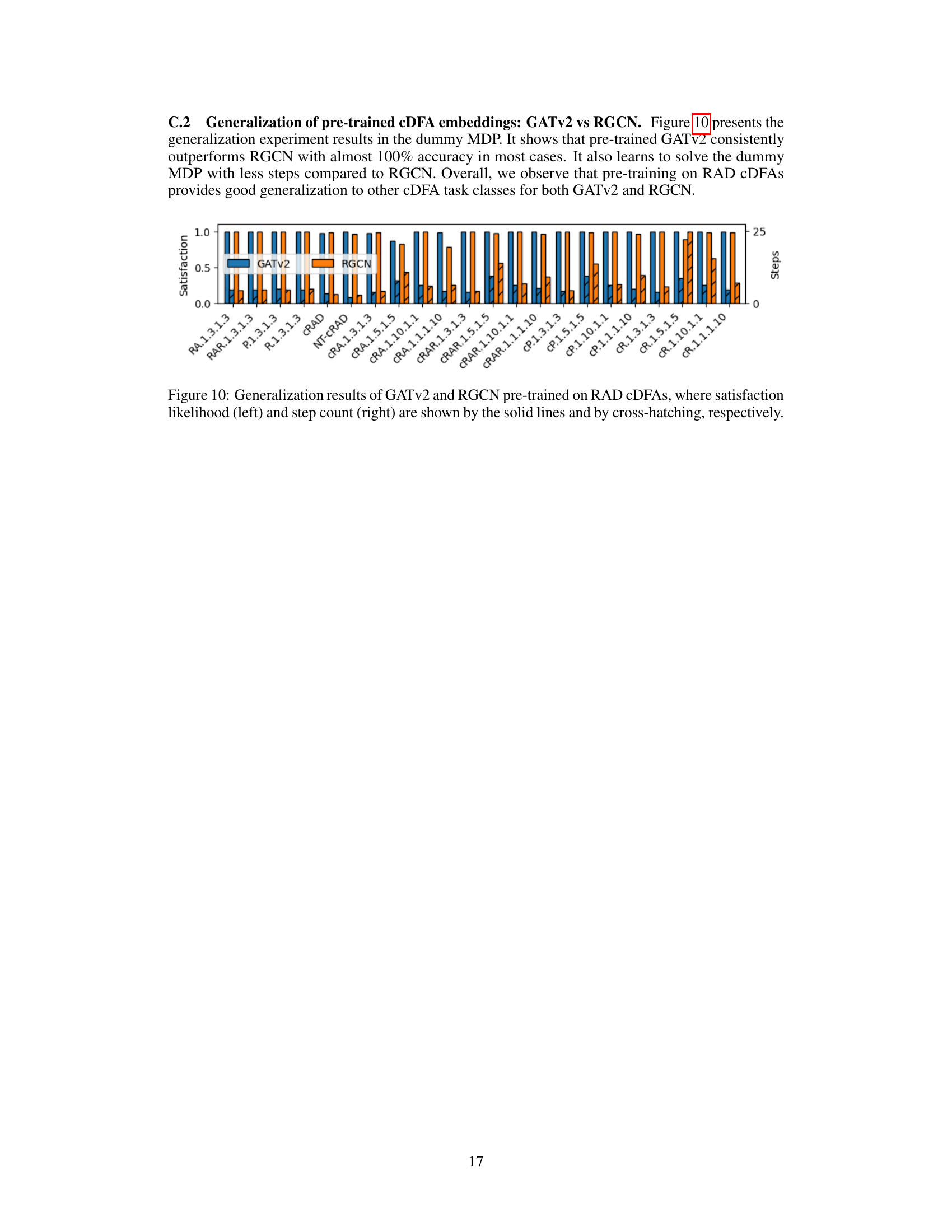
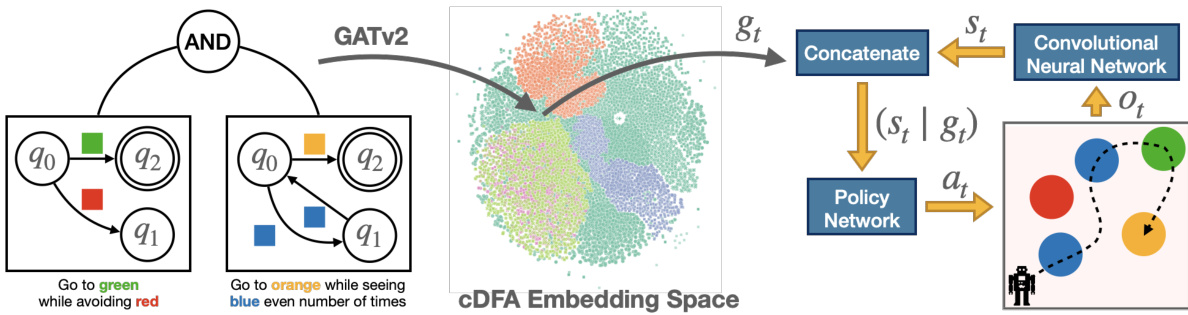
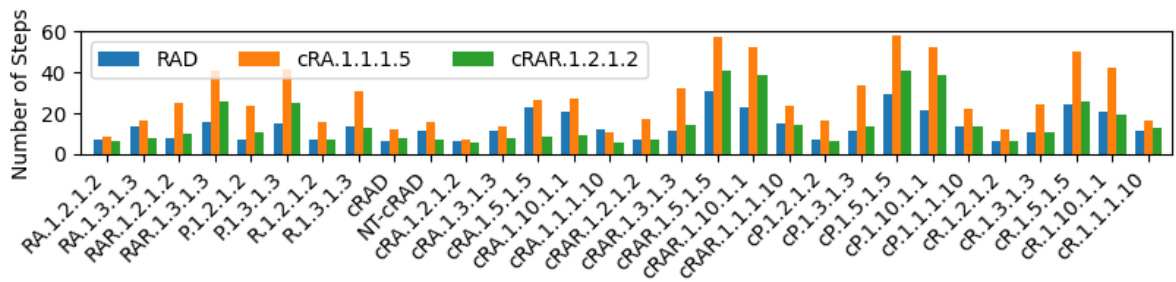
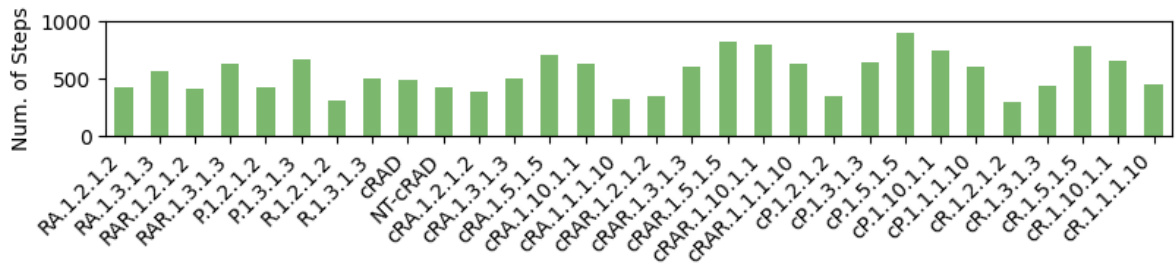
🔼 This figure presents the generalization results of GATv2 and RGCN models pre-trained on Reach-Avoid Derived (RAD) Compositional Deterministic Finite Automata (cDFAs) when tested on various unseen cDFA tasks. The left side shows the satisfaction likelihood (the probability of successfully completing the task), while the right shows the number of steps taken to complete the task. The results demonstrate that both GATv2 and RGCN generalize well to different cDFA task classes, though GATv2 consistently outperforms RGCN in most instances.
read the caption
Figure 10: Generalization results of GATv2 and RGCN pre-trained on RAD CDFAs, where satisfaction likelihood (left) and step count (right) are shown by the solid lines and by cross-hatching, respectively.

🔼 This figure illustrates the overall architecture of the proposed approach. A composition of deterministic finite automata (cDFA) represents the temporal goal. Each DFA within the composition is individually processed by a graph neural network (GATv2) which produces an embedding for that DFA. These individual DFA embeddings are then combined (using concatenation in this example) to create a single embedding representing the whole cDFA goal. This goal embedding is then used as input to a reinforcement learning policy network which determines the actions of the agent.
read the caption
Figure 1: Given a (conjunctive) composition of deterministic finite automata (shown on the left), we construct its embedding using a graph neural network (GATv2) and use this embedding as a goal to condition the reinforcement learning policy.
🔼 This figure illustrates the message passing mechanism used in the graph attention network (GATv2) to generate embeddings for compositional deterministic finite automata (cDFAs). It shows how the network processes the nodes and edges of the cDFA graph to create a vector representation that captures the temporal logic encoded within the cDFA. This embedding is then used as an input to the reinforcement learning policy network.
read the caption
Figure 2: Message passing illustration on the featurization of the cDFA given in Figure 1.
🔼 This figure illustrates the message passing mechanism used in the proposed architecture for featurizing compositional deterministic finite automata (cDFAs). It shows how the graph neural network (GATv2) processes the nodes and edges of a cDFA to generate an embedding representing the temporal task. The figure highlights the steps involved in creating the featurization, including adding new nodes for every transition, reversing edges, adding self-loops, and adding connections from initial states to a central ‘AND’ node. The message passing process is then visualized, showing how information is propagated through the network to produce the final cDFA embedding.
read the caption
Figure 2: Message passing illustration on the featurization of the cDFA given in Figure 1.
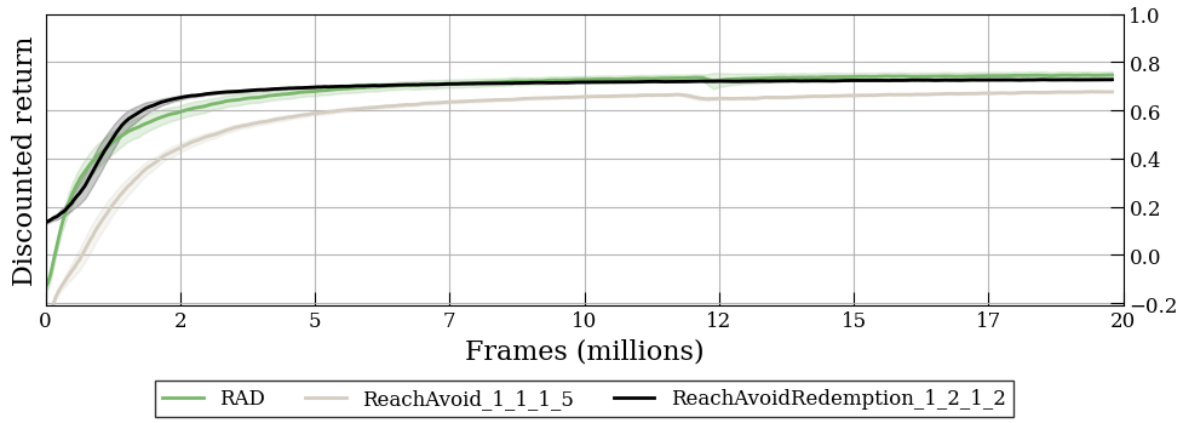
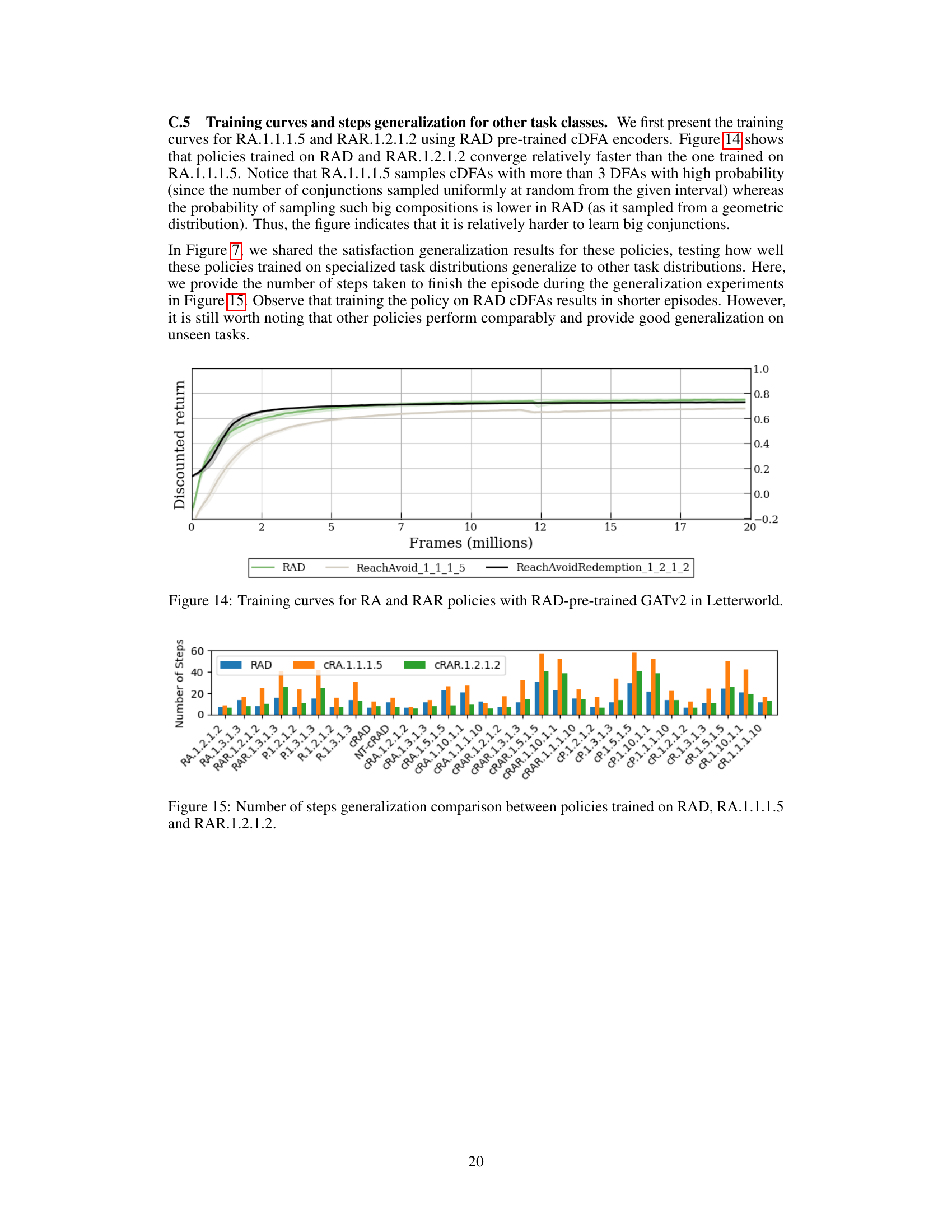
🔼 This figure shows the training curves for three different types of policies in the Letterworld environment: RAD, ReachAvoid_1_1_1_5, and ReachAvoidRedemption_1_2_1_2. The x-axis represents the number of frames (training steps), and the y-axis represents the discounted return, a measure of the policy’s performance. The curves show how the average discounted return changes over the course of training for each policy. The purpose is to demonstrate the impact of pre-training the graph attention network (GATv2) model on the RAD dataset on the learning curves of different policy types. The plot visually illustrates the relative convergence speed and performance levels achieved by these different policy approaches in this specific reinforcement learning task.
read the caption
Figure 14: Training curves for RA and RAR policies with RAD-pre-trained GATv2 in Letterworld.
🔼 This figure illustrates the message passing mechanism used in the graph attention network (GATv2) to generate an embedding for a compositional deterministic finite automaton (cDFA). The cDFA, representing a complex temporal task, is first featurized into a graph structure. The nodes of this graph represent states and transitions within the cDFA, with edge features encoding the symbols triggering those transitions. The GATv2 then performs a series of message-passing steps, where each node updates its feature vector based on information from its neighbors. This iterative process allows the network to capture the structure and semantics of the cDFA, finally culminating in a single vector embedding that represents the entire cDFA.
read the caption
Figure 2: Message passing illustration on the featurization of the cDFA given in Figure 1.

🔼 This figure illustrates the architecture for goal-conditioned reinforcement learning using compositional deterministic finite automata (cDFAs). A cDFA is represented as a composition of several DFAs which are shown on the left. The cDFA is passed to a graph attention network (GATv2), which creates an embedding of the cDFA. This embedding then serves as a goal to condition the reinforcement learning (RL) policy network on the right. The architecture incorporates an AND operation to combine the individual DFAs, a convolutional neural network (CNN) to encode observations, and a policy network to output actions. This design addresses the challenge of representing and using temporal goals in RL effectively.
read the caption
Figure 1: Given a (conjunctive) composition of deterministic finite automata (shown on the left), we construct its embedding using a graph neural network (GATv2) and use this embedding as a goal to condition the reinforcement learning policy.

🔼 This figure illustrates the message passing mechanism used in the graph attention network (GATv2) to generate embeddings for compositional deterministic finite automata (cDFAs). It shows how node features are updated through message passing steps, involving attention scores and linear transformations. The process transforms the cDFA graph structure into a vector representation that captures its essential properties for use in reinforcement learning.
read the caption
Figure 2: Message passing illustration on the featurization of the cDFA given in Figure 1.
🔼 This figure illustrates the message-passing mechanism used in the proposed architecture to featurize a compositional DFA (cDFA). It shows how a graph neural network processes the cDFA’s structure to generate an embedding that captures the temporal logic of the task. The process involves adding new nodes for transitions, reversing edges, adding self-loops, and connecting initial states to an ‘AND’ node to represent the conjunctive nature of the cDFA. The resulting embedding is then used as input to a policy network in a reinforcement learning setting.
read the caption
Figure 2: Message passing illustration on the featurization of the cDFA given in Figure 1.
🔼 This figure illustrates the message passing mechanism used in the graph attention network (GATv2) to generate an embedding for a compositional deterministic finite automaton (cDFA). The cDFA, representing a temporal task, is first featurized into a graph structure. The message passing process iteratively updates node features by aggregating information from neighboring nodes, weighted by attention scores. The final embedding of the cDFA is obtained from the ‘AND’ node, which aggregates information from all constituent DFAs. This embedding then serves as a goal representation for the reinforcement learning policy.
read the caption
Figure 2: Message passing illustration on the featurization of the cDFA given in Figure 1.
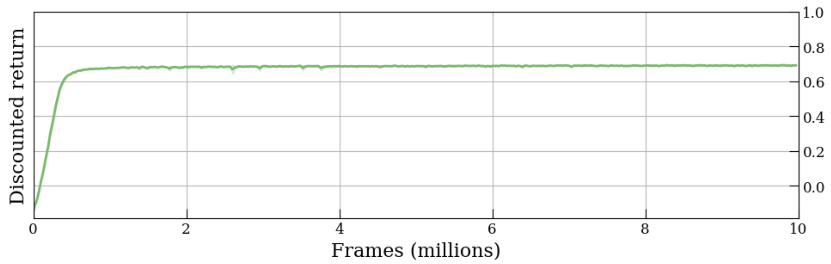
🔼 This figure shows the learning curves obtained during the pre-training phase of the experiment. Two different models, GATv2 and RGCN, are compared in terms of their performance on learning to encode RAD cDFAs. The x-axis represents the number of frames (millions) during training, while the y-axis displays the discounted return achieved by each model. The figure visually demonstrates that GATv2 converges faster than RGCN on this pre-training task.
read the caption
Figure 9: Learning curves for pre-training on RAD cDFAs in the dummy MDP.
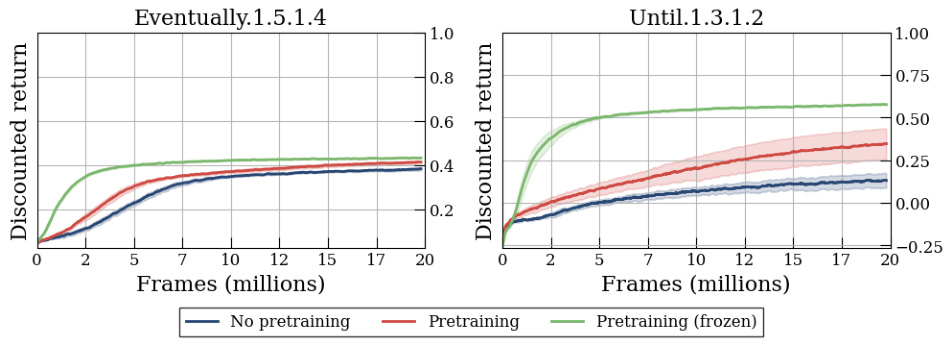
🔼 This figure shows the training curves for two different reinforcement learning environments, Letterworld (discrete states and actions) and Zones (continuous states and actions). The curves compare the performance of policies trained using three different methods: no pre-training, pre-training with a frozen encoder, and pre-training with an unfrozen encoder. The results indicate that pre-training significantly improves the learning process, and that freezing the encoder after pre-training yields even better results. The error bars represent the 90% confidence interval across 10 different training runs, showing the stability and consistency of the results.
read the caption
Figure 5: Training curves (error bars show a 90% confidence interval over 10 seeds) in Letterworld (discrete) and Zones (continuous) for policies trained on RAD CDFAs, showing that frozen pre-trained CDFA encoders perform better than non-frozen ones while no pre-training barely learns the tasks.

🔼 This figure illustrates the message-passing mechanism used in the proposed architecture for featurizing compositional deterministic finite automata (cDFAs). The architecture uses a graph attention network (GATv2) to encode cDFAs for use in goal-conditioned reinforcement learning. The figure shows how the nodes (states and transitions) of individual DFAs and their conjunctions are represented as a graph, and then how the message-passing steps are used to compute a vector embedding that represents the cDFA as a whole. The process involves multiple steps of message passing between nodes, updating node features at each step.
read the caption
Figure 2: Message passing illustration on the featurization of the cDFA given in Figure 1.
Full paper#