TL;DR#
Many real-world decision-making problems require maximizing return on investment (ROI), which is challenging because it involves optimizing the ratio between long-term return and cost. Existing reinforcement learning methods usually focus on maximizing return, while ignoring the cost. This can lead to inefficient policies that achieve high returns but with very high costs.
This research proposes a new framework and algorithm called ROIDICE to address this issue. ROIDICE uses a technique called linear fractional programming to directly optimize ROI and incorporates a method to handle the distribution shift inherent in offline learning. Experimental results on various tasks demonstrate that ROIDICE achieves a superior trade-off between return and cost compared to existing algorithms.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles the challenging problem of ROI maximization in offline reinforcement learning, a crucial area with broad applications. It offers a novel framework and algorithm (ROIDICE) that significantly improves policy efficiency by explicitly considering the trade-off between return and cost, addressing limitations of existing methods. This work opens avenues for more efficient decision-making in various domains and inspires further research into offline RL optimization with cost constraints.
Visual Insights#
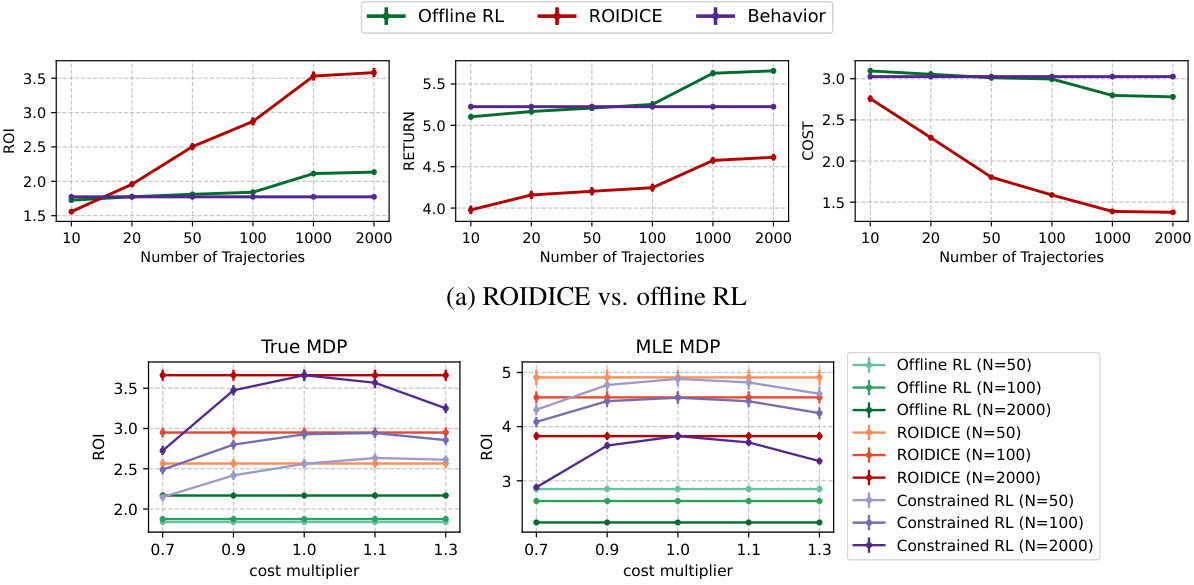
🔼 This figure compares the performance of ROIDICE against other offline reinforcement learning algorithms (offline RL and offline constrained RL). It shows the trade-off between return and accumulated cost for different numbers of trajectories in the training dataset. Subfigure (a) contrasts ROIDICE with a standard offline RL approach, highlighting ROIDICE’s superior efficiency in balancing return and cost. Subfigure (b) compares ROIDICE with an offline constrained RL method, demonstrating ROIDICE’s ability to achieve higher ROI even with cost constraints, particularly when the number of trajectories is sufficient.
read the caption
Figure 1: Comparison of ROIDICE with other offline algorithms. We average the scores and obtain ±2× standard error using 1000 seeds. N denotes the number of trajectories within the dataset.
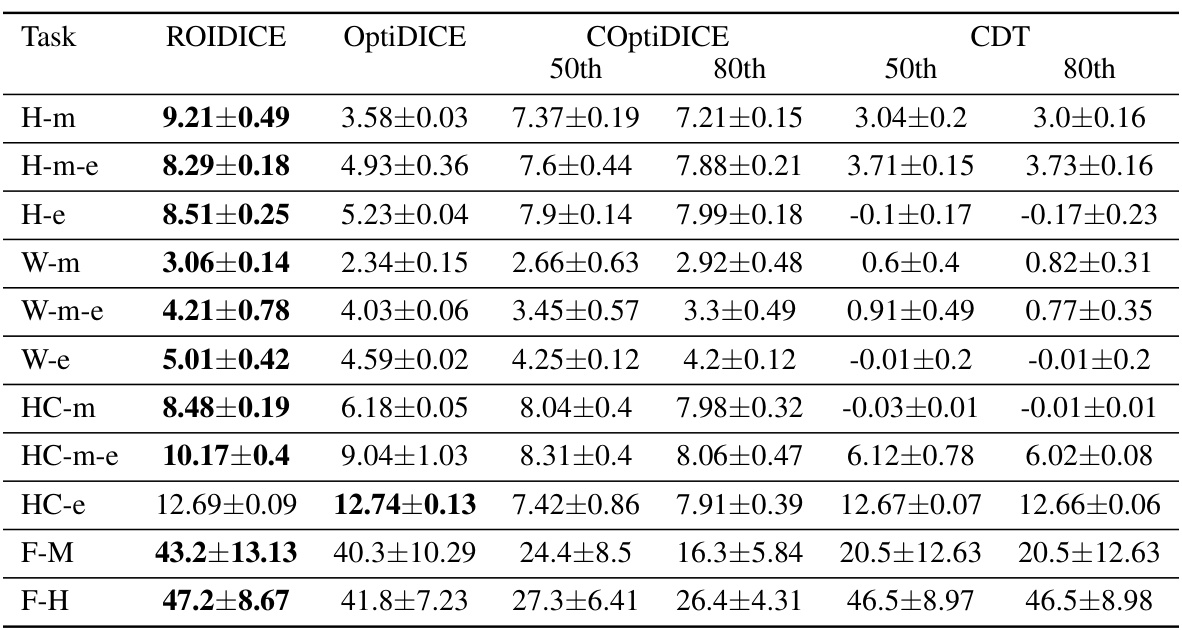
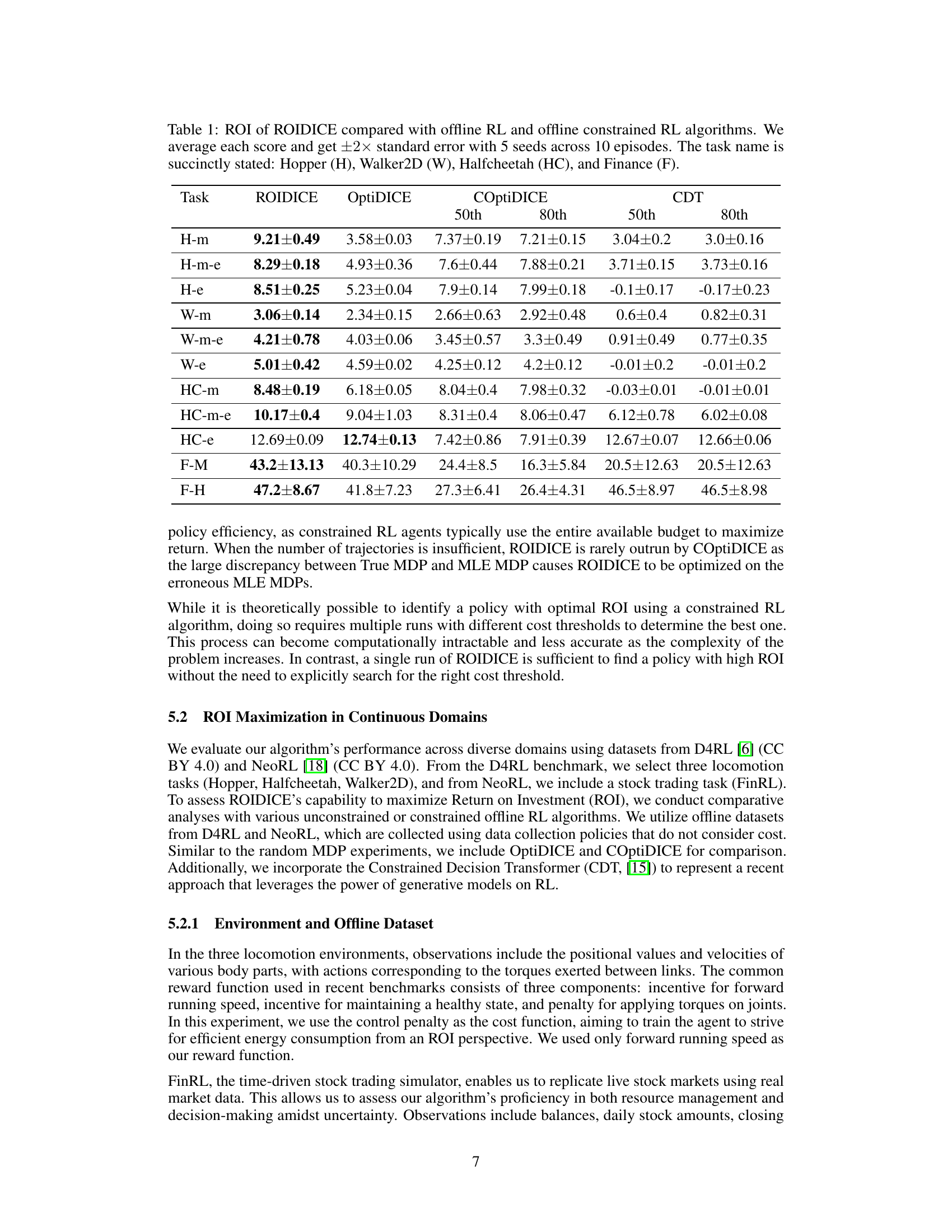
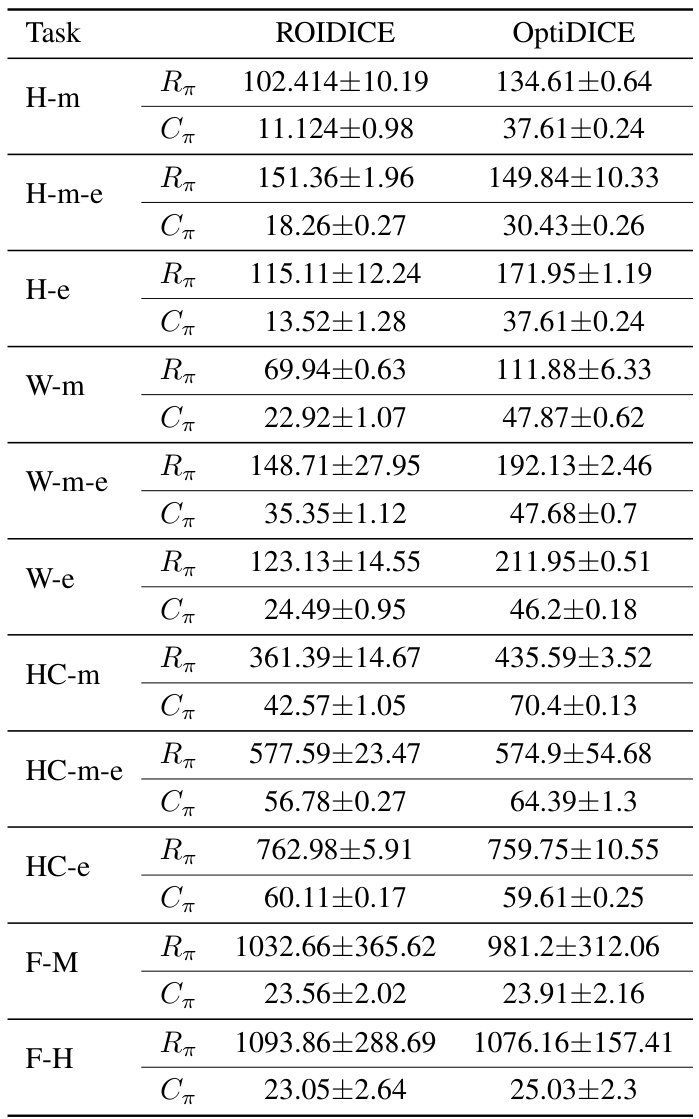
🔼 This table presents a comparison of the Return on Investment (ROI) achieved by the ROIDICE algorithm against other offline reinforcement learning methods, namely OptiDICE (offline RL) and COptiDICE (offline constrained RL), across various tasks. The tasks include locomotion tasks (Hopper, Walker2D, HalfCheetah) and a financial task (Finance). The results show the average ROI and standard error for each algorithm, providing a quantitative comparison of their performance in terms of efficiency (return relative to cost).
read the caption
Table 1: ROI of ROIDICE compared with offline RL and offline constrained RL algorithms. We average each score and get ±2× standard error with 5 seeds across 10 episodes. The task name is succinctly stated: Hopper (H), Walker2D (W), Halfcheetah (HC), and Finance (F).
In-depth insights#
Offline ROI Maximization#
Offline ROI maximization presents a unique challenge in reinforcement learning, demanding efficient policy optimization with limited data. The core problem lies in balancing exploration and exploitation with a fixed dataset, making it hard to improve a policy’s return without risking a significant increase in cost. Approaches like formulating ROI as a linear fractional program and using techniques such as stationary distribution correction (DICE) show promise. Algorithms like ROIDICE cleverly address the inherent distribution shift in offline RL by leveraging stationary distributions and incorporating convex regularization. This dual focus on return and cost yields a superior tradeoff compared to traditional methods that optimize for return alone, resulting in more efficient and practical policies. However, the success of such methods is sensitive to the quality of the offline dataset and the design of the cost function; inaccurate or poorly designed cost structures might skew the results.
ROIDICE Algorithm#
The ROIDICE algorithm is a novel offline reinforcement learning method designed to maximize Return on Investment (ROI) in Markov Decision Processes. Its key innovation lies in formulating the ROI maximization problem as a linear fractional program, which efficiently handles the ratio of long-term return and cost. Unlike standard reinforcement learning, which primarily focuses on maximizing cumulative rewards, ROIDICE explicitly balances reward and cost. ROIDICE incorporates stationary distribution correction (DICE) to address the challenges of offline learning, mitigating distribution shift and enhancing the algorithm’s practicality. By leveraging the dual formulation of value-iteration linear programming, ROIDICE offers a principled approach for optimizing efficiency. The algorithm’s effectiveness is demonstrated through experiments showcasing superior ROI and cost-efficiency compared to existing offline RL algorithms, providing a promising solution for real-world scenarios where resource management is critical.
Linear Fractional Prog#
Linear fractional programming (LFP) presents a powerful yet often overlooked technique for optimization problems involving the ratio of two linear functions. Its strength lies in directly addressing objectives framed as ratios, such as Return on Investment (ROI), rather than resorting to approximations or transformations. The ROI maximization problem, a key focus in the paper, is naturally suited to LFP because ROI itself is defined as a ratio of returns over costs. The Charnes-Cooper transformation is a crucial aspect, allowing conversion of the LFP problem into a standard linear program (LP). This transformation makes the problem readily solvable using existing LP techniques and algorithms. However, the paper also highlights challenges inherent in applying LFP to sequential decision-making scenarios in a Markov Decision Process (MDP). The offline setting further complicates things, adding distribution shift issues that need specific handling. The paper directly tackles these challenges to effectively leverage LFP for efficient decision making. By converting ROI maximization to LFP, the researchers create a framework that’s both mathematically elegant and practically applicable, yielding an algorithm tailored to offline policy optimization with a strong ROI focus.
Empirical Evaluation#
A robust empirical evaluation section should present a multifaceted assessment of the proposed method. It needs to clearly define the experimental setup, including datasets used, metrics employed, and baselines considered for comparison. Comprehensive quantitative results, ideally visualized with clear graphs and tables, are crucial for demonstrating the effectiveness of the proposed approach. Statistical significance tests should be included to support claims of improvement, and the results should be discussed in detail. Ablation studies are vital for analyzing the contribution of each component of the method. Error analysis can provide additional insight into scenarios where the method might fail or underperform. Finally, a discussion of the results’ implications, potential limitations, and directions for future work should conclude this section. Reproducibility should be emphasized, with sufficient details provided for others to replicate the experiments.
Future Work#
Future work could explore extending ROIDICE to handle continuous state and action spaces, improving its scalability for real-world applications. Addressing the challenge of distribution shift in offline RL more effectively is crucial, perhaps through more advanced techniques beyond the convex regularization currently employed. Investigating the impact of different cost functions and their influence on policy efficiency would provide valuable insights into the algorithm’s robustness and applicability across diverse domains. Additionally, a comparative analysis against other offline RL methods that directly optimize for Pareto efficiency would offer a more nuanced understanding of ROIDICE’s strengths and limitations. Finally, applying ROIDICE to diverse real-world problems, such as resource management in robotics or personalized medicine, will demonstrate its practical impact and identify areas for further improvement.
More visual insights#
More on figures
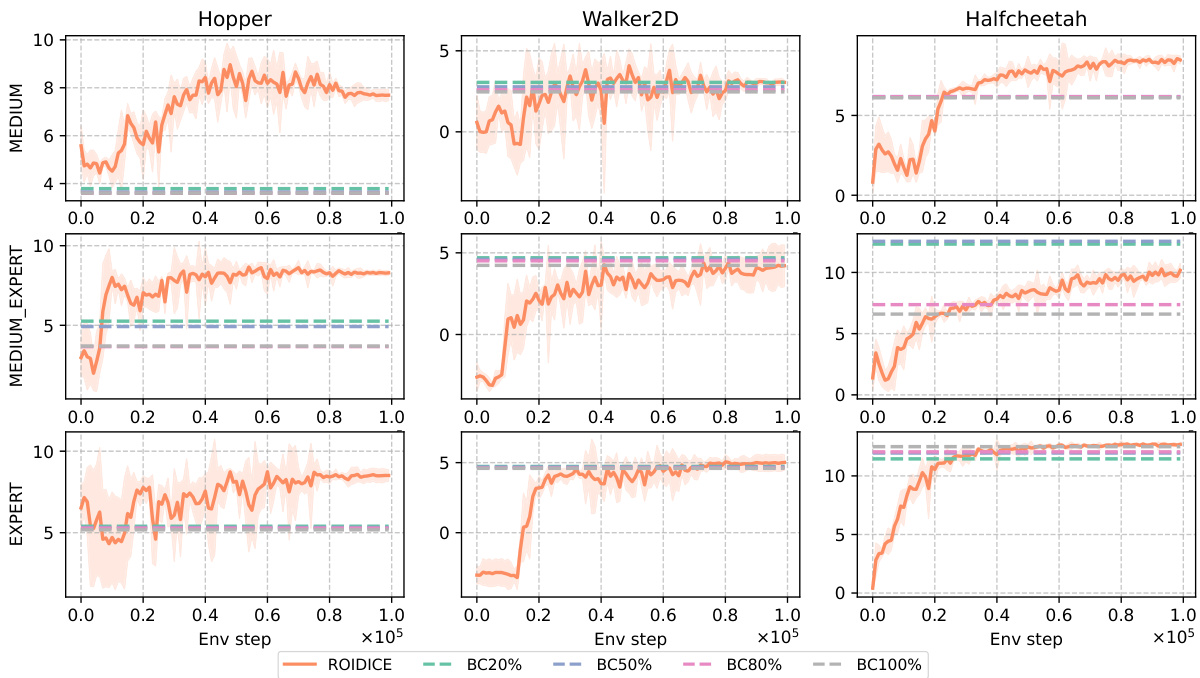
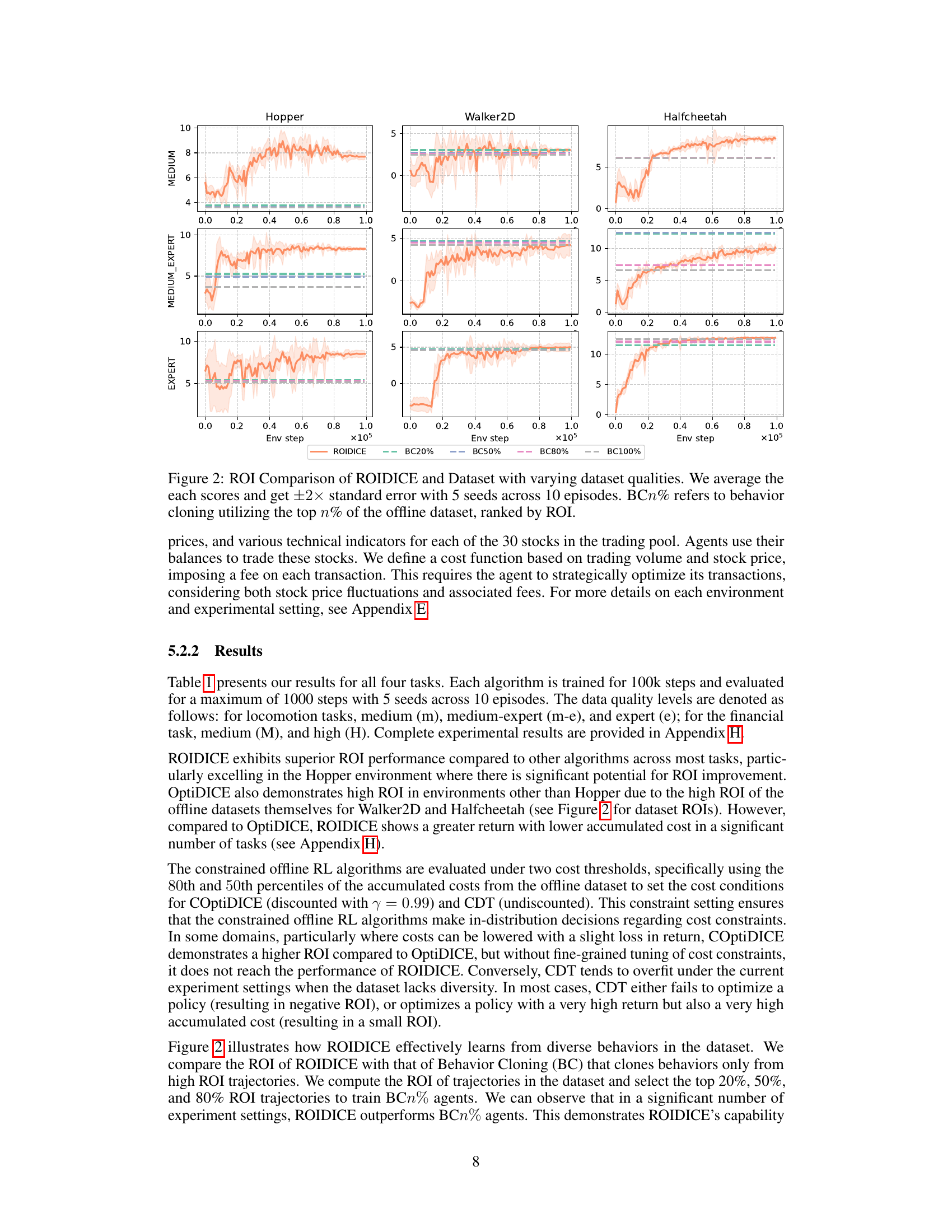
🔼 This figure compares the Return on Investment (ROI) performance of ROIDICE against behavior cloning (BC) using different percentages of the dataset. The dataset is ranked by ROI, and BC20%, BC50%, BC80%, and BC100% represent using the top 20%, 50%, 80%, and 100% of the dataset respectively. The results show how ROIDICE’s performance compares to simply cloning the best performing policies from the dataset, illustrating its ability to learn from a diverse set of experiences.
read the caption
Figure 2: ROI Comparison of ROIDICE and Dataset with varying dataset qualities. We average the each scores and get ±2× standard error with 5 seeds across 10 episodes. BCn% refers to behavior cloning utilizing the top n% of the offline dataset, ranked by ROI.
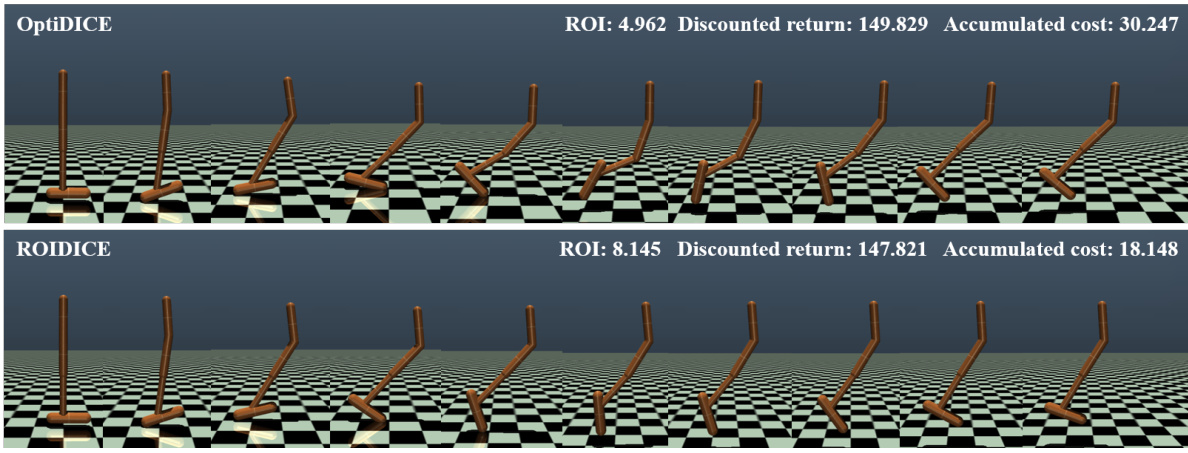
🔼 This figure compares the qualitative behavior of ROIDICE and OptiDICE in the Hopper environment. It shows a sequence of states/actions taken by both agents. The visual comparison highlights how ROIDICE, by optimizing for ROI, achieves a higher return with a lower accumulated cost compared to OptiDICE, which focuses solely on maximizing return. The difference can be seen in the smoother, more efficient movements produced by ROIDICE in contrast to the less efficient jumps by OptiDICE.
read the caption
Figure 3: Visualization of ROIDICE and OptiDICE in Hopper environment.
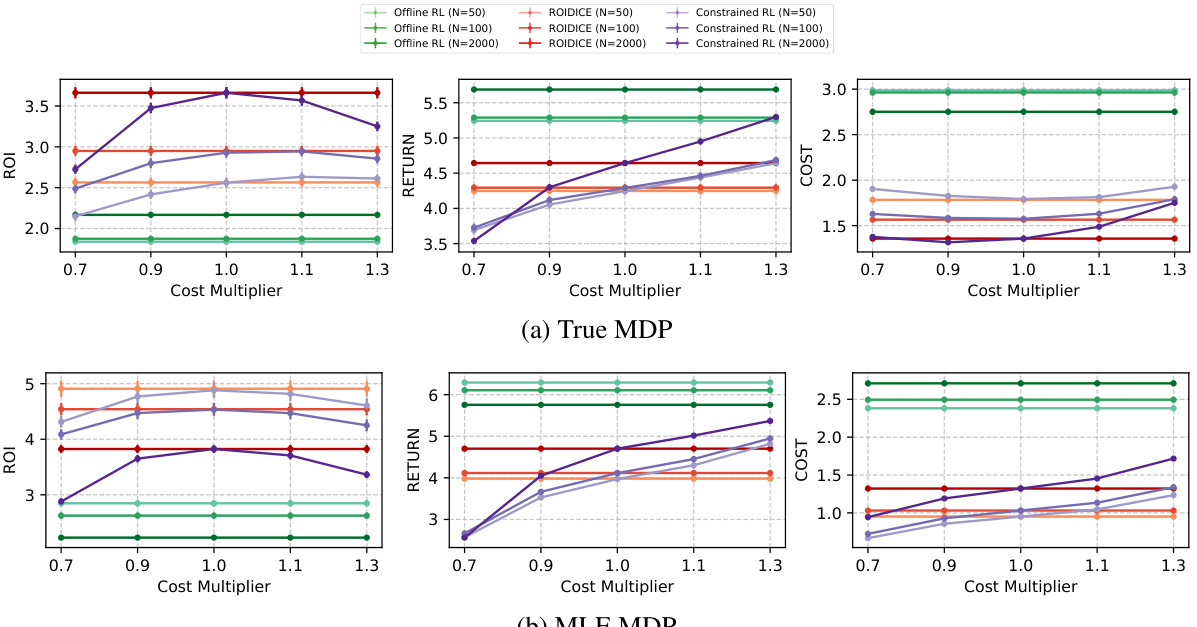
🔼 The figure compares ROIDICE’s performance against other offline algorithms (offline RL and offline constrained RL) across different numbers of trajectories (dataset sizes). Subfigure (a) contrasts ROIDICE with offline RL, showing that ROIDICE achieves higher ROI (return on investment) by balancing return and cost more effectively than offline RL which prioritizes maximizing return. Subfigure (b) compares ROIDICE against offline constrained RL algorithms. While constrained RL aims to maximize return subject to a cost constraint, ROIDICE consistently achieves higher ROI than constrained RL across various cost constraint thresholds, particularly with larger datasets. This highlights ROIDICE’s unique ability to optimize for a superior trade-off between return and cost, leading to improved policy efficiency.
read the caption
Figure 1: Comparison of ROIDICE with other offline algorithms. We average the scores and obtain ±2× standard error using 1000 seeds. N denotes the number of trajectories within the dataset.

🔼 This figure shows the effect of different values of the hyperparameter α on the performance of the ROIDICE algorithm across three locomotion tasks (Hopper, Walker2D, and Halfcheetah) using expert-level datasets. The hyperparameter α controls the strength of the regularization in ROIDICE, balancing between return maximization and distribution shift. The plot displays the average ROI achieved with varying values of α, along with error bars representing the standard error across 5 seeds and 10 episodes. By examining how ROI changes with α, we can understand the trade-off between regularization and maximizing return in the algorithm.
read the caption
Figure 5: Comparison of different levels of the hyperparameter (α) of ROIDICE in locomotion environments using expert data quality. We average the scores and obtain ±2× standard error using 5 seeds across 10 episodes.

🔼 This figure compares the performance of ROIDICE against other offline RL algorithms (OptiDICE) and offline constrained RL algorithms (COptiDICE) across different numbers of trajectories in the dataset. Subfigure (a) shows ROIDICE achieving a superior trade-off between return and cost compared to OptiDICE, which prioritizes maximizing return. Subfigure (b) demonstrates that ROIDICE outperforms COptiDICE, which maximizes return under a cost constraint, particularly when the cost threshold is set appropriately. The results highlight ROIDICE’s effectiveness in optimizing ROI by efficiently balancing return and cost.
read the caption
Figure 1: Comparison of ROIDICE with other offline algorithms. We average the scores and obtain ±2× standard error using 1000 seeds. N denotes the number of trajectories within the dataset.
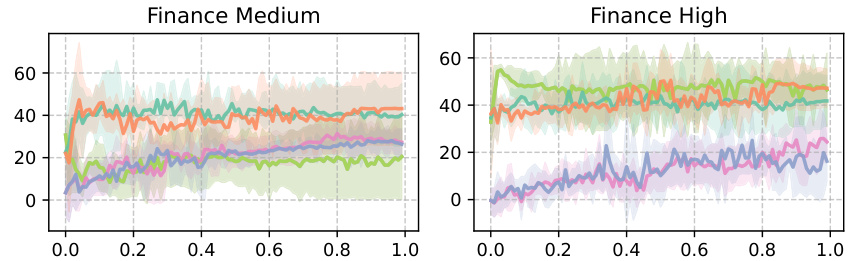
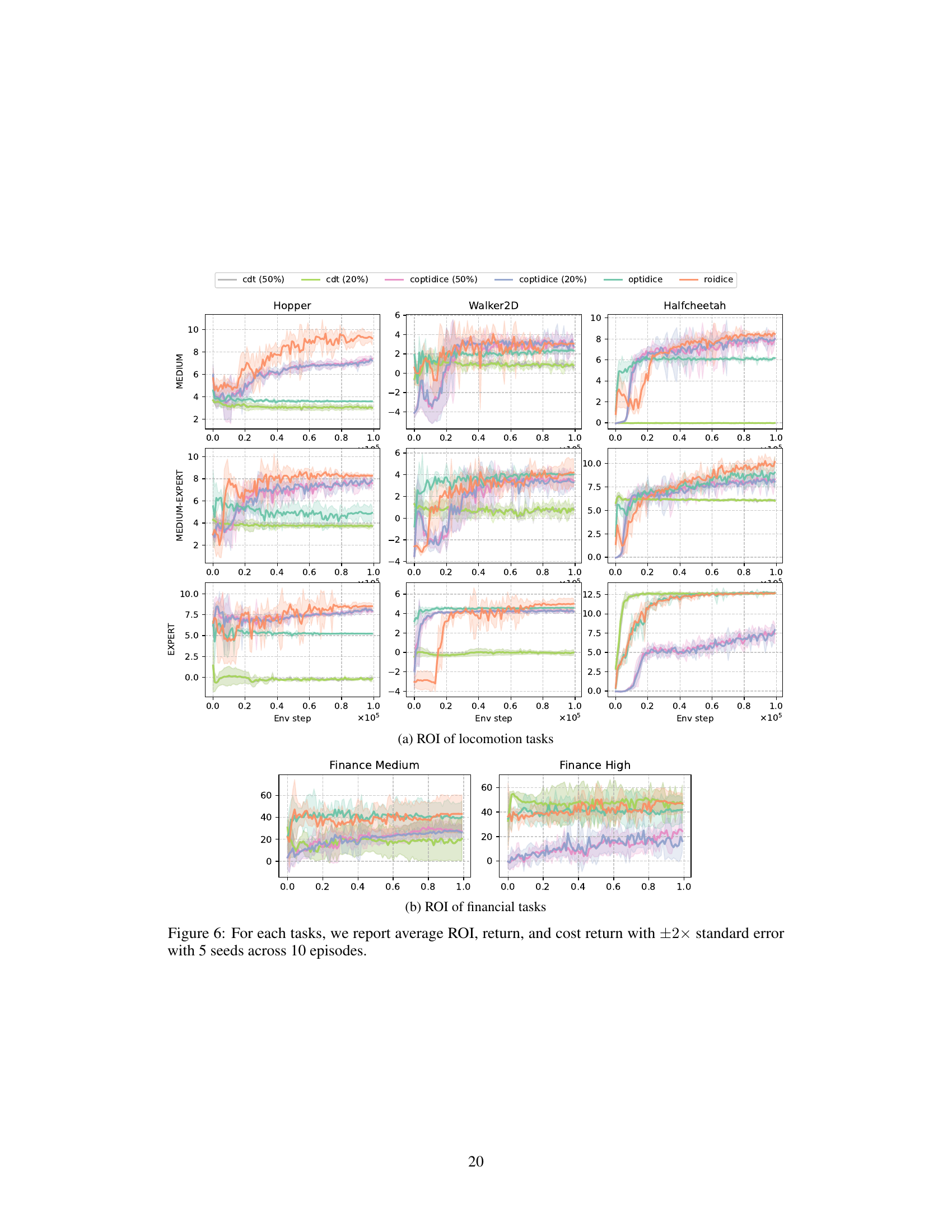
🔼 This figure compares the performance of ROIDICE, OptiDICE, COptiDICE, and CDT across different tasks (locomotion and finance) and dataset qualities (medium and high). For each task and dataset, the figure shows the average ROI, return, and cost return over 10 episodes, with error bars representing the standard error across 5 seeds. This allows for a visual comparison of the different algorithms’ performance in terms of efficiency (ROI), reward, and cost.
read the caption
Figure 6: For each tasks, we report average ROI, return, and cost return with ±2× standard error with 5 seeds across 10 episodes.
More on tables

🔼 This table lists the hyperparameters used in the reward and cost functions for the financial task in the FinRL environment. It shows the values assigned to parameters
w<sup>m</sup><sub>c</sub>,b<sup>m</sup><sub>c</sub>,w<sup>f</sup><sub>r</sub>,w<sup>f</sup><sub>c</sub>, andb<sup>f</sup><sub>c</sub>, which control aspects of the reward and cost calculations related to trading volume and stock prices.read the caption
Table 2: Reward and cost function hyperparameters
🔼 This table presents a comparison of the Return on Investment (ROI) achieved by the proposed ROIDICE algorithm against other offline reinforcement learning methods, including OptiDICE (offline RL) and COptiDICE (offline constrained RL) across various tasks. The results show the average ROI and the standard error across multiple trials (5 seeds and 10 episodes) for each algorithm on four different tasks: Hopper, Walker2D, Halfcheetah, and Finance. The task names are abbreviated for brevity.
read the caption
Table 1: ROI of ROIDICE compared with offline RL and offline constrained RL algorithms. We average each score and get ±2× standard error with 5 seeds across 10 episodes. The task name is succinctly stated: Hopper (H), Walker2D (W), Halfcheetah (HC), and Finance (F).

🔼 This table compares the computation time and the number of parameters of four algorithms: ROIDICE, OptiDICE, COptiDICE, and CDT. All algorithms were trained for 100,000 iterations using a single NVIDIA RTX 4090 GPU. The comparison highlights the computational efficiency differences between the algorithms, particularly noticeable in the training time for locomotion tasks versus finance tasks.
read the caption
Table 4: Comparison of the runtime and number of parameters between algorithms. All algorithms, including baseline methods, were trained for 100K iterations on a single NVIDIA RTX 4090 GPU.
🔼 This table presents a comparison of the performance of the ROIDICE algorithm against OptiDICE, an offline RL algorithm. For various tasks (including locomotion tasks like Hopper, Walker2D, HalfCheetah and financial tasks like F-M and F-H), the table shows the average return (Rπ), average accumulated cost (Cπ), and ROI achieved by both algorithms. The results illustrate the trade-off between return and cost achieved by each algorithm, highlighting ROIDICE’s focus on maximizing ROI (Return on Investment).
read the caption
Table 5: Results of ROIDICE compared with offline RL algorithms.

🔼 This table compares the performance of ROIDICE against other offline constrained reinforcement learning algorithms, namely COptiDICE and CDT, across various tasks and dataset qualities. The results show ROI (Return on Investment), return (Rπ), and cost (Cπ) for each algorithm and task, with error bars indicating the standard error across multiple trials. The table highlights the trade-off between return and accumulated cost, showcasing ROIDICE’s ability to achieve superior performance in several scenarios.
read the caption
Table 6: Results of offline constrained RL algorithms.

🔼 This table compares the Return on Investment (ROI) achieved by ROIDICE against three other offline constrained reinforcement learning algorithms (VOCE 50th, VOCE 80th, CPQ 50th, and CPQ 80th) across three different data quality levels (medium, medium-expert, and expert). The ROI is a measure of the efficiency of a policy, balancing return and accumulated cost. The results show ROIDICE consistently outperforms the other algorithms across all data quality levels, indicating its effectiveness in optimizing policy efficiency. The ‘50th’ and ‘80th’ suffixes denote the cost constraints used for the constrained algorithms, representing the 50th and 80th percentiles of accumulated cost in the offline dataset.
read the caption
Table 7: ROI of ROIDICE compared with offline constrained RL algorithms. We average each score and get ±2× standard error with 5 seeds across 10 episodes.

🔼 This table presents the Return on Investment (ROI) achieved by ROIDICE and COptiDICE on two safety-related tasks from the OpenAI SafetyGym environment: CarGoal and PointPush. The results are averaged over five different seeds, each run for ten episodes. The table shows that ROIDICE outperforms COptiDICE, suggesting that the proposed algorithm is more efficient in these safety-critical scenarios.
read the caption
Table 8: ROI of ROIDICE compared with offline constrained RL algorithms. We average each score and get ±2× standard error with 5 seeds across 10 episodes.
Full paper#