TL;DR#
Many real-world systems require the fair allocation of constrained resources where preferences are uncertain. Existing methods often struggle with fairness or scalability when faced with such uncertainty. This paper tackles the challenging problem of fair constrained resource allocation under uncertainty.
The researchers propose using robust optimization (minimizing the worst-case outcome) and Conditional Value at Risk (CVaR) optimization (maximizing expected welfare given a certain risk level) to address the uncertainty. They develop efficient algorithms for utilitarian and egalitarian welfare objectives, accounting for fairness both to individuals and groups. Experiments on reviewer assignment datasets demonstrate the effectiveness of their approaches.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in resource allocation, fairness, and optimization under uncertainty. It bridges the gap between theoretical advancements and practical applications, providing scalable and efficient algorithms adaptable to various real-world scenarios. The robust and CVaR approaches presented offer significant improvements over existing methods, opening avenues for further research into fairness-aware optimization techniques. The study’s emphasis on fairness is particularly timely and relevant, given the increasing demand for equitable resource distribution.
Visual Insights#

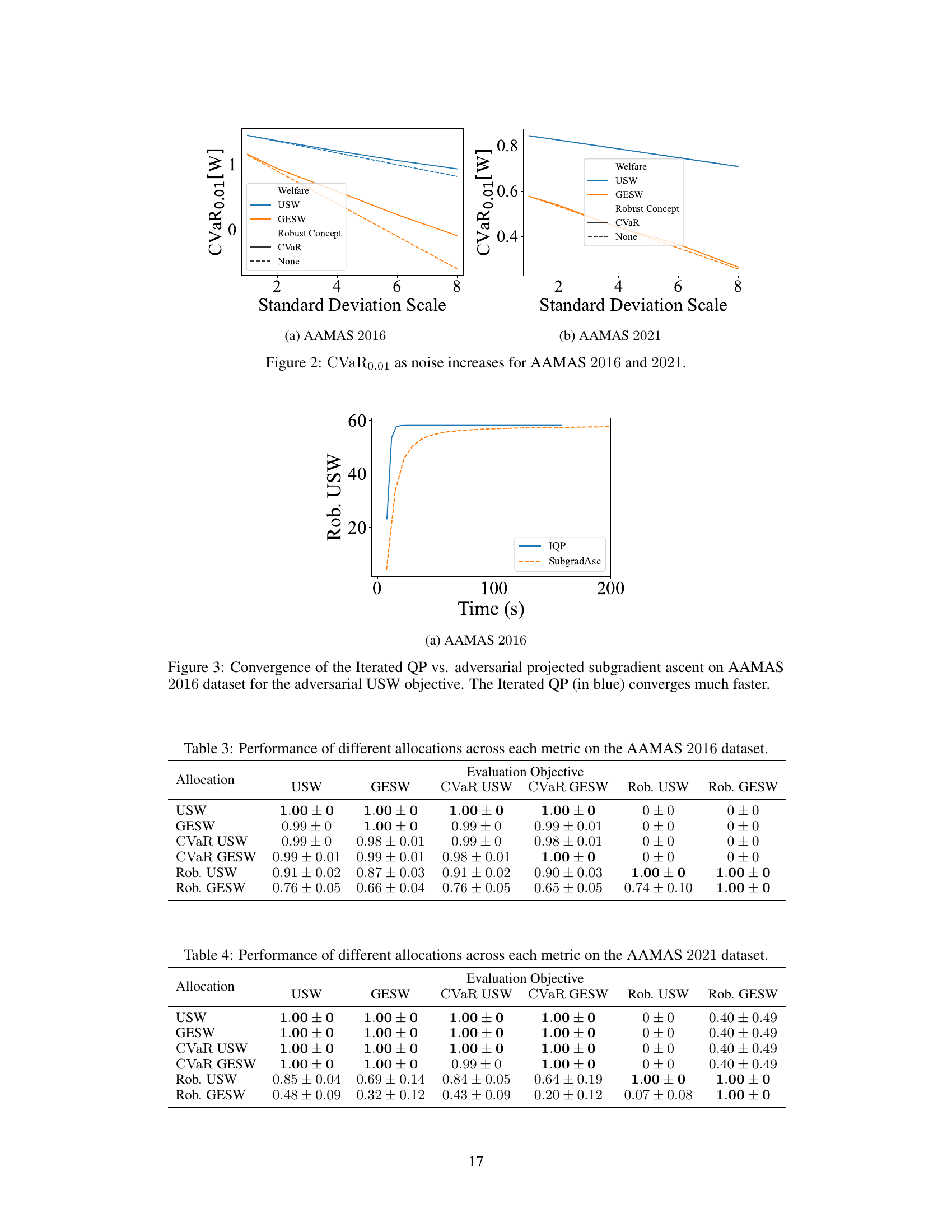
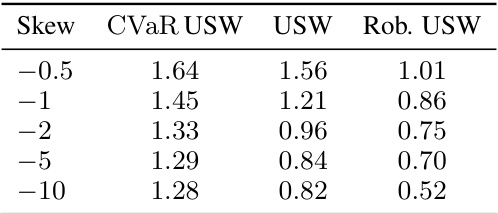
🔼 The left plot shows how CVaR of utilitarian social welfare (USW) and group egalitarian social welfare (GESW) change with increasing uncertainty (represented by standard deviation scale). The right plot compares the convergence speed of two optimization algorithms: Iterated Quadratic Programming and Adversarial Projected Subgradient Ascent, applied to the robust USW maximization problem.
read the caption
Figure 1: Left: CVaR as noise increases for AAMAS 2015. Right: Convergence behavior of the Iterated Quadratic Program (Iterated QP) vs. Adversarial Projected Subgradient Ascent approach on AAMAS 2015.
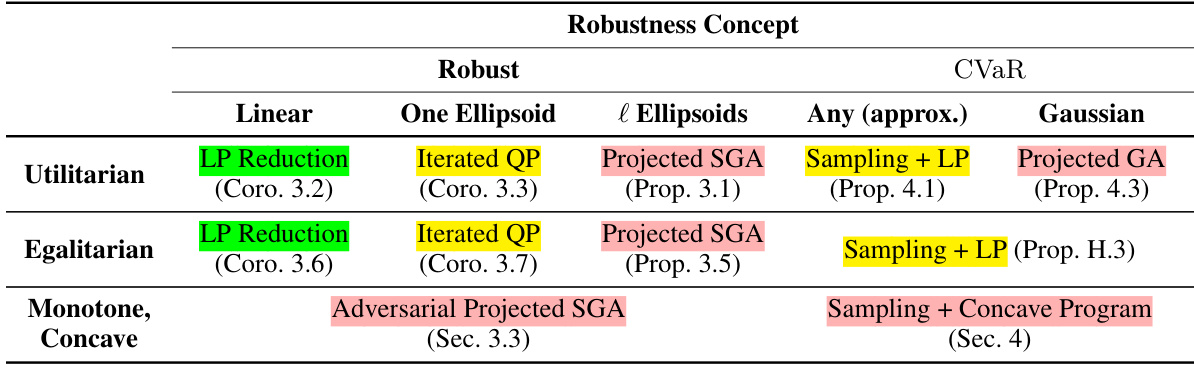
🔼 This table summarizes the computational complexity of different optimization algorithms used to solve for utilitarian and egalitarian welfare under different uncertainty models (robust and CVaR). It categorizes algorithms based on the type of uncertainty set and the welfare function used, indicating the complexity of each algorithm as low, medium, or high.
read the caption
Table 1: Summary of optimization algorithms for efficiently computing utilitarian and egalitarian welfare under different robustness concepts. Green highlights indicate problems which require solving a single linear program (low difficulty). Yellow highlights indicate solving a small number of linear or quadratic programs (medium difficulty). Red highlights indicate problems which require solving numerous quadratic programs or arbitrary concave programs.
In-depth insights#
Robust Welfare#
The concept of “Robust Welfare” in resource allocation problems, particularly under uncertainty, centers on optimizing welfare objectives while accounting for unpredictable variations in agent preferences or resource availability. This contrasts with traditional approaches that assume perfect knowledge of preferences. Robust methods aim to guarantee a minimum level of welfare even under the worst-case scenario within a defined uncertainty set, thereby providing greater resilience and fairness against unforeseen circumstances. Different paradigms exist for modeling uncertainty, such as stochastic optimization, which incorporates probabilistic information about possible preferences, and robust optimization, which focuses on the worst-case scenario within a given uncertainty set. The choice of paradigm affects the optimization algorithms employed and the resulting allocations. Furthermore, the chosen welfare objective (utilitarian or egalitarian) influences the optimization process and the ultimate fairness and efficiency of the resource allocation. Computational tractability is another crucial aspect, with robust optimization often posing significant computational challenges for complex problems. Efficient algorithms, such as those presented in the paper, are therefore essential to make robust welfare optimization viable in practice.
Uncertainty Sets#
The concept of ‘uncertainty sets’ is crucial for robust optimization, particularly when dealing with unknown or uncertain parameters in a resource allocation problem. These sets define a range of plausible values for the uncertain parameters, essentially representing the modeler’s belief about the level of uncertainty. The choice of uncertainty set significantly impacts the resulting solution’s robustness and computational tractability. Ambitious uncertainty sets may lead to overly conservative solutions, while overly restrictive ones may fail to capture important variations. Therefore, a careful balance needs to be struck between capturing enough uncertainty to ensure robustness and avoiding excessive conservatism. Furthermore, the shape of the uncertainty set, whether it’s polyhedral, ellipsoidal, or another form, affects the complexity of the optimization problem. Linearity, for instance, significantly simplifies the problem. The method for generating the uncertainty sets, whether using statistical techniques, expert judgment, or historical data, is also a critical factor, with various methods offering different trade-offs in accuracy and computational cost. The overall goal is to design uncertainty sets that faithfully reflect the true uncertainty while still allowing for efficient solution techniques.
CVaR Allocation#
The heading ‘CVaR Allocation’ suggests a methodology for resource allocation that incorporates risk aversion. CVaR (Conditional Value at Risk) is a measure of risk that focuses on the expected losses in the tail of the distribution, offering a more nuanced perspective than simply considering the average. This approach likely models the uncertainty inherent in predicting future utilities or values of resources, acknowledging that some outcomes are more costly than others. The authors likely leverage CVaR to optimize resource allocation for scenarios with uncertainty, prioritizing allocations that minimize the potential for significant negative outcomes, balancing overall welfare with risk management. This is particularly useful when dealing with limited resources and consequential outcomes, emphasizing a risk-averse optimization strategy that avoids potentially disastrous results. Therefore, ‘CVaR Allocation’ likely presents a robust and practical solution for resource allocation problems under uncertainty, especially for scenarios demanding high reliability and fairness.
Empirical Studies#
An Empirical Studies section in a research paper would ideally present a robust evaluation of the proposed methods. This would involve a detailed description of the datasets used, ensuring they are representative and publicly available. The choice of evaluation metrics is crucial, aligning with the paper’s objectives (e.g., fairness, efficiency, robustness). Results should be presented clearly, often with visualizations such as graphs, showing how the proposed methods perform against existing baselines across various settings and parameters. Statistical significance should be rigorously addressed, clarifying whether observed improvements are indeed meaningful. Furthermore, the computational efficiency and scalability of the methods must be discussed, comparing runtimes and resource requirements under different conditions. A discussion of the limitations of the experimental setup is vital, acknowledging any factors that might affect the generalizability or external validity of the results. Finally, an in-depth analysis interpreting the findings would be expected, relating the performance to the theoretical underpinnings and providing concrete implications of the study.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the robust optimization framework to handle more complex uncertainty sets beyond ellipsoidal and polyhedral forms is crucial for broader applicability. Investigating alternative fairness criteria, such as envy-freeness or proportionality, alongside the utilitarian and egalitarian objectives, would enrich the analysis and offer diverse allocation strategies. Developing more efficient algorithms for solving the robust and stochastic optimization problems, especially for large-scale datasets, is vital for practical implementation. Incorporating fairness constraints directly into the learning process for utility estimation could improve prediction accuracy and fairness simultaneously. Finally, empirical evaluations on diverse real-world applications (beyond reviewer assignment) will strengthen the impact and generalizability of the proposed methods.
More visual insights#
More on figures

🔼 The left plot shows how CVaR0.01 (at the 0.01 quantile) of both utilitarian (USW) and egalitarian (GESW) welfare changes as the standard deviation of the Gaussian valuation distribution is increased by a scalar multiple. The right plot shows convergence time in seconds for two different optimization approaches: Iterated Quadratic Programming (Iterated QP) and Adversarial Projected Subgradient Ascent on the AAMAS 2015 dataset. The results highlight the trade-off between the accuracy and computational cost of the two approaches.
read the caption
Figure 1: Left: CVaR as noise increases for AAMAS 2015. Right: Convergence behavior of the Iterated Quadratic Program (Iterated QP) vs. Adversarial Projected Subgradient Ascent approach on AAMAS 2015.

🔼 The figure shows two plots. The left plot displays the CVaR (Conditional Value at Risk) of utilitarian social welfare (USW) and group egalitarian social welfare (GESW) as the standard deviation scale increases for the AAMAS 2015 dataset. The right plot illustrates the convergence speed of the iterated quadratic programming approach against the adversarial projected subgradient ascent method for computing robust USW on the AAMAS 2015 dataset.
read the caption
Figure 1: Left: CVaR as noise increases for AAMAS 2015. Right: Convergence behavior of the Iterated Quadratic Program (Iterated QP) vs. Adversarial Projected Subgradient Ascent approach on AAMAS 2015.
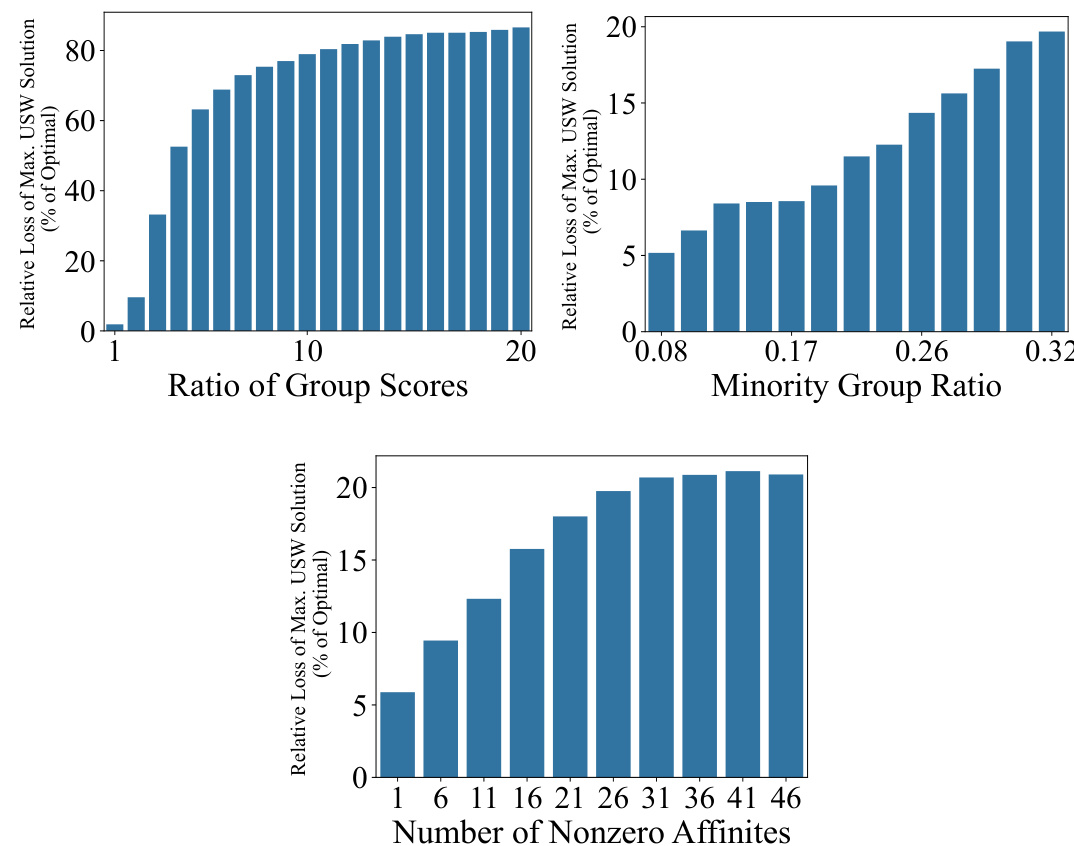
🔼 This figure shows two plots. The left plot displays how the Conditional Value at Risk (CVaR) of utilitarian and egalitarian social welfare changes as the level of noise increases in the AAMAS 2015 dataset. The right plot compares the convergence speed of two optimization algorithms: Iterated Quadratic Programming (IQP) and Adversarial Projected Subgradient Ascent, for maximizing the robust utilitarian and egalitarian welfare.
read the caption
Figure 1: Left: CVaR as noise increases for AAMAS 2015. Right: Convergence behavior of the Iterated Quadratic Program (Iterated QP) vs. Adversarial Projected Subgradient Ascent approach on AAMAS 2015.
More on tables

🔼 This table presents the performance of different allocation methods on the AAMAS 2015 dataset. Each row represents an allocation method (USW, GESW, CVaR USW, CVaR GESW, Robust USW, Robust GESW), and each column represents an evaluation metric. The values are the normalized scores, and the ± values represent the standard deviation across 5 independent runs. The table shows which allocation method performs best for each evaluation metric.
read the caption
Table 2: Performance of different allocations across each metric on the AAMAS 2015 dataset.
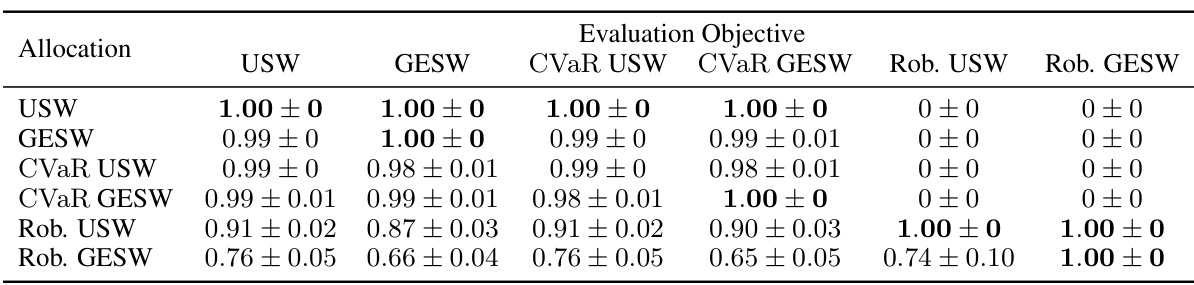
🔼 This table presents the performance of different allocation strategies across various metrics for the AAMAS 2015 dataset. Each row represents a different allocation method (e.g., maximizing utilitarian welfare (USW), maximizing group egalitarian welfare (GESW), optimizing conditional value at risk (CVaR) for USW, and robust optimization for USW and GESW). Each column shows the performance of each allocation method against the evaluation objective (USW, GESW, CVaR USW, CVaR GESW, Robust USW, Robust GESW). The values represent the normalized performance score for each allocation method, relative to the highest score achieved by any allocation in each run. This allows a direct comparison of how each method performs against various metrics and objectives.
read the caption
Table 2: Performance of different allocations across each metric on the AAMAS 2015 dataset.

🔼 This table presents the performance of different allocation strategies (USW, GESW, CVaR USW, CVaR GESW, Robust USW, Robust GESW) across various metrics on the AAMAS 2015 dataset. Each row represents an allocation strategy optimized for a specific objective, and each column shows the performance of that allocation strategy on different metrics (USW, GESW, CVaR USW, CVaR GESW, Robust USW, Robust GESW). The values are normalized to highlight that the allocation targeted for a given objective always returns the highest value on that objective.
read the caption
Table 2: Performance of different allocations across each metric on the AAMAS 2015 dataset.

🔼 This table presents the performance of different allocation strategies across various metrics on the AAMAS 2015 dataset. Each row represents a different allocation method (e.g., optimizing for USW, GESW, CVaR-USW, etc.), and each column represents a metric used to evaluate the allocation’s performance (e.g., USW, GESW, CVaR-USW, CVaR-GESW, Robust USW, Robust GESW). The values in the table represent the normalized mean performance of each allocation method across multiple runs of the experiment, with standard deviations in parentheses. This table allows for the comparison of various optimization approaches (robust, stochastic, and naive) and the corresponding performance on both utilitarian (USW) and egalitarian (GESW) welfare objectives.
read the caption
Table 2: Performance of different allocations across each metric on the AAMAS 2015 dataset.
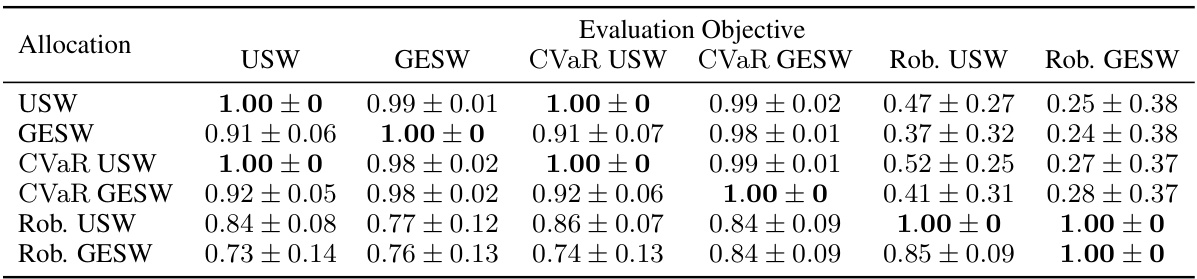
🔼 This table presents the results of an experiment evaluating different resource allocation methods on the AAMAS 2015 dataset. Each row represents a different optimization approach (e.g., maximizing utilitarian welfare (USW), maximizing group egalitarian welfare (GESW), maximizing the Conditional Value at Risk (CVaR) of USW, etc.), and each column shows the performance of the allocation generated by that method, measured according to several metrics. The metrics include the objective function value for that method (normalized to 1), and the performance of the same allocation evaluated using alternative objectives.
read the caption
Table 2: Performance of different allocations across each metric on the AAMAS 2015 dataset.

🔼 This table presents the results of an experiment evaluating different allocation methods on the AAMAS 2015 dataset. Each row represents a different allocation method (USW, GESW, CVaR USW, CVaR GESW, Robust USW, Robust GESW), aiming to optimize a specific welfare objective. Each column shows the performance of that allocation method according to various metrics (USW, GESW, CVaR USW, CVaR GESW, Robust USW, Robust GESW), which are normalized to the best performance for each metric. The table helps compare the effectiveness of different allocation methods under various fairness and robustness criteria.
read the caption
Table 2: Performance of different allocations across each metric on the AAMAS 2015 dataset.
🔼 This table summarizes the computational complexity of different optimization algorithms used to compute utilitarian and egalitarian welfare under various robustness models (linear, one ellipsoid, multiple ellipsoids, and general convex). The complexity is categorized into low (single linear program), medium (small number of linear/quadratic programs), and high (numerous quadratic programs or arbitrary concave programs). The table highlights the different algorithms’ suitability for different objective functions and uncertainty representations.
read the caption
Table 1: Summary of optimization algorithms for efficiently computing utilitarian and egalitarian welfare under different robustness concepts. Green highlights indicate problems which require solving a single linear program (low difficulty). Yellow highlights indicate solving a small number of linear or quadratic programs (medium difficulty). Red highlights indicate problems which require solving numerous quadratic programs or arbitrary concave programs.

🔼 This table summarizes the computational complexity of different optimization algorithms for computing utilitarian and egalitarian welfare under different robustness concepts (linear, one ellipsoid, multiple ellipsoids, and any arbitrary convex set). The complexity is categorized as low (single linear program), medium (small number of linear or quadratic programs), or high (numerous quadratic programs or arbitrary concave programs).
read the caption
Table 1: Summary of optimization algorithms for efficiently computing utilitarian and egalitarian welfare under different robustness concepts. Green highlights indicate problems which require solving a single linear program (low difficulty). Yellow highlights indicate solving a small number of linear or quadratic programs (medium difficulty). Red highlights indicate problems which require solving numerous quadratic programs or arbitrary concave programs.
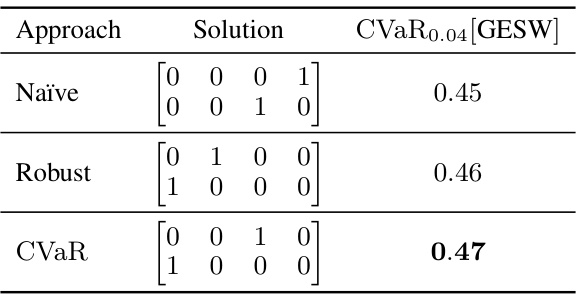
🔼 This table summarizes the computational complexity of different optimization algorithms used to solve for utilitarian and egalitarian welfare under various robustness concepts (linear, one ellipsoid, multiple ellipsoids, and general). The complexity is categorized by difficulty level (low, medium, high).
read the caption
Table 1: Summary of optimization algorithms for efficiently computing utilitarian and egalitarian welfare under different robustness concepts. Green highlights indicate problems which require solving a single linear program (low difficulty). Yellow highlights indicate solving a small number of linear or quadratic programs (medium difficulty). Red highlights indicate problems which require solving numerous quadratic programs or arbitrary concave programs.
Full paper#