TL;DR#
Finding efficient algorithms for computing equilibria in extensive-form games (EFGs) is a major challenge in AI. First-order methods (FOMs) are promising but their performance hinges on a crucial parameter: the choice of distance-generating function (DGF). The paper addresses the challenge of selecting the optimal DGF for FOMs in EFGs, noting previous approaches have relied on indirect analysis using iterate equivalence with existing algorithms. This equivalence prevents fully understanding the optimality of previous solutions and also limits the ability to refine algorithm design to leverage the chosen DGF.
This research introduces novel primal-dual treeplex norms to directly analyze the strong convexity of the weight-one dilated entropy (DilEnt) DGF. The analysis shows DilEnt achieves a near-optimal diameter-to-strong-convexity ratio, matching the state-of-the-art performance of existing algorithms (KOMWU) while offering a direct and more insightful analysis. Furthermore, a new regret lower bound is proven, confirming the near-optimality of DilEnt. The paper showcases the new analytic techniques by using them to refine the convergence rate of Clairvoyant OMD when paired with DilEnt, establishing a new state-of-the-art.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in algorithmic game theory and online learning because it identifies the optimal distance-generating function for first-order methods in extensive-form games, improving the convergence rate of algorithms. It also provides new regret bounds, enhancing our understanding of online learning’s limitations and opening avenues for further research in this area.
Visual Insights#
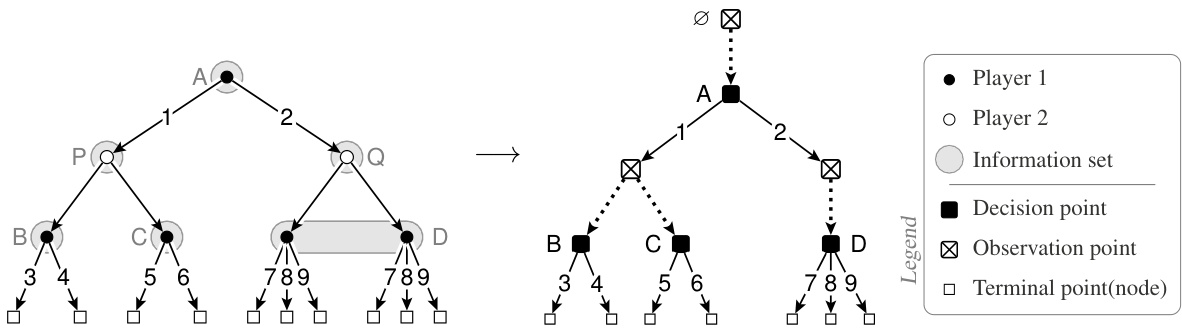
🔼 This figure shows a two-player extensive-form game and the corresponding tree-form sequential decision process (TFSDP) for player 1. The extensive-form game is represented as a game tree with nodes representing game states and branches representing actions. The TFSDP for player 1 simplifies the game by focusing solely on player 1’s decisions and information sets. Key features of the figure highlight the decision points (J), tree size (||Q||1), leaf count (||Q||1), and the number of pure strategy profiles for player 1 (|V|). The pure strategy shown, {A → 1, B → 3, C → 5}, results in a tree size of 4 and a leaf count of 2 in the TFSDP.
read the caption
Figure 1: An two-player extensive-form game and the corresponding TFSDP of player 1. The TFSDP has decision point J = {A, B, C, D}. It has tree size ||Q||1 = 4 and leaf count ||Q||₁ = 2, both given by the pure strategy {A → 1, B → 3, C → 5}. Furthermore, The player 1 has |V| = 7 pure strategy profiles in total.

🔼 This table compares the diameter-to-strong-convexity ratio (|D|/µ) of different distance-generating functions (DGFs) for extensive-form games (EFGs). It shows the ratio for Dilated Entropy, Dilated Global Entropy, and the proposed DilEnt, along with the norm pairs used and the maximum gradient norm. The table highlights that DilEnt achieves the best ratio (up to logarithmic factors).
read the caption
Table 1: Comparison of the diameter-to-strong-convexity (|D|/µ) ratio with prior results in DGFs for EFGs, where the “Norm pair” indicates the primal norm used in establishing the strong convexity, and its dual. 'Max gradient norm' indicates the maximum norm—measured in the dual of the norm with respect to which each DGF is strongly convex—of any reward vector, or the gradient of utility function, that can be encountered during optimization, assuming that all payoffs at the terminal nodes of the EFG are in the range [0, 1]. D denotes the depth of the tree, ||Q||1 the tree size (see Section 3), |A| the maximum number of actions, and |V| the number of reduced normal-form strategies. We remark that ln |V| ≤ O(||Q||1 log |A|).
In-depth insights#
Dilated Entropy#
The concept of “Dilated Entropy” emerges as a crucial regularizer within the context of first-order optimization methods used for solving extensive-form games. Its significance lies in its ability to improve the convergence rate of algorithms by optimizing the relationship between the diameter and strong convexity modulus of the strategy space. The paper highlights the optimality of dilated entropy (up to logarithmic factors) compared to other distance-generating functions. This optimality is not only theoretically proven but also demonstrates practical value through improved performance when used with online mirror descent and clairvoyant online mirror descent algorithms, leading to state-of-the-art results for approximating coarse correlated equilibria.
Regret Minimization#
Regret minimization, a core concept in online learning, focuses on minimizing the difference between an algorithm’s cumulative performance and that of the best fixed strategy in hindsight. In the context of extensive-form games, regret minimization algorithms aim to find strategies that perform well against a diverse set of opponents, iteratively improving performance over time. The paper explores various regret minimization techniques, including online mirror descent (OMD) which uses a distance-generating function to efficiently find approximate equilibria. The choice of distance-generating function significantly impacts the algorithm’s performance, and the paper analyzes the properties of dilated entropy and its variants for optimizing OMD. Lower bounds on achievable regret are derived, showing the near-optimality of dilated entropy up to logarithmic factors. This optimality analysis demonstrates that DilEnt is computationally efficient and theoretically sound.
Treeplex Norms#
The concept of “Treeplex Norms” in the context of extensive-form game solving is intriguing. It suggests a novel approach to analyzing the strong convexity of distance-generating functions (DGFs), a critical component for the efficiency of first-order optimization methods. The paper likely introduces novel primal and dual norms tailored to the tree-like structure of extensive-form games, which should facilitate the analysis of algorithms like online mirror descent (OMD). This approach is significant because standard analysis techniques often struggle to capture the nuances of such structured spaces. The use of treeplex norms seems intended to provide a more natural analytical framework that is better suited to the recursive structure of the game tree, potentially yielding tighter bounds on strong convexity and improved convergence rate guarantees for algorithms used to find approximate equilibria. The success of this approach hinges on the ability of the treeplex norms to offer a tighter characterization of the geometry of the strategy space, leading to a more refined analysis of optimization algorithms within that space. Further research could investigate the generality of treeplex norms and explore their application in other tree-structured problems.
EFG Optimality#
The concept of “EFG Optimality” in the context of extensive-form games (EFGs) centers on identifying the optimal algorithms and strategies for solving these complex games. First-order methods (FOMs) are often employed, relying on a distance-generating function (DGF) to regularize the strategy space. Research focuses on determining the ideal DGF, as the ratio between its strong convexity and diameter significantly impacts FOM performance. Dilated entropy (DilEnt) emerges as a prominent candidate, exhibiting iterate equivalence with state-of-the-art algorithms like KOMWU. However, a key contribution is the introduction of novel primal-dual treeplex norms, providing a refined analytical framework to demonstrate DilEnt’s near-optimality, up to logarithmic factors, in terms of its diameter-to-strong-convexity ratio. This optimality is further solidified by matching regret lower bounds, showing that DilEnt is not just efficient but nearly optimal for solving EFGs using FOMs.
Lower Bounds#
The section on lower bounds is crucial for establishing the optimality of the proposed Dilated Entropy (DilEnt) regularizer. It rigorously demonstrates that no algorithm can achieve significantly better regret than DilEnt, thereby validating its near-optimal performance. The authors derive a lower bound on the regret, showcasing that any algorithm solving extensive-form games must incur regret at least within a logarithmic factor of DilEnt’s bound. This result is particularly important because it directly addresses the core claim of the paper, which posits DilEnt’s near-optimality. The lower bound proof leverages a carefully constructed hard instance, highlighting the fundamental limitations in online learning for this problem. A matching upper bound further strengthens the overall argument, showing that DilEnt’s performance is essentially the best achievable up to a logarithmic factor. This rigorous analysis provides a strong theoretical underpinning for the practical efficacy of DilEnt.
More visual insights#
More on figures

🔼 This figure shows a simple two-player extensive-form game and the corresponding tree-form sequential decision process (TFSDP) for player 1. The extensive-form game is represented as a game tree, illustrating the sequence of actions and decisions. The TFSDP simplifies the representation from player 1’s perspective, focusing on their decision points (information sets), actions, and the resulting observation points. The caption highlights key metrics derived from the TFSDP: tree size, leaf count, and the number of pure strategy profiles. These metrics quantify aspects of the game’s complexity.
read the caption
Figure 1: An two-player extensive-form game and the corresponding TFSDP of player 1. The TFSDP has decision point J = {A, B, C, D}. It has tree size ||Q||1 = 4 and leaf count ||Q||₁ = 2, both given by the pure strategy {A → 1, B → 3, C → 5}. Furthermore, The player 1 has |V| = 7 pure strategy profiles in total.
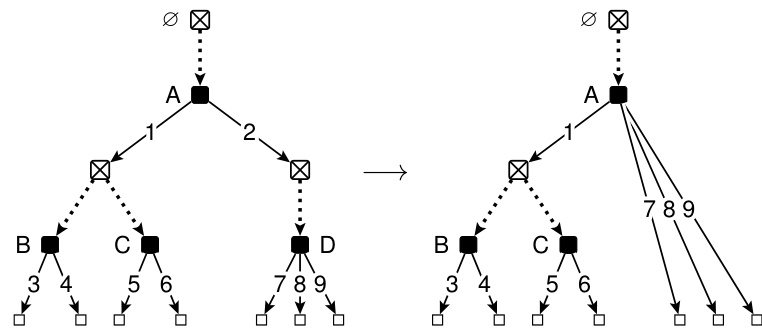
🔼 This figure shows a two-player extensive-form game and its corresponding tree-form sequential decision process (TFSDP) for Player 1. The extensive-form game is represented as a game tree with nodes representing game states and edges representing actions. The TFSDP simplifies Player 1’s perspective, highlighting their decision points (J), the actions they can take at each point, and the resulting terminal nodes. Key metrics illustrating the game’s complexity are also given: the tree size (||Q||1), the leaf count (||Q||1), and the number of pure strategy profiles for Player 1 (|V|).
read the caption
Figure 1: An two-player extensive-form game and the corresponding TFSDP of player 1. The TFSDP has decision point J = {A, B, C, D}. It has tree size ||Q||1 = 4 and leaf count ||Q||₁ = 2, both given by the pure strategy {A → 1, B → 3, C → 5}. Furthermore, The player 1 has |V| = 7 pure strategy profiles in total.
Full paper#



















