TL;DR#
Federated learning (FL) faces challenges with heterogeneous data domains, where data from different sources have varied feature distributions. Existing Federated Prototype Learning (FedPL) methods often fail to account for this variance, leading to performance gaps between clients and domains. This is a significant challenge because non-IID data is the norm, not the exception, in most real-world applications of federated learning.
FedPLVM, presented in this paper, proposes a novel solution by introducing a dual-level prototype clustering mechanism and an a-sparsity prototype loss. The dual-level clustering creates both local and global prototypes, reducing communication costs and preserving privacy. The a-sparsity loss mitigates the unequal learning challenges by enhancing intra-class similarity while reducing inter-class similarity, especially for underrepresented domains. Experiments on Digit-5, Office-10, and DomainNet demonstrate FedPLVM’s superiority over existing approaches, highlighting its effectiveness in addressing real-world data heterogeneity issues.
Key Takeaways#
Why does it matter?#
This paper is important because it tackles the critical challenge of data heterogeneity in federated learning, a common issue hindering the widespread adoption of this privacy-preserving technique. By proposing FedPLVM, a novel approach that effectively addresses cross-domain variance, the research opens new avenues for improving the performance and fairness of federated learning models in real-world applications. This is highly relevant to current trends in FL research, particularly in addressing non-IID data distributions and domain adaptation. Further exploration of FedPLVM’s techniques such as dual-level prototype clustering and a-sparsity prototype loss could also lead to advances in related fields like few-shot learning and transfer learning.
Visual Insights#

🔼 This figure compares the Vanilla and Proposed approaches of Federated Prototype Learning (FedPL) in heterogeneous data domains. Vanilla FedPL directly averages local feature distributions to create prototypes, while the proposed approach uses a dual-level clustering method (local and global) to improve prototype quality by capturing data variance. The visualization shows how the proposed method better separates different classes (larger inter-class distance, smaller intra-class distance), especially in the ‘harder’ domains where data is less cleanly separated.
read the caption
Figure 1: Illustration of federated learning with heterogeneous data domains. The Vanilla column depicts the local feature distribution of the standard FedPL approach, obtaining average local and global prototypes directly. Proposed method showcased in the adjacent column yields a larger inter-class distance and a reduced intra-class distance. Note that without capturing variance information, even for hard domains, local averaged prototypes for each class can be well distinguished while the feature vectors are still mixed up. Both methods illustrate noticeable variations in domain characteristics across datasets, as detailed in Fig. 4.
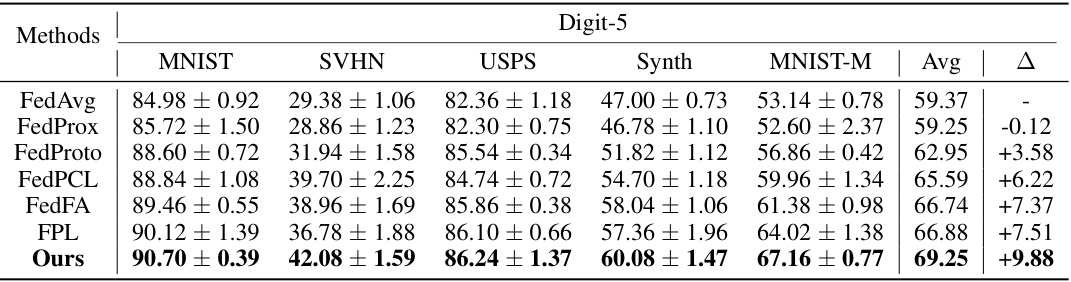
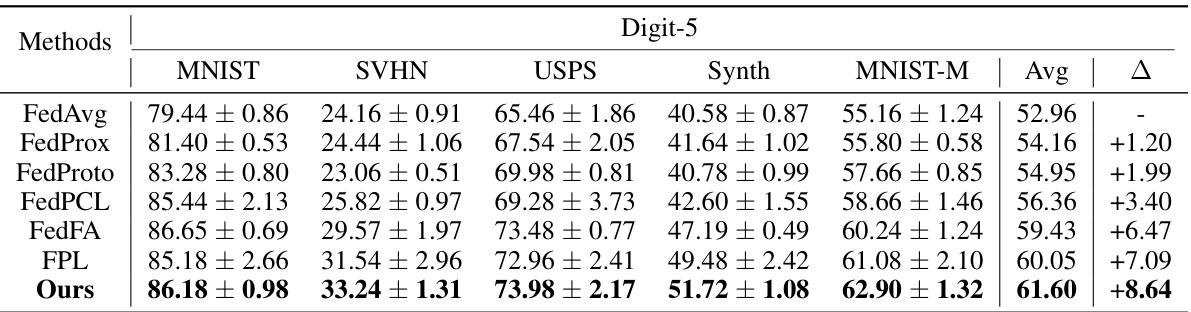
🔼 This table presents the test accuracy results for different federated learning methods on the Digit-5 dataset. The methods compared include FedAvg, FedProx, FedProto, FedPCL, FedFA, FPL, and the proposed FedPLVM method. The accuracy is reported for each of the five domains within Digit-5 (MNIST, SVHN, USPS, Synth, MNIST-M) and as an average across all domains. The Δ column shows the improvement of each method compared to the baseline FedAvg method.
read the caption
Table 1: Test accuracy on Digit-5. Avg means average results among all clients. Details in Sec. 5.1.
In-depth insights#
FedPL Variance Issue#
The core issue in Federated Prototype Learning (FedPL) lies in managing the variance of feature representations across diverse client domains. Standard FedPL methods often compute average prototypes, failing to capture the intra-domain variance, particularly in complex datasets. This leads to performance disparities between clients with easy-to-learn and hard-to-learn domains. Cross-domain representation variance becomes a significant obstacle for effective model generalization. Unequal learning challenges arise because methods fail to account for the varying richness of feature distribution information among clients. Addressing this requires techniques that effectively capture and leverage both local and global variance information, enabling fairer learning across clients and enhanced model robustness. This means that methods must go beyond simply averaging features to represent clients fairly and accurately.
Dual Proto Clustering#
Dual Prototype Clustering is a novel approach to enhance Federated Prototype Learning (FPL) models by addressing the limitations of single-level prototype generation. It introduces a two-step clustering process: first, local clustering on individual client devices to capture data variance within each domain; then, global clustering on the server to consolidate and reduce communication overhead. This dual-level strategy is particularly useful in handling heterogeneous data domains, where each client’s data distribution is unique. By capturing local variance before aggregating prototypes, the method mitigates the negative effects of unequal data distributions that hinder the accuracy and fairness of FPL, enabling better generalization of the model to unseen data from various sources. The method also improves the privacy of the data by limiting the number of prototypes transferred between the clients and the central server. This technique is computationally efficient and privacy-preserving, making it particularly well-suited for real-world federated learning applications.
Alpha-Sparsity Loss#
The proposed alpha-sparsity loss function is a novel approach to address the challenge of overlapping feature representations in multi-prototype learning. It cleverly modifies the cosine similarity metric by raising it to the power of alpha (0 < alpha < 1), thereby amplifying inter-class distances while mitigating intra-class distances. This variance-aware approach enhances the sparsity of inter-class feature distributions, leading to improved prototype distinctiveness and model generalization. The addition of a corrective term further refines the loss function by counterbalancing the effect of alpha and ensuring that prototypes retain sufficient intra-class similarity. The alpha-sparsity loss is a significant improvement over traditional methods that fail to effectively address prototype overlap issues, thereby contributing to more robust model performance in challenging heterogeneous data environments. This methodology effectively uses alpha as a tuning parameter to control the level of sparsity. Combining this loss with dual-level clustering demonstrates a notable advancement in federated prototype learning, demonstrating its efficacy in mitigating cross-domain representation variance.
DomainNet Results#
Analyzing hypothetical “DomainNet Results” in a research paper necessitates a nuanced approach. A thoughtful summary would delve into the specific metrics used to evaluate performance (e.g., accuracy, F1-score, precision/recall), comparing the proposed method against established baselines on DomainNet’s diverse domains. Key observations would include whether the new method shows consistent improvement across all domains or if performance varies significantly depending on the nature of the data. A crucial aspect is the extent to which the new method handles domain shift—a core challenge in DomainNet’s heterogeneous datasets. The analysis should quantify the extent of improvement, highlighting statistically significant gains where appropriate. Furthermore, the discussion should acknowledge any limitations, such as computational cost or memory requirements that might affect the new method’s practical applicability. Finally, it’s vital to understand how the results on DomainNet contribute to the paper’s overall claims about the method’s efficacy in cross-domain scenarios. Emphasis should be given to demonstrating the method’s generalization ability and robustness to domain variations.
Future of FedPLVM#
The future of FedPLVM lies in addressing its limitations and exploring new avenues for improvement. Extending its applicability to a wider range of data modalities beyond images and text is crucial. This would involve adapting the prototype clustering mechanism to handle various data types and developing robust loss functions that can effectively leverage unique data characteristics. Improving efficiency in communication and computation is also key, especially for deployment in resource-constrained settings. This could involve exploring techniques like model compression, quantization, or federated transfer learning. Further research should focus on enhancing privacy and security, potentially through the use of differential privacy mechanisms or homomorphic encryption. Moreover, investigating the impact of varying data distributions and noise levels on the algorithm’s performance is essential. Understanding these factors and developing robust mitigation strategies would significantly improve the practicality and reliability of FedPLVM in real-world applications. Finally, exploring the combination of FedPLVM with other FL techniques, such as contrastive learning or data augmentation, holds the promise of further enhancing the algorithm’s capabilities and broadening its applications.
More visual insights#
More on figures

🔼 This figure illustrates the FedPLVM framework’s workflow. It begins with clients generating sample embeddings using feature extractors. These embeddings undergo local clustering to create local clustered prototypes. The server then collects these prototypes, performs global clustering to generate global clustered prototypes, and averages client models to create a global model. Finally, the global model and clustered prototypes are sent back to the clients for local model training using the α-sparsity prototype loss (La) and cross-entropy loss (LCE).
read the caption
Figure 2: An overview of our proposed FedPLVM framework. Once the sample embedding is generated by the feature extractor, the client conducts the first-level local clustering, following Eq. 3. Subsequently, the server gathers all local clustered prototypes and local models (comprising feature extractors and classifiers), initiates the second-level global clustering based on Eq. 4, and averages the local models to form a global model. Finally, clients utilize the received global clustered prototypes to update the local model, employing loss functions La from Eq. 5 and LCE from Eq. 9.

🔼 This figure compares three different prototype generation methods using t-SNE visualization. The first method averages features locally and then globally. The second method averages features locally but clusters prototypes globally. The third method (the proposed method) clusters features locally and globally. The ‘Total’ column shows a visualization of all the data combined, highlighting the differences in feature distribution across methods.
read the caption
Figure 3: Visualization of different prototype generation methods. The first row averages feature vectors locally and averages local prototypes globally. The second row averages feature vectors locally and clusters local prototypes globally. The last row (ours) clusters feature vectors locally and clusters local clustered prototypes globally. The last column Total is the visualization of mixing the feature vectors from all datasets. Details in Sec. 5.2.1.
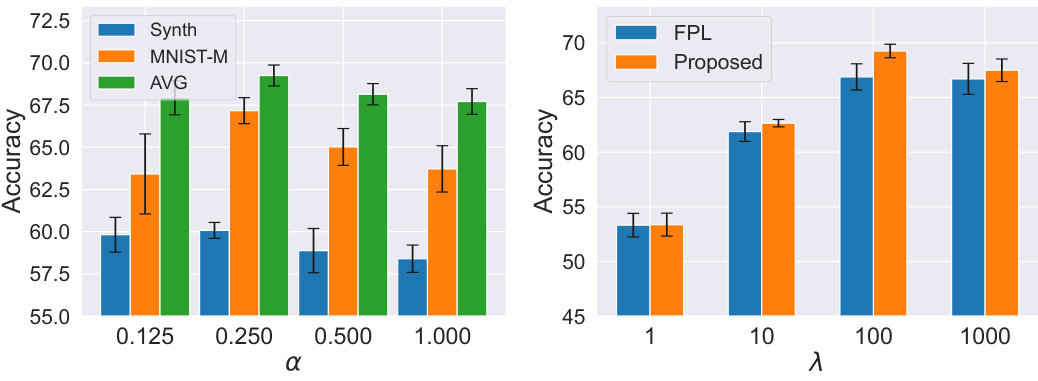
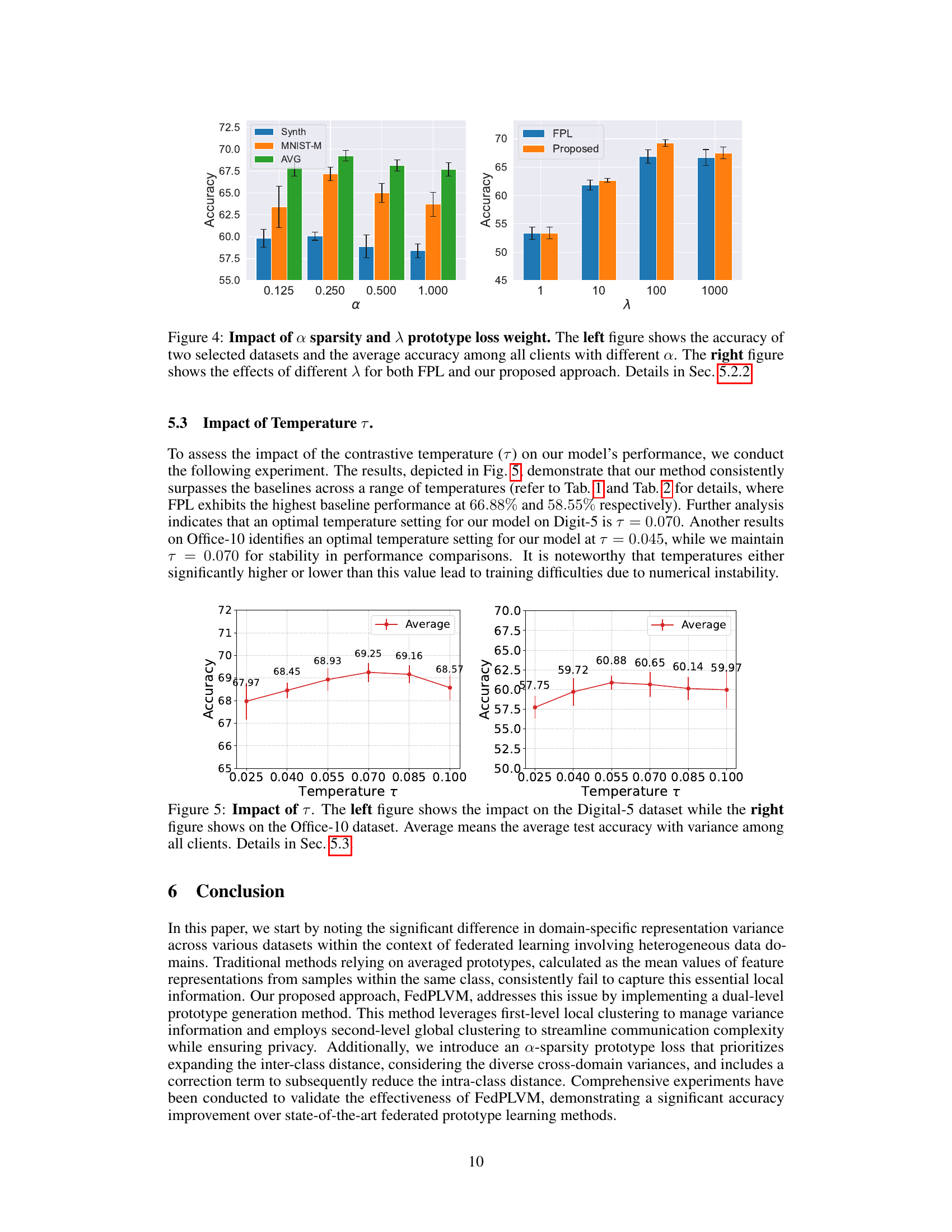
🔼 This figure shows the impact of hyperparameters α and λ on the performance of the proposed FedPLVM model. The left subplot illustrates how different values of α (a sparsity parameter in the α-sparsity prototype loss) affect the accuracy on two selected datasets (Synth and MNIST-M) and the average accuracy across all clients. The right subplot compares the performance of the proposed method and FPL model (a baseline method) across various values of λ (the weight balancing between the α-sparsity loss and the cross-entropy loss).
read the caption
Figure 4: Impact of a sparsity and λ prototype loss weight. The left figure shows the accuracy of two selected datasets and the average accuracy among all clients with different α. The right figure shows the effects of different λ for both FPL and our proposed approach. Details in Sec. 5.2.2.
🔼 This figure visualizes the different prototype generation methods used in the paper. It compares three methods: averaging feature vectors locally and globally; averaging locally and clustering globally; and clustering locally and globally. The visualization shows how different prototype generation approaches affect the distribution of feature vectors, particularly highlighting the improvement of the proposed dual-level clustering approach in separating features from different classes and domains.
read the caption
Figure 3: Visualization of different prototype generation methods. The first row averages feature vectors locally and averages local prototypes globally. The second row averages feature vectors locally and clusters local prototypes globally. The last row (ours) clusters feature vectors locally and clusters local clustered prototypes globally. The last column Total is the visualization of mixing the feature vectors from all datasets. Details in Sec. 5.2.1.
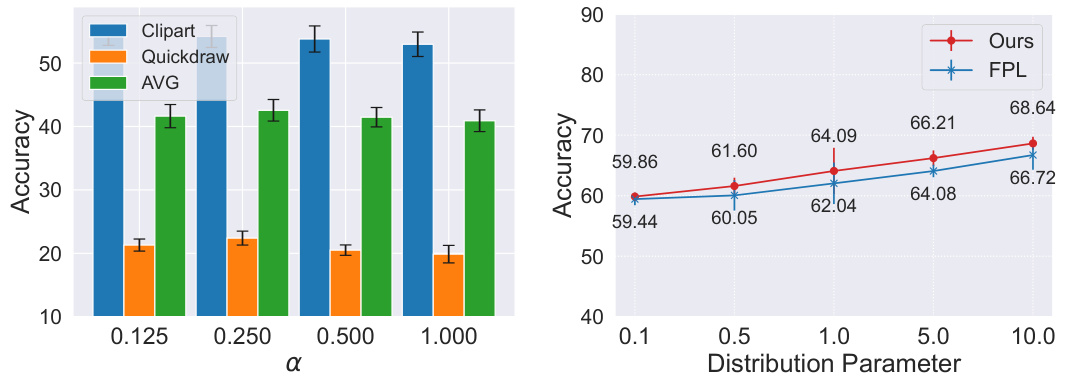
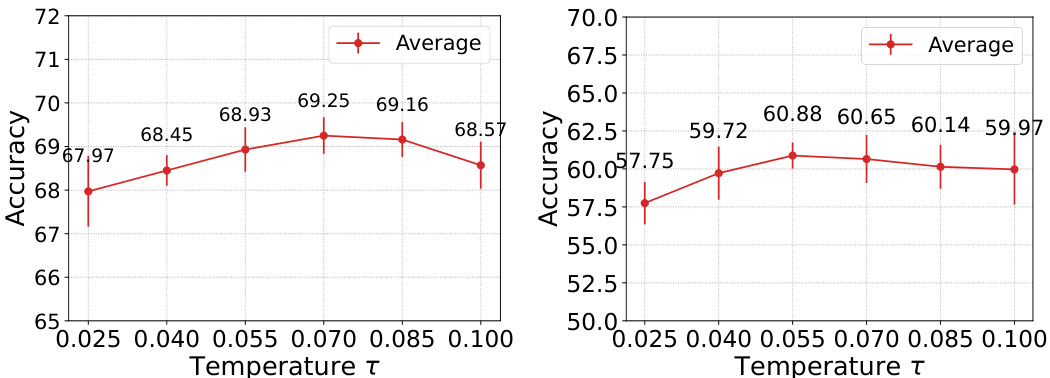
🔼 This figure demonstrates the impact of two hyperparameters, α (alpha) and λ (lambda), on the performance of the proposed FedPLVM model. The left subplot shows how the accuracy varies across different α values for three different datasets (Clipart, Quickdraw, and the average across all datasets). The right subplot compares the performance of FedPLVM and another model (FPL) at different values of λ, demonstrating the sensitivity of model accuracy to this parameter.
read the caption
Figure 4: Impact of a sparsity and λ prototype loss weight. The left figure shows the accuracy of two selected datasets and the average accuracy among all clients with different α. The right figure shows the effects of different λ for both FPL and our proposed approach. Details in Sec. 5.2.2.
🔼 This figure compares three different prototype generation methods in federated prototype learning with heterogeneous data domains. The methods differ in how they handle local and global prototypes. The first method averages feature vectors locally and then averages the resulting local prototypes to get global prototypes. The second method averages feature vectors locally, then clusters the local prototypes to obtain global prototypes. The third method, proposed by the authors, first clusters feature vectors locally and then clusters the local clustered prototypes to get the global prototypes. The visualization shows that the authors’ method leads to better separation of features in each domain, likely improving model performance.
read the caption
Figure 3: Visualization of different prototype generation methods. The first row averages feature vectors locally and averages local prototypes globally. The second row averages feature vectors locally and clusters local prototypes globally. The last row (ours) clusters feature vectors locally and clusters local clustered prototypes globally. The last column Total is the visualization of mixing the feature vectors from all datasets. Details in Sec. 5.2.1.
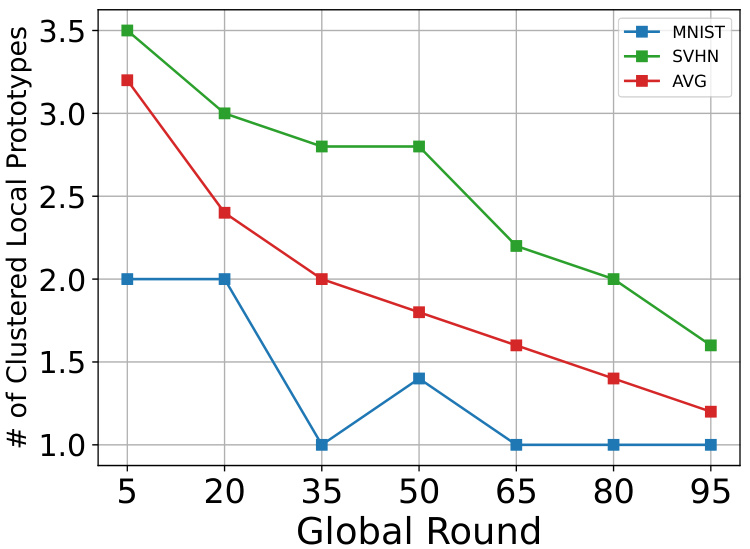
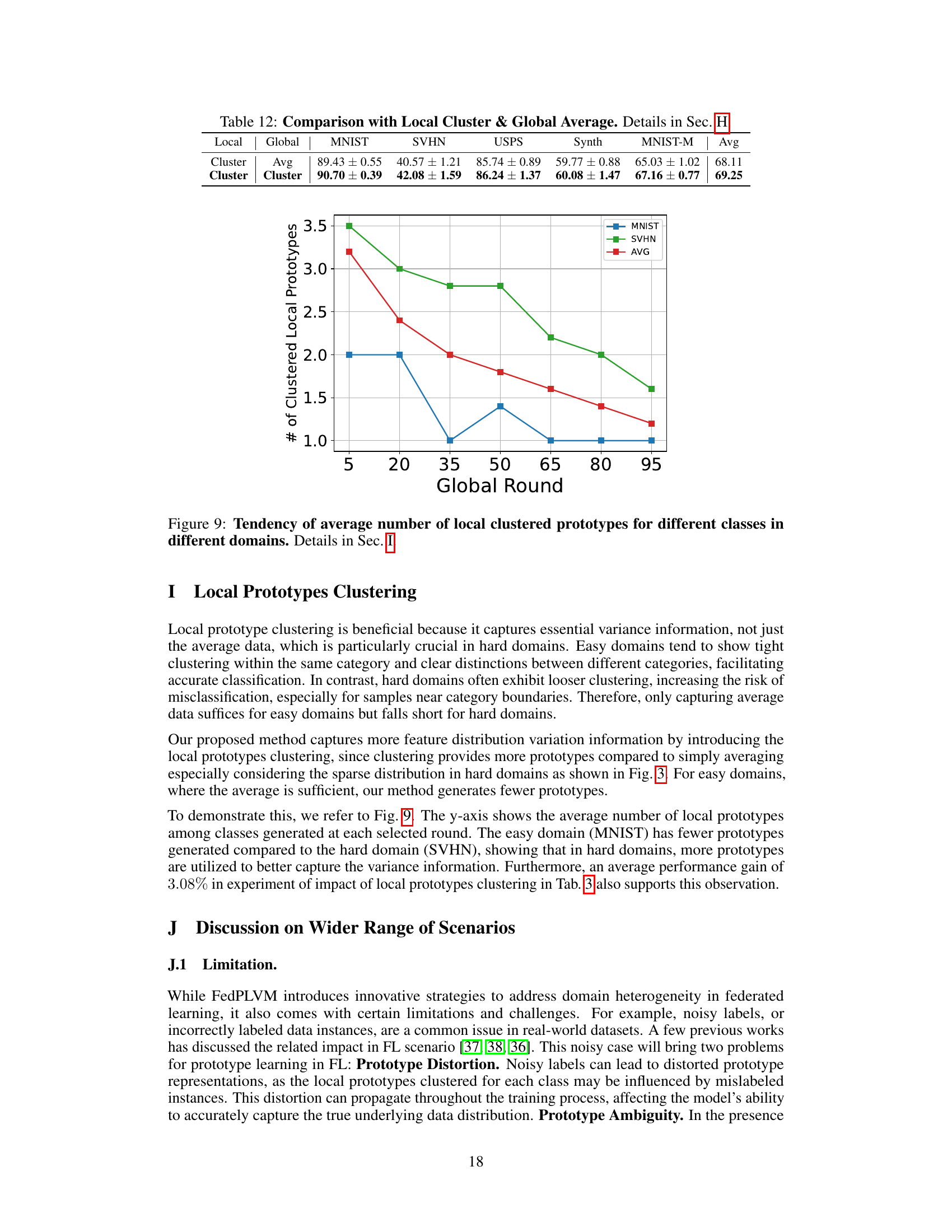
🔼 This figure shows how the average number of local clustered prototypes changes over global rounds for different classes (MNIST, SVHN, and the average across all classes) in different domains. It demonstrates that the number of prototypes tends to decrease as the global round progresses, but the rate of decrease varies across classes and datasets. The easy dataset MNIST has consistently fewer local prototypes than the hard dataset SVHN, suggesting that more prototypes are needed to capture the complexity of the hard dataset. This is relevant to section I which discusses the impact of Local Prototype Clustering, showing that the number of local prototypes is dynamically adjusted based on the data distribution and domain complexity.
read the caption
Figure 9: Tendency of average number of local clustered prototypes for different classes in different domains. Details in Sec. I.
More on tables
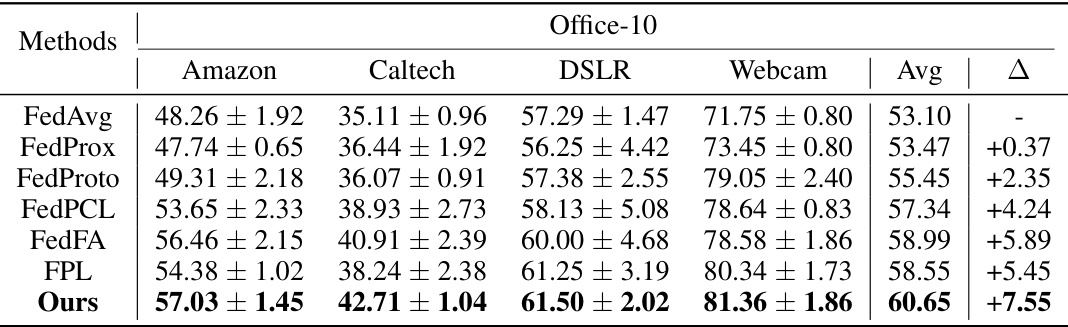
🔼 This table presents the test accuracy results of different federated learning methods on the Office-10 dataset. The results are broken down by individual dataset (Amazon, Caltech, DSLR, Webcam) and provide the average accuracy across all datasets. The Δ column shows the improvement in average accuracy compared to the FedAvg baseline.
read the caption
Table 2: Test accuracy on Office-10. Details in Sec. 5.1.

🔼 This table compares three different prototype generation methods: averaging local and global prototypes, averaging local prototypes and clustering global prototypes, and clustering local and global prototypes. The results show that clustering at both the local and global levels yields the best performance, as indicated by the highest average accuracy and lowest variance. This highlights the importance of capturing variance information in prototype generation for improved performance in federated learning with heterogeneous data domains.
read the caption
Table 3: Comparison on prototype generation methods. Variance means the average distance from the normalized feature vector of one sample to its corresponding class feature center (i.e. the averaged prototype). Results are then used for visualization in Fig. 3. Details in Sec. 5.2.1.

🔼 This table compares the performance of FedPLVM with and without global clustering. The ‘w/o’ row shows results where the server sends all local clustered prototypes to each client. The ‘w/’ row shows results where global clustering is used to reduce the number of prototypes sent. The table shows that using global clustering improves performance while significantly reducing communication costs and improving privacy.
read the caption
Table 4: Comparison between w/o and w/ global clustering. w/o means the server distributes all local clustered prototypes to the clients for local training. Avg # of prototypes is the average number of prototypes each client receives from the server during each global round. Details in Sec. 5.2.1.
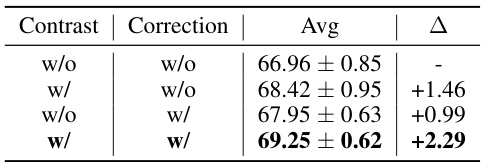
🔼 This table presents the ablation study results on the impact of different components of the α-sparsity prototype loss. It compares the performance when using only the contrastive term, only the correction term, neither term, and both terms. The results show the average accuracy across all clients for each configuration and the improvement achieved by adding each component.
read the caption
Table 5: Comparison on components of α-sparsity prototype loss. Contrast and Correction stand for the contrastive and corrective loss term in the total α-sparsity loss respectively. Avg is the average accuracy result for all clients. Details in Sec. 5.2.2.
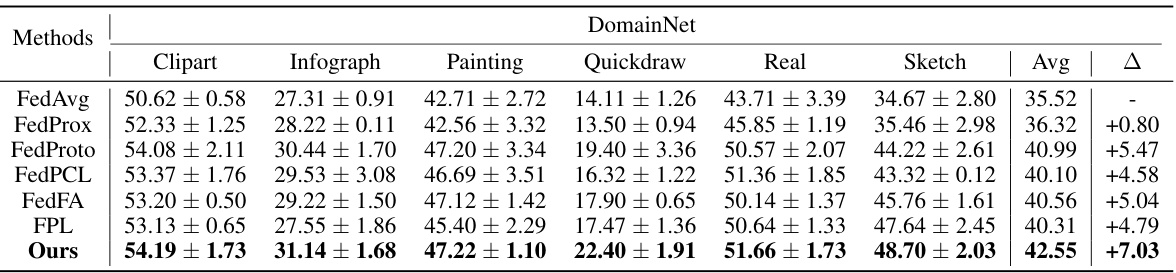
🔼 This table presents the test accuracy results on the DomainNet dataset for different federated learning methods. It shows the average accuracy across all clients for each of the six domains within DomainNet (Clipart, Infograph, Painting, Quickdraw, Real, Sketch) and the overall average accuracy. The delta (Δ) column indicates the improvement in average accuracy compared to the FedAvg baseline.
read the caption
Table 6: Test accuracy on DomainNet. Details in Sec. 5.1.
🔼 This table presents the test accuracy results for different federated learning methods on the Digit-5 dataset under a non-i.i.d. label setting, which is a scenario where data is not independently and identically distributed across clients. The Dirichlet distribution with parameter α=0.5 is used to generate the non-i.i.d. data. The table shows the average test accuracy across all clients for each method and also shows the difference in average accuracy compared to the baseline FedAvg method (Δ column). The results are broken down by individual dataset (MNIST, SVHN, USPS, Synth, MNIST-M) within Digit-5.
read the caption
Table 7: Test accuracy on Digit-5 under label non-i.i.d. setting. Avg means average results among all clients. We apply the Dirichlet method (α = 0.5) to obtain the data distribution and create the non-i.i.d. dataset for each client. Details in Sec. D.

🔼 This table presents the test accuracy results for the Office-10 dataset. The results are shown for different methods, including FedAvg, FedProx, FedProto, FedPCL, FedFA, FPL, and the proposed method (Ours). The accuracy is reported for each of the four domains in Office-10 (Amazon, Caltech, DSLR, and Webcam), as well as the average accuracy across all domains. The Δ column shows the improvement of each method compared to FedAvg. Section 5.1 provides further details on the experimental setup.
read the caption
Table 2: Test accuracy on Office-10. Details in Sec. 5.1.

🔼 This table compares the performance of the proposed FedPLVM method using FINCH clustering with the performance using K-Means clustering. The adaptive K-means approach uses the number of clusters determined by FINCH as the K value for K-Means. The table shows that while carefully tuned K-means can achieve similar results, poorly tuned K-means performs worse than FINCH, highlighting the advantage of the parameter-free FINCH algorithm used in the paper.
read the caption
Table 9: Comparison with K-Means Algorithm. Adaptive K means we use the number of clustering centers from FINCH as K. Details in Sec. E.

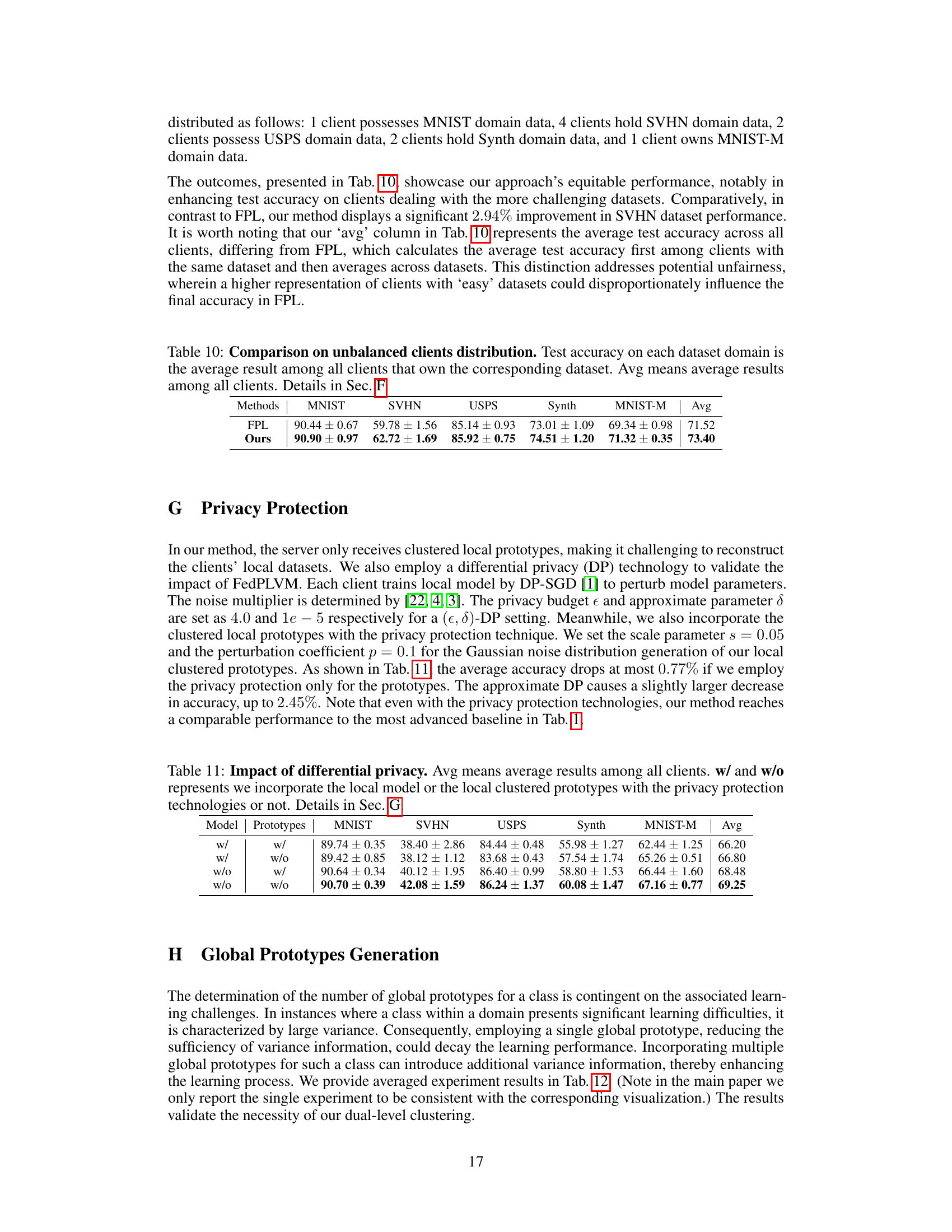
🔼 This table presents the results of the experiment conducted with unbalanced client data distribution. The goal is to showcase FedPLVM’s performance in a more realistic scenario where some domains have many more clients than others. The table shows the average accuracy across all clients for each domain (MNIST, SVHN, USPS, Synth, MNIST-M). The ‘Avg’ column provides the overall average accuracy across all domains and clients. This is compared to FPL to demonstrate FedPLVM’s improved fairness and robustness in dealing with uneven client representation across different data domains.
read the caption
Table 10: Comparison on unbalanced clients distribution. Test accuracy on each dataset domain is the average result among all clients that own the corresponding dataset. Avg means average results among all clients. Details in Sec. F.

🔼 This table presents the results of an ablation study evaluating the impact of differential privacy on the model’s performance. Four scenarios are compared: 1) both the model and prototypes use differential privacy, 2) only the model uses differential privacy, 3) only the prototypes use differential privacy, and 4) neither use differential privacy. The results show the average test accuracy across five datasets (MNIST, SVHN, USPS, Synth, MNIST-M) for each scenario, illustrating the trade-off between privacy and accuracy.
read the caption
Table 11: Impact of differential privacy. Avg means average results among all clients. w/ and w/o represents we incorporate the local model or the local clustered prototypes with the privacy protection technologies or not. Details in Sec. G.

🔼 This table presents the test accuracy results for five different digit recognition datasets (MNIST, SVHN, USPS, Synth, MNIST-M) using various federated learning methods. The ‘Avg’ column represents the average test accuracy across all datasets. The ‘Δ’ column shows the improvement in average accuracy compared to the FedAvg baseline. Section 5.1 provides more detailed explanations of the experimental setup and results.
read the caption
Table 1: Test accuracy on Digit-5. Avg means average results among all clients. Details in Sec. 5.1.
Full paper#