TL;DR#
Understanding why deep neural networks (DNNs) generalize well remains a challenge. Existing generalization bounds often rely on continuous-time dynamics or restrictive assumptions, limiting their practical use. Also, methods leveraging trajectory topology for generalization prediction typically assume continuous or infinite training, hindering practical estimation.
This work introduces new topology-based complexity measures to address these limitations. Instead of continuous-time assumptions, the researchers directly use the discrete nature of training trajectories. Their measures provably bound generalization error, correlate strongly with empirical performance in various DNNs, and are computationally efficient. The flexible framework easily extends to different tasks, architectures, and domains.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in machine learning and topology because it bridges the gap between theoretical generalization bounds and practical applications. It provides novel, computationally efficient topological measures that strongly correlate with generalization performance, surpassing existing methods. This opens up new avenues for understanding and improving model generalization, impacting various fields that use deep neural networks.
Visual Insights#
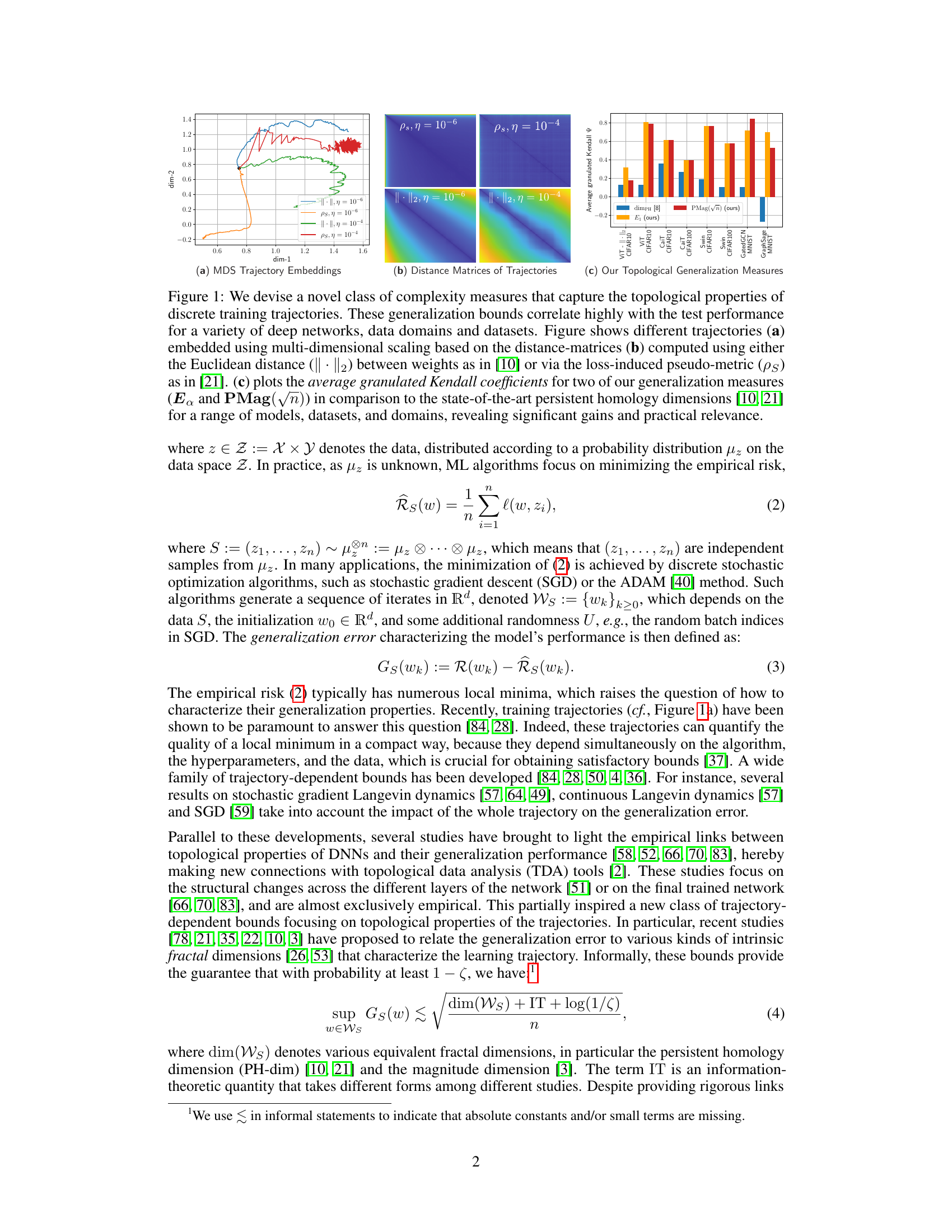
🔼 This figure demonstrates the effectiveness of the proposed topological complexity measures for predicting generalization performance. Panel (a) shows multi-dimensional scaling (MDS) embeddings of training trajectories for various models and optimizers. Panel (b) displays distance matrices computed using two different metrics: Euclidean distance and a loss-induced pseudo-metric. Finally, panel (c) presents a comparison of the average granulated Kendall correlation coefficients between the topological complexity measures and the generalization error, highlighting the superior performance of the proposed measures compared to state-of-the-art methods.
read the caption
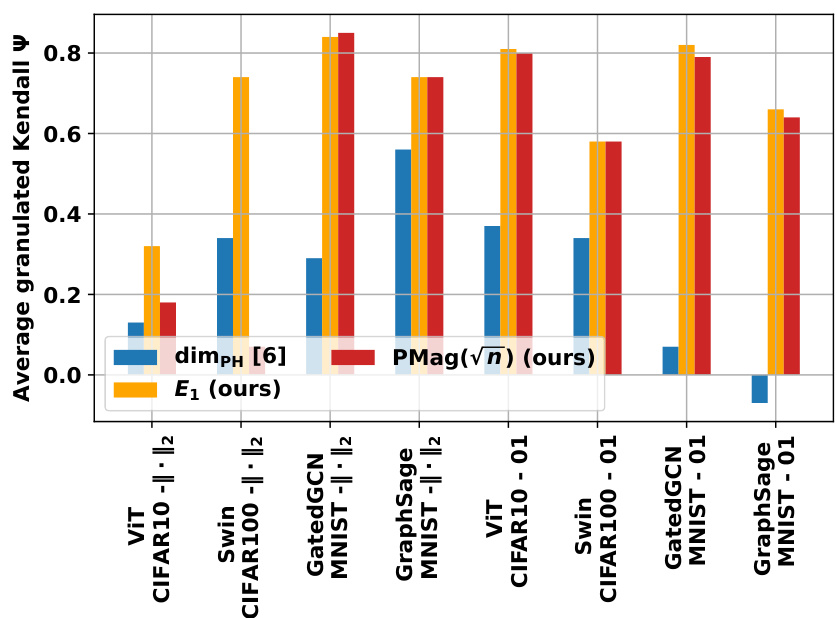
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
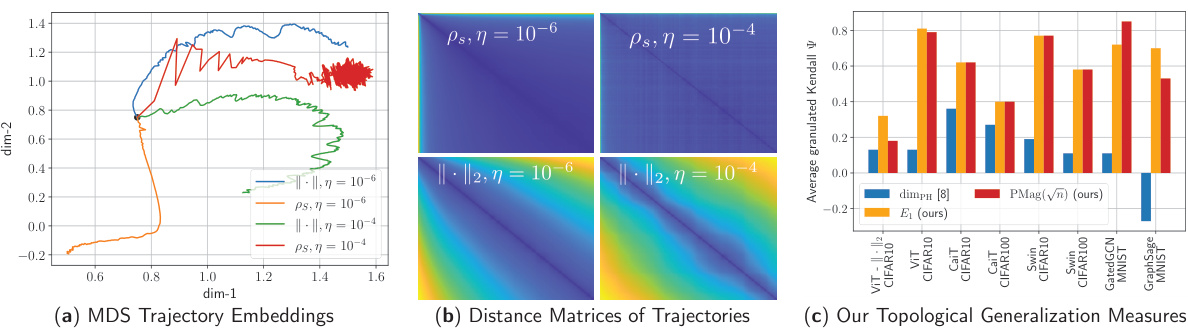
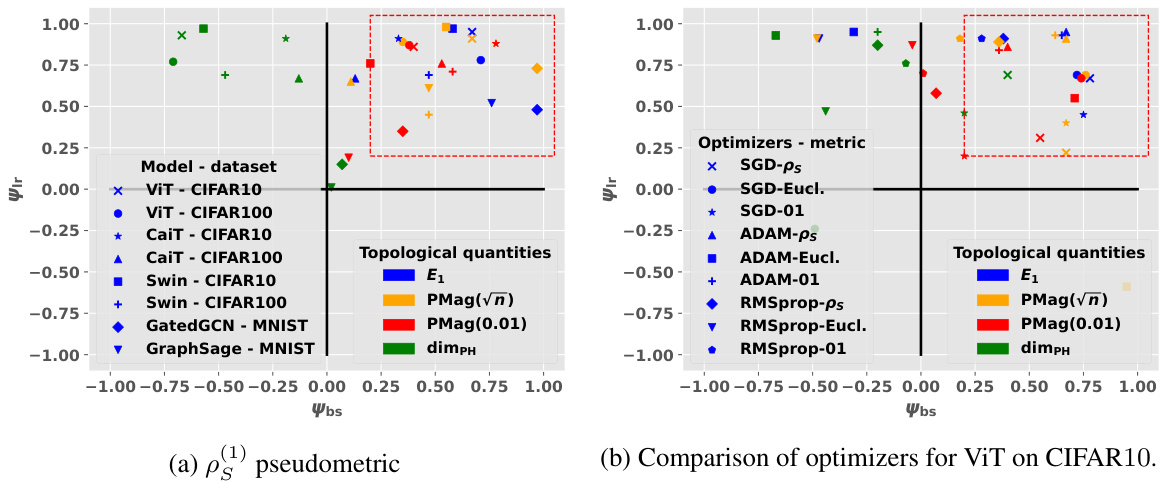
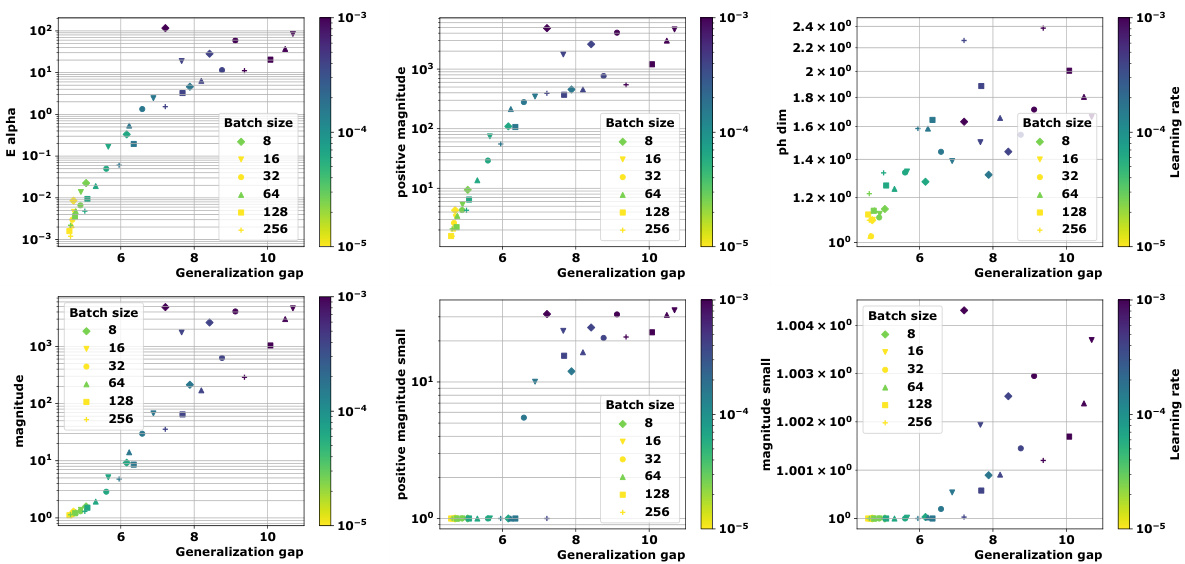
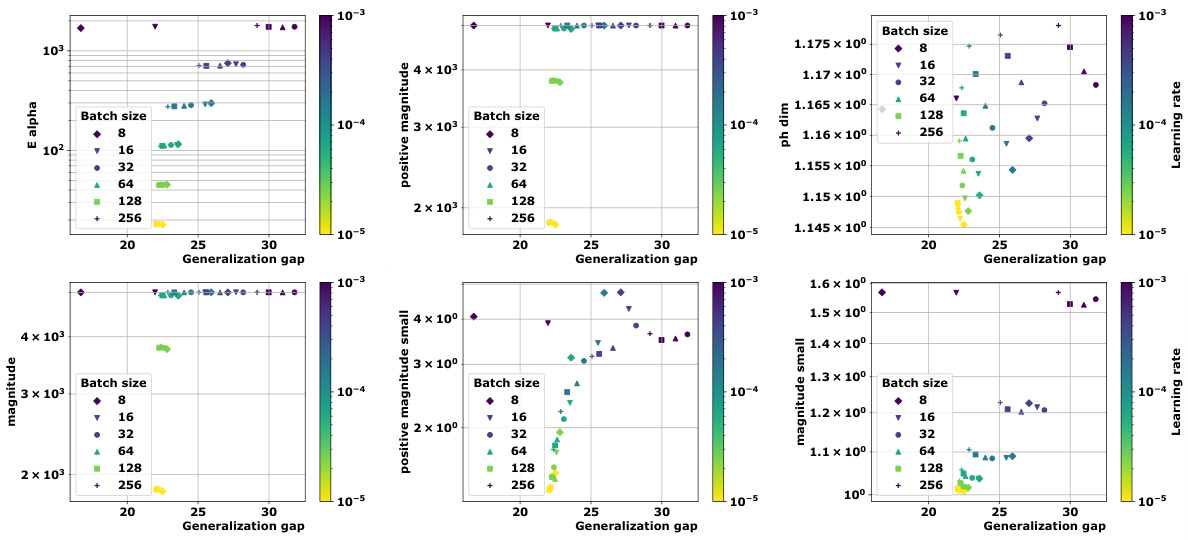
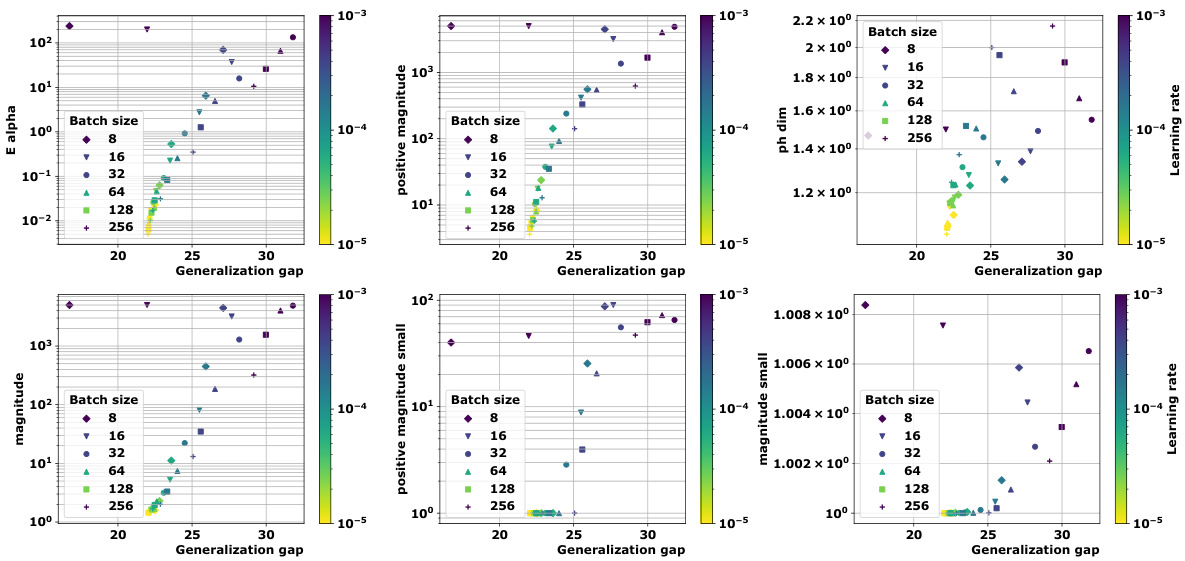
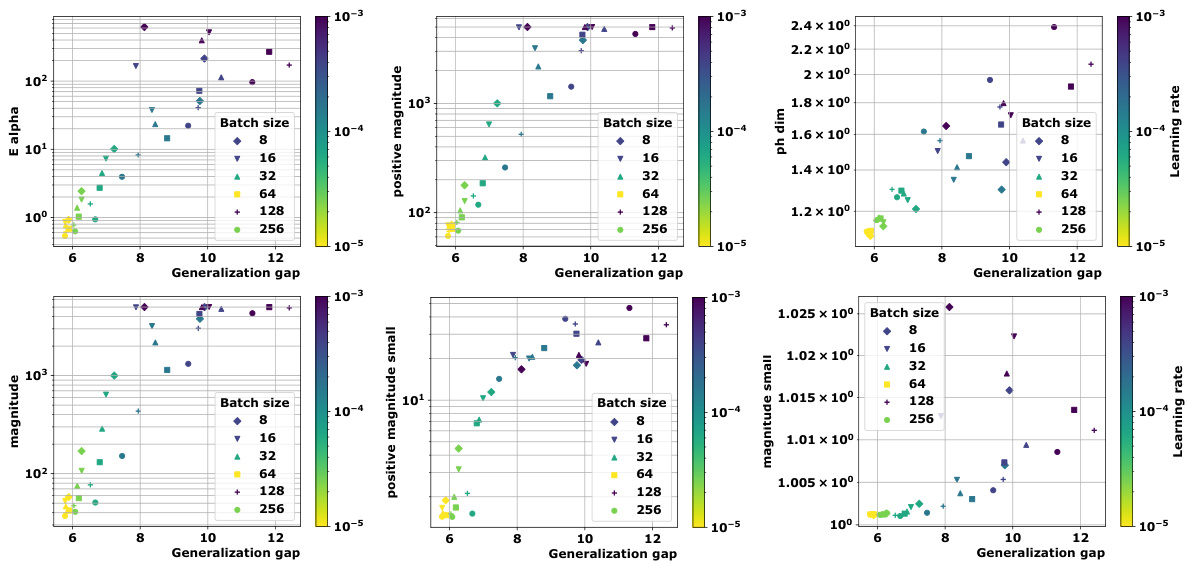
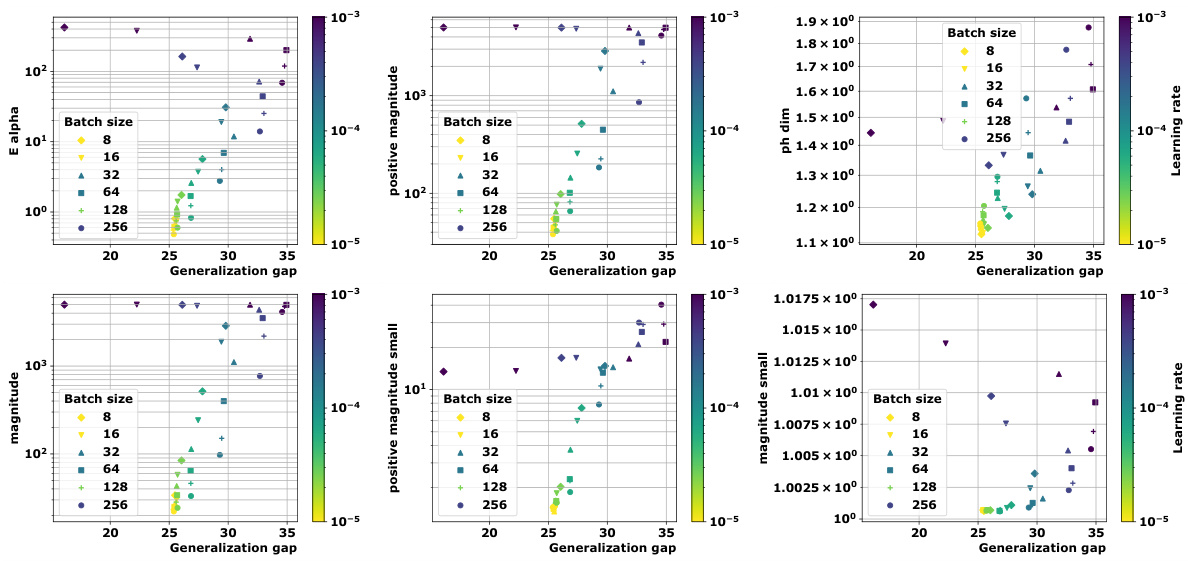
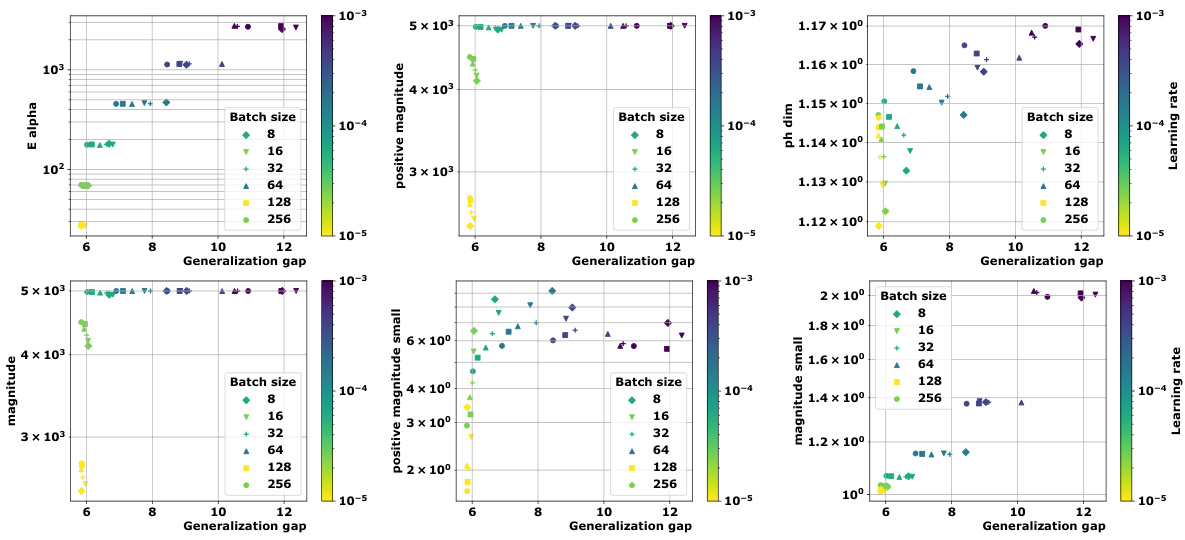
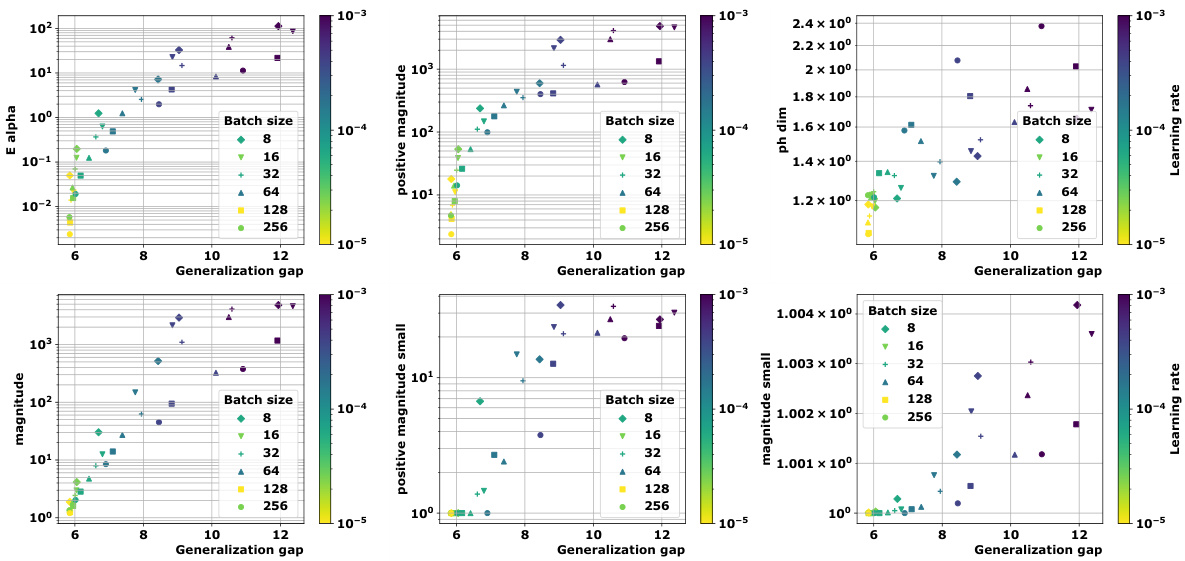
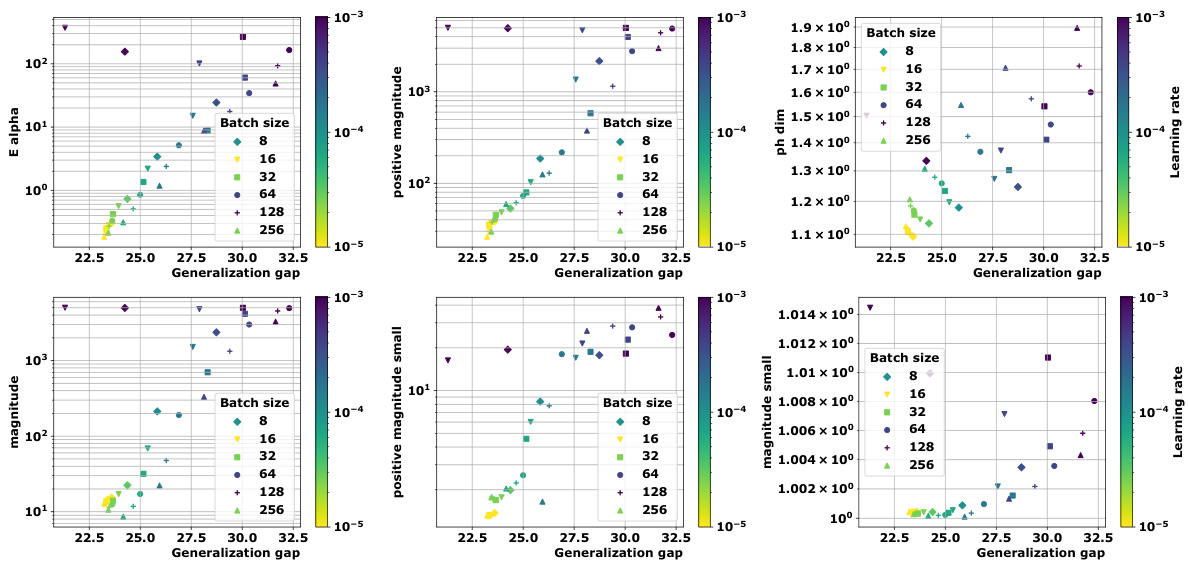
🔼 This table presents the correlation coefficients between different topological complexity measures and the generalization gap, calculated using the granulated Kendall’s tau coefficient. The results are shown for various models (vision transformers and graph neural networks) and datasets, across three different distance metrics: the data-dependent pseudometric (ps), the Euclidean distance (||.||2), and the 0-1 loss (01). The columns represent the correlation across all data, the correlation when only the learning rate is varied (LR), the correlation when only the batch size is varied (BS), and the average of LR and BS correlations (Ψ). The table aims to demonstrate the strong correlation between the proposed topological measures and the generalization gap, and their consistent outperformance compared to state-of-the-art persistent homology dimensions (dimpH).
read the caption
Table 1: Correlation coefficients associated with the different topological complexities.
In-depth insights#
Topological Bounds#
The concept of “Topological Bounds” in the context of a research paper likely refers to the use of topological concepts and tools to establish limits or constraints on certain quantities or phenomena. This approach moves beyond traditional, purely metric-based analyses, offering the potential for more robust and informative bounds, especially when dealing with complex, high-dimensional data or systems with intricate relationships. The power of topological methods lies in their ability to capture qualitative features and relationships that are not readily apparent in metric space. For instance, topological bounds might leverage concepts like persistent homology or the magnitude of a space to bound generalization error in machine learning. By considering the underlying structure and connectivity of data, these topological approaches can provide bounds that are more meaningful and resistant to noise or outliers. A key advantage is the potential for computationally efficient methods to estimate these topological quantities, even for high-dimensional data. However, the effectiveness of such methods is dependent on the appropriate choice of topological tools and metrics, as well as on assumptions about the data’s structure. A critical evaluation of these assumptions is essential to ensure the validity and reliability of the resulting bounds. Furthermore, a significant challenge lies in bridging the gap between the theoretical elegance of topological approaches and their practical applicability to real-world problems.
Discrete-Time TDA#
Discrete-Time TDA adapts topological data analysis (TDA) to the discrete-time nature of data generated by stochastic optimization algorithms used in training machine learning models. Traditional TDA often assumes continuous-time processes, which is unrealistic for iterative algorithms. This adaptation is crucial because it allows for the direct application of TDA techniques to actual training trajectories without needing approximations. This approach yields computationally efficient methods for generating topological complexity measures that strongly correlate with the generalization gap, providing rigorous generalization bounds for discrete-time algorithms. The shift to discrete-time TDA opens new avenues for analyzing learning dynamics and understanding the role of topology in generalization performance, leading to the development of more practical and reliable tools for model assessment and improvement.
Generalization Bounds#
The concept of ‘Generalization Bounds’ in machine learning is crucial for understanding a model’s ability to generalize to unseen data. Tight generalization bounds are highly desirable as they provide strong guarantees on the model’s performance. The paper likely explores various techniques for deriving these bounds, potentially leveraging topological data analysis (TDA) to capture the complexity of the model’s learning trajectory. This approach differs from traditional statistical learning theory, which often relies on simpler assumptions about the data distribution and model structure. TDA’s strength lies in its ability to handle high-dimensional, complex data often associated with deep neural networks. The paper’s contribution probably involves deriving novel bounds that are both theoretically sound and computationally tractable. This might involve introducing new complexity measures that accurately reflect the model’s generalization capabilities, potentially outperforming existing methods. A key aspect to consider would be how these new bounds relate to the discrete-time nature of training processes, as many existing bounds rely on continuous-time assumptions. The practicality and empirical validation of the proposed bounds through experiments on standard architectures and datasets are vital to demonstrate their effectiveness and potential impact on the field.
Empirical Analysis#
An Empirical Analysis section in a research paper would typically detail the experimental setup, data used, and the results obtained. It should clearly articulate how the experiments were designed to test the paper’s hypotheses. Specific details about models (architectures, hyperparameters), datasets, evaluation metrics, and the specific methods used to compute them are crucial. A strong empirical analysis presents results rigorously, typically including statistical significance tests (e.g., p-values, confidence intervals), to determine whether the observed effects are likely due to chance. Visualizations (plots, charts) are common and often help in conveying the findings effectively. Crucially, this section should discuss any limitations or unexpected outcomes. A thoughtful analysis will also place the findings in context with existing literature, drawing comparisons and offering potential explanations for any discrepancies. Reproducibility is key; the description of the experimental setup should be sufficiently detailed that other researchers can replicate the results. Finally, this section should directly address the original claims made in the introduction, summarizing how the experimental results support (or contradict) these claims. Overall, the success of a research paper frequently hinges on a robust, thorough, and well-presented empirical analysis.
Future Directions#
The paper’s core contribution is establishing novel topological complexity measures for evaluating generalization in deep learning models. Future directions should prioritize extending these measures to more complex architectures such as large language models and exploring their application in different domains beyond vision and graph neural networks. Further theoretical work is needed to reduce the reliance on information-theoretic terms in the generalization bounds, potentially by leveraging tighter concentration inequalities or refining existing assumptions. A deeper investigation into the practical implications of the proposed complexity measures is also vital. This includes examining the relationship between complexity and various hyperparameters (e.g., learning rate, batch size, optimizer selection) and studying the stability of the measures across different training runs and data subsets. Finally, exploring the use of topological complexity as a guide for algorithm design could lead to new training strategies aimed at improving the generalization performance of deep learning models.
More visual insights#
More on figures
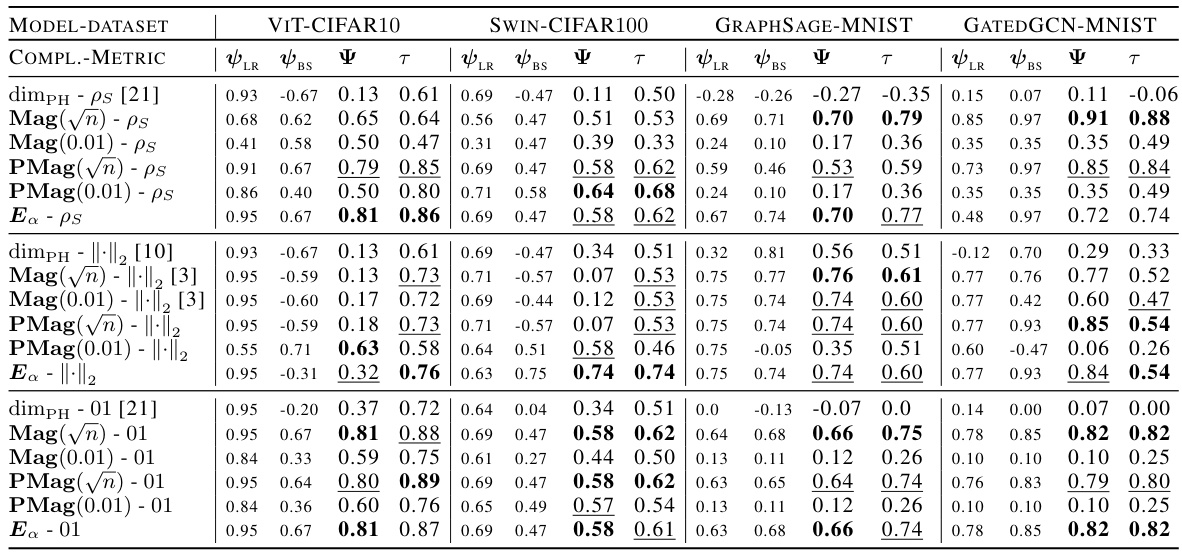
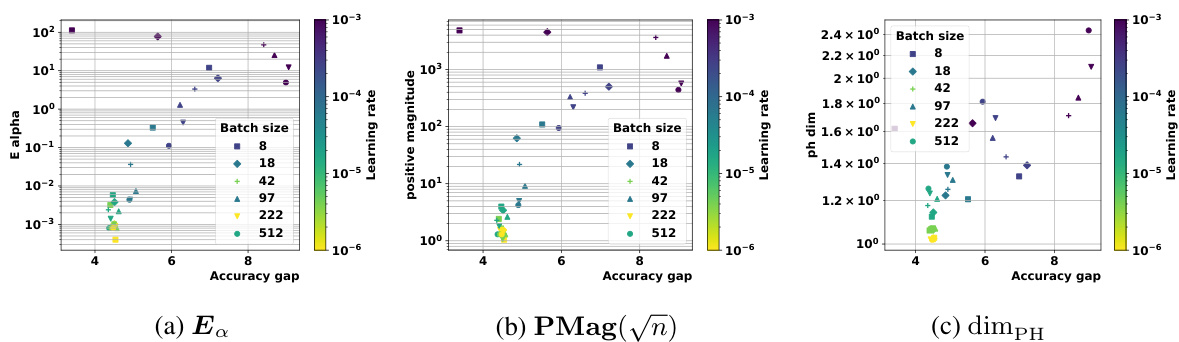
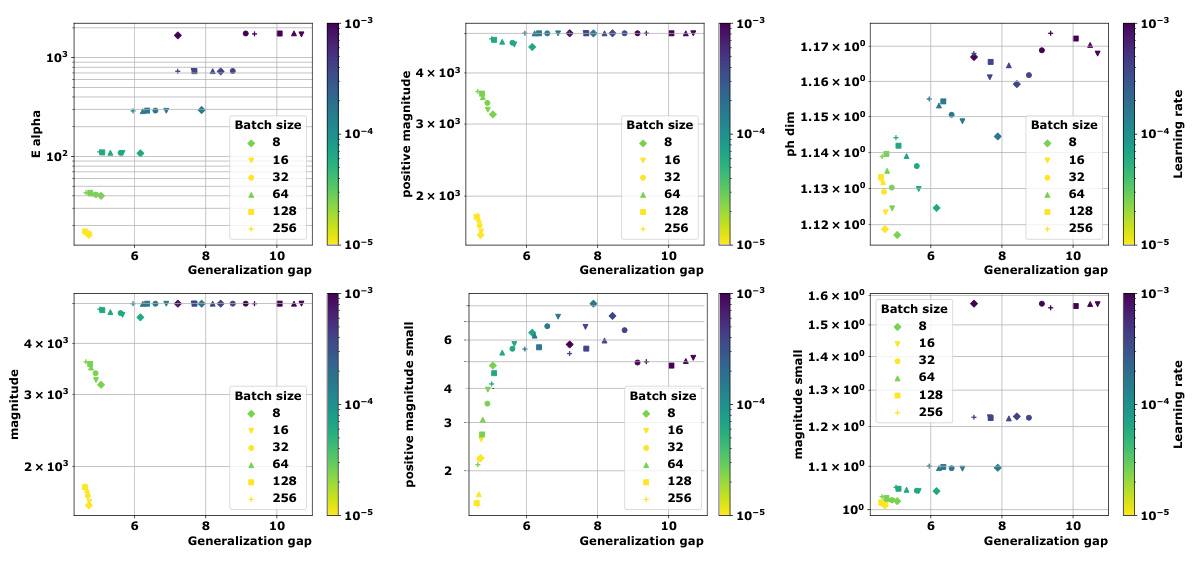
🔼 This figure compares the magnitude and positive magnitude measures for different (pseudo)metrics, namely the Euclidean distance, the ℓ¹-pseudometric ρs, and the 0-1 loss distance. The left panel shows the relationship between Mag and PMag, illustrating their close correlation for different metrics. The right panel shows how much the values of Ea and Mag vary when different proportions of the data are used to compute the pseudometric ρs. This demonstrates the robustness of these quantities to data subsampling.
read the caption
Figure 2: Left: Comparison of Mag and PMag (for s = √n), for different (pseudo)metrics (ViT on CIFAR10). Right: relative variation of the quantities Ea(Wto→T) and Mag(√nWto→T), with respect to the proportion of the data used to estimated ρs (ViT on CIFAR10).
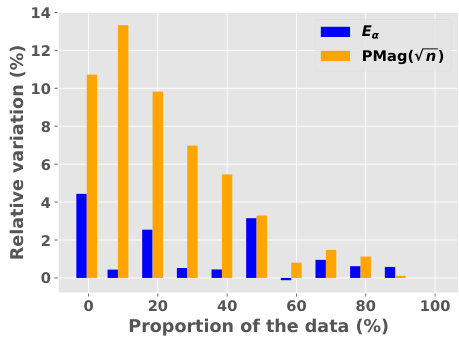
🔼 This figure compares the magnitude (Mag) and positive magnitude (PMag) for different metrics, showing a strong correlation between them. The left panel shows a scatter plot of Mag vs. PMag, demonstrating their close relationship. The right panel shows the relative variation of Ea and Mag with respect to the proportion of data used in calculating the pseudometric, highlighting the robustness of these measures.
read the caption
Figure 2: Left: Comparison of Mag and PMag (for s = √n), for different (pseudo)metrics (ViT on CIFAR10). Right: relative variation of the quantities Ea(Wto→T) and Mag(√nWto→T), with respect to the proportion of the data used to estimated p) (ViT on CIFAR10).
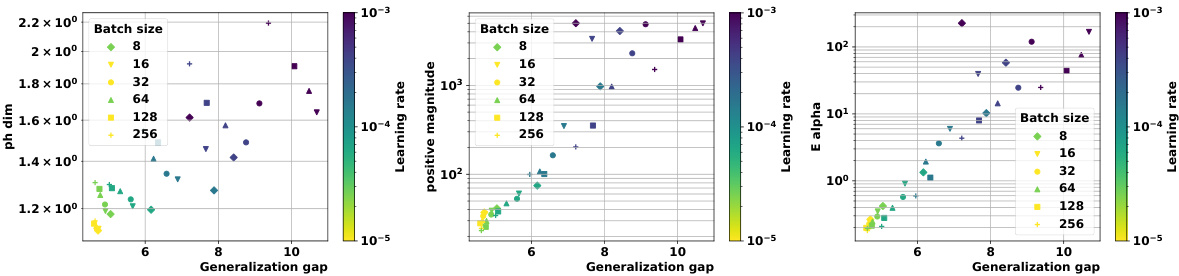
🔼 This figure demonstrates the correlation between topological properties of training trajectories and generalization performance. It shows three subfigures: (a) Multi-dimensional scaling (MDS) trajectory embeddings based on different distance metrics, (b) Distance matrices of the trajectories, and (c) A comparison of proposed generalization measures and state-of-the-art methods, highlighting the significant gains and practical relevance of the proposed measures.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure shows the topological properties of discrete training trajectories of several deep networks. The subfigures (a) and (b) display the trajectories embedded with multi-dimensional scaling based on different distance matrices, using either the Euclidean distance or the loss-induced pseudo-metric. Subfigure (c) shows the average granulated Kendall coefficients, comparing the proposed generalization measures (Ea and PMag(n)) with the state-of-the-art persistent homology dimensions on different models, datasets and domains.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
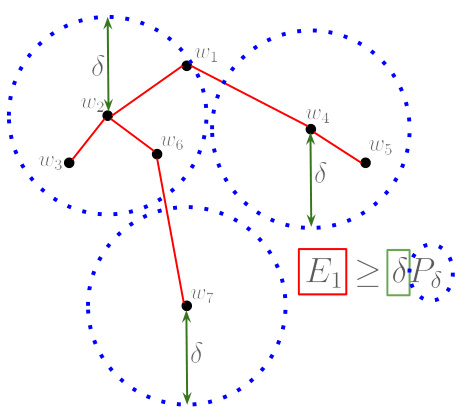
🔼 This figure provides a geometric illustration of Lemma B.12, which is a crucial step in proving the persistent homology bounds. It depicts a point cloud representing a finite pseudometric space, with points colored black and labeled w1 through w7. The points are arranged and connected by lines in a tree-like structure to represent a minimum spanning tree (MST) which contains the edges needed to compute Ea. Three groups of points surrounded by blue dotted circles illustrate the concept of a maximal 8-packing, in which points within each circle are a distance 8 apart from each other. The red square and green rectangle illustrate that the cost of MST, Ea, is greater than or equal to the size of the maximal 8-packing. The figure visually demonstrates the relationship between the MST structure, the packing, and the persistent homology dimension.
read the caption
Figure 5: Geometric representation of the proof of Lemma B.12. It represents a point cloud (wi)i, the centers of the 3 packing balls (blue) and the minimum spanning tree T (red), so that the sum of the lengths of the edges of T is exactly E1, see Appendix A.
🔼 This figure demonstrates the topological complexity measures developed in the paper. Subfigure (a) shows multidimensional scaling (MDS) trajectory embeddings for various deep learning models trained on different datasets. Subfigure (b) presents distance matrices of these trajectories, computed using both Euclidean distance and a loss-induced pseudo-metric. Subfigure (c) displays a comparison of the average granulated Kendall’s tau coefficients between two proposed measures (Ea and PMag(n)) and existing persistent homology dimensions. The high correlation shown indicates that these new topological measures effectively capture generalization properties.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the effectiveness of the proposed topological complexity measures in capturing the generalization ability of different deep learning models. It shows how these measures correlate with test performance across various model architectures, datasets, and data domains. The figure displays multi-dimensional scaling embeddings of training trajectories, distance matrices calculated using different metrics, and finally, a comparison of the proposed measures to the state-of-the-art, revealing their superior performance and practical relevance.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure demonstrates the correlation between topological properties of training trajectories and generalization performance. Subfigure (a) shows multi-dimensional scaling (MDS) embeddings of training trajectories for various models and datasets. Subfigure (b) displays distance matrices calculated using either Euclidean distance or loss-induced pseudo-metric. Subfigure (c) presents a comparison of proposed topological complexity measures (Ea and PMag(n)) with existing state-of-the-art persistent homology dimensions, using average granulated Kendall coefficients to show their correlation with generalization.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
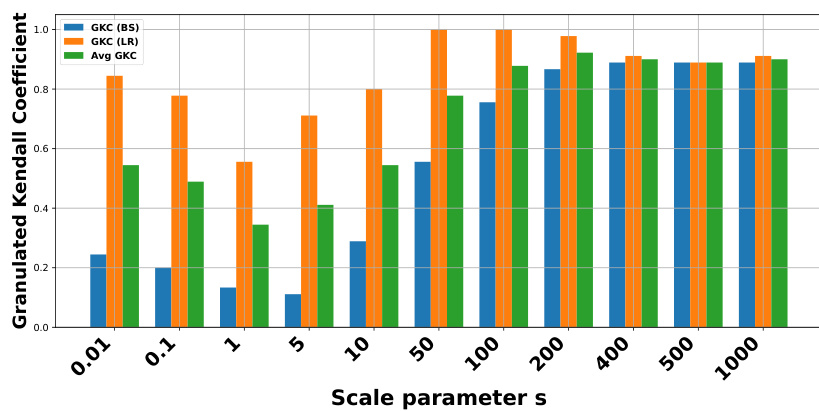
🔼 This figure shows the sensitivity analysis of the scale parameter ’s’ used in the positive magnitude calculation (PMag) on the generalization performance. The experiment was conducted using a Vision Transformer (ViT) model trained on the CIFAR10 dataset with the ADAM optimizer. The x-axis represents different values of the scale parameter ’s’, and the y-axis shows the average granulated Kendall’s coefficient (Avg GKC), a measure of correlation between the topological complexity (PMag) and the generalization error. The plot aims to determine how stable the correlation is across various values of ’s’ showing a relative stability, especially for higher ’s’ values.
read the caption
Figure 9: Sensitivity analysis of the scale parameter s for positive magnitude PMag(sWto→T). Experiment made with ViT on CIFAR10 and ADAM optimizer.

🔼 This figure shows the topological properties of discrete training trajectories and how they correlate with generalization performance. Panel (a) displays multi-dimensional scaling embeddings of training trajectories for different models and datasets. Panel (b) shows distance matrices calculated using Euclidean distance and a loss-induced pseudo-metric. Panel (c) compares average granulated Kendall coefficients of the proposed generalization measures (Ea and PMag(n)) against state-of-the-art methods based on persistent homology, demonstrating the superiority of the proposed measures across different model architectures, datasets and optimization algorithms.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the strong correlation between topological complexity measures and generalization performance in deep neural networks. Panel (a) shows multi-dimensional scaling embeddings of training trajectories from different models and datasets. Panel (b) displays distance matrices calculated using either Euclidean distance or a loss-induced pseudo-metric. Panel (c) presents average granulated Kendall coefficients for two novel topological complexity measures, compared to existing state-of-the-art measures, highlighting a stronger correlation with the generalization gap.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure demonstrates the correlation between topological properties of training trajectories and generalization performance in deep neural networks. Panel (a) shows multi-dimensional scaling embeddings of training trajectories for various models and datasets. Panel (b) illustrates the distance matrices calculated using either Euclidean distance or a loss-induced pseudo-metric. Panel (c) presents the average granulated Kendall coefficients (a measure of correlation) for two new topological complexity measures (‘Ea’ and ‘PMag(n)’) compared to state-of-the-art persistent homology dimensions, highlighting the strong correlation between topological complexity and generalization error.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure demonstrates the effectiveness of the proposed topological complexity measures in predicting generalization performance. It shows that the topological properties of discrete training trajectories, captured by the new measures, strongly correlate with generalization error across various deep learning models, datasets, and optimizers. Subfigure (a) displays multi-dimensional scaling (MDS) embeddings of training trajectories, while (b) shows distance matrices calculated using both Euclidean distance and a loss-induced pseudo-metric. Subfigure (c) compares the average granulated Kendall’s tau coefficients for the novel topological measures against state-of-the-art persistent homology dimensions, highlighting the superior performance of the proposed methods.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the topological complexity measures introduced in the paper. Subfigure (a) shows multi-dimensional scaling (MDS) embeddings of training trajectories for various models and datasets. Subfigure (b) displays distance matrices calculated using Euclidean distance and a loss-induced pseudo-metric. Finally, subfigure (c) compares the average granulated Kendall’s Tau correlation coefficients between the proposed topological complexity measures and state-of-the-art measures. It highlights that the new measures highly correlate with generalization error.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure visualizes the topological properties of training trajectories and how they relate to generalization. It shows trajectories embedded using multi-dimensional scaling, distance matrices computed using Euclidean distance and loss-induced pseudo-metric, and average granulated Kendall coefficients for two generalization measures. The results highlight a strong correlation between topological complexity and generalization performance across various models and datasets.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure demonstrates the proposed topological complexity measures for generalization. It shows training trajectories embedded using multi-dimensional scaling (MDS). Different distance metrics (Euclidean and loss-induced) are compared for computing distance matrices. Finally, the average granulated Kendall coefficients for the new measures (Ea and PMag(n)) are plotted against state-of-the-art persistent homology dimensions, highlighting their superior correlation with generalization performance across various models, datasets, and domains.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure shows the topological properties of discrete training trajectories and their correlation with generalization performance. Panel (a) displays multi-dimensional scaling (MDS) trajectory embeddings using two different distance metrics. Panel (b) shows distance matrices of trajectories, again using two different distance metrics. Panel (c) compares the average granulated Kendall coefficients for two proposed generalization measures (Ea and PMag(n)) against state-of-the-art persistent homology dimensions (PH-dim), demonstrating the effectiveness of the proposed methods.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the topological complexity measures proposed in the paper. Subfigure (a) shows multi-dimensional scaling (MDS) embeddings of training trajectories for several different models and datasets. Subfigure (b) shows distance matrices calculated using both Euclidean distance and a loss-induced pseudo-metric. Subfigure (c) shows a comparison of the average granulated Kendall coefficients between the new measures (Ea and PMag(n)), and state-of-the-art persistent homology dimensions, highlighting the superior performance and practical relevance of the new measures.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the correlation between topological properties of training trajectories and generalization performance. Subfigure (a) shows multi-dimensional scaling embeddings of the training trajectories for various models and datasets, using two different distance measures. (b) Displays the distance matrices used for those embeddings. Finally, (c) compares the average granulated Kendall coefficients for two proposed topological complexity measures (‘Ea’ and ‘PMag(n)’) against existing state-of-the-art measures based on persistent homology, showing significantly improved correlation with generalization performance.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure demonstrates the correlation between topological properties of training trajectories and generalization performance in deep neural networks. It shows how multi-dimensional scaling (MDS) can embed training trajectories based on different distance metrics (Euclidean and loss-induced). The key finding is that the proposed topological measures (Ea and PMag(n)) correlate highly with generalization error, outperforming existing methods based on persistent homology dimensions.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the correlation between topological properties of training trajectories and generalization performance in deep neural networks. It shows how three different visualization methods (MDS embeddings, distance matrices, and topological complexity measures) highlight the relationship between the topology of training trajectories and generalization error. The use of both Euclidean and loss-induced distances enhances the understanding of how different distance metrics influence the outcome. The high correlation between the newly proposed topological complexity measures and generalization error validates their effectiveness.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the correlation between topological properties of discrete training trajectories and generalization performance in deep neural networks. Panel (a) shows multi-dimensional scaling (MDS) embeddings of training trajectories, visualizing the weights of neural networks over training iterations. The distance matrices in (b) are calculated using either the Euclidean distance or a loss-induced pseudo-metric. Panel (c) presents average granulated Kendall coefficients showing the strong correlation between proposed topological complexity measures and generalization error, outperforming existing methods. Different models, datasets, and optimizers are used to highlight the generality and effectiveness of the proposed measures.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the topological complexity measures proposed in the paper. It shows how the topological properties of discrete training trajectories correlate with test performance. The subfigures show (a) MDS trajectory embeddings, (b) distance matrices of trajectories, and (c) topological generalization measures. The figure shows that the proposed methods outperform existing methods across various datasets, models, and optimizers.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure shows the topological analysis of discrete training trajectories for various deep learning models. Panel (a) displays multidimensional scaling (MDS) embeddings of the trajectories. Panel (b) shows distance matrices, calculated using Euclidean distance and a loss-induced pseudo-metric. Panel (c) presents a comparison of the average granulated Kendall’s coefficient for two new topological complexity measures (Ea and PMag(n)) against existing persistent homology dimension measures. The results demonstrate a strong correlation between these new measures and generalization performance, suggesting their value for predicting generalization.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure shows the topological properties of discrete training trajectories for various deep learning models. Panel (a) displays multi-dimensional scaling (MDS) embeddings of these trajectories. Panel (b) shows the distance matrices used to create these embeddings, comparing Euclidean distance and a loss-induced pseudo-metric. Panel (c) presents a comparison of the authors’ new topological complexity measures with state-of-the-art methods, showing the correlation between these measures and generalization performance.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
🔼 This figure shows how new topological complexity measures correlate with generalization performance across various deep learning models and datasets. Panel (a) displays multi-dimensional scaling (MDS) embeddings of training trajectories. Panel (b) shows distance matrices for these trajectories, calculated using both Euclidean distance and a loss-induced pseudo-metric. Panel (c) compares average granulated Kendall’s tau coefficients for two proposed measures against state-of-the-art methods, highlighting superior performance and practical relevance.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
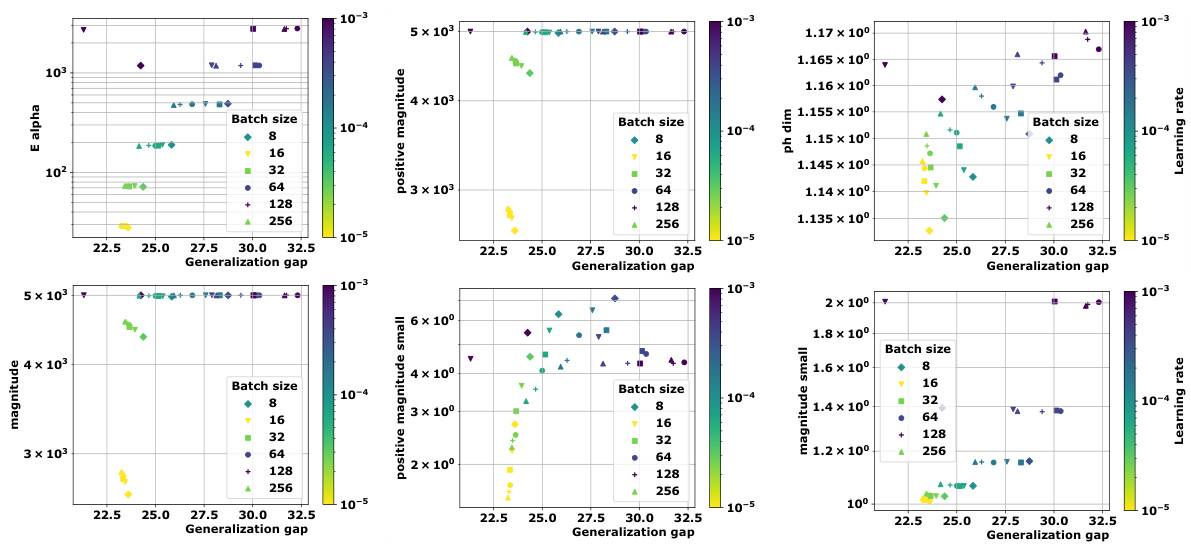
🔼 This figure demonstrates the strong correlation between the topological properties of discrete training trajectories and generalization performance in deep neural networks. Panel (a) shows trajectory embeddings using multidimensional scaling. Panel (b) displays distance matrices calculated using Euclidean distance and a loss-induced pseudometric. Panel (c) compares the average granulated Kendall coefficients of two new topological complexity measures (Ea and PMag(n)) against state-of-the-art persistent homology dimensions, highlighting the superior performance of the proposed measures across various models and datasets.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
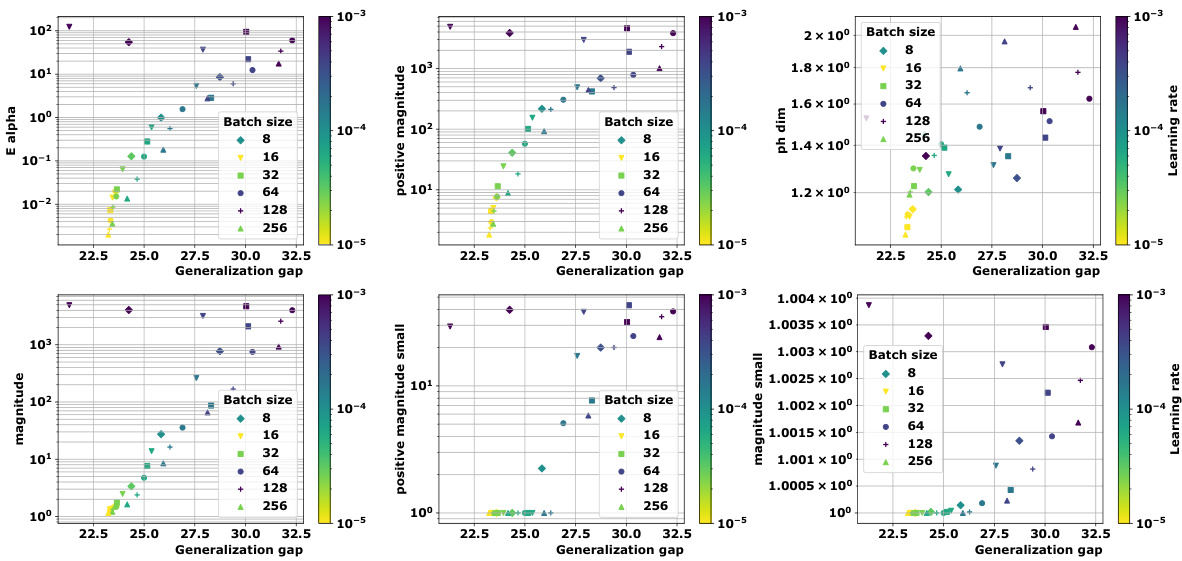
🔼 This figure visualizes the topological complexity measures proposed in the paper. Subfigure (a) shows multi-dimensional scaling (MDS) embeddings of training trajectories for various models and datasets. Subfigure (b) presents distance matrices calculated using both Euclidean distance and a loss-induced pseudo-metric. Finally, subfigure (c) compares the average granulated Kendall correlation coefficients for two proposed topological measures with existing methods (persistent homology dimensions), demonstrating their superior correlation with generalization error.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
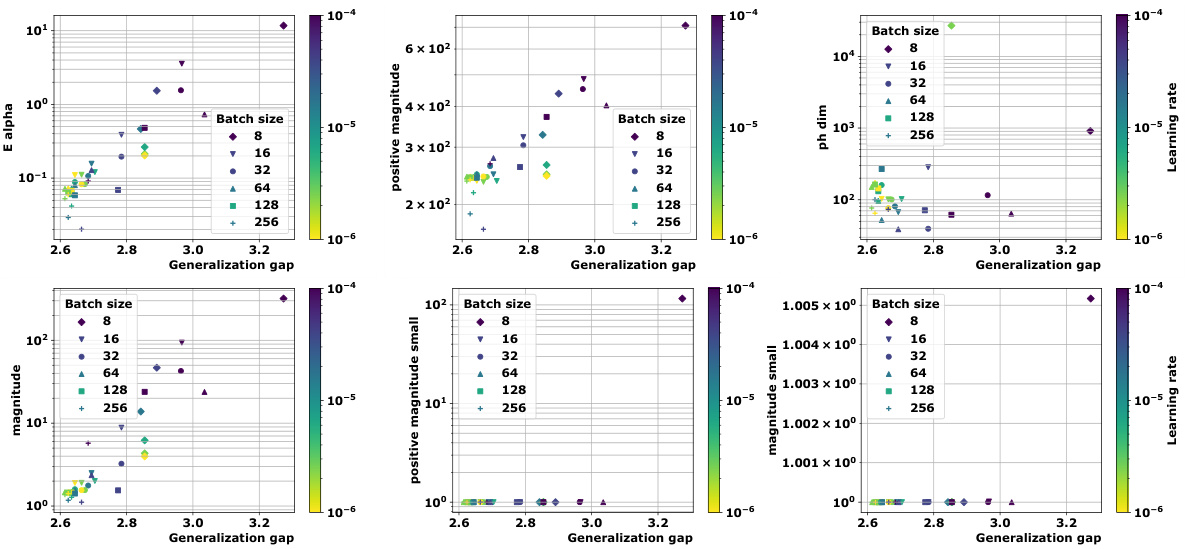
🔼 This figure demonstrates the novel topological complexity measures proposed in the paper. Subfigure (a) shows multi-dimensional scaling (MDS) embeddings of training trajectories for various models and datasets. Subfigure (b) displays distance matrices calculated using Euclidean distance and a loss-induced pseudo-metric. Finally, subfigure (c) presents average granulated Kendall coefficients comparing the proposed measures (Ea and PMag(n)) against existing persistent homology dimensions, showcasing improved correlation with generalization.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the correlation between topological properties of training trajectories and generalization performance in deep neural networks. Panel (a) shows trajectory embeddings using multidimensional scaling. Panel (b) displays distance matrices calculated using Euclidean distance and a loss-induced pseudo-metric. Panel (c) compares average granulated Kendall coefficients for new topological complexity measures (Ea and PMag(n)) with state-of-the-art persistent homology dimensions, highlighting superior correlation with generalization error.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the strong correlation between topological complexity measures and generalization performance in deep neural networks. It shows how the topological properties of training trajectories (embedded using multi-dimensional scaling) correlate with generalization error, as measured by the average granulated Kendall coefficient. The figure compares the performance of two new topological measures (Ea and PMag(n)) against existing state-of-the-art methods, highlighting the improved performance and practical relevance of the proposed measures.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the proposed topological complexity measures and their correlation with generalization performance. Panel (a) shows multi-dimensional scaling embeddings of training trajectories from different models and datasets. Panel (b) illustrates the distance matrices used in the embeddings, comparing Euclidean distance with a loss-induced pseudometric. Panel (c) presents the average granulated Kendall coefficients showing that the new topological measures (Ea and PMag(n)) provide a significantly stronger correlation with generalization performance than state-of-the-art persistent homology dimensions.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the correlation between topological properties of training trajectories and generalization performance in deep neural networks. It shows three subfigures: (a) Multidimensional scaling (MDS) embeddings of training trajectories for various models and datasets; (b) Distance matrices calculated using either Euclidean distance or a loss-induced pseudo-metric, visualizing the trajectories’ proximity; (c) Average granulated Kendall coefficients comparing the authors’ proposed topological generalization measures (Ea and PMag(n)) against existing persistent homology dimensions. The results highlight a strong correlation between the proposed measures and generalization, showcasing their effectiveness in predicting test performance without needing test data.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.

🔼 This figure demonstrates the strong correlation between topological complexity measures and generalization performance. Subfigure (a) shows multi-dimensional scaling embeddings of training trajectories, calculated using different distance metrics. Subfigure (b) displays distance matrices for these trajectories, highlighting differences based on metric choice. Finally, subfigure (c) presents a comparison of the average granulated Kendall coefficients for the proposed topological measures (Ea and PMag(n)) against existing persistent homology dimension methods. The results indicate that the novel measures correlate highly with generalization error and are more efficient than the state-of-the-art.
read the caption
Figure 1: We devise a novel class of complexity measures that capture the topological properties of discrete training trajectories. These generalization bounds correlate highly with the test performance for a variety of deep networks, data domains and datasets. Figure shows different trajectories (a) embedded using multi-dimensional scaling based on the distance-matrices (b) computed using either the Euclidean distance (||. ||2) between weights as in [10] or via the loss-induced pseudo-metric (ps) as in [21]. (c) plots the average granulated Kendall coefficients for two of our generalization measures (Ea and PMag(n)) in comparison to the state-of-the-art persistent homology dimensions [10, 21] for a range of models, datasets, and domains, revealing significant gains and practical relevance.
More on tables

🔼 This table presents the architecture details for the vision transformers used in the experiments. The details include the model name, dataset used, depth, patch size, token dimension, number of heads, MLP ratio, window size, and the total number of parameters for each model. This information is crucial for understanding the computational complexity and scale of the models used in the research. The models listed are ViT, Swin, and CaiT, all tested on CIFAR10 and CIFAR100 datasets.
read the caption
Table 2: Architecture details for the vision transformers (taken from [29]). WS refers to Window Size.
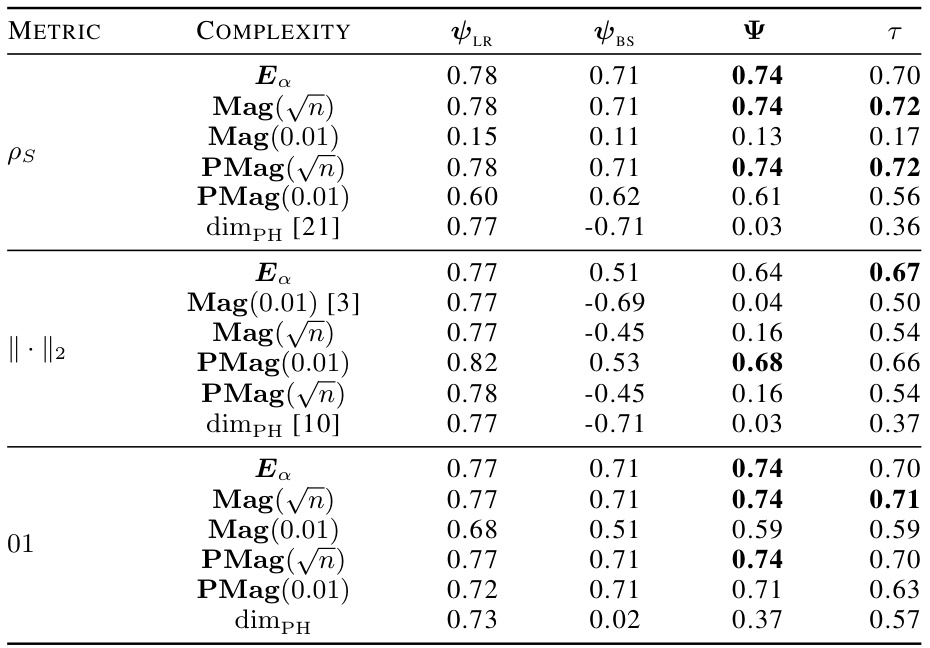
🔼 This table presents the correlation coefficients between different topological complexity measures and the generalization error for various deep learning models and datasets. The correlation is measured using Granulated Kendall’s coefficient (GKC) which considers the correlation of topological complexity measure with generalization gap when only one hyperparameter is changing. The table includes three different pseudometrics used to compute distance matrices. The table helps to quantify the relationship between topological complexity and generalization performance across different deep learning models and datasets, providing a comparative evaluation of different topological measures.
read the caption
Table 1: Correlation coefficients associated with the different topological complexities.

🔼 This table presents the correlation coefficients between several topological complexity measures and the generalization error. It shows the correlation for different models (Vision Transformers and Graph Neural Networks), datasets (CIFAR10, CIFAR100, MNIST), and distance metrics (Euclidean distance, data-dependent pseudometrics based on loss). The correlations are assessed using the granulated Kendall’s coefficient (GKC) considering learning rates and batch sizes. The table helps in comparing the effectiveness of different topological measures in predicting generalization.
read the caption
Table 1: Correlation coefficients associated with the different topological complexities.

🔼 This table presents the correlation coefficients between different topological complexity measures and the generalization error for various deep learning models trained on different datasets. The correlation is calculated using the granulated Kendall’s coefficient, which accounts for correlation when only a single hyperparameter changes, as well as the traditional Kendall’s coefficient (τ). The table includes results for several models (ViT, Swin, GraphSage, GatedGCN), datasets (CIFAR10, CIFAR100, MNIST), and distance metrics (ps, Euclidean, 01 loss). It facilitates comparison of the effectiveness of various topological measures, including the persistent homology dimension and our proposed measures (Ea, Mag, PMag).
read the caption
Table 1: Correlation coefficients associated with the different topological complexities.

🔼 This table presents the correlation coefficients between various topological complexity measures (Ea, Mag(n), Mag(0.01), PMag(n), PMag(0.01), dimPH) and the generalization gap for different models (ViT, Swin, GraphSage, GatedGCN) and datasets (CIFAR10, CIFAR100, MNIST). Each topological measure is computed using different distance metrics (ps, ||.||2, 01). The table shows the Kendall’s correlation coefficients (τ, ψLR, ψBS, ψ) which measure the correlation between the topological complexities and the generalization gap for different hyperparameters (learning rate, batch size).
read the caption
Table 1: Correlation coefficients associated with the different topological complexities.

🔼 This table presents the correlation coefficients between different topological complexity measures (Ea, Mag(n), Mag(0.01), PMag(n), PMag(0.01), and dimPH) and the generalization error (Gs) for various models (ViT, Swin, GraphSage, GatedGCN) and datasets (CIFAR10, CIFAR100, MNIST). Different distance metrics (ps, ||.||2, 01) are used for computing the topological complexities. The table also shows the granulated Kendall’s coefficients (τ, ψLR, ψBS, ψ) for each measure, providing a more nuanced understanding of the correlation strength based on the variation of learning rate and batch size.
read the caption
Table 1: Correlation coefficients associated with the different topological complexities.
Full paper#