TL;DR#
Reinforcement learning (RL) often faces challenges with incomplete information and changing environments. Low-rank Markov Decision Processes (MDPs) provide a simplified yet expressive model, but existing research struggles when both transition probabilities are unknown and the learner only receives feedback on selected actions (bandit feedback). Adding to the difficulty, this paper considers an adversarial setting where rewards can change arbitrarily.
This research directly addresses these challenges. The authors present novel model-based and model-free algorithms that significantly improve upon existing regret bounds (the measure of algorithm performance) for both full-information and bandit feedback scenarios in adversarial low-rank MDPs. They demonstrate their algorithms’ effectiveness and provide a theoretical lower bound, highlighting when high regret is unavoidable.
Key Takeaways#
Why does it matter?#
This paper is crucial for reinforcement learning researchers as it tackles the challenging problem of adversarial low-rank Markov Decision Processes (MDPs) with unknown transitions and bandit feedback. It offers novel model-based and model-free algorithms, achieving improved regret bounds. This research directly addresses current limitations in handling uncertainty and partial information in RL, pushing the boundaries of theoretical understanding and practical applicability.
Visual Insights#
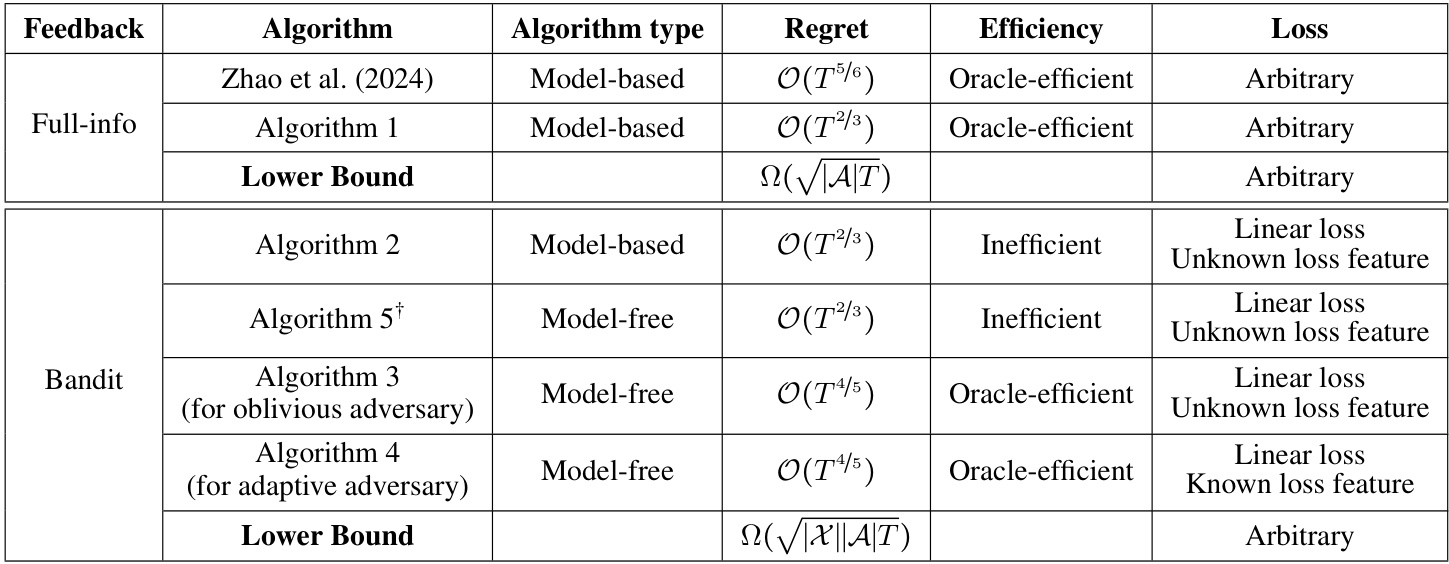
🔼 This table compares different algorithms for solving adversarial low-rank Markov Decision Processes (MDPs) problems. It categorizes them based on the type of feedback (full information or bandit), algorithm type (model-based or model-free), regret bound achieved, efficiency (oracle-efficient or inefficient), and the type of loss function considered. The table highlights the trade-offs between these aspects for different approaches. Note that ‘O’ represents factors of order poly(d, |A|, log T, log |Φ||Y|).
read the caption
Table 1: Comparison of adversarial low-rank MDP algorithms. O here hides factors of order poly (d, |A|, log T, log|Φ||Y|). *Algorithm 5 assumes access to p(x, a) for any (φ, x, α) є Ф × X × A, while other algorithms only require access to f(x, a) for any (φ, α) є Ф × A on visited x.
Full paper#



















