TL;DR#
Prior models for neural network gradients have been largely unexplored due to their high dimensionality and complexity. This necessitates efficient gradient compression methods, especially in distributed learning, to mitigate communication bottlenecks. Lossy compression sacrifices precision, while lossless methods lack effective statistical models for gradients.
This research introduces LM-GC, a novel method leveraging large language models (LLMs) to act as gradient priors for arithmetic coding. LM-GC converts gradients into text-like formats, enabling LLMs to estimate probabilities for arithmetic encoding, achieving higher compression rates than state-of-the-art baselines. Experiments show significant improvements in compression ratios (10% to 17.2%) across various datasets and architectures, highlighting the potential of using LLMs for lossless gradient compression and its compatibility with lossy techniques.
Key Takeaways#
Why does it matter?#
This paper is highly relevant to researchers working on federated learning, distributed optimization, and gradient compression techniques. It introduces a novel approach using LLMs, opening new avenues for improving efficiency in large-scale machine learning. By demonstrating the efficacy of lossless gradient compression using LLMs, this paper contributes significantly to the development of more efficient and scalable machine learning systems.
Visual Insights#
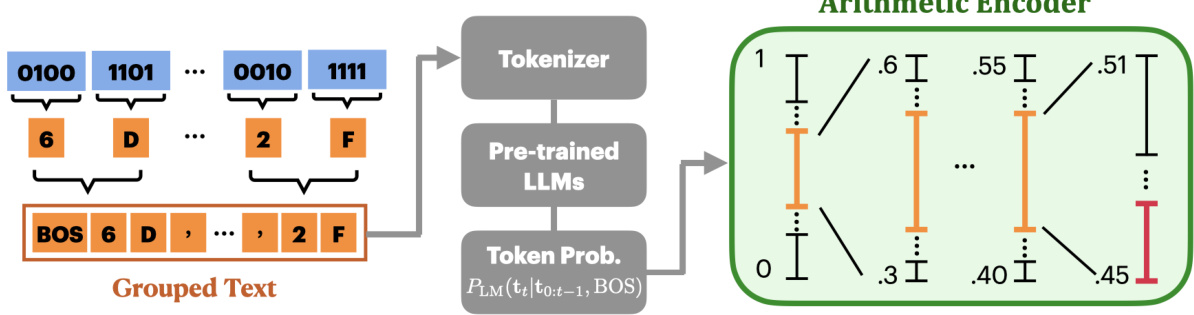
🔼 This figure illustrates the LM-GC (Language Model Gradient Compression) method. It shows how raw gradient data (represented as bits) is converted into a text-like format using hexadecimal numbers and separators. This textual representation is then fed into a pre-trained Language Model (LLM) to predict the probability of each token. Finally, arithmetic encoding uses these probabilities to compress the gradient data. The diagram also visually explains the basic principle of arithmetic encoding.
read the caption
Figure 1: Overview of LM-GC. Our method initially converts every 4 bits into hexadecimal numbers and groups them with separators in between, e.g., commas in the figure. The grouped text is then input to a pre-trained, frozen tokenizer and LLM to produce the probability of each token. These probabilities are used for arithmetic encoding, where a line segment between 0 and 1 is repeatedly split according to the token probability until reaching a predefined maximum length. Any number from that region (e.g., the midpoint) can accurately represent the original data. We provide an example of how arithmetic coding works in Sec. 3.

🔼 This table compares the compression rates achieved by various lossless compression methods, including traditional codecs (PNG, FLAC, GZIP, LZMA, FPZIP) and the proposed LM-GC method using different LLMs (Tinyllama 1.1B, Openllama 3B, LLAMA 2 7B). The LM-GC method incorporates different serialization techniques to convert gradients into text-like formats, which are then processed by the LLMs for compression. The table highlights the impact of serialization on compression efficiency and demonstrates the superior performance of LM-GC compared to traditional codecs.
read the caption
Table 1: Gradient compression rate using PNG, FLAC, GZIP, LZMA, FPZIP, and our method with various language models. Our method considers different serializations including iso-8859-1 (ISO), hexadecimal numbers without separators (Hn) and with spaces (H5), commas (Hc), commas+spaces (Hc+s), and semicolons (Hsemi) to group every four bytes from the same floating point.
In-depth insights#
LLM Gradient Priors#
The concept of “LLM Gradient Priors” introduces a novel approach to leveraging the power of large language models (LLMs) in optimizing neural networks. Instead of traditional statistical methods, LLMs are proposed as a powerful prior model for representing the probability distribution of neural network gradients. This is a significant shift, as it bypasses the complexities of explicitly modeling high-dimensional gradient structures. The core idea is that LLMs, trained on massive text data, can implicitly learn to capture underlying patterns and relationships within gradient information. This capability can be harnessed for applications such as lossless gradient compression, where accurate probability modeling is crucial for achieving high compression ratios. Furthermore, the zero-shot nature of this approach is compelling, removing the need for extensive training data specific to gradients. However, the success heavily depends on the effective conversion of gradients into a format suitable for LLMs, a process that warrants further investigation. Ultimately, the potential of LLMs as gradient priors could fundamentally alter the landscape of neural network optimization, and opens new avenues for research into more efficient and effective training techniques.
LM-GC: Method#
The core of the LM-GC method lies in its innovative two-step process: serialization and compression. Serialization cleverly transforms raw gradient data, typically represented as 32-bit floating-point numbers, into a text-like format more readily interpretable by Large Language Models (LLMs). This involves converting the raw bits into hexadecimal numbers and strategically inserting separators (spaces, commas, etc.) to enhance the structural clarity of the data for the LLM. This crucial step is key to the method’s effectiveness, significantly improving token efficiency compared to using plain gradient representations. The second step, compression, leverages the serialized text and the LLM to predict the probability of each token. These probabilities are then used in arithmetic coding, a highly effective lossless compression technique, to obtain a compact representation of the gradients. The zero-shot nature of the approach—using pre-trained LLMs without any fine-tuning on gradient data—is a significant advantage. The method’s success hinges on the ability of LLMs to accurately model the probability distribution of the serialized gradient data, demonstrating their potential as powerful, general-purpose prior models for gradients.
Compression Rates#
Analyzing compression rates in this context reveals significant improvements achieved by the proposed LM-GC method over traditional lossless compression techniques. The results demonstrate a substantial reduction in data size, ranging from 10% to 17.2% across various datasets and network architectures. This improvement is particularly notable when considering the complexity of gradient data, which often presents challenges for effective compression. The integration of LLMs with arithmetic coding is key to LM-GC’s success, as LLMs effectively model the probability distribution of gradient data, leading to higher compression efficiency. The choice of serialization technique, including the use of separators and the optimal grouping of bytes, also significantly affects the final compression ratio, highlighting the importance of data formatting for efficient LLM processing. Further research should explore the impact of various LLM architectures and sizes on compression rates, seeking to optimize performance and resource utilization. Ultimately, robustness and generalizability are important indicators of the method’s true potential and the level of improvement that might be expected in broader applications.
Ablation Studies#
Ablation studies systematically remove components of a model to understand their individual contributions. In this context, it is likely that ablation studies were performed to assess the impact of different elements within the gradient compression framework. The choice of LLM, the tokenization strategy (including the use of separators), and the various serialization techniques are prime candidates for ablation. By selectively removing each component and measuring the impact on the compression ratio, researchers could quantify the contribution of each feature and identify areas for potential improvement or simplification. For instance, removing separators might show a significant decrease in compression effectiveness, highlighting their crucial role in facilitating LLM comprehension. These results would justify design decisions and provide valuable insights into the key factors driving performance. Furthermore, ablation could explore the influence of context window size in the LLMs, demonstrating how much contextual information is truly necessary for effective probability modeling. The interplay between different components and potential redundancies are also likely investigated. Ultimately, ablation studies offer a crucial validation strategy, clarifying the architecture’s key mechanisms and potentially optimizing for greater efficiency and robustness.
Future Work#
Future research directions stemming from this work could explore extending LM-GC to handle various data types beyond gradients, such as model parameters or activations. This would necessitate investigating how LLMs can effectively capture the diverse structures within these data modalities and adapting the serialization and compression techniques accordingly. Another promising avenue is integrating LM-GC with lossy compression methods in a more sophisticated way, potentially allowing for a hybrid approach that balances compression efficiency and precision. For example, LM-GC could be used to compress the most salient parts of the gradients losslessly, while employing quantization or sparsification for the less critical components. Finally, a thorough investigation into the impact of LLM architecture and training data on the effectiveness of LM-GC is needed. Exploring different pre-trained LLMs and experimenting with LLMs trained specifically on gradient data might unlock significant performance gains. These improvements would advance general gradient compression techniques and benefit diverse machine learning applications.
More visual insights#
More on figures
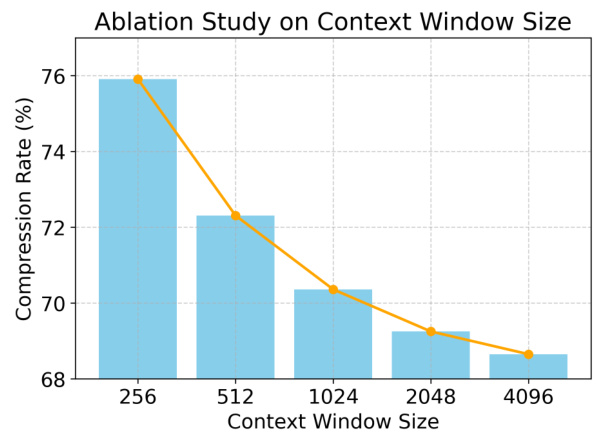
🔼 This figure shows an ablation study on the effect of different context window sizes on the compression rate achieved by the LM-GC method using the LLAMA 2-7B language model. The x-axis represents the context window size (in tokens), while the y-axis shows the resulting compression rate (percentage). As the context window increases, the model has more information to work with, leading to improved compression rates. The graph illustrates the trade-off between context size and computational cost.
read the caption
Figure 2: Compression rates of LLAMA 2-7B using context window sizes of 256, 512, 1024, 2048, and 4096. The compression rates improve as the context window increases.
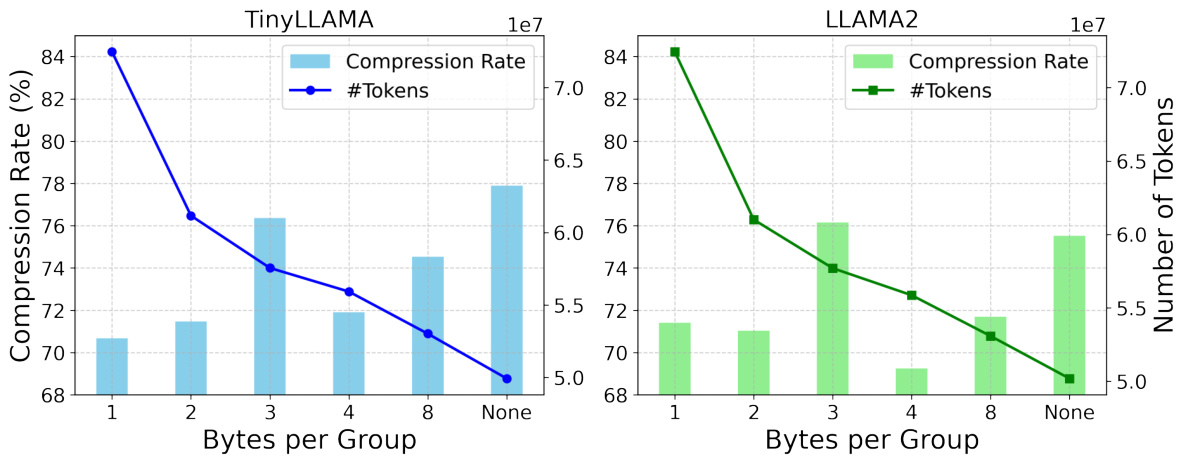
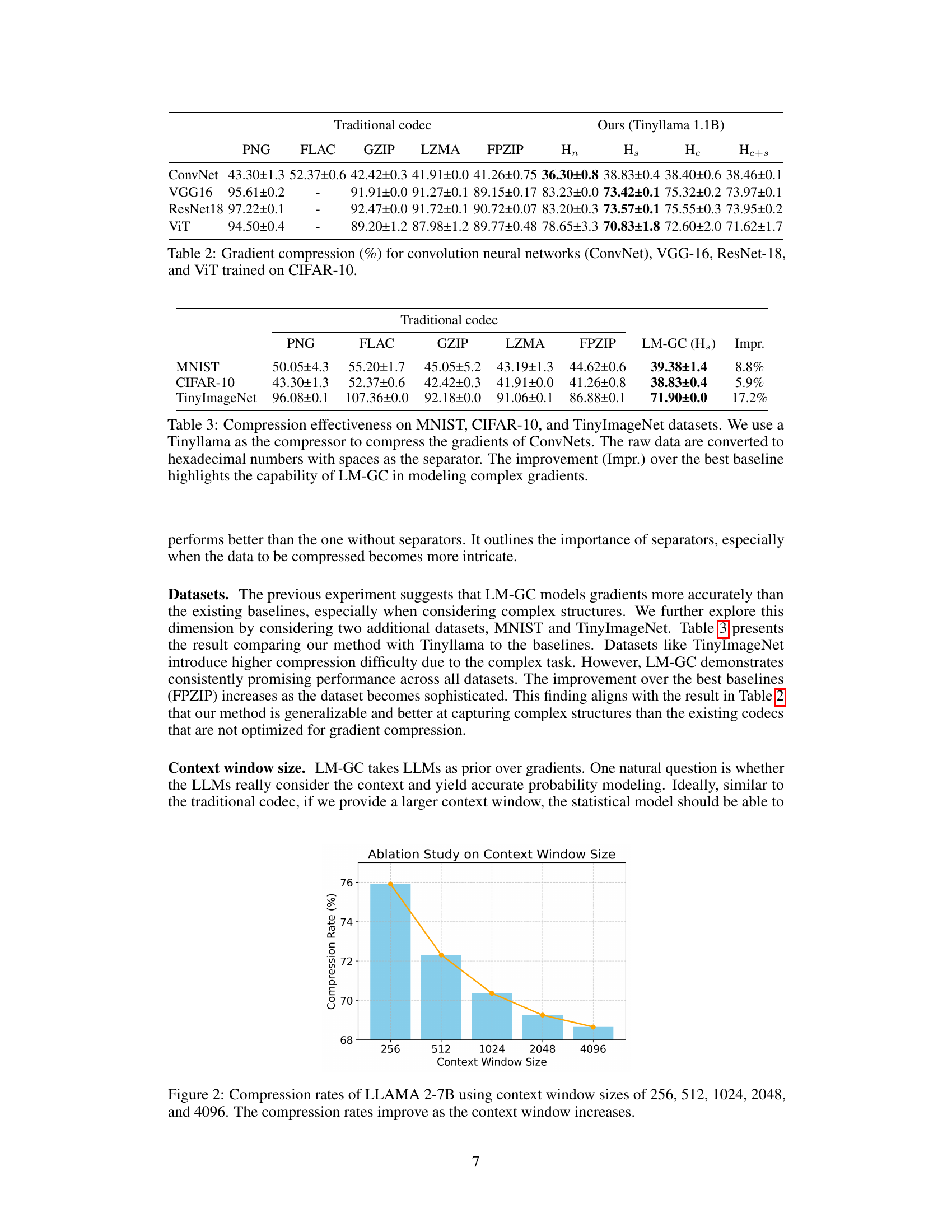
🔼 This figure shows the results of an ablation study on the number of bytes grouped together during the serialization process of LM-GC. It compares different serialization methods, varying the number of bytes grouped (1, 2, 3, 4, 8 bytes, and no grouping). The results demonstrate that grouping bytes according to the underlying structure of the floating-point numbers (4 bytes for each float) leads to better compression rates and fewer tokens used. While smaller group sizes increase computational overhead due to more tokens, following the data structure improves efficiency.
read the caption
Figure 3: Ablation study on numbers of grouped bytes. We report the compression rates and the number of tokens yielded by different serializations. The settings that closely obey the data format perform better. However, smaller numbers yield higher computation overhead.
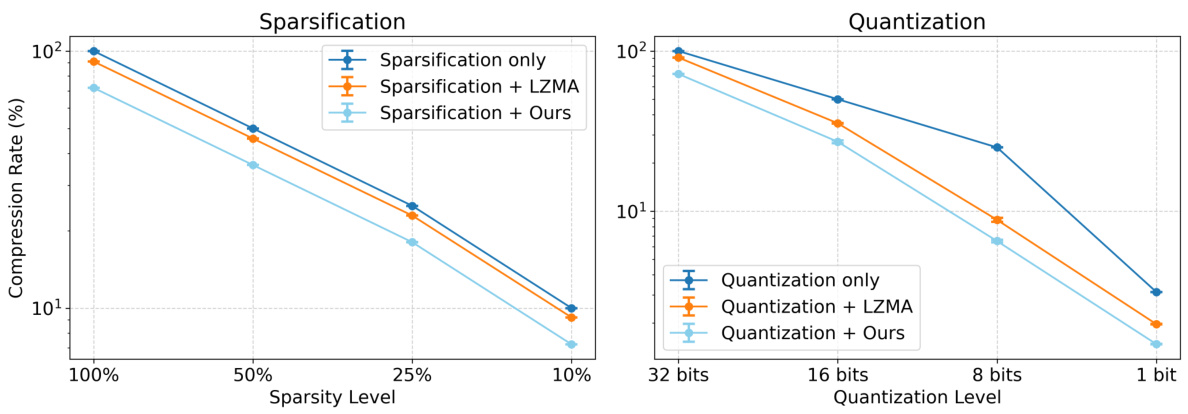
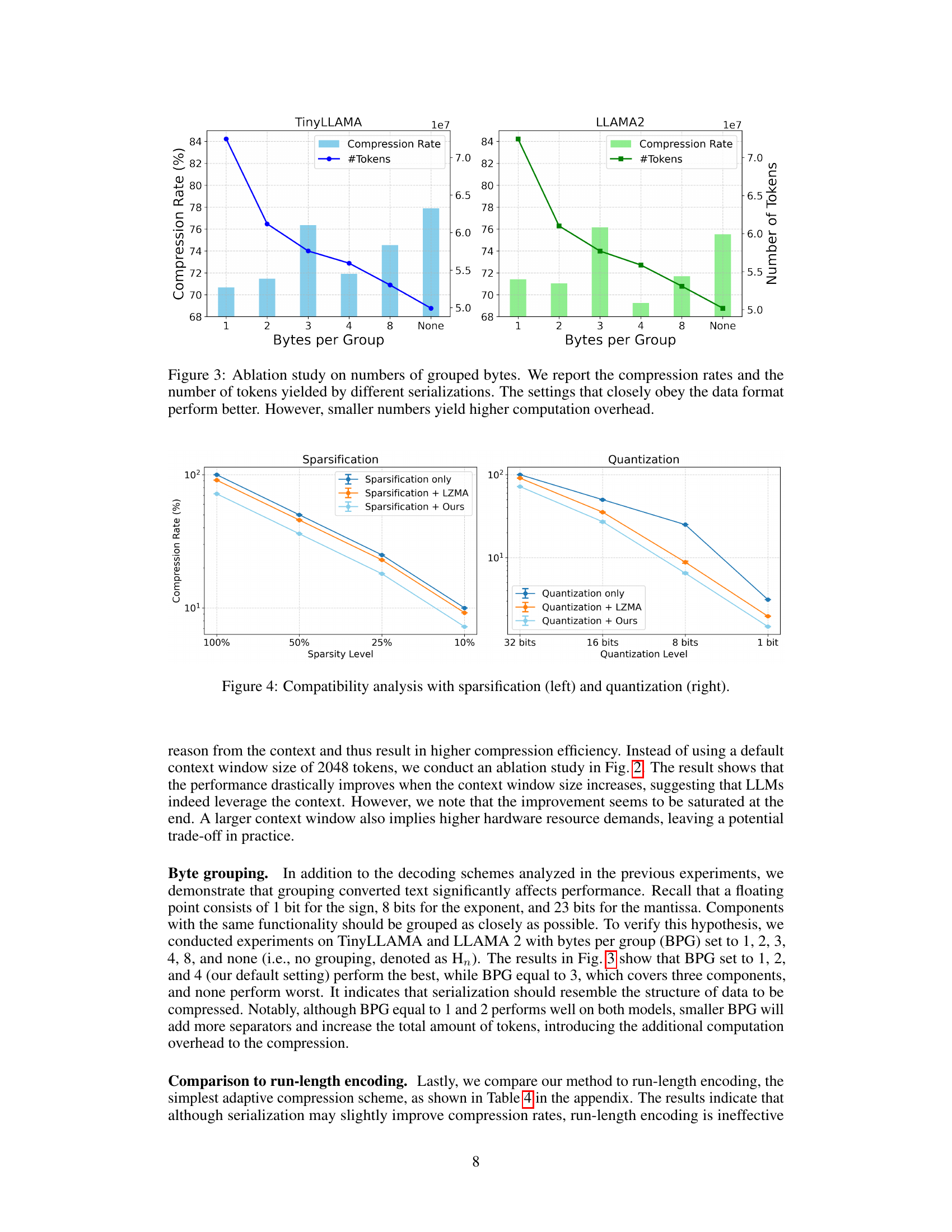
🔼 This figure demonstrates the compatibility of the proposed LM-GC method with existing lossy compression techniques: sparsification and quantization. The left panel shows how combining LM-GC with sparsification (reducing the number of gradient elements transmitted) leads to better compression ratios than using sparsification alone or with LZMA compression. The right panel illustrates similar results for quantization (reducing the precision of each gradient element). In both cases, LM-GC improves compression ratios regardless of the sparsification or quantization level.
read the caption
Figure 4: Compatibility analysis with sparsification (left) and quantization (right).
More on tables
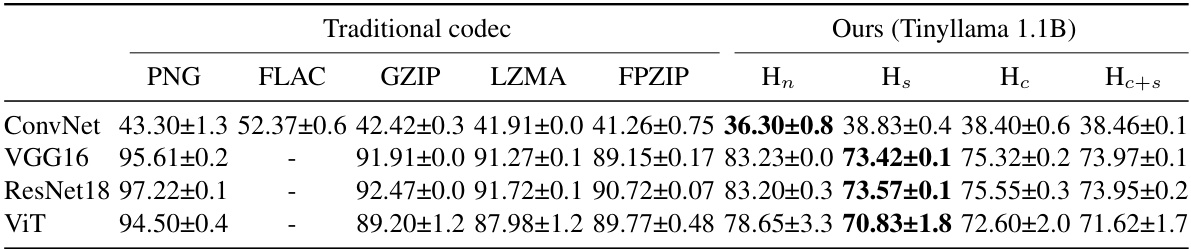
🔼 This table compares the gradient compression rates achieved by several traditional lossless compression methods (PNG, FLAC, GZIP, LZMA, FPZIP) against the proposed LM-GC method. LM-GC is tested with different LLMs and several serialization techniques (ISO-8859-1 encoding, hexadecimal representation with and without separators). The table highlights the superior compression rates achieved by LM-GC, especially when using appropriate serialization methods that improve LLM understanding of the gradient data structure.
read the caption
Table 1: Gradient compression rate using PNG, FLAC, GZIP, LZMA, FPZIP, and our method with various language models. Our method considers different serializations including iso-8859-1 (ISO), hexadecimal numbers without separators (Hn) and with spaces (Hs), commas (Hc), commas+spaces (Hc+s), and semicolons (Hsemi) to group every four bytes from the same floating point.

🔼 This table compares the compression rates achieved by LM-GC against several baseline codecs (PNG, FLAC, GZIP, LZMA, FPZIP) on three image datasets of varying complexity: MNIST, CIFAR-10, and TinyImageNet. The LM-GC method uses a Tinyllama language model and a specific serialization method (hexadecimal with spaces). The ‘Impr.’ column shows the percentage improvement of LM-GC over the best-performing baseline for each dataset.
read the caption
Table 3: Compression effectiveness on MNIST, CIFAR-10, and TinyImageNet datasets. We use a Tinyllama as the compressor to compress the gradients of ConvNets. The raw data are converted to hexadecimal numbers with spaces as the separator. The improvement (Impr.) over the best baseline highlights the capability of LM-GC in modeling complex gradients.

🔼 This table compares the compression rates achieved by Run Length Encoding (RLE) with different encoding schemes (binary, hexadecimal with and without separators) against the LM-GC method proposed in the paper. It demonstrates the inefficiency of RLE for compressing gradients, particularly compared to LM-GC, even with various adaptations to the RLE approach. The results highlight the superiority of LM-GC in effectively compressing gradient data.
read the caption
Table 4: Run length encoding results of gradients collected from ConvNets trained on TinyImageNet.
Full paper#