TL;DR#
Online multiclass prediction aims to make accurate probabilistic predictions over multiple classes. A key challenge lies in simultaneously minimizing regret across various loss functions, a problem addressed by U-calibration. However, determining the optimal U-calibration error remained an open problem. This research focuses on improving online multiclass prediction by developing a better understanding of U-calibration error. Previous works show that existing methods have limitations in achieving low U-calibration error, particularly for a large number of classes.
This research makes significant strides in resolving this challenge. By employing a modified Follow-the-Perturbed-Leader algorithm and constructing specific proper loss functions, the authors prove that the minimax optimal U-calibration error is indeed Θ(√KT). Furthermore, they demonstrate that logarithmic U-calibration error is achievable for specific classes of losses such as Lipschitz and decomposable losses, significantly improving upon previous results. These findings offer significant improvements and a better theoretical understanding to the existing algorithms for online multiclass prediction.
Key Takeaways#
Why does it matter?#
This paper significantly advances online multiclass prediction by establishing the optimal U-calibration error bound and providing improved bounds for specific loss function classes. It resolves an open question from Kleinberg et al. (2023) and offers valuable insights for researchers working on online learning and decision-making under uncertainty. Its findings on minimax optimal bounds and improved bounds for Lipschitz and decomposable losses open new avenues for algorithm design and theoretical analysis, impacting various applications of online sequential prediction.
Visual Insights#
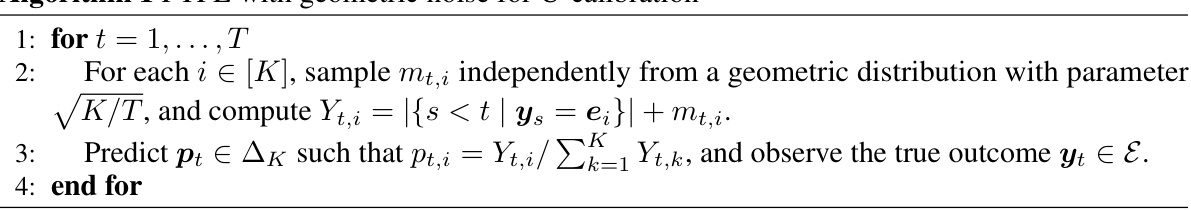
🔼 This algorithm is a modified version of the Follow-the-Perturbed-Leader (FTPL) algorithm. The key change is in how the noise is generated; instead of using a uniform distribution, it samples from a geometric distribution with parameter √K/T. This modification improves the algorithm’s performance in terms of pseudo U-calibration error, reducing it from O(K√T) to O(√KT). The algorithm iteratively predicts a distribution over K classes and then observes the true outcome to update its prediction for the next round.
read the caption
Algorithm 1 FTPL with geometric noise for U-calibration
Full paper#



















