TL;DR#
Many real-world problems involve discrete data (e.g., words, pixels), while continuous diffusion models have shown promise in generating high-quality data. However, directly applying these models to discrete data faces challenges due to the mismatch between the continuous nature of the model and the discrete nature of the data. Previous attempts to address this have fallen short in terms of performance and efficiency. This paper identifies the lack of discrete boundary guidance during model training as a major source of these limitations.
To overcome this, the researchers propose a novel two-step framework. First, they estimate the boundaries of the discrete data space as a prior distribution. Second, they rescale the forward diffusion trajectory to ensure the model’s learned probability contours align accurately with these boundaries. This boundary-conditional diffusion model is then applied to language modeling and image generation tasks, demonstrating impressive performance improvements. The results show significantly better performance compared to existing approaches, achieving state-of-the-art in three machine translation tasks, one summarization task, and categorical image generation on CIFAR-10.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working in discrete data modeling and diffusion processes. It directly addresses the critical issue of adapting powerful continuous diffusion models to the discrete data prevalent in many applications (like NLP and image generation). The proposed methodology offers significant performance improvements and establishes a new state-of-the-art in several tasks, making it highly relevant to current research trends. The study’s novel approach opens promising avenues for further research into boundary-conditional diffusion models and improved discrete data generation.
Visual Insights#
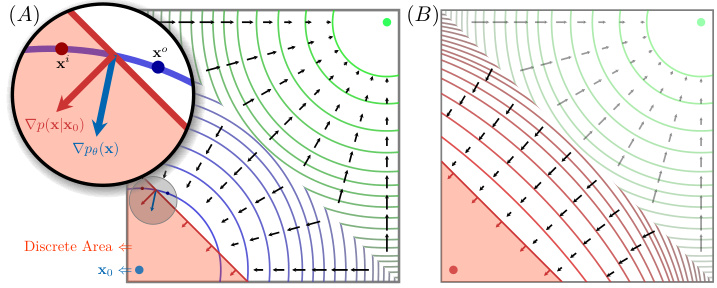
🔼 This figure illustrates the core problem addressed in the paper: the discrepancy between the probability density contours learned by continuous diffusion models and the boundaries of discrete data. (A) shows how learned contours (blue and green) deviate from the actual discrete area boundary (red), leading to imprecise data generation. (B) proposes a solution by incorporating discrete area boundaries as priors to guide the learning process and improve the precision of the probability distribution.
read the caption
Figure 1: (A) Blue and green curves are the learned probability density contours of the diffusion model for two data points. The red area is the discrete area of the blue data x0 and the boundary of this area is naturally a density contour. The discrete boundary is a complex hypersurface in the high-dimensional continuous space and we simplify it into a red line for convenience of description. As observed in the magnified part, the learned contours deviate from the boundary contour, resulting in inconsistent probability densities and gradient directions. (B) We consider the discrete boundary as priors for the diffusion process to estimate a more appropriate probability distribution, where the learned contours are expected to follow the shape of the discrete boundary.

🔼 This table presents the results of the proposed approach and several baselines on four different tasks: three machine translation tasks (IWSLT14 DE-EN, WMT14 EN-DE, WMT16 EN-RO) and one text summarization task (GIGAWORD). For each task, the table shows the BLEU scores (BLEU-1/2/3/4) for machine translation tasks and ROUGE scores (ROUGE-1/2/L) for the summarization task. The baselines include various autoregressive and diffusion-based language models. The table highlights the superior performance of the proposed method, particularly compared to other diffusion models, and its competitive performance against autoregressive transformers.
read the caption
Table 1: Result of BLEU scores on machine translation and ROUGE scores on text summarization.
In-depth insights#
Boundary Guidance#
The concept of ‘Boundary Guidance’ in the context of a research paper likely refers to techniques that constrain or influence a model’s learning process using boundary information. This is particularly relevant when dealing with discrete data or when aiming for more precise control over model outputs. Effective boundary guidance can mitigate issues arising from the mismatch between continuous model representations and the discrete nature of the data itself. For example, in discrete image generation, boundaries can define the valid range of pixel values, preventing the model from generating unrealistic or nonsensical outputs. In language modeling, boundaries might be defined by grammatical rules or semantic constraints. The implementation of boundary guidance can vary, from directly incorporating boundary information into the loss function to using more advanced techniques like conditional diffusion models or other constrained optimization strategies. The success of boundary guidance hinges on the quality and precision of the boundary information provided, and the method’s effectiveness would be critically dependent on the problem domain and model architecture. The key benefits include enhanced model control, improved accuracy in discrete data generation, and preventing unrealistic outputs.
ODE Forward Process#
Utilizing ordinary differential equations (ODEs) to model the forward diffusion process offers a deterministic approach, a key advantage over stochastic methods. This deterministic nature facilitates precise control and prediction of the noise injection process, crucial for the paper’s boundary conditional diffusion framework. By employing ODEs, the model effectively tracks the evolution of data points as noise is progressively added, ensuring a smooth and predictable path. This contrasts with stochastic methods where the noise injection is inherently random. The use of ODEs also enables precise calculation of the stopping time, when the forward trajectory intersects the discrete boundary, providing critical timing information for the subsequent rescaling steps. This precise stopping time is fundamental for the accuracy of the boundary-conditional rescaling, a central element of the proposed method. The ODE approach, therefore, provides both computational efficiency and enhanced accuracy, making it a powerful tool in discrete data generation within the context of diffusion processes.
Discrete Priors#
The concept of “Discrete Priors” in the context of diffusion models for discrete data generation is a crucial contribution. It addresses the core challenge of aligning continuous diffusion processes with discrete data, a mismatch that conventional methods struggle to overcome. By introducing discrete boundaries as prior distributions, the method guides the learning process towards more accurate probability contours that better reflect the true discrete nature of the data. This is a significant departure from existing approaches that often rely on simplistic, point-based representations of discrete data, which can lead to inaccuracies and blurred boundaries. The two-step forward process—first estimating boundaries, then rescaling trajectories—is elegant and effectively resolves the discrepancy between learned probability densities and the actual discrete areas. The methodology demonstrates a deep understanding of the underlying limitations of continuous diffusion models applied to discrete data and offers a powerful, principled approach to improve performance significantly. The success in both language modeling and image generation underscores the robustness and generalizability of this novel approach.
Rescaled Trajectories#
The concept of “Rescaled Trajectories” in the context of discrete modeling using diffusion processes is crucial. It addresses the fundamental mismatch between continuous diffusion models and discrete data. The core idea involves first estimating the boundaries of discrete data regions (e.g., words in language modeling) as prior distributions. Then, the forward diffusion trajectory, which adds noise to the data, is rescaled to ensure it respects these boundaries. This rescaling concentrates the probability density toward the boundary, ensuring the model learns precise discrete data representations, unlike previous methods which suffer from inaccuracies due to a lack of boundary guidance. The rescaling process is crucial to the success of this method as it corrects for an oversimplification in existing approaches that results in a mismatch between the model’s probability contours and true discrete regions. The reverse process, which recovers data from noise, is proportionally adjusted to maintain consistency. This two-step method, boundary estimation followed by trajectory rescaling, ultimately leads to improved results in both language modeling and image generation, overcoming a major limitation of directly applying continuous diffusion to discrete datasets.
Future Directions#
Future research could explore extending the framework to handle more complex data modalities beyond text and images, such as audio, video, and 3D point clouds. Investigating the theoretical properties of boundary conditional diffusion more rigorously could lead to improved efficiency and stability. Addressing the limitations of relying on boundary estimation is crucial, as inaccuracies could significantly affect performance. Developing more efficient algorithms for boundary estimation or alternative methods for incorporating discrete information into continuous diffusion processes would be highly valuable. Exploring the applications of the proposed approach in diverse domains like scientific discovery, drug design and healthcare diagnosis is warranted. Finally, comparing the proposed framework’s performance against other advanced discrete data generation models, especially those based on autoregressive approaches and other innovative generative methods, will be essential to understand its true potential and limitations.
More visual insights#
More on figures

🔼 This figure illustrates the core idea of the proposed method. Panel (A) shows how the probability density contours are rescaled to fit the discrete boundaries, and panel (B) illustrates how the forward trajectory is rescaled to make the sampling process conditioned on the boundary. The process involves estimating the boundary as a prior distribution and then rescaling the forward trajectory.
read the caption
Figure 2: (A) Rescaled Probability Contours. The bold curve xto is the density contour of one standard deviation. As the time t decreases from T to 0, the rescaled contours will gradually fit the discrete boundary and probability densities will also concentrate to this boundary. (B) Rescaled Forward Trajectory. Original forward trajectory x0 → xto → xt is rescaled to be a boundary conditional trajectory x1 → xt that starts from x1 = xto. The rescaled forward distribution pt(xt|x0) is transformed from the discrete boundary to Gaussian distributions.

🔼 This figure compares the image generation results of three different models on the CIFAR-10 dataset. (A) shows the results from a reproduced version of the Bit Diffusion model, which serves as a baseline. (B) presents the results from DDIM, another established diffusion model. Finally, (C) displays the results obtained using the novel boundary conditional diffusion process proposed in the paper. The figure visually demonstrates the improved image quality achieved by the proposed method, particularly in terms of detail and realism compared to the baseline models.
read the caption
Figure 3: Generated images of Bit Diffusion repro, DDIM, and Ours on CIFAR-10.

🔼 This figure compares the trajectory differences between three different diffusion process: Markovian Diffusion Process, Deterministic Diffusion Process, and Flow Matching. It visually shows how the forward and reverse processes unfold in each approach, highlighting the differences in the way noise is added and removed. This helps illustrate the core differences between the three methods used in the paper for modeling diffusion processes.
read the caption
Figure 4: We demonstrate the trajectory differences among Markovian Diffusion Process, Deterministic Diffusion and Flow Matching.

🔼 This figure shows the image generation results of three different methods on the CIFAR-10 dataset. (A) shows the results from a reproduced version of Bit Diffusion, (B) shows results from DDIM, and (C) shows the results from the proposed method in the paper. The figure visually compares the image quality and diversity generated by each method.
read the caption
Figure 3: Generated images of Bit Diffusion repro, DDIM, and Ours on CIFAR-10.

🔼 This figure shows the qualitative results of image generation using two different models on the CIFAR-10 dataset. The images generated by the reproduced Bit Diffusion model show artifacts and blurriness, indicating that the model struggled to capture fine details and textures. In contrast, images generated by the proposed ‘Ours’ model exhibit sharper details, more realistic textures, and less blurriness, highlighting the improved performance of the new method.
read the caption
Figure 5: Generated TRAINABLE EMBEDDING images of reproduced Bit Diffusion and Ours on CIFAR-10.

🔼 This figure compares the image generation results of the reproduced Bit Diffusion model and the proposed model on the CIFAR-10 dataset using trainable embedding. The images generated by the proposed model show a significant improvement in image quality and detail compared to the reproduced Bit Diffusion model, indicating that the proposed method effectively leverages trainable embeddings to generate higher-quality discrete images.
read the caption
Figure 7: Generated TRAINABLE EMBEDDING images of reproduced Bit Diffusion and Ours on CIFAR-10.
More on tables

🔼 This table presents the results of the proposed method and several baselines on four tasks: three machine translation tasks (IWSLT14 DE-EN, WMT14 EN-DE, WMT16 EN-RO) and one text summarization task (GIGAWORD). The results are shown in terms of BLEU scores (BLEU-1/2/3/4) for the translation tasks and ROUGE scores (ROUGE-1/2/L) for the summarization task. It compares the performance of the proposed approach against autoregressive transformers and several existing continuous and discrete diffusion language models.
read the caption
Table 1: Result of BLEU scores on machine translation and ROUGE scores on text summarization.
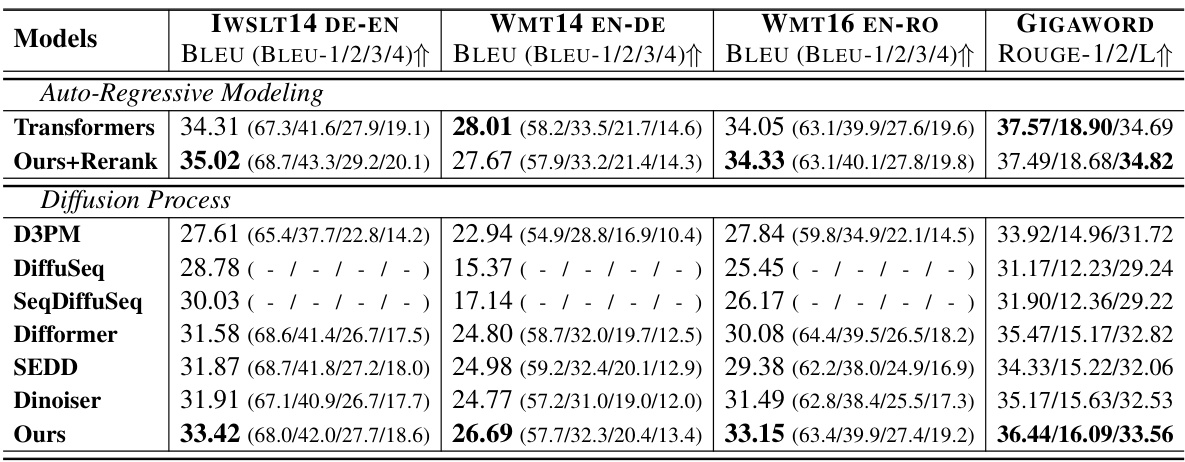
🔼 This table presents the performance comparison of different models on four tasks: three machine translation tasks (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO) and one text summarization task (GIGAWORD). The models are categorized into Auto-Regressive Modeling and Diffusion Process. For each task, BLEU scores (1-4) are reported for machine translation tasks, and ROUGE scores (1,2,L) for the summarization task. The table allows readers to compare the performance of the proposed ‘Ours’ model against state-of-the-art autoregressive and diffusion models.
read the caption
Table 1: Result of BLEU scores on machine translation and ROUGE scores on text summarization.

🔼 This table presents the results of an ablation study comparing different training objectives used in the model. It shows the error in predicting x0 (the original data), the error in predicting the vector field, the accuracy of predicting whether x0 is within the discrete area (Cxo), and the final BLEU score achieved on a machine translation task. The comparison helps to determine which objective function yields the best performance.
read the caption
Table 3: Analysis on the training objectives.
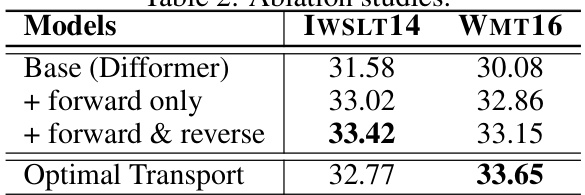
🔼 This table presents the ablation study results, comparing the performance of the proposed model with different configurations against the baseline model (Difformer). The configurations include using only the forward process, using both forward and reverse processes, and using optimal transport for trajectory rescaling. The results are evaluated using BLEU scores on the IWSLT14 DE-EN and WMT16 EN-RO datasets.
read the caption
Table 2: Ablation studies.

🔼 This table presents the Fréchet Inception Distance (FID) scores achieved by different models on the CIFAR-10 image dataset. It compares the performance of various methods, including continuous diffusion models (DDPM, DDIM), discrete ordinal pixel models (D3PM, TLDR), and the proposed boundary conditional diffusion models using different image representations (binary coding, fixed embedding, and trainable embedding). Lower FID scores indicate better image generation quality.
read the caption
Table 4: FID scores on CIFAR-10.
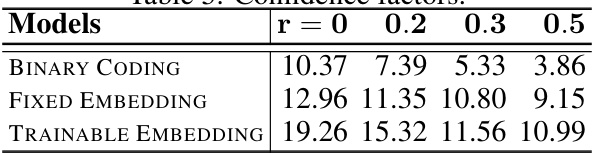
🔼 This table shows the FID scores on CIFAR-10 for different image generation settings using three different discrete image representations (Binary Coding, Fixed Embedding, and Trainable Embedding). The results are shown for various values of the confidence factor ‘r’, ranging from 0 to 0.5. A confidence factor of 0 represents the original diffusion process (without discrete priors), while higher values indicate increased reliance on the discrete boundaries. The FID score is a measure of image quality, with lower scores indicating higher quality. The table demonstrates the effect of the confidence factor on the generated image quality for each image representation.
read the caption
Table 5: Confidence factors.
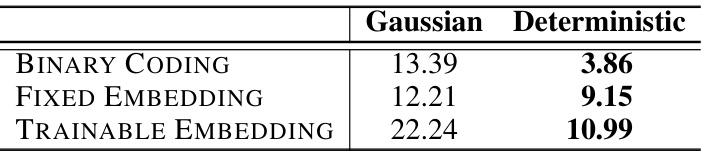
🔼 This table presents the Fréchet Inception Distance (FID) scores achieved by different models on the CIFAR-10 dataset. The FID score is a metric used to evaluate the quality of generated images. Lower FID scores indicate better image quality. The table compares the performance of the proposed approach using various discrete image representations (Binary Coding, Fixed Embedding, Trainable Embedding) and sampling methods (Gaussian, Deterministic). It also includes comparisons to baseline methods like DDPM and DDIM.
read the caption
Table 4: FID scores on CIFAR-10.

🔼 This table presents the results of the proposed approach and several baselines on four different tasks: three machine translation tasks (IWSLT14 DE-EN, WMT14 EN-DE, and WMT16 EN-RO) and one text summarization task (GIGAWORD). The BLEU scores (BLEU-1/2/3/4) measure the performance of machine translation, while the ROUGE scores (ROUGE-1/2/L) evaluate the performance of text summarization. The table compares the proposed approach against several autoregressive and diffusion-based models, highlighting its superior performance in several cases. The ‘Ours + Rerank’ row indicates that reranking improved results further.
read the caption
Table 1: Result of BLEU scores on machine translation and ROUGE scores on text summarization.
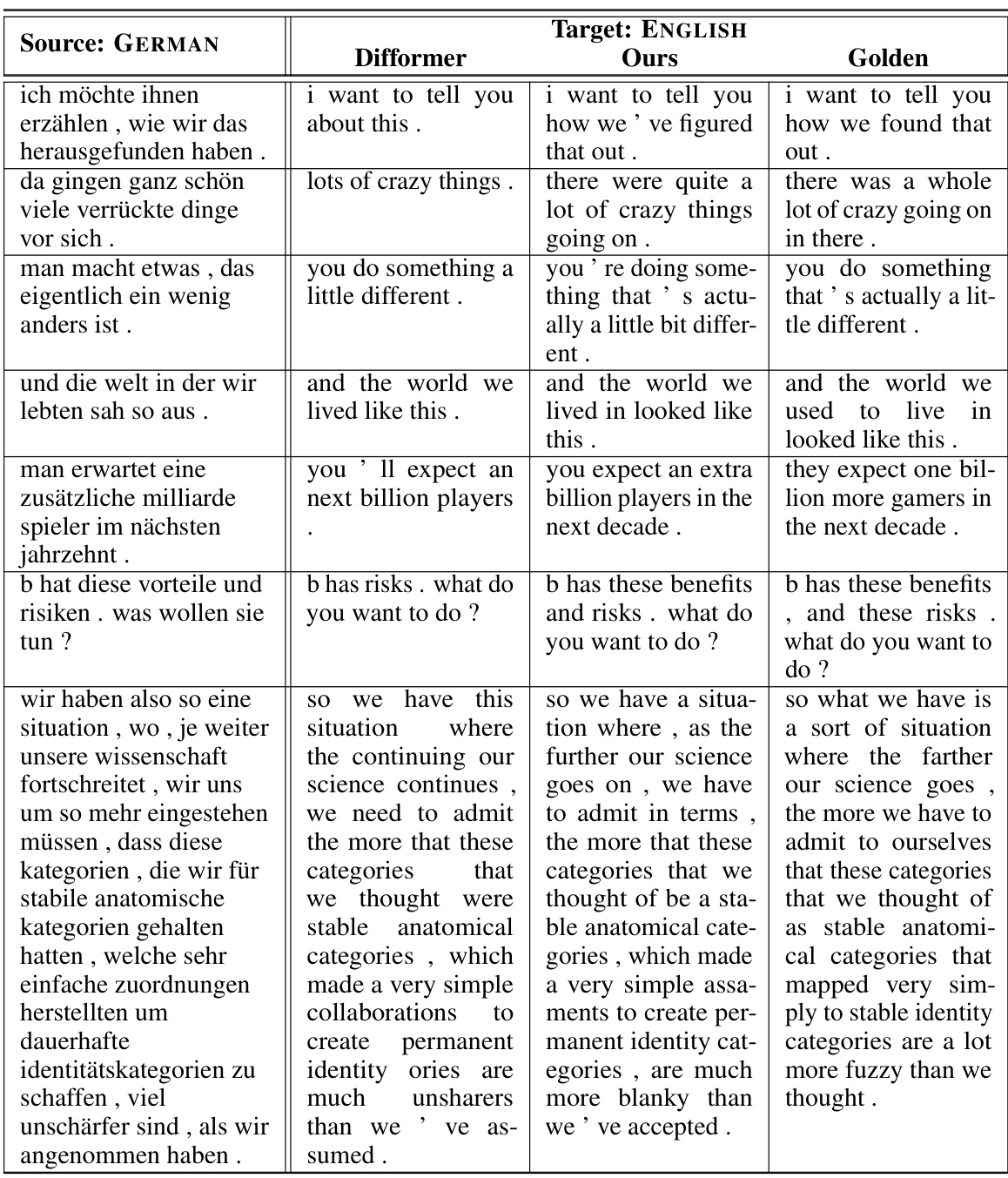
🔼 This table presents the performance comparison of different models on machine translation and text summarization tasks. It shows BLEU scores (BLEU-1/2/3/4) for three machine translation datasets (IWSLT14 DE-EN, WMT14 EN-DE, WMT16 EN-RO) and ROUGE scores (ROUGE-1/2/L) for a text summarization dataset (GIGAWORD). The models compared include autoregressive transformers, several continuous diffusion models (D3PM, DiffuSeq, SeqDiffuSeq, Difformer, SEDD, Dinoiser), and the proposed ‘Ours’ model. The table highlights the superior performance of the proposed model, particularly surpassing previous state-of-the-art continuous diffusion language models and achieving competitive results compared to autoregressive transformers.
read the caption
Table 1: Result of BLEU scores on machine translation and ROUGE scores on text summarization.

🔼 This table presents the performance comparison of different models on machine translation and text summarization tasks. The models compared include autoregressive transformers and various diffusion models. The evaluation metrics are BLEU scores (BLEU-1, BLEU-2, BLEU-3, BLEU-4) for machine translation and ROUGE scores (ROUGE-1, ROUGE-2, ROUGE-L) for summarization. The results show how well each model performs compared to the state-of-the-art in these tasks.
read the caption
Table 1: Result of BLEU scores on machine translation and ROUGE scores on text summarization.
Full paper#



















