TL;DR#
Out-of-distribution (OOD) generalization, crucial for real-world AI, poses significant challenges in graph data. Existing invariant learning methods, like Invariant Risk Minimization (IRM) and Variance-Risk Extrapolation (VREx), often fail to identify true predictive patterns in node-level graph tasks, instead relying on spurious features. This limitation stems from their lack of class-conditional invariance constraints which leads to inaccurate structural understanding of predictive ego-graphs.
To overcome these issues, the researchers introduce Cross-environment Intra-class Alignment (CIA) and its label-free variant CIA-LRA. CIA explicitly aligns cross-environment representations within the same class, effectively removing spurious features. CIA-LRA adapts this approach to scenarios without environment labels by cleverly leveraging the distribution of neighboring labels. Theoretical analysis and experimental validation on multiple benchmarks confirm CIA and CIA-LRA’s effectiveness and advancement in node-level OOD generalization.
Key Takeaways#
Why does it matter?#
This paper is crucial because node-level out-of-distribution (OOD) generalization on graphs is a major challenge in machine learning. The work directly addresses this challenge by theoretically analyzing existing methods’ shortcomings and proposing novel, effective solutions. This advances the field and opens new avenues for robust graph-based AI systems. The provided code allows for reproducibility and further exploration.
Visual Insights#
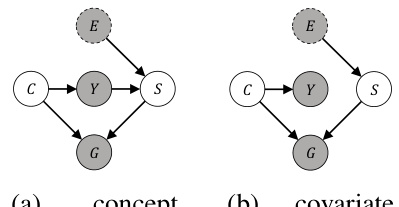
🔼 This figure shows two causal graphs representing the structural causal models (SCMs) used in the paper to characterize two types of distribution shifts: (a) concept shift and (b) covariate shift. In both cases, C represents the unobservable causal latent variable, S represents the unobservable spurious latent variable, Y represents the node label, G represents the observed graph, and E represents the environment variable. The dashed arrows indicate that the environment variable is not directly observed but affects the data generation process. The concept shift model shows that the causal latent variable directly influences the node labels, while the spurious latent variable influences the graph structure. The covariate shift model shows that the spurious variable influences the node features but not the node labels. These models help to explain how different types of distributional shifts can affect node-level out-of-distribution (OOD) generalization on graphs.
read the caption
Figure 1: Causal graphs of the SCMs considered in our work.
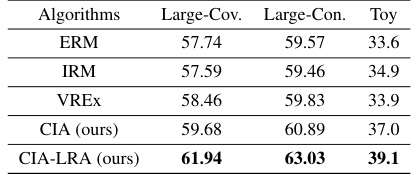
🔼 This table presents the Out-of-Distribution (OOD) accuracy results for several algorithms on various graph datasets. The algorithms compared include standard Empirical Risk Minimization (ERM), Invariant Risk Minimization (IRM), Variance-Risk Extrapolation (VREx), and the proposed Cross-environment Intra-class Alignment (CIA) and CIA-LRA methods. The datasets are categorized into real-world datasets (Arxiv, Cora, CBAS, WebKB) and a synthetic toy dataset. Results are broken down by covariate shift and concept shift, highlighting the performance of each algorithm under different distributional shifts.
read the caption
Table 1: Real-Cov./Con. are average OOD accuracy on the covariate/concept shift of Arxiv, Cora, CBAS, and WebKB. Toy denotes results on our toy synthetic graph OOD dataset.
In-depth insights#
Graph OOD Failure#
The heading ‘Graph OOD Failure’ encapsulates a critical challenge in applying invariant learning methods to graph-structured data. Traditional invariant learning techniques, designed for image or tabular data, often fail to generalize effectively to out-of-distribution (OOD) scenarios on graphs. This failure stems from the inherent complexities of graph data, including the interdependence of nodes within the graph structure and the presence of spurious correlations between features and labels. Unlike independent data points in image classification, a node’s label in a graph depends heavily on its local neighborhood, making it challenging to disentangle invariant and spurious signals. The paper likely delves into the reasons why simple adaptation of invariant learning methods doesn’t work, proposing explanations rooted in the unique characteristics of graph data and the limitations of existing methods. This necessitates novel approaches that address the interplay between graph structure and feature invariance for robust OOD generalization.
CIA Invariant Learning#
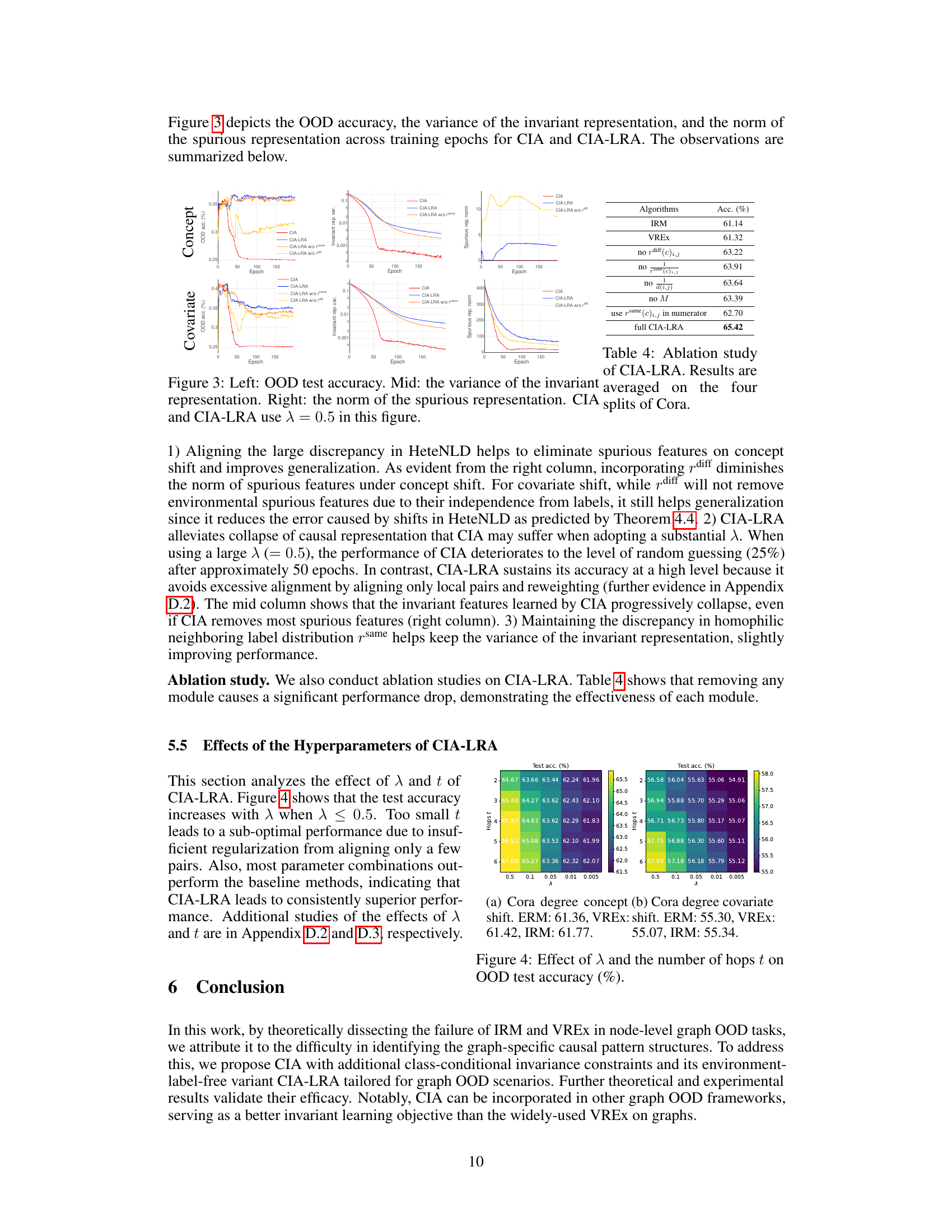
The concept of “CIA Invariant Learning” presented in the research paper proposes a novel approach to enhance node-level Out-of-Distribution (OOD) generalization in graph data. CIA, or Cross-environment Intra-class Alignment, directly addresses the limitations of existing invariant learning methods like IRM and VREx by explicitly aligning cross-environment representations conditioned on the same class. This crucial step bypasses the need for explicit knowledge of causal structure, a significant advantage over previous methods that often struggled to identify and leverage true invariant features. The core innovation is in how it eliminates spurious features by focusing on intra-class alignment across environments. This is particularly beneficial in scenarios where environment labels are scarce or unavailable, making it a practical and robust approach for real-world graph OOD problems. The method’s effectiveness is further enhanced by the introduction of CIA-LRA, a label-based variant of CIA that leverages the local distribution of neighboring labels to selectively align node representations, further improving accuracy and robustness.
CIA-LRA Adaptation#
The proposed CIA-LRA adaptation cleverly addresses the challenge of environment label unavailability in node-level out-of-distribution (OOD) generalization tasks. By leveraging the localized distribution of neighboring labels, CIA-LRA effectively bypasses the need for explicit environment labels while still achieving the goal of aligning cross-environment representations within the same class. This localized reweighting strategy is crucial, as it prevents the collapse of invariant features that could occur with indiscriminate alignment. Theoretical grounding is provided through a PAC-Bayesian analysis, deriving an OOD generalization error bound which validates the effectiveness of the approach. The integration of an invariant subgraph extractor further enhances performance by focusing the alignment on relevant portions of the graph. The overall design of CIA-LRA showcases a practical and theoretically sound solution to a significant problem within the field of graph-based machine learning.
Generalization Bounds#
Generalization bounds in machine learning offer a theoretical framework to quantify the difference between a model’s performance on training data and its expected performance on unseen data. They are crucial for understanding how well a model will generalize to new, unseen examples, a key concern in avoiding overfitting. Tight generalization bounds suggest strong generalization capabilities, meaning the model’s training performance is a reliable indicator of its future performance. Conversely, loose bounds imply greater uncertainty about how well the model will generalize, highlighting a need for further analysis or model refinement. The derivation of generalization bounds often involves complex mathematical techniques and relies on assumptions about the data distribution and model capacity. Different types of bounds exist (e.g., PAC-Bayesian, Rademacher complexity), each with its strengths and limitations. Analyzing generalization bounds provides valuable insights into model selection, algorithm design, and the overall robustness of machine learning systems. Understanding the assumptions underpinning these bounds is critical because their validity significantly impacts the reliability of the derived results.
Graph OOD Benchmarks#
Developing robust and reliable graph out-of-distribution (OOD) detection methods hinges critically on the availability of comprehensive benchmarks. A well-designed benchmark must encompass diverse graph structures, feature distributions, and types of OOD scenarios, such as concept shift and covariate shift. Existing benchmarks often lack sufficient diversity, limiting the generalizability of evaluated methods. Ideally, a benchmark should also include metadata such as causal relationships between features and labels, providing richer insights into the nature of OOD failures. This allows researchers to not only evaluate performance but also to diagnose the underlying reasons for OOD susceptibility, fostering the development of more effective and explainable OOD generalization techniques. A comprehensive benchmark will facilitate a more rigorous and meaningful comparison of different methods, pushing the field forward in addressing the challenges of OOD in graph data. Furthermore, a standardized evaluation protocol, including metrics and datasets, is essential to ensure reproducibility and facilitate collaboration.
More visual insights#
More on figures
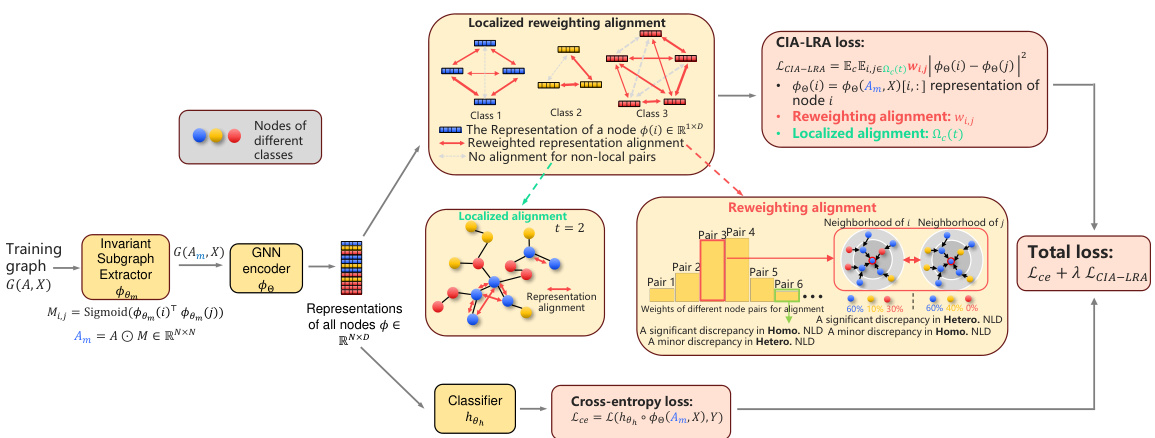
🔼 The figure illustrates the framework of the proposed CIA-LRA method, highlighting the invariant subgraph extractor, GNN encoder, localized alignment, reweighting alignment, and the total loss calculation. It emphasizes the method’s ability to identify invariant features and eliminate spurious ones, even without environment labels, by focusing on local node pairs and weighting them based on their neighborhood label distribution discrepancies.
read the caption
Figure 2. The overall framework of our proposed CIA-LRA. The invariant subgraph extractor Φθ identifies the invariant subgraph for each node. Then the GNN encoder φθ aggregates information from the estimated invariant subgraphs to output node representations. CIA-LRA mainly contains two strategies: localized alignment and reweighting alignment. Localized alignment: we restrict the alignment to a local range to avoid overalignment that may cause the collapse of invariant features (shown in Appendix D.1). Reweighting alignment: to better eliminate spurious features and preserve invariant features without using environment labels, we assign large weights to node pairs with significant discrepancies in heterophilic Neighborhood Label Distribution (NLD) and minor discrepancies in homophilic NLD. See Section 3.2 for a detailed analysis of CIA-LRA.
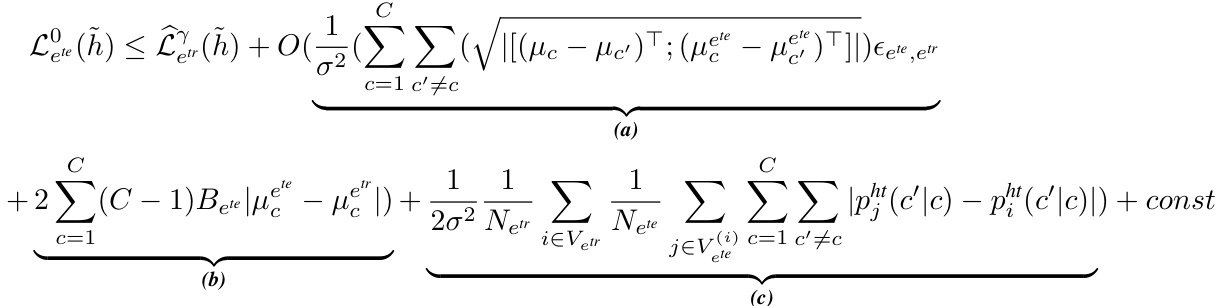
🔼 This figure illustrates the framework of the proposed CIA-LRA method, which is designed for node-level out-of-distribution generalization on graphs without environment labels. It details the steps of invariant subgraph extraction, GNN encoding, localized alignment (restricting alignment to local neighborhoods to avoid feature collapse), and reweighting alignment (prioritizing alignment of node pairs exhibiting significant discrepancies in heterophilic NLD and minor discrepancies in homophilic NLD to remove spurious features while preserving invariant ones).
read the caption
Figure 2: The overall framework of our proposed CIA-LRA. The invariant subgraph extractor Φθ identifies the invariant subgraph for each node. Then the GNN encoder de aggregates information from the estimated invariant subgraphs to output node representations. CIA-LRA mainly contains two strategies: localized alignment and reweighting alignment. Localized alignment: we restrict the alignment to a local range to avoid overalignment that may cause the collapse of invariant features (shown in Appendix D.1). Reweighting alignment: to better eliminate spurious features and preserve invariant features without using environment labels, we assign large weights to node pairs with significant discrepancies in heterophilic Neighborhood Label Distribution (NLD) and minor discrepancies in homophilic NLD. See Section 3.2 for a detailed analysis of CIA-LRA.
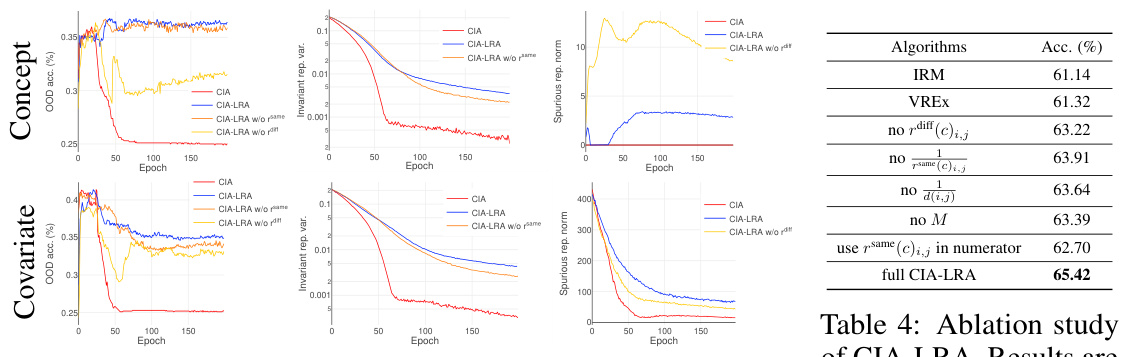
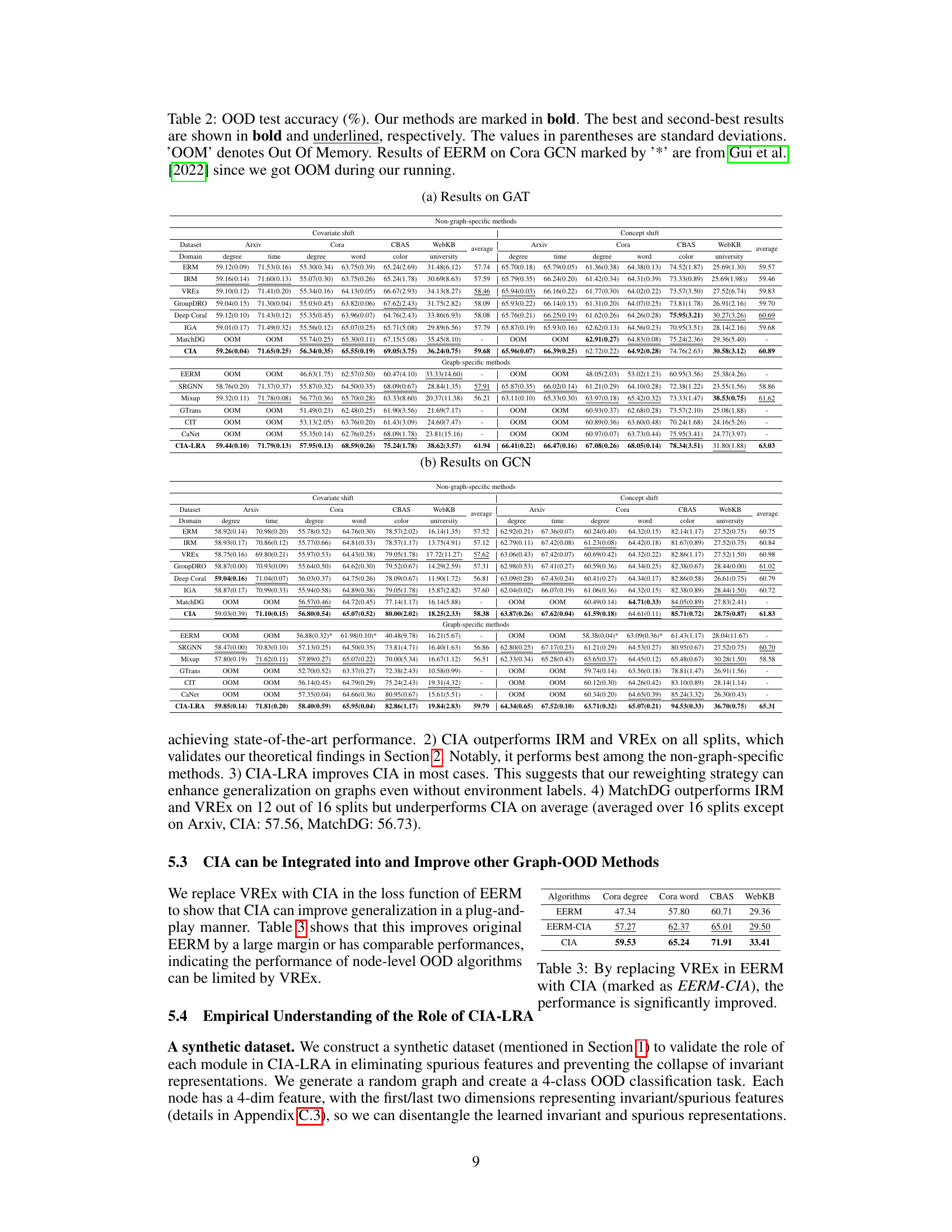
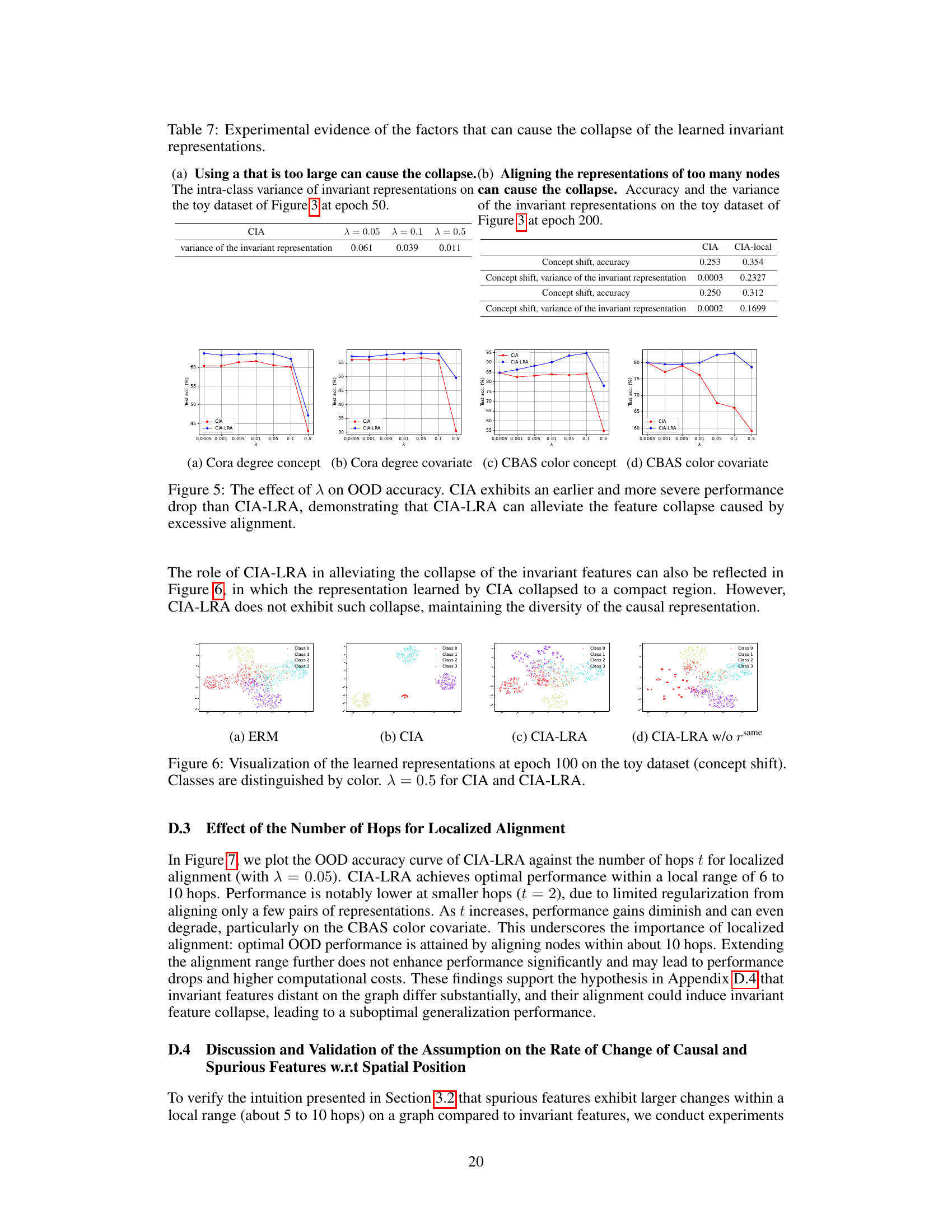
🔼 This figure shows the results of an ablation study comparing CIA and CIA-LRA on a synthetic dataset. The left column displays the out-of-distribution (OOD) accuracy over training epochs for both methods. The middle column shows the variance of the invariant representation, and the right column shows the norm of the spurious representation. The plots reveal that CIA-LRA is more effective at eliminating spurious features and preserving invariant features, leading to better OOD generalization performance compared to CIA, especially with a larger regularization parameter λ = 0.5.
read the caption
Figure 3: Left: OOD test accuracy. Mid: the variance of the invariant representation. Right: the norm of the spurious representation. CIA and CIA-LRA use λ = 0.5 in this figure.
🔼 The figure illustrates the framework of CIA-LRA, highlighting its key components: invariant subgraph extraction, GNN encoding, localized alignment, and reweighting alignment. Localized alignment focuses on aligning nearby nodes to prevent feature collapse, while reweighting alignment prioritizes aligning nodes with significant differences in heterophilic NLD and minor differences in homophilic NLD to eliminate spurious features. The method leverages localized label distribution to effectively distinguish and preserve invariant features.
read the caption
Figure 2: The overall framework of our proposed CIA-LRA. The invariant subgraph extractor Φθ identifies the invariant subgraph for each node. Then the GNN encoder de aggregates information from the estimated invariant subgraphs to output node representations. CIA-LRA mainly contains two strategies: localized alignment and reweighting alignment. Localized alignment: we restrict the alignment to a local range to avoid overalignment that may cause the collapse of invariant features (shown in Appendix D.1). Reweighting alignment: to better eliminate spurious features and preserve invariant features without using environment labels, we assign large weights to node pairs with significant discrepancies in heterophilic Neighborhood Label Distribution (NLD) and minor discrepancies in homophilic NLD. See Section 3.2 for a detailed analysis of CIA-LRA.
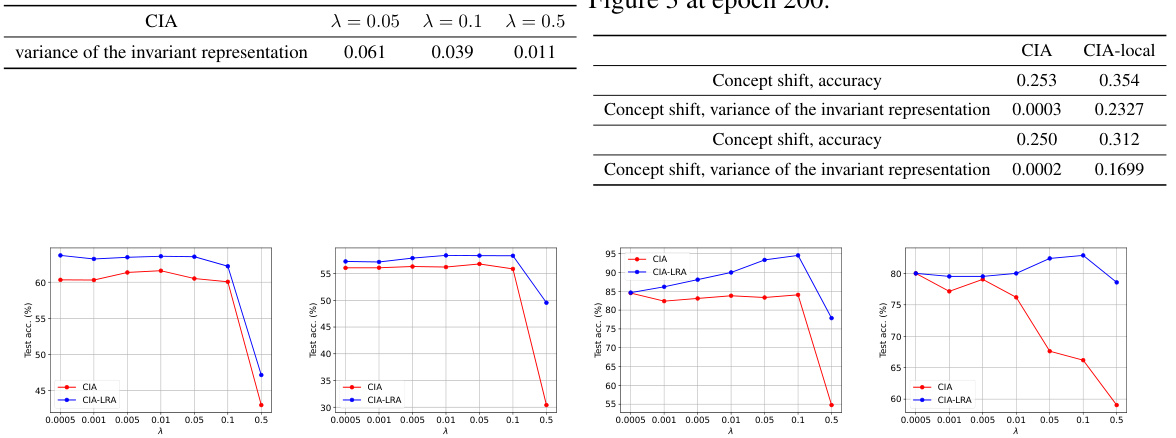
🔼 This figure shows the results of an ablation study comparing the performance of CIA and CIA-LRA on a synthetic dataset. The left panel displays OOD accuracy, demonstrating that CIA-LRA consistently maintains higher accuracy than CIA across training epochs. The middle panel shows the variance of the invariant representation, illustrating that CIA-LRA preserves higher variance, suggesting that it better maintains the invariant features. The right panel shows the norm (magnitude) of the spurious representation. CIA-LRA effectively reduces the norm of spurious features, confirming that spurious features are eliminated by the proposed method. Overall, the figure highlights that CIA-LRA’s ability to avoid collapsing the invariant features during training, which improves generalization performance.
read the caption
Figure 3: Left: OOD test accuracy. Mid: the variance of the invariant representation. Right: the norm of the spurious representation. CIA and CIA-LRA use λ = 0.5 in this figure.

🔼 This figure visualizes the impact of CIA and CIA-LRA on a synthetic dataset with concept and covariate shifts. The left panel displays OOD accuracy, demonstrating the superior performance of CIA-LRA. The middle panel shows the variance of invariant representations, highlighting how CIA-LRA maintains higher variance, preventing representation collapse. The right panel shows the norm of spurious representations, illustrating that both CIA and CIA-LRA effectively suppress them, but CIA-LRA is more effective. Overall, the figure shows that CIA-LRA offers better OOD generalization by effectively balancing the preservation of invariant features and the removal of spurious features.
read the caption
Figure 3: Left: OOD test accuracy. Mid: the variance of the invariant representation. Right: the norm of the spurious representation. CIA and CIA-LRA use λ = 0.5 in this figure.

🔼 This figure visualizes the effects of CIA and CIA-LRA on OOD generalization performance using a synthetic dataset. The left panel shows the OOD accuracy over training epochs for both methods. The middle panel displays the variance of the invariant representation, indicating the stability of the learned features. The right panel shows the norm of the spurious representation, reflecting the influence of irrelevant information. The results demonstrate that CIA-LRA is superior in maintaining the stability of invariant features while effectively reducing spurious ones, leading to better OOD generalization.
read the caption
Figure 3: Left: OOD test accuracy. Mid: the variance of the invariant representation. Right: the norm of the spurious representation. CIA and CIA-LRA use λ = 0.5 in this figure.
🔼 This figure illustrates the overall framework of the proposed CIA-LRA method for node-level out-of-distribution generalization on graphs. CIA-LRA leverages invariant subgraph extraction, localized alignment (to avoid feature collapse), and reweighted alignment (based on heterophilic and homophilic neighborhood label distributions) to learn invariant representations without relying on environment labels.
read the caption
Figure 2: The overall framework of our proposed CIA-LRA. The invariant subgraph extractor Φθ identifies the invariant subgraph for each node. Then the GNN encoder de aggregates information from the estimated invariant subgraphs to output node representations. CIA-LRA mainly contains two strategies: localized alignment and reweighting alignment. Localized alignment: we restrict the alignment to a local range to avoid overalignment that may cause the collapse of invariant features (shown in Appendix D.1). Reweighting alignment: to better eliminate spurious features and preserve invariant features without using environment labels, we assign large weights to node pairs with significant discrepancies in heterophilic Neighborhood Label Distribution (NLD) and minor discrepancies in homophilic NLD. See Section 3.2 for a detailed analysis of CIA-LRA.
🔼 This figure shows the overall framework of the proposed CIA-LRA method, which consists of an invariant subgraph extractor, a GNN encoder, localized alignment, and reweighting alignment. The invariant subgraph extractor identifies invariant subgraphs. The GNN encoder aggregates information from these subgraphs. Localized alignment aligns representations of nearby nodes to prevent over-alignment. Reweighting alignment assigns weights based on differences in heterophilic and homophilic neighborhood label distributions to eliminate spurious features while preserving invariant ones.
read the caption
Figure 2: The overall framework of our proposed CIA-LRA. The invariant subgraph extractor Φθ identifies the invariant subgraph for each node. Then the GNN encoder de aggregates information from the estimated invariant subgraphs to output node representations. CIA-LRA mainly contains two strategies: localized alignment and reweighting alignment. Localized alignment: we restrict the alignment to a local range to avoid overalignment that may cause the collapse of invariant features (shown in Appendix D.1). Reweighting alignment: to better eliminate spurious features and preserve invariant features without using environment labels, we assign large weights to node pairs with significant discrepancies in heterophilic Neighborhood Label Distribution (NLD) and minor discrepancies in homophilic NLD. See Section 3.2 for a detailed analysis of CIA-LRA.
🔼 This figure illustrates the framework of the proposed CIA-LRA method. It shows how invariant subgraphs are extracted for each node using a GNN encoder, and then how node representations are generated. It details the two main strategies of the method: localized alignment (restricting alignment to nearby nodes) and reweighting alignment (assigning higher weights to node pairs with significant differences in heterophilic NLD and minor differences in homophilic NLD to better eliminate spurious features).
read the caption
Figure 2: The overall framework of our proposed CIA-LRA. The invariant subgraph extractor Φθ identifies the invariant subgraph for each node. Then the GNN encoder de aggregates information from the estimated invariant subgraphs to output node representations. CIA-LRA mainly contains two strategies: localized alignment and reweighting alignment. Localized alignment: we restrict the alignment to a local range to avoid overalignment that may cause the collapse of invariant features (shown in Appendix D.1). Reweighting alignment: to better eliminate spurious features and preserve invariant features without using environment labels, we assign large weights to node pairs with significant discrepancies in heterophilic Neighborhood Label Distribution (NLD) and minor discrepancies in homophilic NLD. See Section 3.2 for a detailed analysis of CIA-LRA.
🔼 This figure illustrates the overall framework of the proposed CIA-LRA method. It shows how the method identifies invariant subgraphs, uses a GNN encoder to produce node representations, and employs localized and reweighting alignment strategies to eliminate spurious features and preserve invariant features, all while not requiring environment labels. The localized alignment restricts alignment to a local graph area, while the reweighting alignment prioritizes aligning node pairs that show significant differences in heterophilic neighborhood label distribution (HeteNLD) and minor differences in homophilic NLD.
read the caption
Figure 2: The overall framework of our proposed CIA-LRA. The invariant subgraph extractor ϕθm identifies the invariant subgraph for each node. Then the GNN encoder ϕΘ aggregates information from the estimated invariant subgraphs to output node representations. CIA-LRA mainly contains two strategies: localized alignment and reweighting alignment. Localized alignment: we restrict the alignment to a local range to avoid overalignment that may cause the collapse of invariant features (shown in Appendix D.1). Reweighting alignment: to better eliminate spurious features and preserve invariant features without using environment labels, we assign large weights to node pairs with significant discrepancies in heterophilic Neighborhood Label Distribution (NLD) and minor discrepancies in homophilic NLD. See Section 3.2 for a detailed analysis of CIA-LRA.
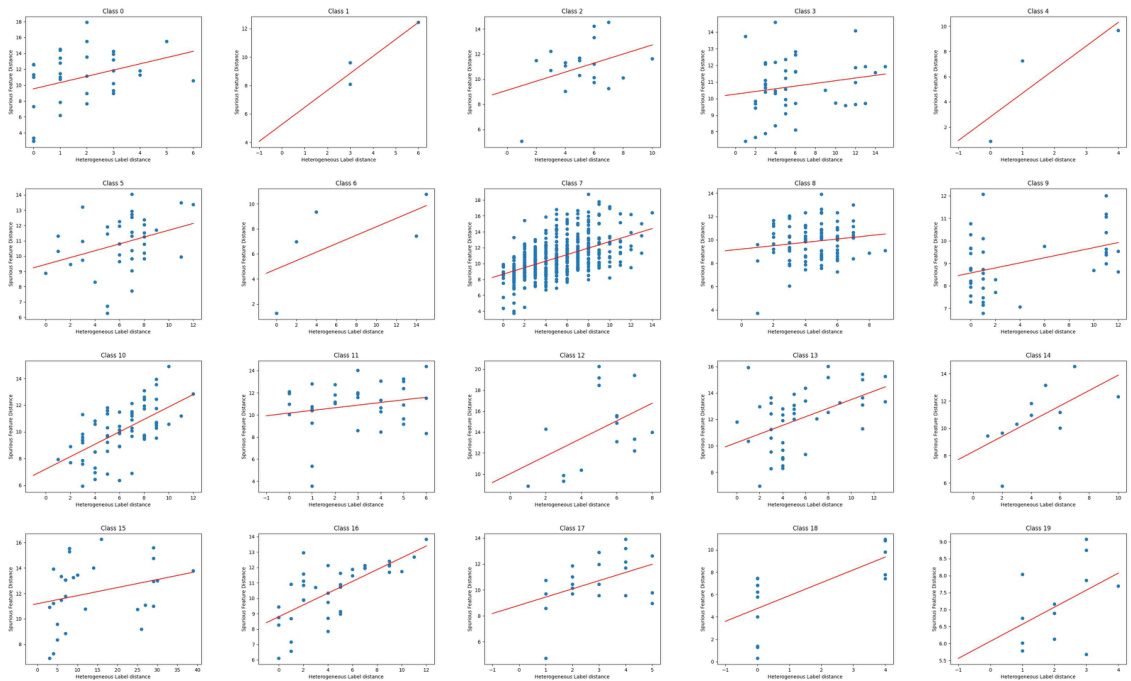
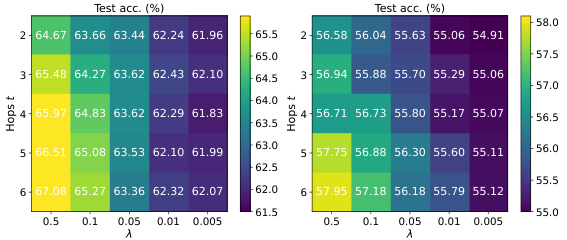
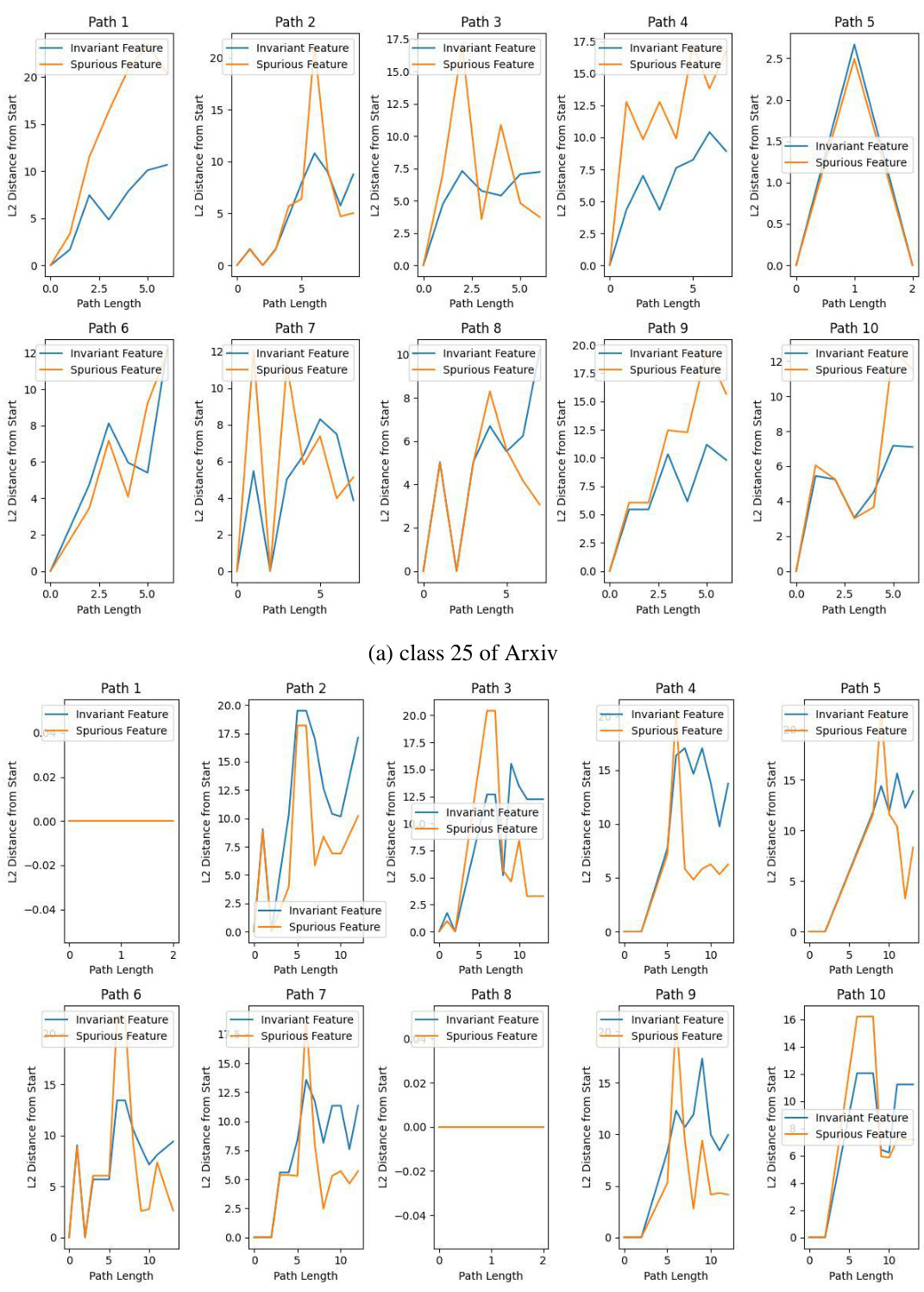
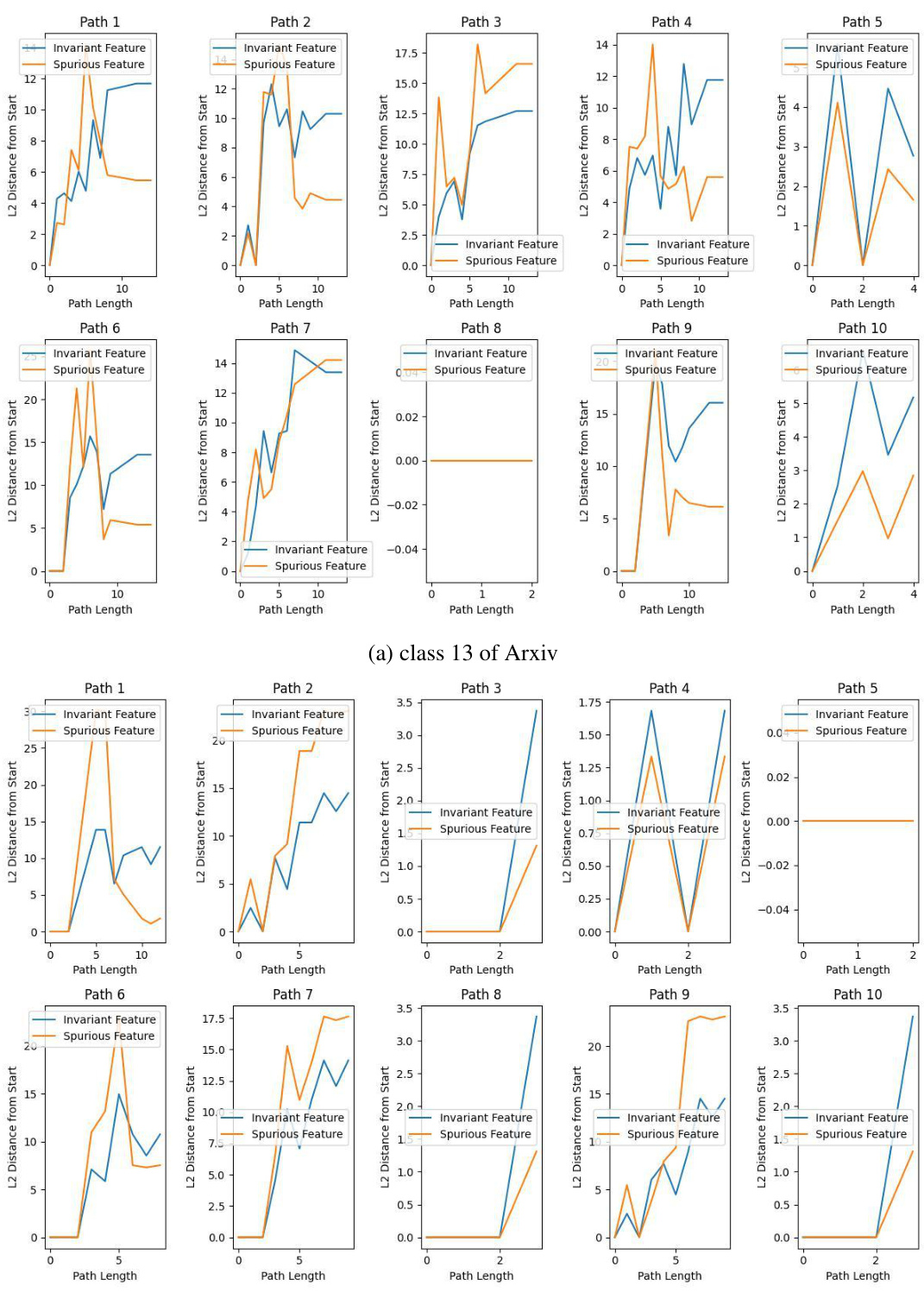
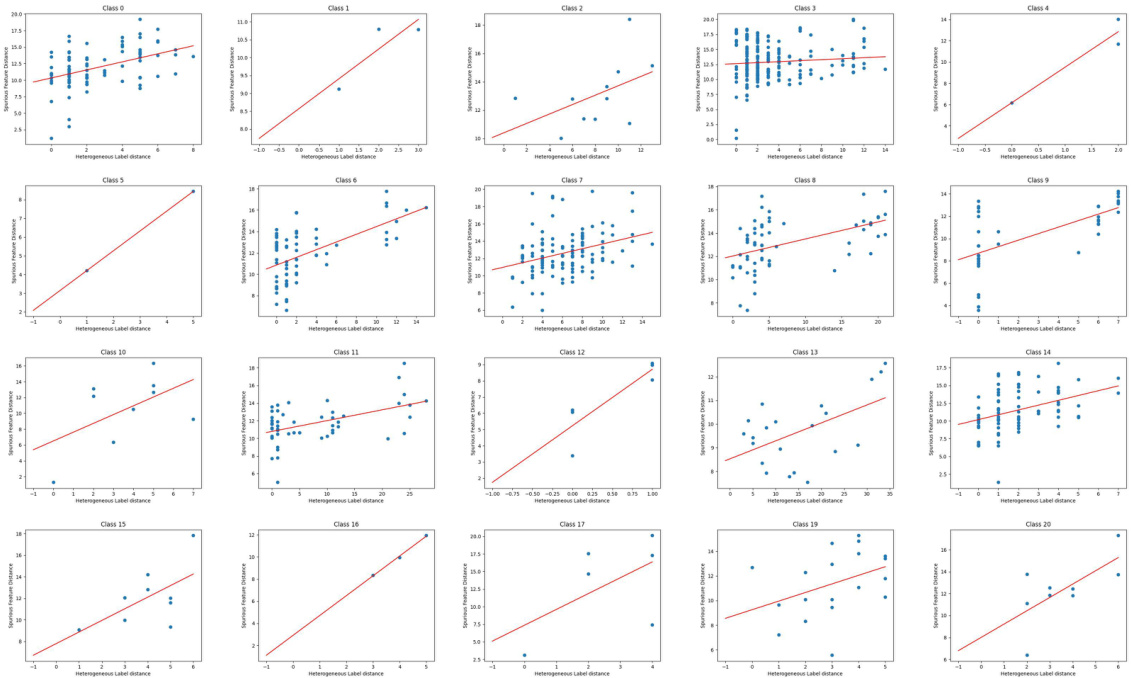
🔼 This figure shows the relationship between the distance of aggregated neighborhood representations and the distance of Heterophilic Neighborhood Label Distribution (HeteNLD) on the Cora dataset under covariate shift. Each subplot represents a different class, and each dot represents a node pair. A linear regression line is fitted to each plot, highlighting a clear positive correlation between the two variables, suggesting that HeteNLD can reflect spurious features on graphs.
read the caption
Figure 12: The relationship between the distance of the aggregated neighborhood representation and distance of HeteNLD on Cora word domain, covariate shift. Each sub-figure is a class, and each dot in the figure represents a node pair in the graph. The red line is obtained by linear regression. The positive correlation is clear.
🔼 This figure visualizes the results of the experiments conducted on a synthetic dataset to understand the effects of CIA and CIA-LRA on OOD generalization. The left panel shows the OOD test accuracy for both methods over training epochs. The middle panel displays the variance of the invariant representation, indicating the stability of learned features, and the right panel shows the norm of the spurious representation, illustrating the extent to which the model relies on irrelevant features. The results show that CIA-LRA maintains better performance and prevents the collapse of invariant representations which is observed with CIA as λ increases.
read the caption
Figure 3: Left: OOD test accuracy. Mid: the variance of the invariant representation. Right: the norm of the spurious representation. CIA and CIA-LRA use λ = 0.5 in this figure.
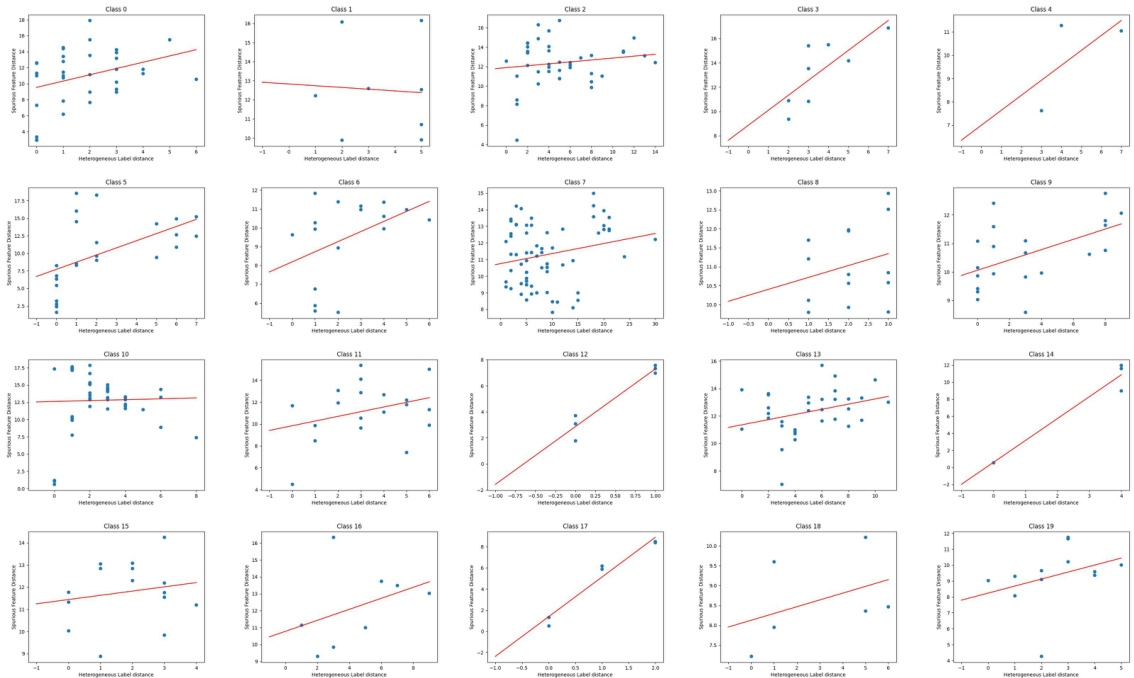
🔼 This figure visualizes the correlation between the distance of aggregated neighborhood representations and the Heterophilic Neighborhood Label Distribution (HeteNLD) discrepancy for each class in the Cora dataset under covariate shift. Each subplot represents a class, with each dot showing a node pair. A linear regression line is fitted to highlight the positive correlation. This suggests HeteNLD discrepancy effectively captures the difference in aggregated neighborhood representations.
read the caption
Figure 12: The relationship between the distance of the aggregated neighborhood representation and distance of HeteNLD on Cora word domain, covariate shift. Each sub-figure is a class, and each dot in the figure represents a node pair in the graph. The red line is obtained by linear regression. The positive correlation is clear.
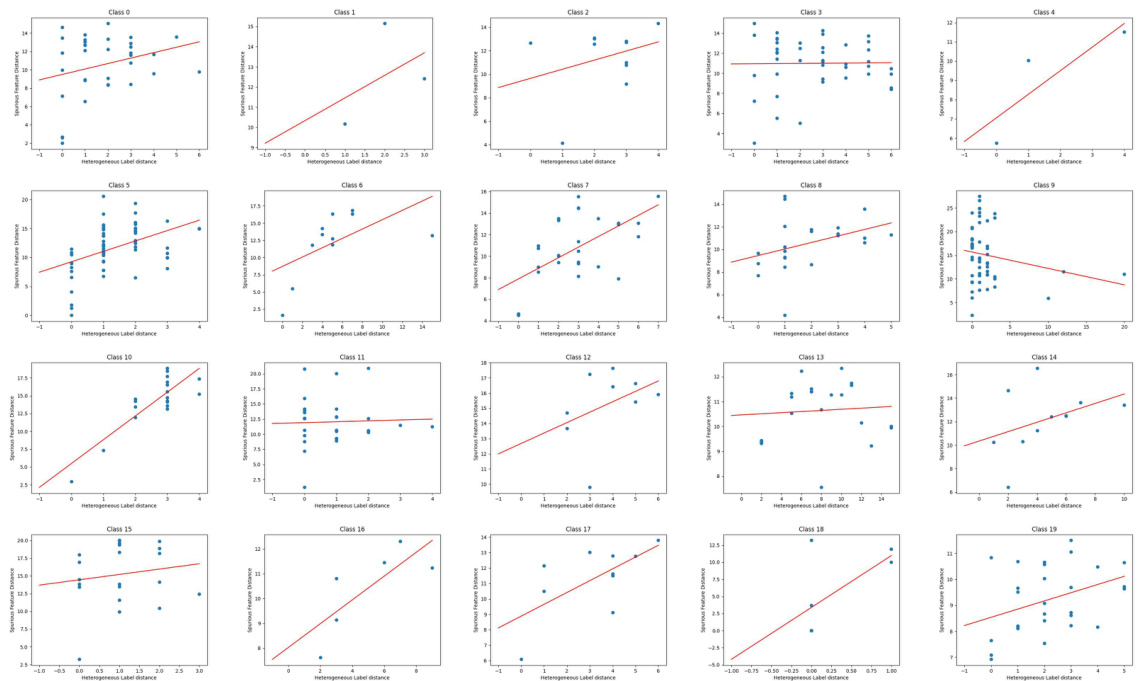
🔼 This figure shows the relationship between the distance of the aggregated neighborhood representation and the distance of HeteNLD on the Cora word domain under covariate shift. Each subplot represents a class, and each dot in a subplot represents a node pair in the graph. Linear regression lines are included. The positive correlation shown supports the claim that HeteNLD discrepancy reflects the distance of the aggregated neighborhood representation.
read the caption
Figure 12: The relationship between the distance of the aggregated neighborhood representation and distance of HeteNLD on Cora word domain, covariate shift. Each sub-figure is a class, and each dot in the figure represents a node pair in the graph. The red line is obtained by linear regression. The positive correlation is clear.
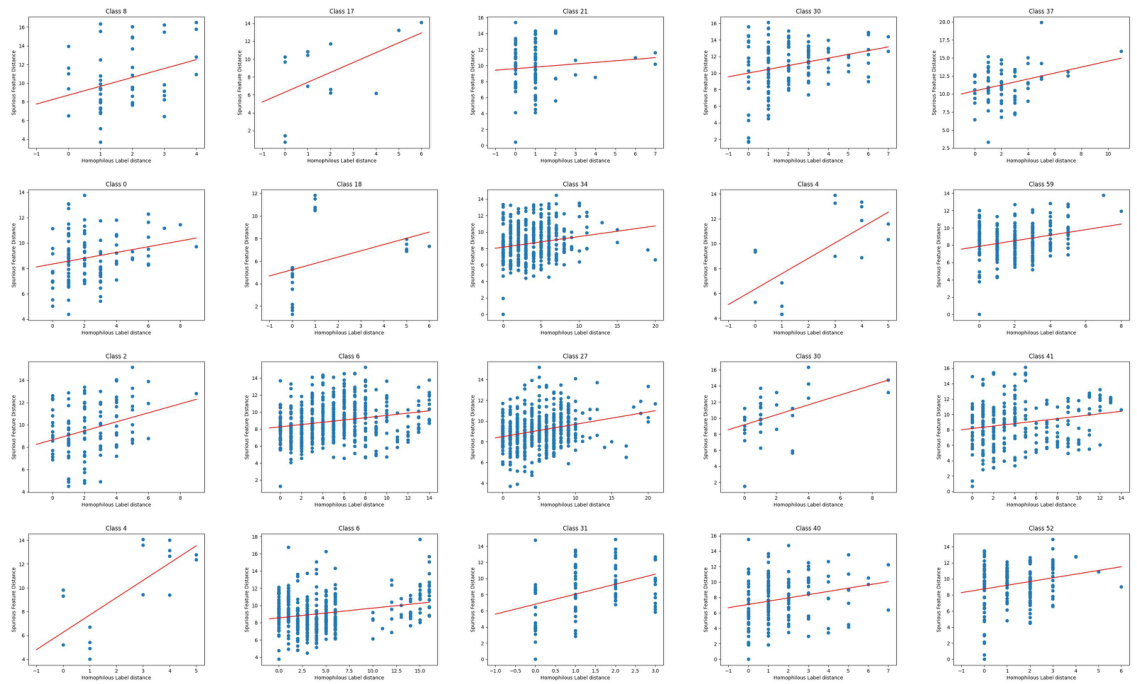
🔼 This figure shows the correlation between the distance of aggregated neighborhood representation and the HeteNLD (heterophilic neighborhood label distribution) distance for each class in the Cora dataset under covariate shift. Each point represents a pair of nodes with the same number of homophilic neighbors. The positive correlation suggests that HeteNLD distance effectively reflects the difference in aggregated neighborhood representations, supporting the use of HeteNLD in CIA-LRA for identifying node pairs with significant spurious feature differences for alignment.
read the caption
Figure 12: The relationship between the distance of the aggregated neighborhood representation and distance of HeteNLD on Cora word domain, covariate shift. Each sub-figure is a class, and each dot in the figure represents a node pair in the graph. The red line is obtained by linear regression. The positive correlation is clear.
More on tables
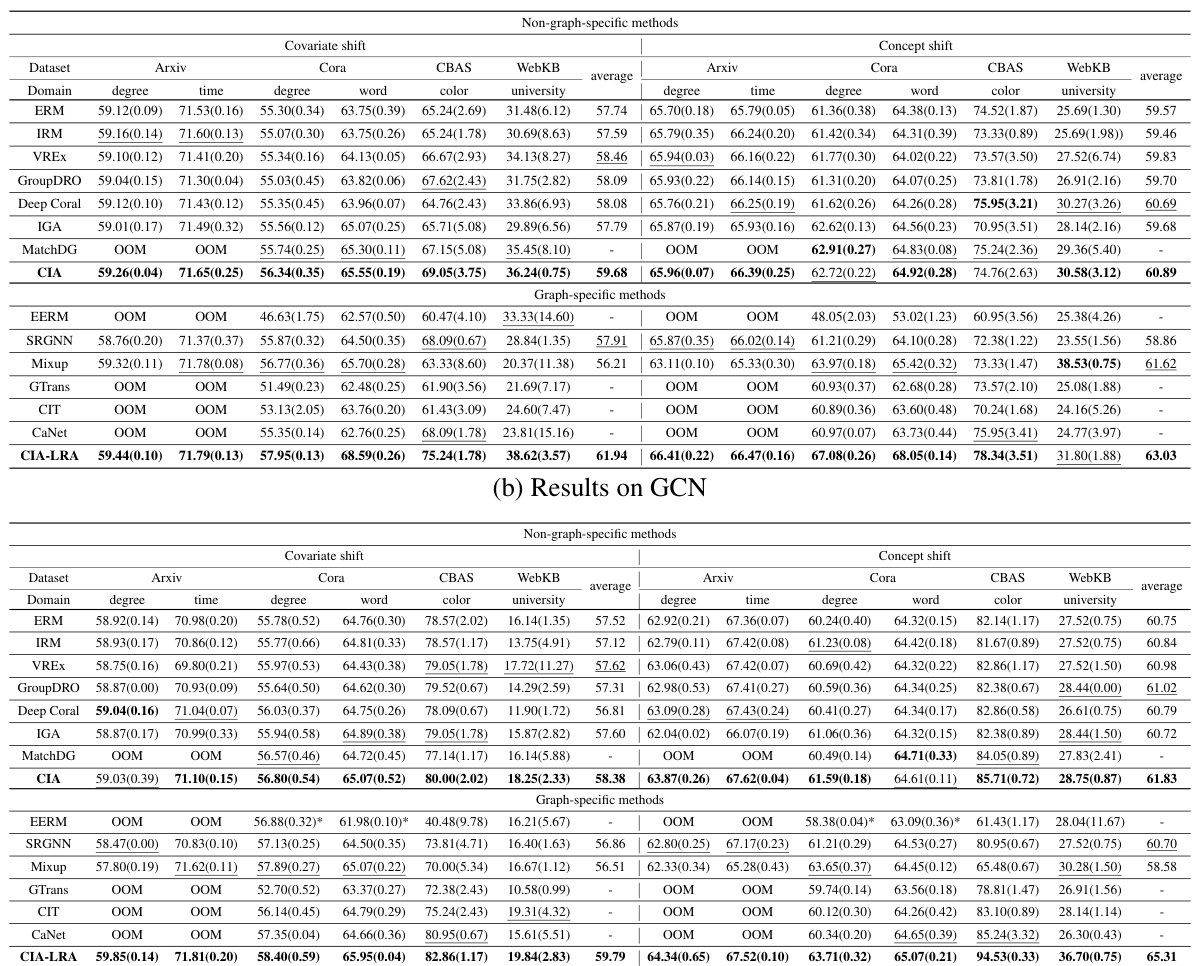
🔼 This table presents the OOD test accuracy results for various methods on the GAT and GCN models. The table is broken down by dataset (Arxiv, Cora, WebKB, CBAS), type of shift (covariate or concept), and specific split (degree, time, word, color, university). The best performing methods are highlighted, along with instances where the model ran out of memory (OOM). The table compares traditional invariant learning methods and graph-specific OOD methods.
read the caption
Table 2: OOD test accuracy (%). Our methods are marked in bold. The best and second-best results are shown in bold and underlined, respectively. The values in parentheses are standard deviations. 'OOM' denotes Out Of Memory. Results of EERM on Cora GCN marked by '*' are from Gui et al. [2022] since we got OOM during our running.
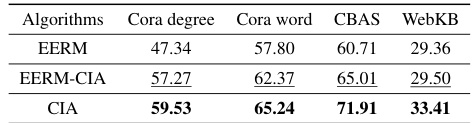
🔼 This table compares the performance of three different algorithms on four graph datasets: Cora degree, Cora word, CBAS, and WebKB. The algorithms are: EERM (an existing graph OOD method using VREx), EERM-CIA (EERM but replacing VREx with the proposed CIA method), and CIA (the proposed CIA method applied independently). The table shows that replacing VREx with CIA significantly improves performance across all four datasets, highlighting the effectiveness of CIA as an invariant learning objective.
read the caption
Table 3: By replacing VREx in EERM with CIA (marked as EERM-CIA), the performance is significantly improved.
🔼 This table presents the Out-of-Distribution (OOD) accuracy for several algorithms on various graph datasets. The algorithms tested include ERM (Empirical Risk Minimization), IRM (Invariant Risk Minimization), VREx (Variance-Risk Extrapolation), and the authors’ proposed methods CIA and CIA-LRA. The datasets are categorized into real-world datasets (Arxiv, Cora, and WebKB) and synthetic datasets (CBAS and a toy dataset). The results showcase the performance of each algorithm under two types of distributional shifts: covariate shift and concept shift. The ‘Toy’ column indicates the performance on a synthetic dataset designed to highlight the effects of spurious correlations.
read the caption
Table 1: Real-Cov./Con. are average OOD accuracy on the covariate/concept shift of Arxiv, Cora, CBAS, and WebKB. Toy denotes results on our toy synthetic graph OOD dataset.

🔼 This table presents the Out-Of-Distribution (OOD) accuracy results for several graph invariant learning methods on various datasets. The methods evaluated are Empirical Risk Minimization (ERM), Invariant Risk Minimization (IRM), Variance-Risk Extrapolation (VREx), and the authors’ proposed Cross-environment Intra-class Alignment (CIA) and CIA-LRA. The datasets include real-world graphs (Arxiv, Cora, WebKB) and a synthetic toy dataset designed to highlight spurious correlations. Results are shown for both covariate shift and concept shift scenarios, offering a comprehensive comparison of OOD generalization performance.
read the caption
Table 1: Real-Cov./Con. are average OOD accuracy on the covariate/concept shift of Arxiv, Cora, CBAS, and WebKB. Toy denotes results on our toy synthetic graph OOD dataset.

🔼 This table presents the Out-of-Distribution (OOD) accuracy results for several algorithms on four real-world graph datasets (Arxiv, Cora, CBAS, WebKB) and a synthetic toy dataset. The real-world datasets are evaluated under both covariate and concept shift scenarios. The algorithms include Empirical Risk Minimization (ERM), Invariant Risk Minimization (IRM), Variance-Risk Extrapolation (VREx), and the authors’ proposed methods, Cross-environment Intra-class Alignment (CIA) and Localized Reweighting Alignment (CIA-LRA). The results show that CIA and CIA-LRA significantly outperform the other methods, especially on the more challenging concept shift.
read the caption
Table 1: Real-Cov./Con. are average OOD accuracy on the covariate/concept shift of Arxiv, Cora, CBAS, and WebKB. Toy denotes results on our toy synthetic graph OOD dataset.

🔼 This table presents the out-of-distribution (OOD) generalization performance of several methods on various graph datasets. The datasets are categorized into real-world (Arxiv, Cora, CBAS, WebKB) and synthetic (Toy) datasets, with each dataset having covariate and concept shifts. The methods evaluated include ERM (Empirical Risk Minimization), IRM (Invariant Risk Minimization), VREx (Variance-Risk Extrapolation), and the authors’ proposed methods CIA and CIA-LRA. The results illustrate the OOD accuracy for each method across different datasets and shift types. The ‘Toy’ dataset was synthetically constructed to evaluate performance when spurious correlations exist between node features and labels.
read the caption
Table 1: Real-Cov./Con. are average OOD accuracy on the covariate/concept shift of Arxiv, Cora, CBAS, and WebKB. Toy denotes results on our toy synthetic graph OOD dataset.
Full paper#