TL;DR#
Many deep learning applications benefit from orthogonal transformations, but parameterizing orthogonal matrices efficiently is challenging. Existing methods like Cayley parametrization or matrix exponentials are computationally expensive or lack expressiveness, while block-diagonal approaches are too restrictive. Orthogonal fine-tuning (OFT) and Butterfly Orthogonal Fine-Tuning (BOFT) try to overcome these issues, but they still suffer from limitations in efficiency.
This paper introduces a new class of structured matrices called Group-and-Shuffle (GS) matrices. GS-matrices are parameterized efficiently using a product of block-diagonal matrices and permutations, offering a balance between density and low parameter count. The authors use GS-matrices to create a new method, GSOFT, for parameter-efficient orthogonal fine-tuning, demonstrating improvements in efficiency and performance in text-to-image diffusion models and language modeling. The GS approach is also extended to orthogonal convolutions.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel and efficient method for constructing dense orthogonal matrices, a crucial element in many deep learning tasks. This addresses limitations of previous methods, leading to improved parameter and computational efficiency in orthogonal fine-tuning. The work also extends to orthogonal convolutions. This improves various deep learning model’s efficiency and stability, opening avenues for further research in parameter-efficient training methods and efficient orthogonal operations in neural networks.
Visual Insights#
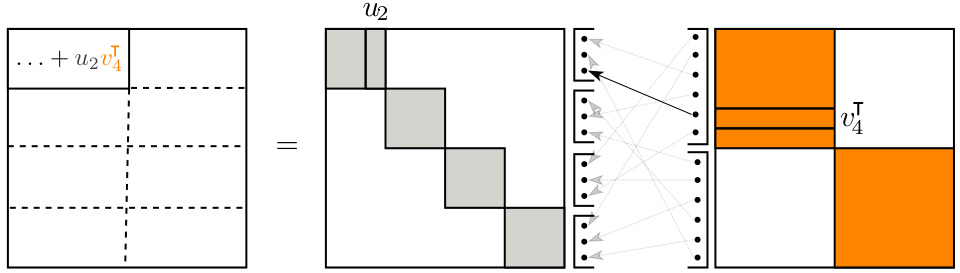
🔼 This figure illustrates Proposition 1, which states that matrices from the GS(I, P, I) class can be represented as block matrices with low-rank blocks. The ranks of these blocks are determined by the permutation matrix P. The illustration shows a GS(I, P, I) matrix with matrix R having 2 blocks and matrix L having 4 blocks, and visually demonstrates how the low-rank block structure arises from the interaction of the block-diagonal matrices and the permutation. Each colored block represents a low-rank block matrix, and it’s shown how the elements are combined based on the permutation.
read the caption
Figure 2: Illustration of Proposition 1 that provides block low-rank interpretation of GS(I, P, I) matrices. The matrix R contains 2 blocks and matrix L contains 4 blocks.

🔼 This table presents the results of the experiment conducted on the GLUE benchmark using the RoBERTa-base model. The experiment evaluated several different parameter-efficient fine-tuning methods, including the proposed GSOFT method. The table shows the performance of each method on various GLUE tasks, reported as Pearson correlation (STS-B), Matthews correlation (CoLA), and accuracy (other tasks). The ‘# Params’ column indicates the number of trainable parameters for each method.
read the caption
Table 1: Results on GLUE benchmark with RoBERTa-base model. We report Pearson correlation for STS-B, Matthew's correlation for CoLA and accuracy for other tasks. # Params denotes number of trainable parameters
In-depth insights#
Efficient Orthogonalization#
Efficient orthogonalization techniques are crucial for various machine learning applications, particularly in scenarios involving large-scale models. The core challenge lies in balancing computational efficiency with the preservation of orthogonality. Directly enforcing orthogonality through methods like the Cayley transform or matrix exponentiation can be computationally expensive, especially for high-dimensional matrices. Therefore, research focuses on structured orthogonalizations, leveraging sparsity or specific matrix structures (like block-diagonal or butterfly matrices) to reduce computational complexity. These approaches aim to approximate the true orthogonalization while maintaining a reasonable level of accuracy and stability during training. However, a trade-off often exists between the degree of structure imposed and the quality of the approximation. Finding optimal balance between the level of sparsity or structure and the resulting accuracy remains a central focus. Furthermore, effective initialization strategies and training methods are key to ensuring convergence and preventing training instabilities. Developing new structured matrix classes and exploring their properties for orthogonalization is an active area of research. The goal is to design efficient parametrizations that allow for accurate approximation of dense orthogonal matrices while requiring fewer parameters and computations.
GS-Matrix Properties#
The hypothetical section, ‘GS-Matrix Properties,’ would delve into the mathematical characteristics of the newly introduced Group-and-Shuffle (GS) matrices. This would likely include proofs demonstrating their key properties, such as the conditions under which they form dense matrices (unlike sparser alternatives), and importantly, when they guarantee orthogonality. The analysis would explore how the choice of permutation matrices and block-diagonal matrices influences these properties, potentially offering insights into optimal parameter choices for efficiency. Generalizations to higher-order GS-matrices would also be investigated, extending beyond the two-matrix product described earlier, along with a discussion of their computational complexity. The analysis might also compare GS-matrices with existing structured matrix classes like Monarch matrices, highlighting advantages and disadvantages in terms of density, orthogonality, and parameter efficiency. Finally, theoretical bounds on the rank of the GS-matrices would provide crucial insights into their expressiveness and potential limitations.
GSOFT Fine-Tuning#
The proposed GSOFT fine-tuning method offers a novel approach to parameter-efficient learning by leveraging a new class of structured matrices called GS-matrices. GSOFT generalizes and improves upon previous methods like OFT and BOFT, addressing their limitations in computational efficiency and expressiveness. The core innovation lies in the GS-matrix parametrization, which uses an alternating product of block-diagonal matrices and permutations to build dense orthogonal matrices. This structure allows GSOFT to achieve superior density compared to BOFT while requiring fewer matrices and parameters. Empirical validation across diverse domains, including text-to-image diffusion and language modeling, demonstrates GSOFT’s effectiveness in improving parameter and computational efficiency. Furthermore, the adaptation of GS-matrices for orthogonal convolutions showcases the versatility and potential of this approach in various neural network architectures. The GSOFT framework emerges as a highly promising advancement in parameter-efficient fine-tuning, offering a superior balance of efficiency and representational power.
Convolutions#
In the realm of deep learning, convolutions stand as a cornerstone operation, particularly within convolutional neural networks (CNNs). Their strength lies in their ability to efficiently extract features from input data by using a sliding window (kernel) that performs element-wise multiplications and summations. This process effectively detects patterns regardless of location. However, standard convolutions can suffer from computational limitations due to parameter count and processing time, especially in high-resolution images or video. This research delves into techniques for optimizing convolutions, focusing on improvements such as the development of efficient structured matrices like Group-and-Shuffle matrices for reducing parameter count and computational complexity. The exploration of orthogonal convolutions is also emphasized, which aims to maintain stability during training and potentially improve generalization. The study highlights the importance of efficient orthogonal parametrizations to enhance performance and mitigate computational overheads in existing orthogonal fine-tuning and convolution methods.
Future Works#
The ‘Future Works’ section of this research paper could explore several promising avenues. Extending the GS-matrix framework to handle non-square matrices would broaden its applicability to a wider range of deep learning tasks. Investigating the theoretical properties of GS-matrices in the context of orthogonal convolutional layers is crucial to understand their behavior and optimize their performance. Empirical evaluation on a broader range of architectures and datasets beyond those presented would strengthen the claims of generalizability and efficiency. Furthermore, a deeper analysis of the relationship between GS-matrices and other structured orthogonal parametrizations (like BOFT and Monarch matrices) could lead to a unified understanding and potentially more efficient methods. Finally, exploring the application of GS-matrices to other parameter-efficient fine-tuning techniques like prompt tuning and adapter methods could unlock new possibilities for efficient model adaptation.
More visual insights#
More on figures
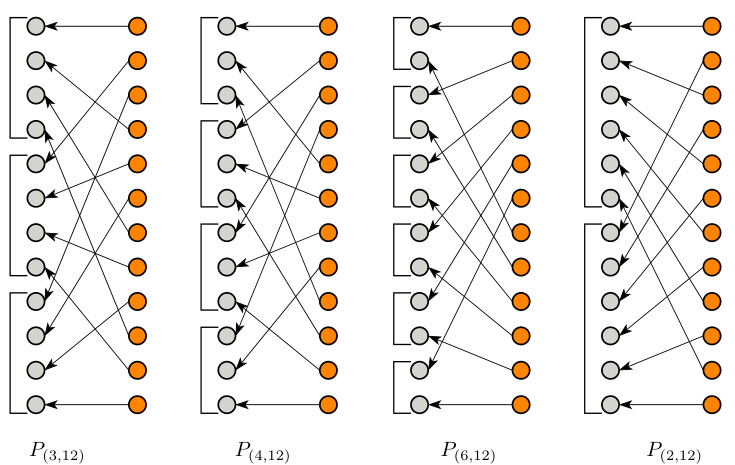
🔼 This figure illustrates four different permutation matrices, denoted as P(k, 12), where k takes on the values 3, 4, 6, and 2. Each matrix represents a permutation of 12 elements. The visual representation uses nodes and arrows to depict how each element is mapped to its new position after the permutation. The figure helps to understand the effect of different permutation choices within the GS-matrix class, which is central to the paper’s method for constructing efficient orthogonal matrices.
read the caption
Figure 3: Illustration of P(k,12) permutations for k ∈ {3,4,6,2}.

🔼 This figure shows the results of subject-driven generation for different methods after 3000 training iterations. Each row represents a different concept (a vase, a clock, and a dog). The first column shows the original concept image. The subsequent columns demonstrate generated images using LoRA, BOFT, GSOFT, and Double GSOFT, showcasing the effects of each method on generating variations of the concept while maintaining fidelity to textual prompts.
read the caption
Figure 4: Subject-driven generation visual results on 3000 training iterations.

🔼 This figure illustrates how information flows through a layered block structure in the GS-matrix. Each node represents an element, and the connections between nodes show how information is transferred. The number of connections from one layer to the next (b) determines the density and structure of the resulting matrix. It helps visualize the concept of ‘group-and-shuffle’ as the information passes through multiple layers of block diagonal matrices and permutations. This specific structure is relevant to demonstrating the theorem related to achieving a dense matrix representation using GS matrices.
read the caption
Figure 5: Demonstration of information transition through a block structure. Each node is connected to exactly b consecutive nodes from the next level.
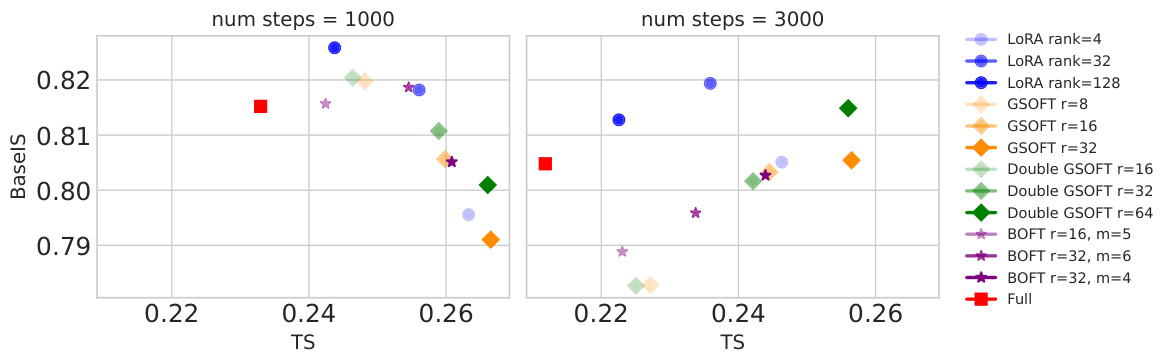
🔼 This figure shows a graphical representation of the image similarity (IS) and text similarity (TS) metrics for various methods on the subject-driven generation task, comparing results after 1000 and 3000 training iterations. It illustrates the tradeoff between the two metrics for different models (LoRA, GSOFT, Double GSOFT, BOFT, and a full model) and parameters.
read the caption
Figure 6: Image and text similarity visualisation for different methods on subject-driven generation.

🔼 This figure shows the results of subject-driven image generation using different methods after 3000 training iterations. The top row displays the original concept image and the following rows show images generated using various methods, including LORA, BOFT, GSOFT, and Double GSOFT. Each concept is represented by several rows, showing the different generated images for each method. The caption is intentionally short as the figure itself shows the results.
read the caption
Figure 4: Subject-driven generation visual results on 3000 training iterations.

🔼 This figure shows the results of subject-driven generation using different methods after 3000 training iterations. It compares the image generation quality of several approaches: LoRA (with different rank values), BOFT (with different rank and number of matrices m), GSOFT, and Double GSOFT. Each row presents a different concept, while the columns showcase images generated with each method. The images illustrate how well each method generates images corresponding to a specific textual description, considering both the concept’s fidelity and the adherence to the prompt.
read the caption
Figure 4: Subject-driven generation visual results on 3000 training iterations.
More on tables
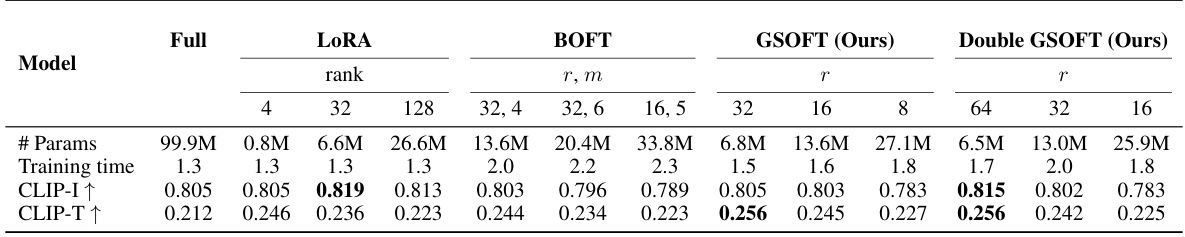
🔼 This table presents the results of subject-driven generation experiments using different parameter-efficient fine-tuning methods. It shows the number of trainable parameters (# Params), training time in hours on a single V100 GPU, CLIP image similarity (CLIP-I↑), and CLIP text similarity (CLIP-T↑) for various models: Full model (all parameters trained), LoRA, BOFT, GSOFT, and Double GSOFT. The table helps in comparing the efficiency and effectiveness of different methods for this task.
read the caption
Table 2: Results on subject-driven generation. # Params denotes the number of training parameters in each parametrization. Training time is computed for 3000 iterations on a single GPU V100 in hours.
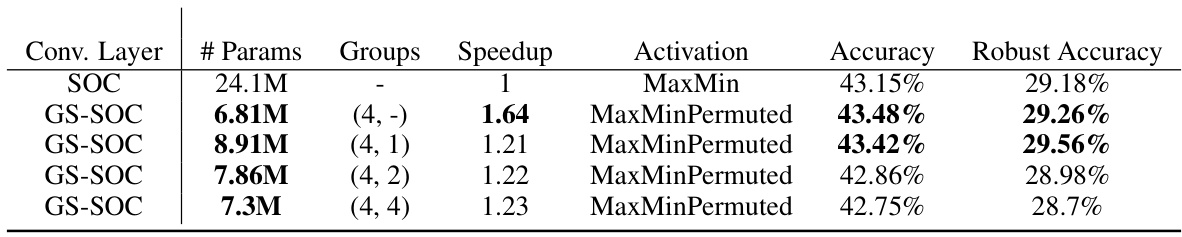
🔼 This table presents the results of training a LipConvnet-15 architecture on the CIFAR-100 dataset. It compares the performance of standard skew orthogonal convolutions (SOC) with the proposed GS orthogonal convolutions (GS-SOC). The table shows the number of parameters, the number of groups used in the grouped convolutional layers, speedup factor compared to SOC, the activation function used, the accuracy, and robust accuracy achieved by each model. Different configurations of GS-SOC are evaluated by varying the number of groups in the two grouped convolutional layers and using different activation functions and permutation types within the ChShuffle operator.
read the caption
Table 3: Results of training LipConvnet-15 architecture on CIFAR-100. (a, b) in “Groups” column denotes number of groups in two grouped exponential convolutions (with kernel sizes 3 and 1). (a, -) corresponds to only one GS orthogonal convolutional layer. Before each grouped layer with k groups use a ChShuffle operator.
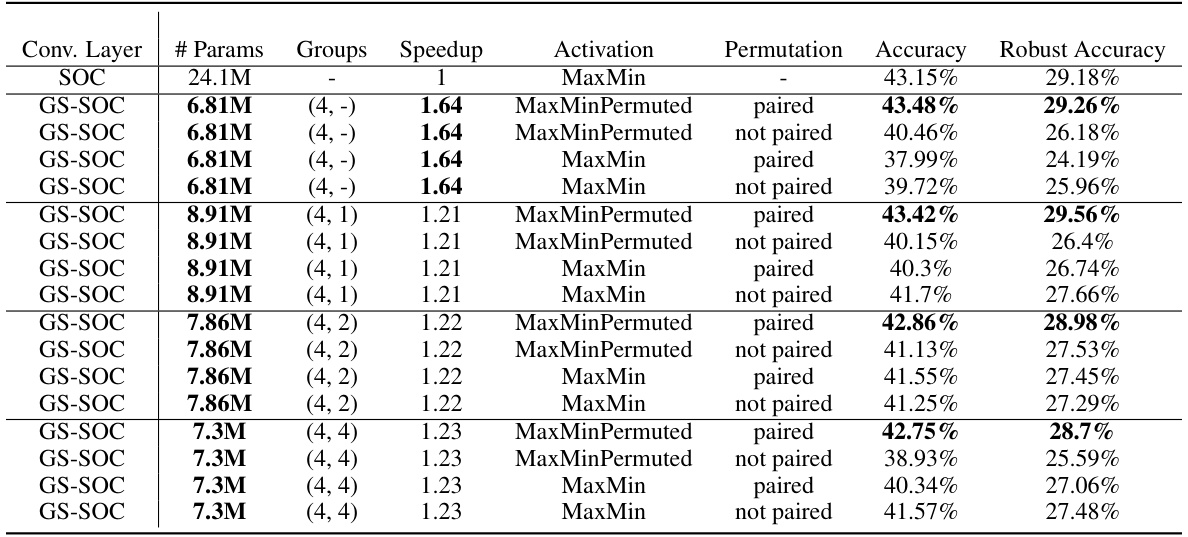
🔼 This table presents the results of training a LipConvnet-15 architecture on the CIFAR-100 dataset. It compares different configurations of the GS-orthogonal convolution layer, varying the number of groups, the speedup achieved, the activation function used, the permutation method applied, and the resulting accuracy and robust accuracy. The table helps to analyze the impact of various design choices on model performance and efficiency.
read the caption
Table 3: Results of training LipConvnet-15 architecture on CIFAR-100. (a, b) in “Groups” column denotes number of groups in two grouped exponential convolutions (with kernel sizes 3 and 1). (a, -) corresponds to only one GS orthogonal convolutional layer. Before each grouped layer with k groups use a ChShuffle operator.
Full paper#



















