TL;DR#
Nearest neighbor search (NNS) is a fundamental problem across many fields. A common approach uses navigable graphs: sparse data structures where greedy routing efficiently finds nearest neighbors. However, constructing truly sparse, navigable graphs in high-dimensional spaces is challenging. Existing methods often lack theoretical guarantees on performance or sparsity. Prior work had not established tight bounds on the sparsity of such graphs.
This paper addresses this gap. The authors introduce a novel, efficient algorithm for creating navigable graphs with average degree O(nlogn), regardless of the dimensionality of the data or distance metric. Importantly, they also provide a nearly matching lower bound, proving that for random point sets, even in just O(log n) dimensions, there exists no navigable graph with significantly lower degree. This work offers a comprehensive theoretical understanding of the limits of sparse navigable graphs in high dimensions, offering guidance for future NNS algorithm design.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between the practical use of navigable graphs in high-dimensional nearest neighbor search and the theoretical understanding of their limitations. It provides efficient graph construction methods with proven performance bounds, directly addressing a key challenge in this field. This work opens avenues for improved algorithms and a deeper understanding of the trade-offs between graph sparsity and search efficiency in high dimensions. The sharp lower bounds offer valuable insights for future algorithm design, preventing the pursuit of overly optimistic sparsity goals.
Visual Insights#
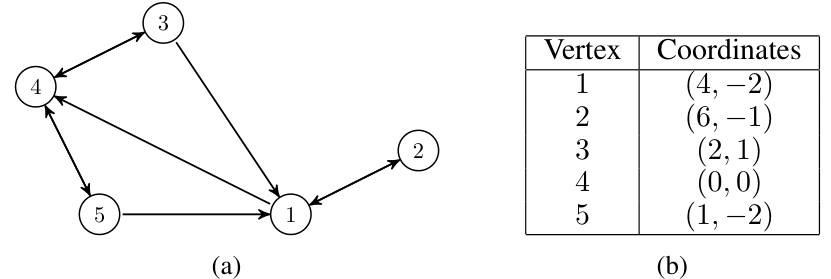
🔼 This figure shows a directed graph with 5 nodes and several edges. The direction of the edges is indicated by arrows. A double-ended arrow signifies that an edge exists in both directions between the two nodes. The caption indicates that this specific graph is an example of a navigable graph, which can be verified using another figure (Figure 2 in the paper) that provides additional information needed for verification. Navigability, in this context, relates to a greedy routing strategy used for nearest neighbor search.
read the caption
Figure 1: Example of a navigable graph G = (V, E) on 5 nodes. A double arrow indicates that both (i, j) ∈ E and (j, i) ∈ E. We can check that G is navigable by referring to Figure 2.

🔼 This table shows the distance-based permutations for the dataset shown in Figure 1. For each node, it lists its neighbors in increasing order of distance. This ordering is used to demonstrate the navigability property of the graph in Figure 1. If a graph is navigable, there will be an edge from each node in the list to a prior node that is closer to the target node (the query).
read the caption
Figure 2: Distance-based permutation for the data set in Figure 1.
Full paper#


















