TL;DR#
Stackelberg prediction games (SPGs) model strategic interactions in machine learning, but are computationally hard to solve. A recent method called SCLS (spherically constrained least squares) offers a solution but lacks theoretical backing on its error. This paper addresses the issue by providing a rigorous theoretical analysis of the SCLS method’s accuracy. The authors successfully prove that the error converges to zero with increasing data, confirming SCLS’s reliability.
The research team used the Convex Gaussian Min-max Theorem (CGMT) to simplify the problem. They then reframed the estimation error as a primary optimization problem, which they further transformed into a simpler auxiliary optimization problem for analysis. This analysis strengthens the theoretical framework of the SCLS method and verifies the method’s effectiveness through experiments, which show an excellent match between theoretical predictions and observed results.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides the first theoretical error analysis for the SCLS method, a state-of-the-art algorithm for solving Stackelberg prediction games. This addresses a significant gap in the literature and validates the reliability of the SCLS method for large-scale applications. The theoretical framework developed here also opens avenues for error analysis in other machine learning algorithms, impacting various fields like intrusion detection and spam filtering.
Visual Insights#

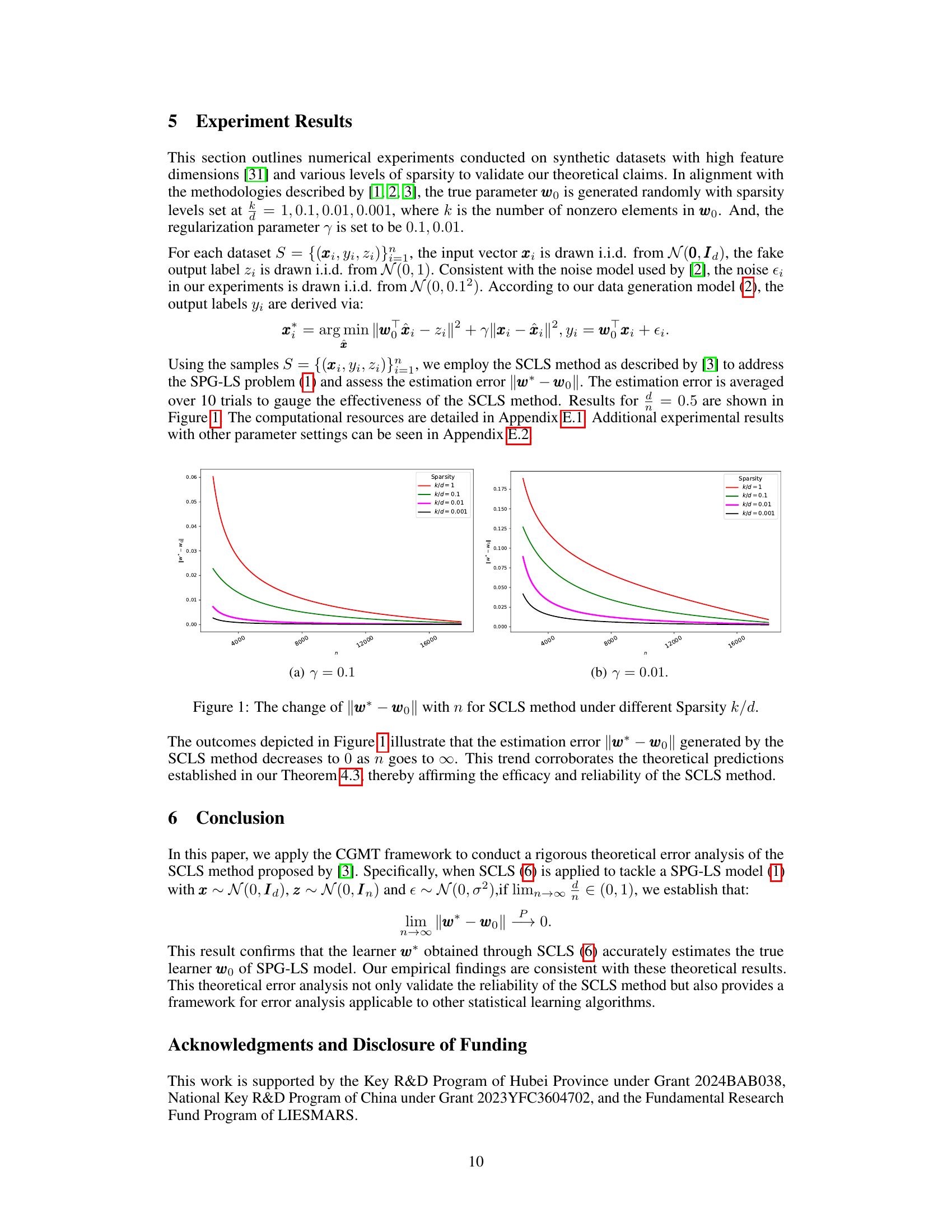
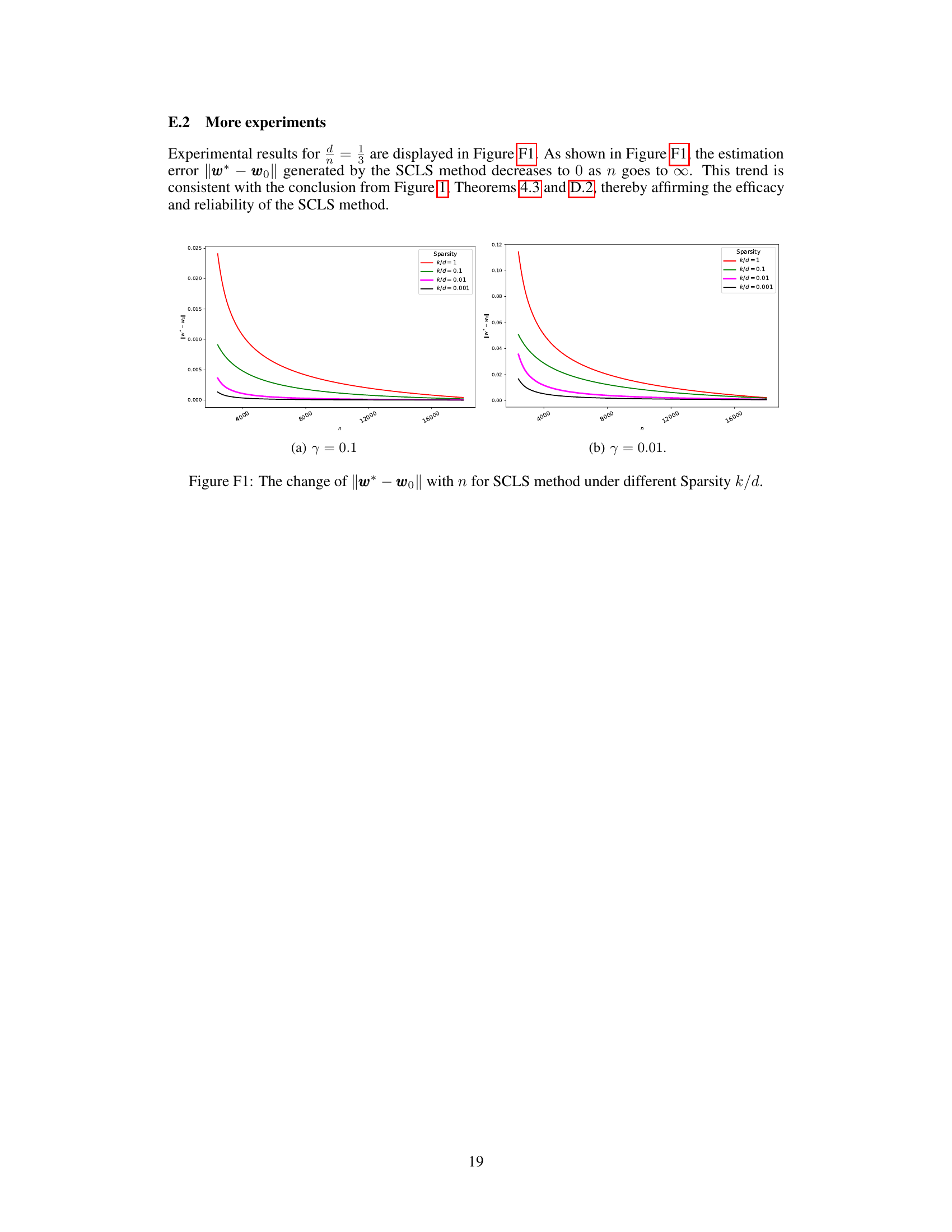
🔼 This figure displays the estimation error ||w* - w0||, illustrating the difference between the learner obtained using the SCLS method (w*) and the true learner (w0), plotted against the number of samples (n) for different sparsity levels (k/d). It showcases how the estimation error decreases as the sample size increases, with different lines representing various sparsity levels. This graph empirically validates the theoretical finding that the error converges to zero as n approaches infinity.
read the caption
Figure 1: The change of ||w* – wo|| with n for SCLS method under different Sparsity k/d.
Full paper#