TL;DR#
Deep Neural Networks (DNNs) are susceptible to weight errors, impacting accuracy. Error-Correcting Output Codes (ECOCs), particularly the simple one-hot encoding, are commonly used but often lack robustness. Existing studies experimentally showed that better ECOCs exist but lacked theoretical foundation.
This paper uses the Neural Tangent Kernel (NTK) framework to analyze ECOCs’ effectiveness. It demonstrates that ECOCs alter decoding metrics and reveals a threshold for error tolerance. By balancing codeword orthogonality and distance, the paper proposes new ECOC construction methods. Extensive experiments across various datasets and DNN models confirm the superior performance of the proposed methods over existing ECOCs.
Key Takeaways#
Why does it matter?#
This paper is crucial because it provides theoretical explanations for the effectiveness of ECOCs in DNNs, a widely used technique often applied without a deep understanding. The research offers design guidance for creating optimized ECOCs, significantly improving DNN robustness against weight errors. This is highly relevant given the increasing use of DNNs in resource-constrained environments and the growing focus on their reliability.
Visual Insights#
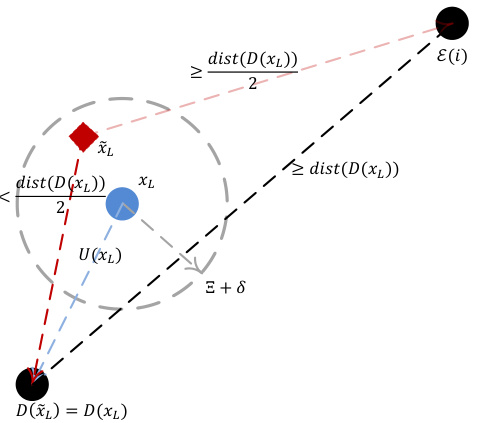
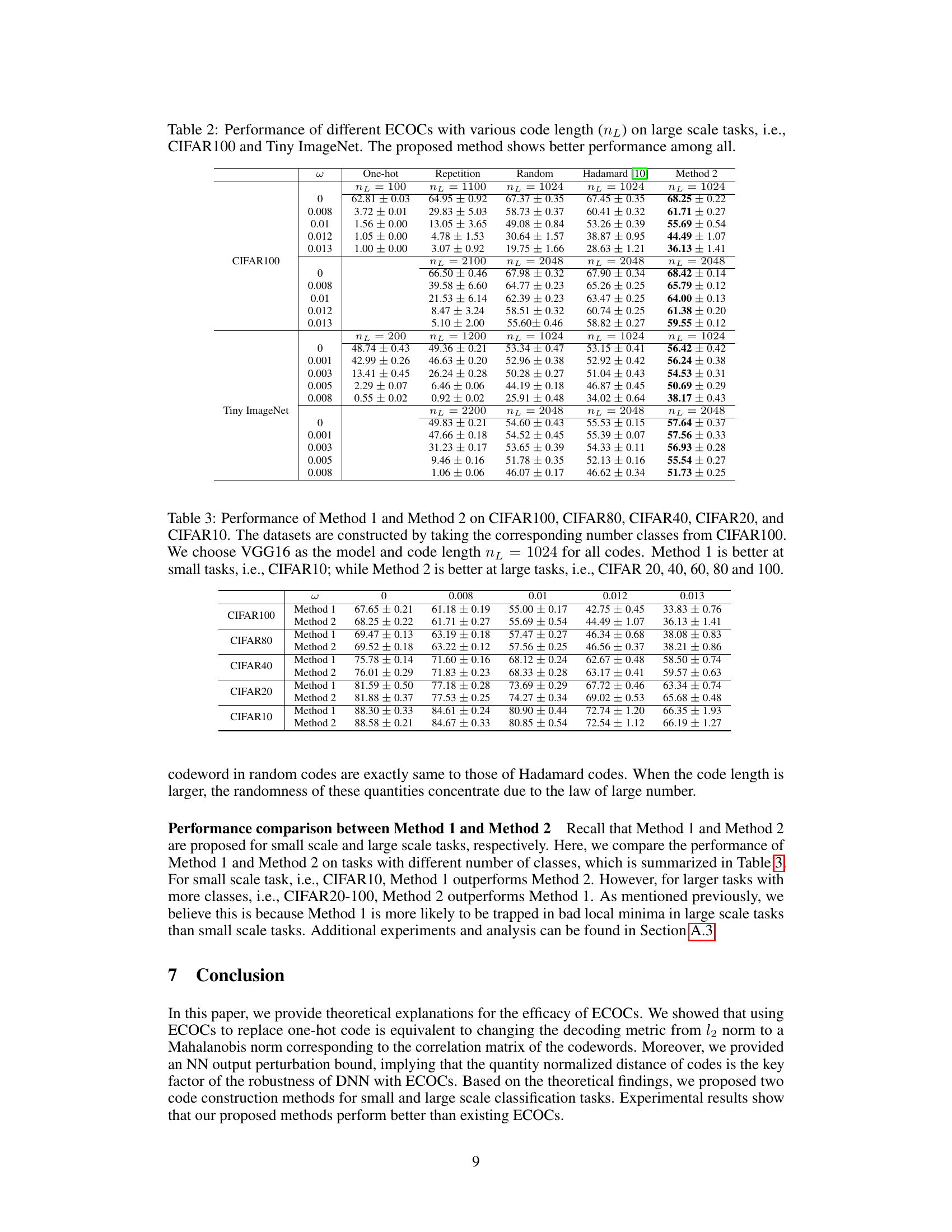
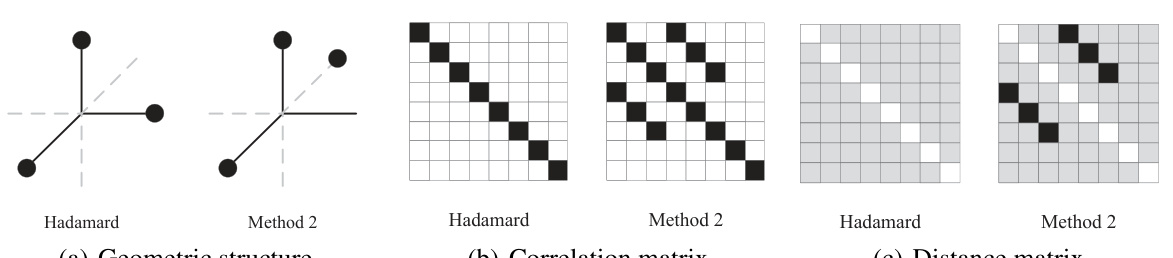
🔼 This figure provides a geometric illustration of Corollary 1, which establishes a threshold for the robustness of DNNs using ECOCs in the presence of weight errors. The red diamond represents the perturbed output (\tilde{x}_L), while the blue circle represents the clean output (x_L) with radius (Ξ + δ) that bounds the perturbation. The black dots represent codewords. The distance between the clean output and its nearest codeword (D(x_L)) (bottom left) is denoted by (U(x_L)). If the distance between (\tilde{x}_L) and (D(x_L)) is smaller than the distance between (\tilde{x}_L) and any other codeword, (D(\tilde{x}_L) = D(x_L)). The normalized distance between codewords is shown as well.
read the caption
Figure 1: An illustration for Corollary 1.
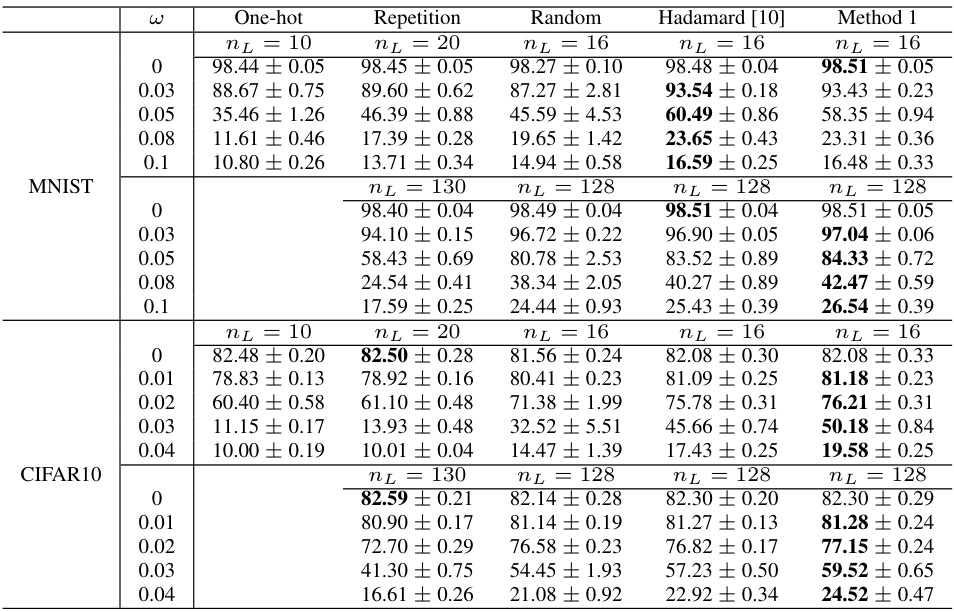
🔼 This table presents the performance comparison of different ECOC methods (One-hot, Repetition, Random, Hadamard, and the proposed Method 1) on two small-scale datasets: MNIST and CIFAR10. The performance is evaluated under varying levels of weight-errors (ω) and different code lengths (nL or η₁). The results show the accuracy of each method under clean conditions (ω=0) and various levels of Gaussian noise added to the weights during inference. The proposed Method 1 generally outperforms other methods, especially when weight errors are present.
read the caption
Table 1: Performance of different ECOCs with various code length (nL) on small scale tasks, i.e., MNIST and CIFAR10. The proposed method achieves better performance in the presence of weight-errors.
In-depth insights#
ECOC Robustness#
The concept of “ECOC Robustness” centers on enhancing the resilience of Error Correcting Output Codes (ECOCs) in the face of errors, particularly within the context of neural networks. Traditional ECOCs, like one-hot encoding, while simple, lack robustness against weight errors that can arise from hardware imperfections or noisy training data. The core idea is to design ECOCs that can still produce accurate classifications even when some of the underlying network weights are perturbed. This involves exploring different code structures and decoding metrics. One key finding frequently highlighted is the trade-off between codeword orthogonality (which improves clean accuracy) and code distance (crucial for error correction). Optimal ECOCs aim to strike a balance between these competing factors. Theoretical analyses, often leveraging Neural Tangent Kernels (NTKs), provide insights into the effect of code design on DNN performance with and without weight-errors. The application of robust ECOCs is not limited to specific neural network architectures; rather, they offer a general approach to improve the robustness of multi-class classifiers against various forms of noise and uncertainty. Ultimately, “ECOC Robustness” aims to enhance reliability and stability, making neural networks less susceptible to errors.
NTK Analysis#
The heading ‘NTK Analysis’ suggests a section dedicated to exploring the properties of neural tangent kernels (NTKs) within the context of the research paper. An in-depth NTK analysis would likely involve several key aspects. First, it would probably delve into the theoretical underpinnings of NTKs, potentially discussing their connection to infinite-width neural networks and their role as a tool for understanding the learning dynamics of these networks. A key focus would likely be on leveraging NTKs to analyze the impact of weight errors. The analysis might involve deriving bounds on the perturbation of network outputs due to weight errors, using NTK theory to quantify the robustness of the system. This could potentially lead to novel insights on the relationship between the design of the error-correcting output codes (ECOCs) and their effectiveness in mitigating the impact of these weight errors. Furthermore, the analysis may investigate how different decoding metrics (like the L2 distance and Mahalanobis distance) relate to the choice of ECOC and the resulting robustness of the neural network using NTK as an analytical framework. The authors could also analyze the convergence and generalization properties in the presence of weight errors. In summary, a comprehensive NTK analysis would provide a theoretical framework to understand and potentially improve the robustness of neural networks against weight-errors.
Code Design#
The effectiveness of Error Correcting Output Codes (ECOCs) in bolstering the robustness of neural networks hinges critically on thoughtful code design. Optimal ECOC design aims to balance two competing objectives: maximizing codeword orthogonality to enhance clean model performance and widening inter-codeword distances to improve resilience against weight errors. The paper introduces a novel framework using the Neural Tangent Kernel (NTK) to theoretically ground this design process. The NTK analysis reveals a threshold based on normalized codeword distances and weight-error magnitudes, beyond which DNN predictions remain impervious to these errors. This informs two distinct ECOC construction methods: one tailored to smaller datasets, leveraging direct optimization to find codes that approximate orthogonality while maintaining distance; and a second for larger datasets that leverages Hadamard codes and strategically introduces complement pairs to fine-tune the balance between orthogonality and distance. Experimental validations across multiple DNN architectures and datasets demonstrate the superior performance of these novel ECOC designs compared to existing approaches, empirically supporting the theoretical findings and offering valuable design principles for future work in robust neural network architectures.
Empirical Results#
An Empirical Results section in a research paper should present a detailed and thorough evaluation of the proposed method. It needs to go beyond simply reporting numbers; it should provide a nuanced interpretation of the findings. This involves comparing results across various datasets, baselines, and parameter settings. Visualizations such as graphs and tables are crucial, making trends and comparisons easy to grasp. The discussion should acknowledge limitations and potential biases, especially when generalizing findings. For instance, if a method performs well only under specific conditions, the limitations should be clearly articulated. A robust empirical analysis must also address statistical significance, demonstrating that observed differences are unlikely due to random chance. Furthermore, a discussion connecting empirical observations to theoretical claims (if any) within the paper should be included. This integration will create a more comprehensive understanding. Ultimately, the goal of the Empirical Results section is to convincingly demonstrate the effectiveness, robustness, and potential of the proposed method while maintaining transparency and intellectual honesty.
Future Work#
The ‘Future Work’ section of this research paper presents several promising avenues for extending this research. One key area is to explore the application of the proposed ECOC construction methods to a broader range of DNN architectures and datasets. This would strengthen the generalizability of the findings and provide more compelling evidence of the methods’ effectiveness. Another crucial aspect would be to conduct a more in-depth analysis of the interplay between code orthogonality, code distance, and DNN architecture. This deeper understanding could lead to more sophisticated ECOC designs optimized for specific DNN types and tasks. Furthermore, investigating the impact of different decoding metrics and loss functions on the robustness of ECOC-DNNs is vital. This could potentially reveal new ways to further enhance the effectiveness of the error correction capabilities. Finally, it would be beneficial to investigate the applicability of this work to other types of network errors, not just weight-errors. This would expand the scope of the research and make the proposed techniques more practical and valuable.
More visual insights#
More on figures
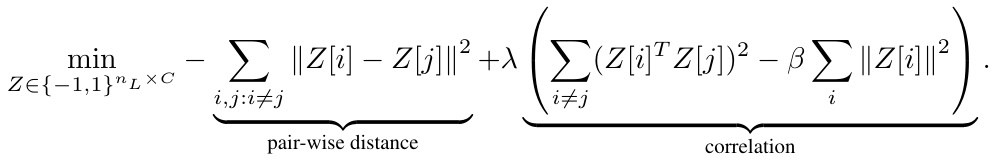
🔼 This figure provides a geometric illustration for Corollary 1, which establishes a threshold condition for the robustness of DNNs using ECOCs against weight errors. The red diamond represents the perturbed output (with weight errors), while the blue dot represents the clean output (without weight errors). The black dots represent the codewords. The corollary states that if the distance between the clean output and its nearest codeword (bottom left) is smaller than a threshold (determined by the normalized distance between codewords, DNN architecture and weight error scale) plus the perturbation of the output due to weight errors, then the DNN’s prediction remains unaffected by weight-errors, despite the perturbation of the output. If the distance is greater than this threshold, the perturbed output might be decoded to a different codeword.
read the caption
Figure 1: An illustration for Corollary 1.
🔼 This figure provides a geometric explanation of Corollary 1, which establishes a threshold for the robustness of a DNN using ECOCs against weight errors. The red diamond represents the perturbed output, the blue dot represents the clean output, and the black dots represent the codewords. If the distance between the perturbed output and its closest codeword (black dot at bottom left) is smaller than the distance to other codewords, then the DNN makes predictions as if it were free of weight errors.
read the caption
Figure 1: An illustration for Corollary 1.
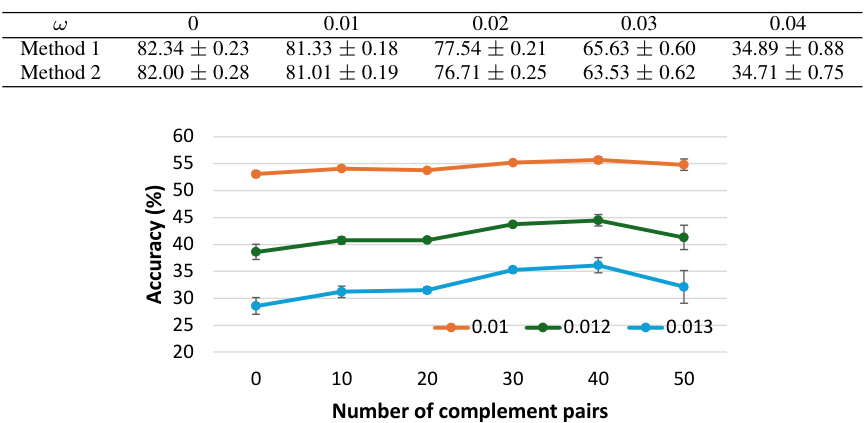
🔼 This figure shows the accuracy comparison of different ECOCs constructed by Method 2 with varying numbers of complement pairs. The x-axis represents the number of complement pairs, and the y-axis represents the accuracy. Three lines represent the results with different noise levels (weight errors). The figure demonstrates that increasing the number of complement pairs increases both the average distance between codewords and the correlation among them. A balance is found with 40 complement pairs, achieving optimal accuracy by finding the best trade-off between these two factors. The experiment is performed on the CIFAR100 dataset using the VGG-16 model and a code length of 1024.
read the caption
Figure 3: Accuracy comparisons for different number of complement pairs included when constructing ECOC with Method 2. Including more complement pairs means higher average distance while larger correlation. 0 complement pair is Hadamard code. In this plot, 40 complement pairs achieve the best trade-off between distance and correlation. The dataset, model and code length are CIFAR100, VGG-16 and 1024.
More on tables

🔼 This table presents the performance comparison of different ECOCs (Error Correcting Output Codes) on two large-scale image classification datasets: CIFAR-100 and Tiny ImageNet. The performance is evaluated under varying levels of weight-error (noise added to the model weights during inference), represented by the ω values. Different ECOC methods are compared: One-hot, Repetition, Random, Hadamard, and the proposed Method 2. The table shows that the proposed Method 2 generally outperforms other methods in terms of accuracy, especially when there is significant weight error.
read the caption
Table 2: Performance of different ECOCs with various code length (nL) on large scale tasks, i.e., CIFAR100 and Tiny ImageNet. The proposed method shows better performance among all.
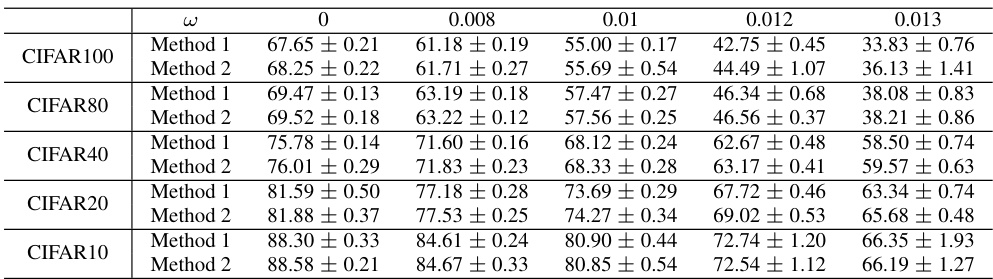
🔼 This table presents the performance comparison of different ECOCs (Error Correcting Output Codes) on two small-scale datasets: MNIST and CIFAR10. The performance is evaluated under varying levels of weight-errors (noise added to the weights), indicated by the ω values. Different ECOC methods are compared: one-hot, repetition, random, Hadamard, and the methods proposed in the paper (Method 1 for this table). The table shows that the proposed methods consistently outperform others, especially when significant weight errors are present.
read the caption
Table 1: Performance of different ECOCs with various code length (nL) on small scale tasks, i.e., MNIST and CIFAR10. The proposed method achieves better performance in the presence of weight-errors.
Full paper#