TL;DR#
Offline Reinforcement Learning (RL) faces challenges due to extrapolation error and overestimation, often attributed to over-generalization. Existing in-sample methods avoid this by only using training data, potentially sacrificing performance.
This paper introduces Doubly Mild Generalization (DMG), a novel approach that carefully exploits generalization. DMG comprises mild action generalization (selecting nearby actions) and mild generalization propagation (controlled bootstrapping), mitigating overestimation while benefiting from generalization. Extensive experiments demonstrate DMG’s state-of-the-art performance on various benchmarks, surpassing in-sample methods. Theoretical analysis further supports DMG’s effectiveness, guaranteeing better performance than in-sample methods under ideal conditions and providing a performance lower bound even in worst-case scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in offline reinforcement learning because it challenges the conventional wisdom of avoiding generalization entirely. By demonstrating that carefully controlled generalization can improve performance, it opens new avenues for algorithm development and pushes the field towards more robust and efficient offline RL methods. The theoretical analysis provides a strong foundation for future work, and the empirical results showcase the effectiveness of the proposed method on challenging benchmarks.
Visual Insights#

🔼 This figure shows the performance and Q-values of the Doubly Mild Generalization (DMG) algorithm as the mixture coefficient λ varies. The x-axis represents λ, ranging from 0 to 1. The y-axis shows both the normalized return (performance) and the Q-value. Multiple lines represent different locomotion tasks. The crosses indicate divergence of the value functions. The figure demonstrates that a moderate value of λ (mild generalization propagation) is crucial for optimal performance, while excessively high values of λ lead to divergence.
read the caption
Figure 1: Performance and Q values of DMG with varying mixture coefficient λ over 5 random seeds. The crosses × mean that the value functions diverge in several seeds. As λ increases, DMG enables stronger generalization propagation, resulting in higher and probably divergent learned Q values. Mild generalization propagation plays a crucial role in achieving strong performance.

🔼 This table compares different offline reinforcement learning (RL) methods based on two aspects of generalization: action generalization (whether the policy selects actions beyond the dataset) and generalization propagation (whether value training propagates generalization). It categorizes several offline RL algorithms as having none, mild, or full generalization in each aspect, highlighting the unique approach of the proposed Doubly Mild Generalization (DMG) method.
read the caption
Table 1: Comparison of offline RL work from the generalization perspective.
In-depth insights#
Offline RL Generalization#
Offline reinforcement learning (RL) presents unique challenges due to its reliance on fixed datasets, limiting the ability to explore and potentially leading to poor generalization. Extrapolation error arises when the agent encounters situations unseen during training, leading to inaccurate value estimations. Overestimation is another crucial issue stemming from the inherent uncertainty in estimating the value function. Addressing these limitations involves careful consideration of how the agent generalizes its knowledge. In-sample learning methods avoid extrapolation by restricting predictions to the training data. However, these approaches may forgo potential performance gains from reasonable generalization. Strategies such as careful regularization or data augmentation can enhance the generalization ability, but achieving a balance between generalization and overfitting remains a key challenge. Ultimately, effective offline RL generalization necessitates a thorough understanding of the data distribution and the agent’s capacity to learn and apply knowledge beyond the training distribution.
Doubly Mild Generalization#
The concept of “Doubly Mild Generalization” in offline reinforcement learning offers a nuanced approach to handling the inherent challenges of extrapolation error and value overestimation. It suggests that carefully controlled generalization, rather than complete avoidance, can improve performance. Mild action generalization focuses on selecting actions within a close neighborhood of the training data, maximizing Q-values while limiting the risk of venturing into unreliable out-of-distribution regions. Mild generalization propagation, the second aspect, directly addresses the compounding of errors through bootstrapping. By blending mildly generalized and in-sample maximums in the Bellman target, it moderates the spread of potential errors. This dual approach balances the benefits of generalization (improved performance) with the need to mitigate its risks (overestimation and extrapolation). The theoretical analysis strengthens this idea, suggesting better performance than in-sample methods under ideal generalization and performance bounds even in worst-case scenarios. This method’s flexibility allows a seamless transition from offline to online learning, showcasing its practical potential.
DMG Theoretical Analysis#
A thorough DMG theoretical analysis would involve examining its behavior under various generalization scenarios. Oracle generalization, assuming perfect generalization within a close neighborhood of the training data, would demonstrate DMG’s ability to surpass in-sample methods. Conversely, a worst-case generalization analysis, considering potential errors in generalization, would establish performance bounds and robustness. This involves proving that DMG’s value overestimation remains controlled even with poor generalization, ensuring a safe and performant policy. The theoretical analysis should also cover the convergence properties of the DMG operator, demonstrating that it reliably converges to a unique solution under specific conditions. Finally, comparisons against existing in-sample and traditional offline RL methods would highlight DMG’s theoretical advantages, potentially proving bounds on performance improvement in specific settings. The analysis should rigorously establish these claims through sound mathematical arguments and formal proofs.
DMG Algorithm#
The Doubly Mild Generalization (DMG) algorithm presents a novel approach to offline reinforcement learning by carefully balancing generalization and its potential pitfalls. DMG’s core innovation lies in its “doubly mild” strategy, encompassing mild action generalization, selecting actions near the dataset’s support to maximize Q-values, and mild generalization propagation, which mitigates the accumulation of errors during bootstrapping by blending generalized and in-sample updates. This approach avoids the over-generalization issues common in offline RL, allowing for improved performance. Theoretically, DMG offers performance guarantees, surpassing in-sample optimal policies under ideal conditions and maintaining performance bounds even under worst-case scenarios. Empirically, DMG achieves state-of-the-art results on various benchmark tasks, demonstrating its effectiveness and versatility. Its flexibility further allows for a seamless transition between offline and online learning, making it a strong contender for real-world applications.
Future Work#
Future research directions stemming from this doubly mild generalization (DMG) approach in offline reinforcement learning (RL) could involve several key areas. Extending DMG to handle more complex scenarios such as continuous action spaces and partial observability would significantly broaden its applicability. Investigating the impact of different function approximators beyond neural networks and exploring more sophisticated generalization propagation mechanisms beyond simple blending could lead to improved performance and robustness. A thorough empirical comparison across a wider range of offline RL benchmarks and a more in-depth theoretical analysis focusing on specific generalization bounds and value estimation guarantees are also critical. Finally, exploring the integration of DMG with other offline RL techniques like model-based methods and incorporating uncertainty estimation directly into the DMG framework would further enhance its capabilities and address potential limitations.
More visual insights#
More on figures

🔼 The figure displays the performance and Q-values of the Doubly Mild Generalization (DMG) algorithm with varying penalty coefficient (v). It shows that as the penalty coefficient decreases, the algorithm allows for broader action generalization, leading to higher Q-values. However, the optimal performance is achieved with a moderate level of action generalization, demonstrating the importance of balancing generalization for achieving optimal results. The results are averaged across five random seeds, enhancing the reliability of the observations. The plots highlight the relationship between the penalty coefficient, the resulting Q values, and the overall performance of the algorithm.
read the caption
Figure 2: Performance and Q values of DMG with varying penalty coefficient v over 5 random seeds. As v decreases, DMG allows broader action generalization, leading to larger learned Q values. Mild action generalization is also critical for attaining superior performance.
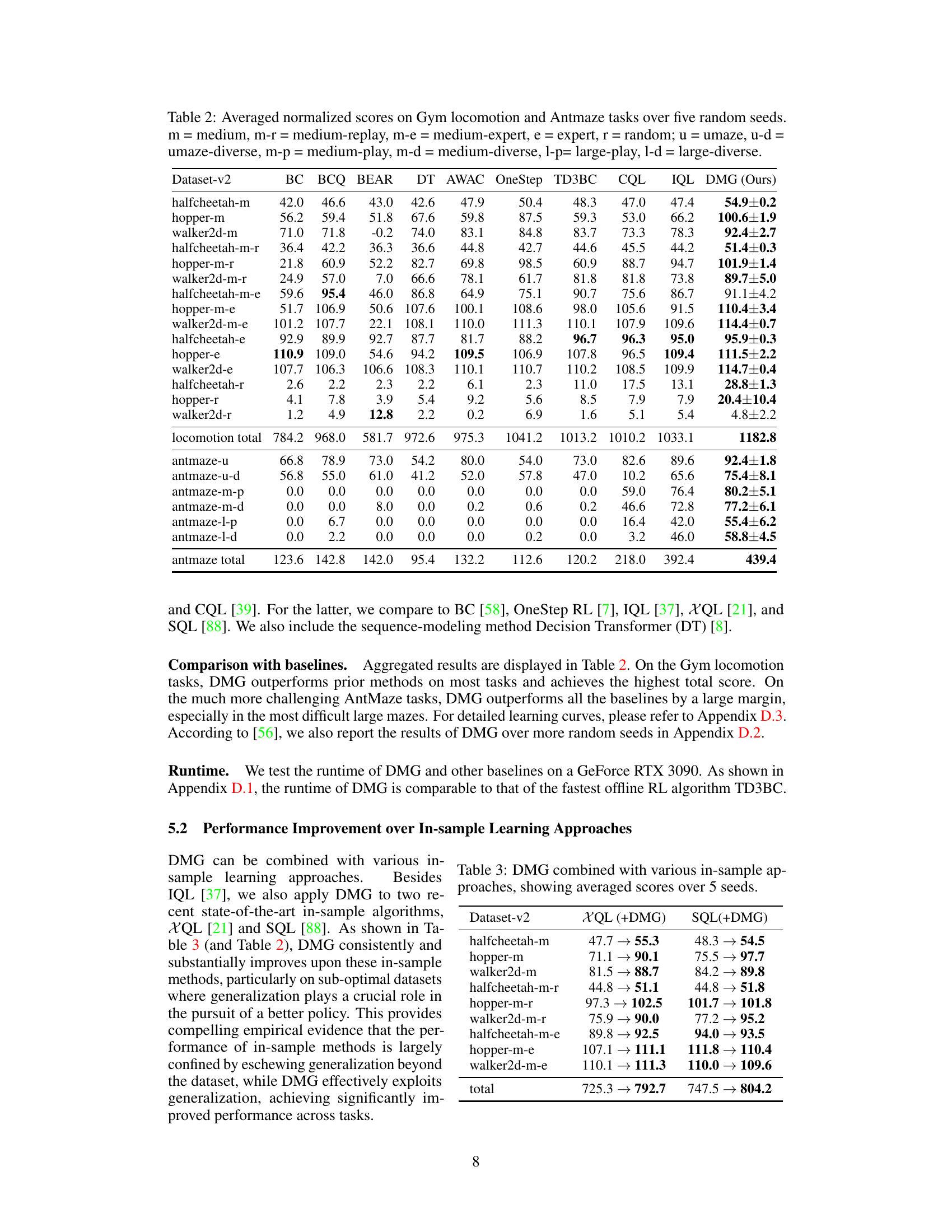
🔼 This figure shows the runtime of different offline reinforcement learning algorithms on a specific task, halfcheetah-medium-replay-v2, using a GeForce RTX 3090 GPU. The algorithms compared are Decision Transformer (DT), MOPO, CQL, AWAC, the proposed Doubly Mild Generalization (DMG), IQL, and TD3BC. The bar chart visually represents the runtime of each algorithm, with DMG showing a runtime comparable to TD3BC, one of the faster methods.
read the caption
Figure 3: Runtime of algorithms on halfcheetah-medium-replay-v2 on a GeForce RTX 3090.
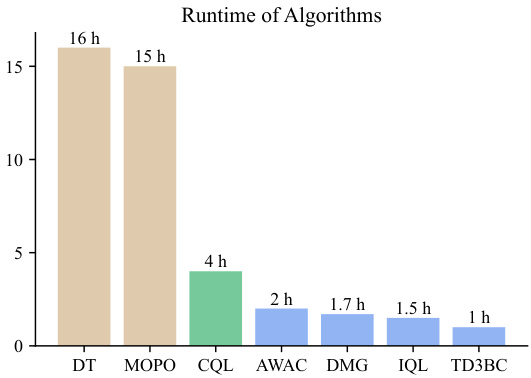
🔼 This figure displays the learning curves of the Doubly Mild Generalization (DMG) algorithm during offline training on various Gym locomotion tasks. The performance, measured as episode return, is plotted against the number of gradient steps. Each line represents the average performance over 5 different random seeds, with the shaded region indicating the standard deviation. This visualization allows for assessing the stability and convergence speed of the DMG algorithm across different random initializations for each task. The x-axis shows the number of gradient steps (in millions), and the y-axis shows the episode return.
read the caption
Figure 4: Learning curves of DMG on Gym locomotion tasks during offline training. The curves are averaged over 5 random seeds, with the shaded area representing the standard deviation across seeds.
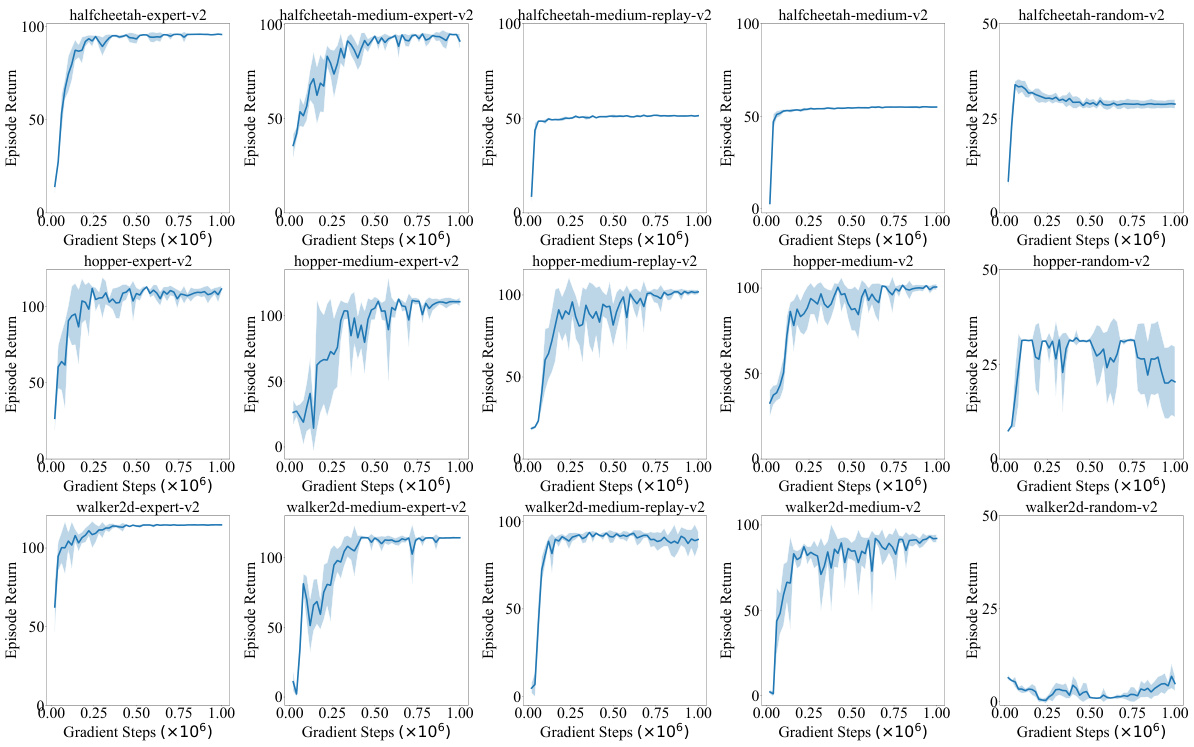
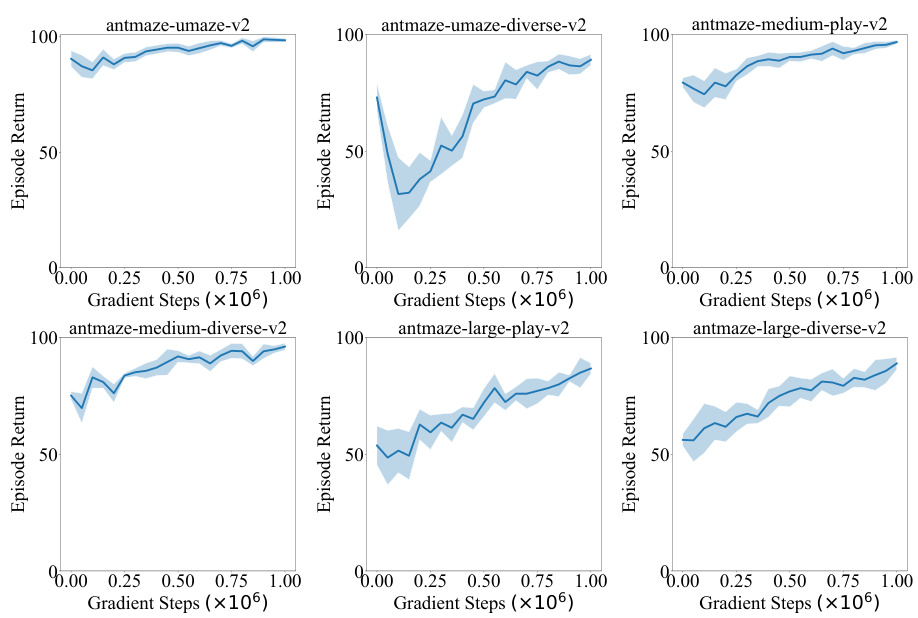
🔼 This figure shows the learning curves of the Doubly Mild Generalization (DMG) algorithm on six AntMaze tasks from the D4RL benchmark. Each curve represents the average episode return over five random seeds, and the shaded region shows the standard deviation. The x-axis represents the number of gradient steps during offline training, and the y-axis represents the average episode return. The figure demonstrates the performance of DMG on various AntMaze environments, revealing its learning progress and stability across different scenarios.
read the caption
Figure 5: Learning curves of DMG on Antmaze tasks during offline training. The curves are averaged over 5 random seeds, with the shaded area representing the standard deviation across seeds.
🔼 This figure shows the learning curves of the Doubly Mild Generalization (DMG) algorithm on six different AntMaze tasks during offline training. Each curve represents the average episode return over five random seeds, and the shaded region indicates the standard deviation. The x-axis represents the number of gradient steps (in millions), and the y-axis represents the average episode return. The figure illustrates the learning progress of DMG across various AntMaze environments with different levels of complexity and data distributions.
read the caption
Figure 5: Learning curves of DMG on Antmaze tasks during offline training. The curves are averaged over 5 random seeds, with the shaded area representing the standard deviation across seeds.
More on tables

🔼 This table summarizes various offline reinforcement learning (RL) methods from the perspective of generalization. It categorizes the methods based on two key aspects of generalization: Action Generalization (whether the policy training intentionally selects actions beyond the dataset to maximize Q-values) and Generalization Propagation (whether value training propagates generalization through bootstrapping). The table shows the different levels of generalization utilized by each method (none, mild, or full). It helps to illustrate the unique approach of Doubly Mild Generalization (DMG) in mitigating the issues of over-generalization often seen in offline RL.
read the caption
Table 1: Comparison of offline RL work from the generalization perspective.

🔼 This table presents the average normalized scores achieved by different offline reinforcement learning algorithms on various Gym locomotion and Antmaze tasks. The results are averaged over five different random seeds for each task. The table provides a comparison of the performance of DMG (Doubly Mild Generalization), the proposed method, against several baseline algorithms including BCQ, BEAR, AWAC, TD3BC, CQL, IQL, and others. Different dataset variations (e.g., medium, expert, random) are also included for comparison.
read the caption
Table 2: Averaged normalized scores on Gym locomotion and Antmaze tasks over five random seeds. m = medium, m-r = medium-replay, m-e = medium-expert, e = expert, r = random; u = umaze, u-d = umaze-diverse, m-p = medium-play, m-d = medium-diverse, l-p= large-play, l-d = large-diverse.
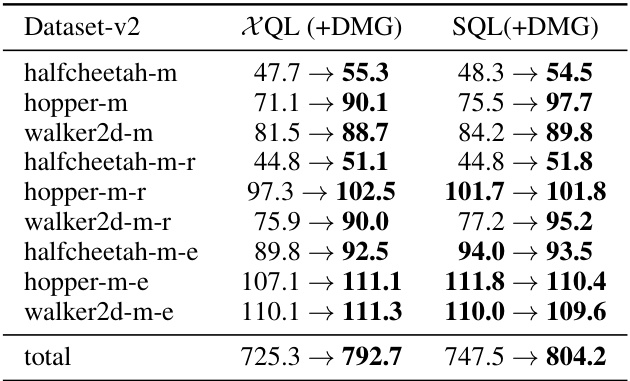
🔼 This table presents the results of combining the Doubly Mild Generalization (DMG) method with three different in-sample learning approaches (XQL, SQL, and IQL) on several benchmark tasks. It demonstrates the performance improvement achieved by incorporating DMG into existing in-sample methods, highlighting the benefits of mild generalization in offline reinforcement learning.
read the caption
Table 3: DMG combined with various in-sample approaches, showing averaged scores over 5 seeds.
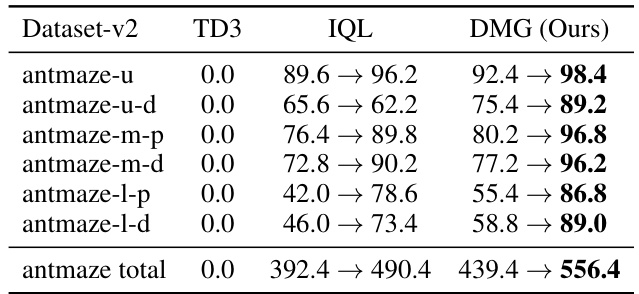
🔼 This table presents the results of online fine-tuning experiments on AntMaze tasks. It compares the performance of three algorithms: TD3 (trained from scratch), IQL, and DMG. The table shows the normalized scores achieved after offline training and then after an additional 1 million steps of online fine-tuning. The results highlight DMG’s superior online fine-tuning performance, demonstrating a seamless transition from offline to online learning.
read the caption
Table 4: Online fine-tuning results on AntMaze tasks, showing normalized scores of offline training and 1M steps online fine-tuning, averaged over 5 seeds.
🔼 The table compares several offline reinforcement learning methods based on two aspects: action generalization (whether the policy selects actions beyond the dataset) and generalization propagation (whether value training propagates generalization through bootstrapping). It categorizes existing methods into those with none, mild, or full generalization in each aspect, highlighting the unique position of the proposed DMG method.
read the caption
Table 1: Comparison of offline RL work from the generalization perspective.

🔼 This table compares the performance of the Doubly Mild Generalization (DMG) algorithm on D4RL offline training tasks using two different evaluation criteria. The first uses the mean and standard deviation (SD) calculated over five random seeds, while the second uses the mean and 95% confidence interval (CI) calculated over ten random seeds. This allows for a comparison of the algorithm’s robustness and consistency across different runs and evaluation methods.
read the caption
Table 6: Comparison of DMG under different evaluation criteria on D4RL offline training tasks.
Full paper#