TL;DR#
Traditional machine learning theory suggests that overfitting noisy training data leads to poor generalization. However, recent empirical studies show that some models, even when perfectly fitting noisy data, can still generalize well; this is known as ‘benign overfitting’. This paper focuses on Gaussian kernel ridgeless regression, a type of minimum-norm interpolating solution, to investigate this phenomenon by analyzing how the model’s performance changes as the size of the dataset and the input dimensionality vary.
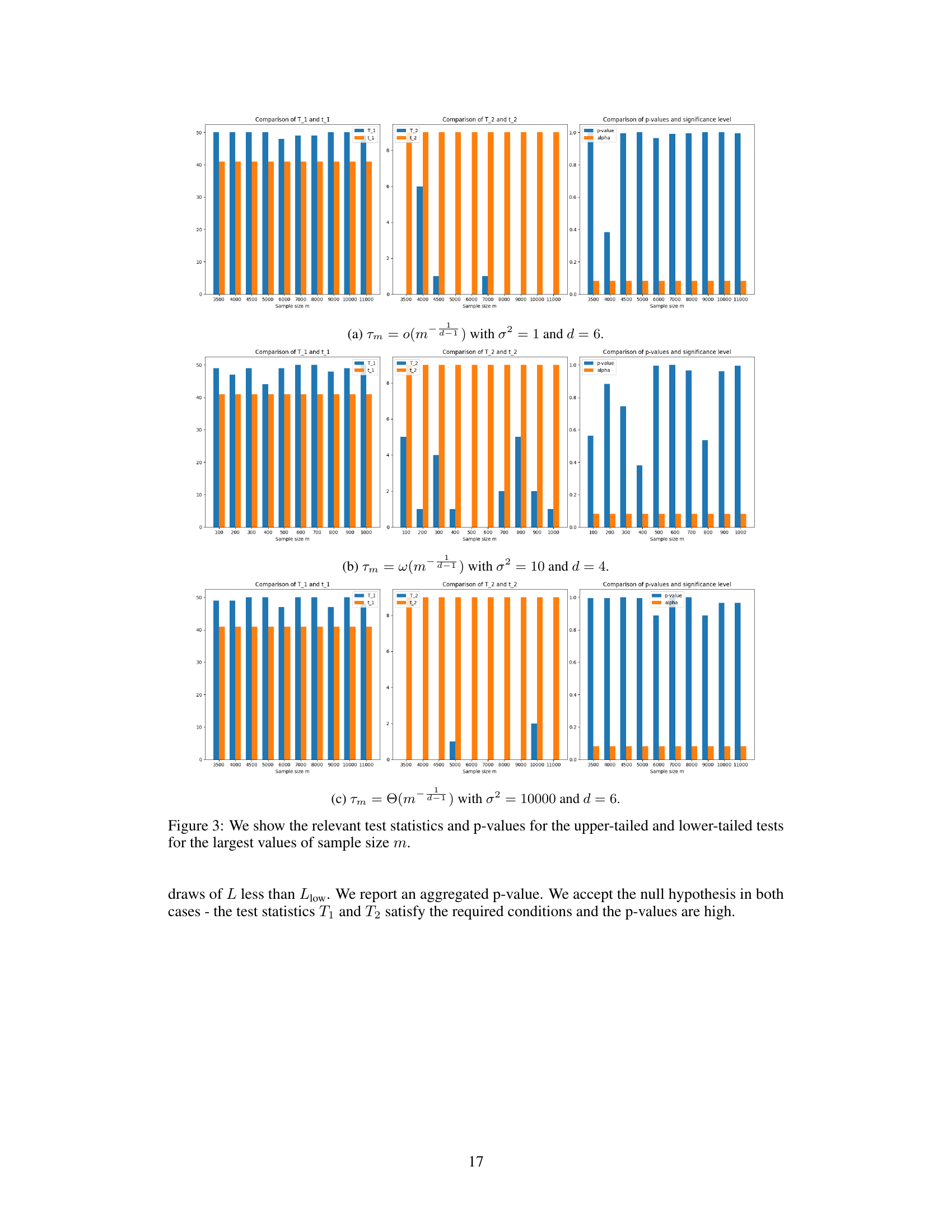
This study examines overfitting behavior by varying bandwidth or dimensionality. For fixed dimensions, the analysis shows inconsistent results and performance inferior to a null predictor. However, when increasing the dimensionality sub-polynomially with the sample size, the authors demonstrate an example of benign overfitting, providing a new understanding of the trade-off between model complexity and generalization ability. The research utilizes theoretical tools, notably risk predictions based on kernel eigenstructure, to analyze the behavior of the ridgeless solution in various scenarios, and this contributes to a more comprehensive understanding of overfitting in kernel methods.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges conventional wisdom in machine learning, demonstrating that interpolation, previously viewed as catastrophic, can lead to surprisingly good generalization under specific conditions. It provides a theoretical framework for understanding this phenomenon and opens new avenues for research in areas like benign overfitting and the impact of dimensionality on generalization.
Visual Insights#
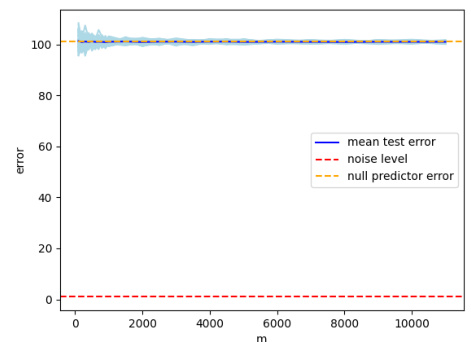
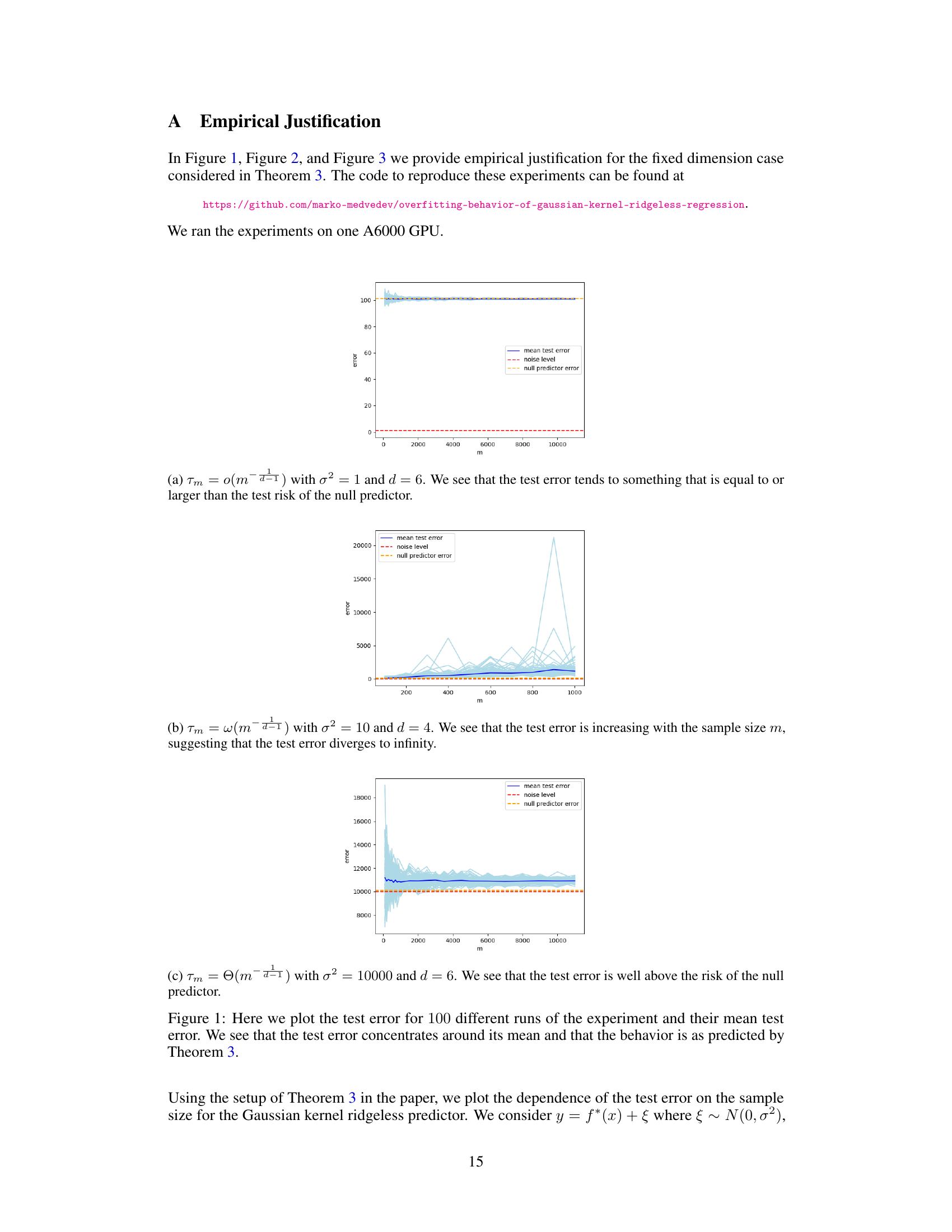
🔼 This figure shows the results of the experiment for the fixed dimension case considered in Theorem 3 of the paper. The plot displays the test error for 100 different runs of the experiment, along with their mean test error. The error bars represent the standard deviation of the test error across the different runs. The figure demonstrates that the test error concentrates around its mean, which supports the theoretical predictions of Theorem 3. Specifically, it shows that even with varying bandwidth, the minimum norm interpolating solution of Gaussian KRR is not consistent and is generally worse than the null predictor.
read the caption
Figure 1: Here we plot the test error for 100 different runs of the experiment and their mean test error. We see that the test error concentrates around its mean and that the behavior is as predicted by Theorem 3.
In-depth insights#
Gaussian Overfitting#
Gaussian overfitting, a phenomenon where Gaussian kernel ridge regression models exhibit unexpectedly high test error despite perfectly fitting noisy training data, is a complex issue. The paper explores this phenomenon by varying bandwidth and dimensionality, revealing crucial insights into the interplay between these factors and the model’s generalization capabilities. For fixed dimensionality, regardless of bandwidth selection, the model consistently fails to generalize, often performing worse than a null predictor. This highlights that even well-tuned bandwidths do not guarantee consistency. In contrast, when dimensionality scales with sample size, a more nuanced behavior emerges. The study reveals that sub-polynomial scaling of dimensionality can lead to benign overfitting, showcasing a unique scenario where the test error converges to the Bayes optimal risk. This result is particularly significant as it challenges the traditional view of overfitting, which assumes poor generalization with increasing model complexity. The use of Gaussian universality ansatz and risk predictions based on kernel eigenstructure are crucial components of the analysis, yet understanding their limitations and applicability to diverse scenarios remains an important area of future research.
Varying Bandwidths#
The concept of varying bandwidths in the context of Gaussian kernel ridgeless regression is crucial for understanding the model’s overfitting behavior. Bandwidth directly influences the kernel’s receptive field, impacting how the model weighs nearby data points during training. A small bandwidth leads to high variance and localized fits, easily overfitting noisy data. Conversely, a large bandwidth results in a smoother model that might underfit. The research likely investigates how adjusting bandwidth as the sample size grows influences generalization. Optimal bandwidth selection is critical: tuning the bandwidth is common in practice but may not prevent overfitting completely. The study likely explores if adapting bandwidth according to some scaling relationship with the sample size can mitigate overfitting. Theoretical analysis is important to understand asymptotic behavior and determine if varying bandwidth leads to consistency (i.e., the model converges to the true function as data increases). The paper likely considers different scaling scenarios and investigates whether any scaling strategy avoids the catastrophic overfitting observed with fixed bandwidths, possibly finding a sweet spot between underfitting and overfitting.
Dimension Scaling#
The study investigates the impact of varying dimensionality alongside sample size on the overfitting behavior of Gaussian kernel ridgeless regression. A key focus is on how the dimensionality scales relative to the sample size, moving beyond prior polynomial scaling analyses to explore sub-polynomial scalings. The researchers derive both upper and lower bounds on the test risk for arbitrary dimension scaling, demonstrating the conditions under which benign, tempered, or catastrophic overfitting occur. Specifically, the analysis reveals a crucial interplay between eigenvalue decay, multiplicity of eigenvalues and dimensionality scaling, determining the nature of overfitting. An important finding is the identification of sub-polynomial dimension scalings that exhibit benign overfitting, a novel contribution that extends our understanding of generalization behavior in high-dimensional settings. Finally, the results highlight the importance of carefully considering dimensionality scaling when applying kernel methods, as the choice of scaling significantly impacts generalization performance.
Eigenframework Risk#
The Eigenframework Risk is a crucial concept for understanding the generalization performance of kernel methods. It leverages the eigenspectrum of the kernel, which provides a powerful tool for analyzing the risk in high-dimensional settings. The Eigenframework’s key contribution lies in its ability to predict the test risk using a closed-form expression. This formula depends on the eigenvalues of the kernel, the noise level, and regularization parameters. It offers a valuable tool for analyzing the behavior of Kernel Ridge Regression (KRR), even in regimes where traditional methods struggle. The Gaussian universality ansatz and non-rigorous risk predictions are significant assumptions underlining its application. This allows us to study various scenarios such as varying bandwidths and increasing dimensionality. For fixed dimensions, the Eigenframework shows that ridgeless solutions are not consistent, often performing poorly. With increasing dimensionality, it reveals the relationship between dimensionality scaling and the nature of overfitting (benign, tempered, catastrophic). The approach’s power to uncover the link between eigenstructure, dimensionality, and overfitting is extremely valuable. Understanding this Eigenframework Risk prediction is critical for improving generalization and avoiding catastrophic overfitting in kernel methods.
Future Directions#
Future research could explore extending the analysis beyond the Gaussian kernel to other kernel types, investigating how kernel choice affects overfitting behavior and the applicability of the theoretical findings. A crucial next step is rigorous mathematical validation of the eigenframework’s predictions, as current work relies on non-rigorous risk predictions that are empirically well-supported. The impact of different noise distributions beyond the Gaussian assumption warrants further exploration. Investigating how the results generalize to non-uniform input data distributions would significantly broaden the work’s applicability to real-world scenarios. Finally, developing more precise and theoretically grounded risk predictions for a wider range of kernel-dimensionality-sample size relationships remains a key challenge for future research.
More visual insights#
More on figures
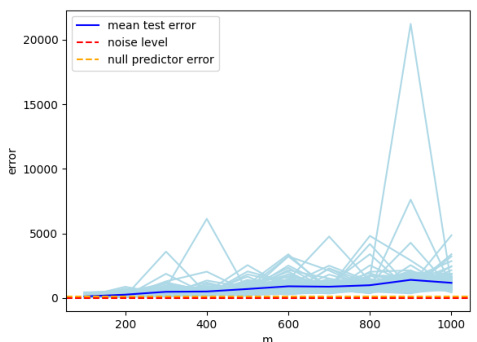
🔼 This figure empirically validates Theorem 3 of the paper by visualizing the test error for 100 runs of the experiment, along with the mean test error. The plot shows that the test error distribution is concentrated around its mean, thus supporting the predictions made by Theorem 3 regarding the overfitting behavior of Gaussian kernel in fixed dimension. The different colored lines represent individual runs while the blue line shows the average test error.
read the caption
Figure 1: Here we plot the test error for 100 different runs of the experiment and their mean test error. We see that the test error concentrates around its mean and that the behavior is as predicted by Theorem 3.
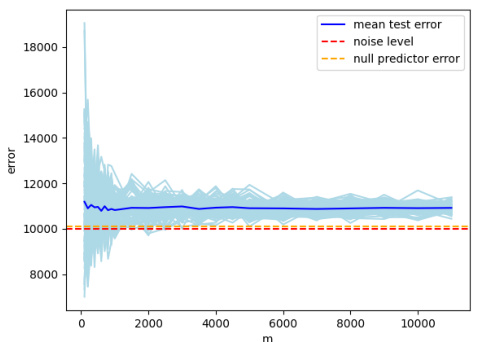
🔼 This figure shows the test error for 100 independent runs of an experiment, along with the mean test error. The plot visually demonstrates that the observed test error tightly clusters around the mean, thus supporting the theoretical predictions of Theorem 3 regarding the overfitting behavior of Gaussian kernel ridge regression with varying bandwidth.
read the caption
Figure 1: Here we plot the test error for 100 different runs of the experiment and their mean test error. We see that the test error concentrates around its mean and that the behavior is as predicted by Theorem 3.

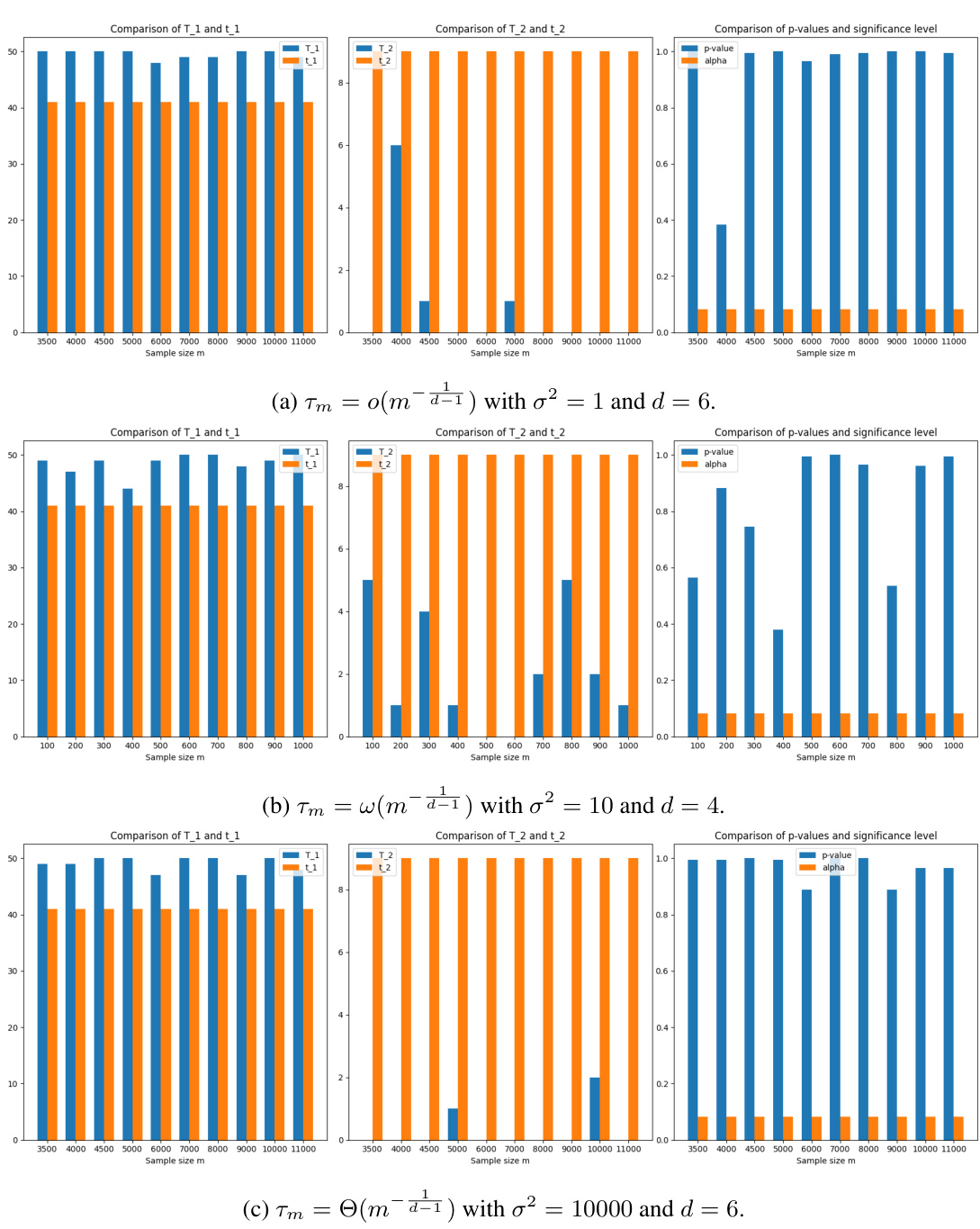
🔼 This figure shows the empirical justification for the fixed dimension case considered in Theorem 3 of the paper. It presents the test error for 100 different runs of the experiment, along with the mean test error. The plot visually demonstrates that the test error distribution is concentrated around its mean, thus aligning with the predictions made by Theorem 3. Three subplots are shown corresponding to three different bandwidth scaling scenarios; each subplot provides strong visual evidence that supports the findings of the theorem regarding the overfitting behavior of the Gaussian kernel in a fixed dimension.
read the caption
Figure 1: Here we plot the test error for 100 different runs of the experiment and their mean test error. We see that the test error concentrates around its mean and that the behavior is as predicted by Theorem 3.
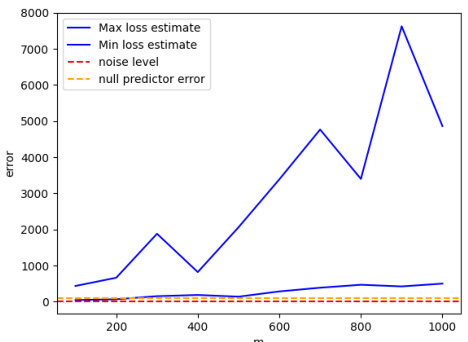
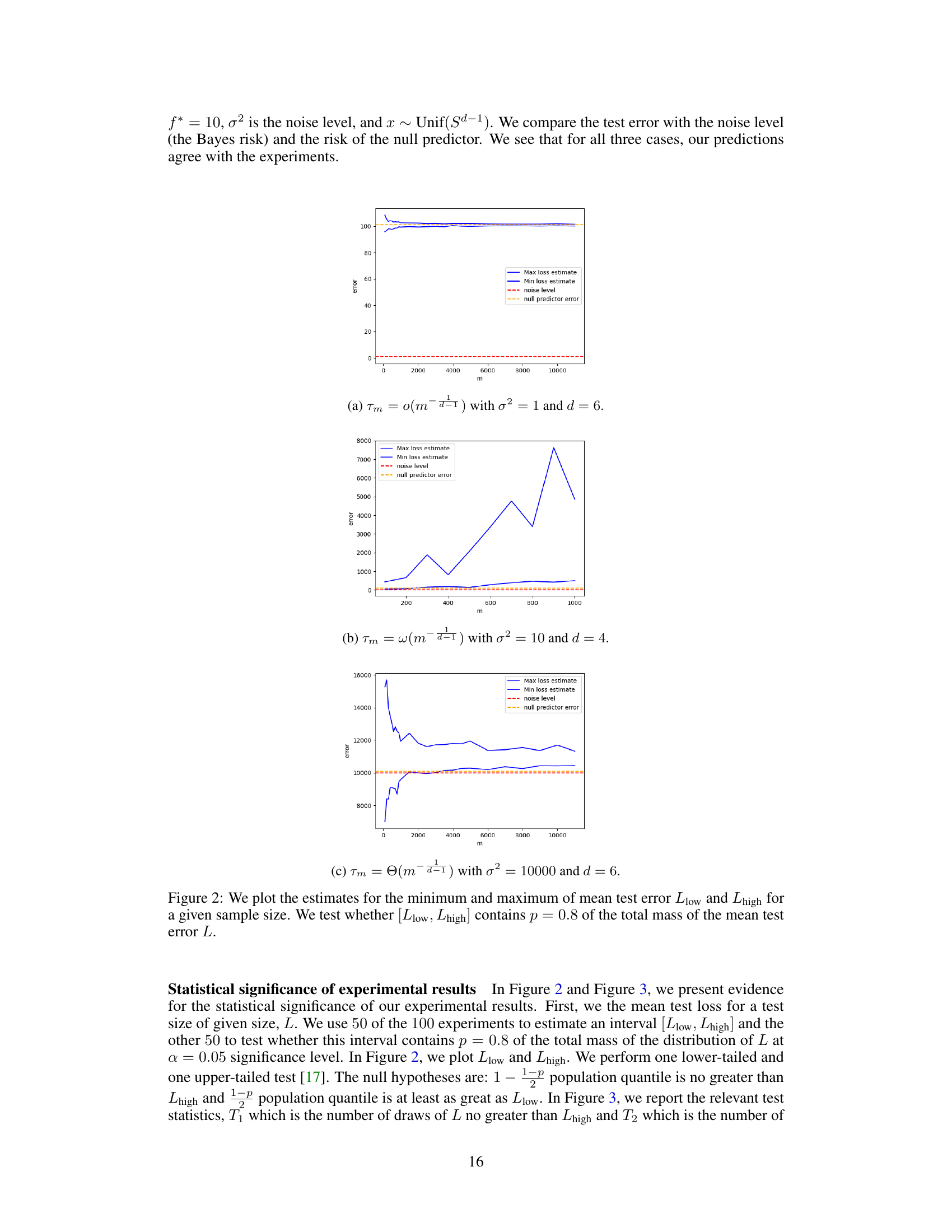
🔼 This figure shows the mean test error for three different settings of bandwidth. In each setting, a minimum and maximum error value are shown with an interval designed to contain 80% of the error’s mass. This provides empirical support for the theoretical predictions of Theorem 3.
read the caption
Figure 2. We plot the estimates for the minimum and maximum of mean test error, Llow and Lhigh, for a given sample size. We test whether [Llow, Lhigh] contains p = 0.8 of the total mass of the mean test error, L, for a given sample size.

🔼 This figure shows the results of 100 different experimental runs for three different bandwidth scaling regimes. The blue lines represent the maximum and minimum test error, while the red line shows the noise level (Bayes risk), and the yellow line represents the null predictor’s error. The figure empirically validates Theorem 3 by showing that the test error concentrates around its mean, with the behavior in line with the theoretical predictions of the theorem.
read the caption
Figure 1: Here we plot the test error for 100 different runs of the experiment and their mean test error. We see that the test error concentrates around its mean and that the behavior is as predicted by Theorem 3.
🔼 This figure shows the results of three experiments on Gaussian kernel ridgeless regression with varying bandwidth parameters. Subfigure (a) shows a scenario where the bandwidth scaling is o(m^−d/1), resulting in a test error that approaches a constant value greater than the null predictor’s risk. Subfigure (b) illustrates a case with bandwidth scaling w(m^−d/1), leading to a test error that increases with the sample size, indicating catastrophic overfitting. Finally, subfigure (c) depicts a situation with O(m^−d/1) bandwidth scaling, where the test error remains above the null predictor’s risk despite reaching a constant value eventually. The experiment results support the findings of Theorem 3.
read the caption
Figure 1: Here we plot the test error for 100 different runs of the experiment and their mean test error. We see that the test error concentrates around its mean and that the behavior is as predicted by Theorem 3.
Full paper#