TL;DR#
Reinforcement learning (RL) often relies on linear transition models, limiting applicability to complex real-world scenarios. The multinomial logistic (MNL) model offers a more flexible, non-linear alternative, but existing RL algorithms for MNL models are computationally expensive or lack rigorous theoretical guarantees. This paper addresses these issues by presenting two novel randomized exploration algorithms, RRL-MNL and ORRL-MNL, which leverage the structure of the MNL model for efficient exploration and parameter estimation. These algorithms achieve statistically efficient regret bounds with constant-time computational cost per episode. The paper rigorously analyzes the regret guarantees for both algorithms and experimentally evaluates their performance on tabular MDPs and a variant of the RiverSwim problem, demonstrating superior performance compared to state-of-the-art MNL-MDP algorithms.
The paper focuses on addressing the challenges of RL with non-linear MNL transition models by proposing efficient algorithms that combine randomized exploration with online parameter estimation. RRL-MNL uses optimistic sampling for exploration and achieves a regret bound scaling with the problem-dependent constant κ−1, while the more advanced ORRL-MNL employs local gradient information to achieve a regret bound that has reduced dependence on к. This improved dependence on к is a significant contribution, as previous methods suffered from potentially large regret bounds due to a poor dependence on this constant. The authors also demonstrate the computational efficiency of their algorithms in comparison to existing MNL-MDP approaches.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in reinforcement learning (RL) and contextual bandits due to its novel algorithms for solving RL problems using multinomial logistic (MNL) function approximation, a significant departure from the limitations of linear models. It offers the first provably efficient randomized algorithms for MNL-MDPs, improving upon existing methods and opening new avenues for research in non-linear function approximation and computationally tractable methods. Its theoretical findings and experimental results provide valuable insights and benchmarks for future work in RL.
Visual Insights#
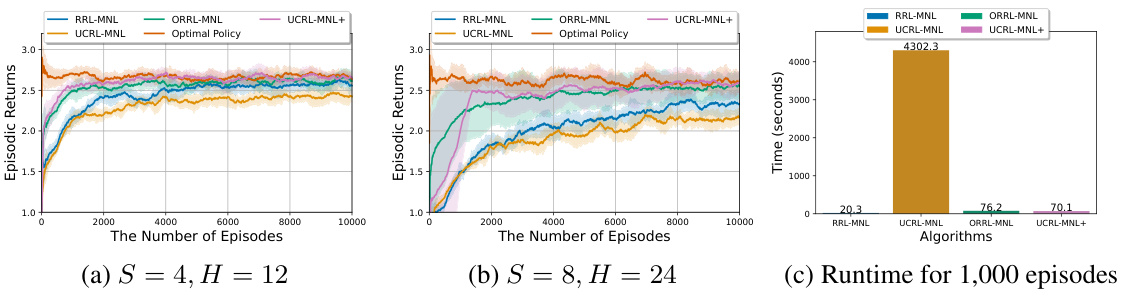
🔼 The figure shows the experimental results of the proposed algorithms (RRL-MNL, ORRL-MNL, UCRL-MNL+) and the existing state-of-the-art algorithm (UCRL-MNL) on a variant of the RiverSwim environment. Subfigure (a) and (b) display the episodic returns for different state and horizon sizes. Subfigure (c) compares the runtime of the algorithms for 1000 episodes. The results demonstrate that the proposed algorithms outperform UCRL-MNL in terms of both episodic return and computational efficiency. ORRL-MNL and UCRL-MNL+ converge faster to optimal performance than RRL-MNL and UCRL-MNL.
read the caption
Figure 1: Riverswim experiment results

🔼 This table compares different reinforcement learning algorithms in terms of their model-based approach, transition model used, reward setting, computational cost per episode, and regret bound. It highlights the differences and improvements of the proposed algorithms (RRL-MNL, ORRL-MNL, UCRL-MNL+) compared to existing methods. The table shows that the proposed algorithms achieve constant-time computational cost while maintaining favorable regret bounds.
read the caption
Table 1: This table compares the problem settings, online update, performance of the this paper with those of other methods in provable RL with function approximation. For computation cost, we only keep the dependence on the number of episode K.
Full paper#



















