TL;DR#
Many machine learning tasks involve optimizing an objective function that depends on some parameters. Estimating the gradient of the solution with respect to these parameters is critical for hyperparameter tuning, meta-learning and other tasks. A common approach is to differentiate through the iterations of the Stochastic Gradient Descent (SGD) algorithm, which is conceptually simple but requires careful analysis due to noise from SGD’s stochastic nature. Prior work has often focused on asymptotic convergence guarantees.
This research delves into the dynamics of SGD derivative estimates, showing that the convergence of the derivative iterates can be analyzed as a perturbed SGD recursion. The authors provide strong convergence results for strongly convex objective functions, determining convergence rates based on step-size schedules. This work presents rates of convergence for derivative estimates of SGD, particularly addressing constant step sizes and the practically relevant case of diminishing step sizes. The mathematical framework developed for the analysis provides further insights into inexact SGD recursions, potentially impacting the convergence analysis of other machine learning algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in stochastic optimization and machine learning. It provides a novel theoretical analysis of the dynamics of derivative estimation using SGD in parametric optimization, offering valuable insights into hyperparameter optimization and meta-learning. The findings open avenues for improved algorithm design and more robust convergence guarantees, impacting various applications of iterative differentiation in ML.
Visual Insights#
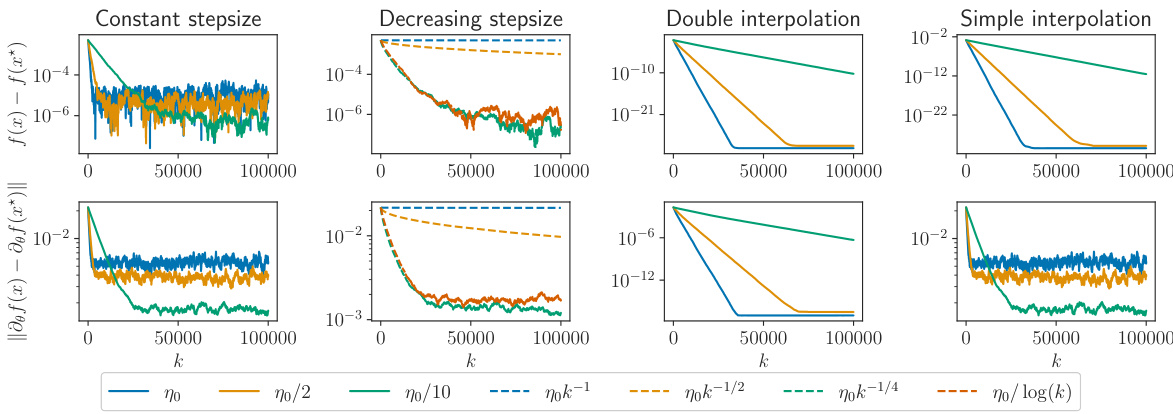
🔼 The figure shows the convergence behavior of SGD iterates and their Jacobian derivatives for ordinary least squares linear regression under different scenarios: constant step size, decreasing step size, double interpolation (σ=0 for both iterates and derivatives), and simple interpolation (σ=0 for iterates but not derivatives). Each column represents a different step-size strategy, visualizing the convergence of both the suboptimality (f(xk(θ))−f(x∗(θ))) and the derivative error (||∂θxk(θ)−∂θx∗(θ)||F). The results validate the theoretical convergence rates established in Theorem 2.2.
read the caption
Figure 1: Numerical behavior of SGD iterates and their derivatives (Jacobians) in a linear regression problem solved by ordinary least squares. The plots depict the convergence of the suboptimality f(xk(θ))−f(x∗(θ)) and the Frobenius norm of the derivative error ||∂θxk(θ)−∂θx∗(θ)||F across different experimental settings: constant step-size (first column), decreasing step-size (second column), double interpolation (third column), and simple interpolation (fourth column). The experiments utilize varying step-size strategies to illustrate general estimates, sublinear rates, and the impacts of interpolation regimes, validating theoretical predictions of Theorem 2.2.

🔼 This table summarizes the results from four different lemmas (C.1 to C.4) used in the convergence analysis of inexact SGD. Each lemma provides convergence results under different assumptions about step sizes, error terms, noise levels, and resulting convergence rates for the sequence (Dk)k∈N which represents the root of the mean squared error of the iterates. Lemma C.1 gives a result for constant step sizes, Lemmas C.2 and C.3 provides sublinear rates with vanishing step sizes, and Lemma C.4 shows an exponential convergence rate in the interpolation regime. The table helps to organize and understand the different convergence scenarios explored in the paper.
read the caption
Technical Lemmas
In-depth insights#
SGD Derivative Dynamics#
Analyzing the dynamics of Stochastic Gradient Descent (SGD) derivatives in the context of parametric optimization reveals crucial insights into the behavior of SGD iterates and their sensitivity to parameter changes. The core idea revolves around interpreting the derivative recursion of SGD iterates with respect to parameters as a perturbed SGD process itself. This perspective is powerful because it allows for leveraging existing convergence results of inexact SGD to understand the asymptotic behavior of the derivatives. Strong convexity of the objective function plays a critical role, ensuring the uniqueness and differentiability of the solution mapping, which is essential for analyzing the convergence of derivatives to the derivative of this mapping. The analysis reveals different convergence rates depending on the step-size scheduling: constant step-sizes lead to convergence within a noise ball, while diminishing step-sizes guarantee convergence to the true derivative. The theoretical findings are further supported by numerical experiments that demonstrate the practical implications of the developed theory in various settings.
Inexact SGD Recursion#
The concept of “Inexact SGD Recursion” centers on analyzing the behavior of Stochastic Gradient Descent (SGD) when the gradient calculations are imperfect. This inexactness stems from various sources, such as noisy estimations of the gradient from stochastic samples or computational errors in its calculation. The core idea revolves around treating the errors as an additional noise term in the standard SGD update rule. The analysis then shifts to investigating the convergence properties of this perturbed SGD recursion. Crucially, this approach allows for the study of the algorithm’s robustness to the inevitable inaccuracies present in many real-world applications, rather than relying on idealized, noise-free scenarios. A key finding might be establishing convergence bounds that depend on the magnitude of the errors, providing valuable insight into how this imperfection affects the ultimate solution quality and its convergence rate. The study of inexact SGD recursion is thus vital for understanding the practical performance of SGD in noisy environments and offers a pathway toward developing more robust and efficient optimization methods.
Convergence Rate Analysis#
A convergence rate analysis for an optimization algorithm rigorously examines how quickly the algorithm’s iterates approach the optimal solution. For stochastic gradient descent (SGD), this analysis is crucial because the inherent randomness introduces noise and complicates convergence behavior. A strong emphasis is often placed on demonstrating convergence rates in terms of the expected error (or its square) as a function of the number of iterations. The analysis often considers different scenarios such as using constant step sizes or diminishing step sizes. Constant step sizes can lead to convergence within a noise ball around the optimum, while diminishing step sizes often guarantee convergence to the exact solution, although possibly at a slower rate. The analysis also frequently considers the impact of algorithm parameters, such as the step size schedule and the strong convexity of the objective function. Strong convexity is vital as it ensures a unique optimum and helps obtain better convergence rates. The choice of step-size schedule significantly affects the convergence rate. For example, while a simple 1/k decay might provide a sub-linear rate, more sophisticated methods may achieve faster convergence. Ultimately, a rigorous convergence rate analysis provides essential guarantees about the algorithm’s performance and informs the selection of optimal parameters.
Hyperparameter Tuning#
Hyperparameter tuning is a critical aspect of machine learning model development, impacting model performance significantly. Effective tuning strategies are essential to optimize a model’s ability to generalize to unseen data. The process often involves exploring a vast search space of hyperparameter combinations, making it computationally expensive. Automated approaches, such as Bayesian optimization or evolutionary algorithms, offer efficient ways to navigate this space and find optimal configurations. However, the selection of a suitable tuning method depends on factors like the model’s complexity, the size of the dataset, and the computational resources available. Understanding the trade-offs between exploration and exploitation is crucial in hyperparameter tuning. Insufficient exploration may lead to suboptimal solutions, while excessive exploration can be computationally wasteful. Validation strategies, such as cross-validation or hold-out sets, are critical for evaluating the performance of different hyperparameter settings and preventing overfitting. The ultimate goal is to achieve a balance between model complexity and generalization capability to produce robust and reliable predictions. Advanced techniques like early stopping and regularization can further enhance the effectiveness of hyperparameter tuning by preventing overfitting and promoting better generalization.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the theoretical analysis to non-strongly convex or nonsmooth settings is crucial, as many real-world optimization problems fall outside this category. Investigating the impact of different step-size schedules and mini-batching strategies on the convergence of derivative estimates would provide valuable practical insights. A direct comparison between stochastic iterative differentiation and stochastic implicit differentiation would also be insightful, possibly revealing the relative strengths and weaknesses of each approach. Furthermore, developing efficient algorithms for computing hypergradients in high-dimensional spaces remains an open challenge, and exploring variance reduction techniques could lead to significant computational savings.
More visual insights#
More on figures

🔼 This figure shows the convergence of SGD iterates and their derivatives (Jacobians) in four different settings of linear regression problems solved by ordinary least squares. Each setting varies the step-size strategy used: constant, decreasing, double interpolation, and simple interpolation. The plots show the suboptimality (f(xk(θ))−f(x∗(θ))) and the Frobenius norm of the derivative error (||∂θxk(θ)−∂θx∗(θ)||F). The results validate the theoretical predictions of Theorem 2.2 from the paper. Each column represents a specific step size strategy and is accompanied by a corresponding subplot illustrating the convergence behavior of the derivatives.
read the caption
Figure 1: Numerical behavior of SGD iterates and their derivatives (Jacobians) in a linear regression problem solved by ordinary least squares. The plots depict the convergence of the suboptimality f(xk(θ))−f(x∗(θ)) and the Frobenius norm of the derivative error ||∂θxk(θ)−∂θx∗(θ)||F across different experimental settings: constant step-size (first column), decreasing step-size (second column), double interpolation (third column), and simple interpolation (fourth column). The experiments utilize varying step-size strategies to illustrate general estimates, sublinear rates, and the impacts of interpolation regimes, validating theoretical predictions of Theorem 2.2.

🔼 The figure displays the convergence behavior of SGD iterates and their Jacobian derivatives in four different experimental settings of linear regression using ordinary least squares. The settings vary the step size strategy (constant, decreasing) and the level of interpolation (simple, double). Each subplot shows the convergence of both the suboptimality (f(xk(θ)) - f(x*(θ))) and the Frobenius norm of the derivative error (||∂θxk(θ) - ∂θx*(θ)||F). The results illustrate the theoretical convergence rates and behaviors established in Theorem 2.2.
read the caption
Figure 1: Numerical behavior of SGD iterates and their derivatives (Jacobians) in a linear regression problem solved by ordinary least squares. The plots depict the convergence of the suboptimality f(xk(0)) − f(x*(0)) and the Frobenius norm of the derivative error ||дөхк (0) – дөх*(0) || F across different experimental settings: constant step-size (first column), decreasing step-size (second column), double interpolation (third column), and simple interpolation (fourth column). The experiments utilize varying step-size strategies to illustrate general estimates, sublinear rates, and the impacts of interpolation regimes, validating theoretical predictions of Theorem 2.2.
Full paper#



















