TL;DR#
Optimal transport (OT) is a powerful tool for aligning datasets, but existing entropic OT (EOT) solvers are difficult to tune due to hyperparameters impacting performance. The hyperparameter, ε, controls the regularization strength and influences computation speed, statistical performance, and generalization. Incorrect settings lead to biased results. This paper tackles the challenge of effectively using EOT.
The authors introduce PROGOT, a new class of EOT solvers that overcome these issues. PROGOT leverages dynamic OT formulations to optimize EOT computation by dividing mass displacement using time discretization and scheduling parameters. PROGOT estimates both OT plans and maps, demonstrating superior speed and robustness compared to traditional EOT and neural network approaches. The method’s statistical consistency is also theoretically established.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with optimal transport, particularly those dealing with large-scale datasets. PROGOT offers a faster, more robust alternative to existing methods, addressing the challenge of hyperparameter tuning in entropic optimal transport. Its proven statistical consistency and ability to handle large datasets opens new avenues for applications in machine learning and other fields.
Visual Insights#
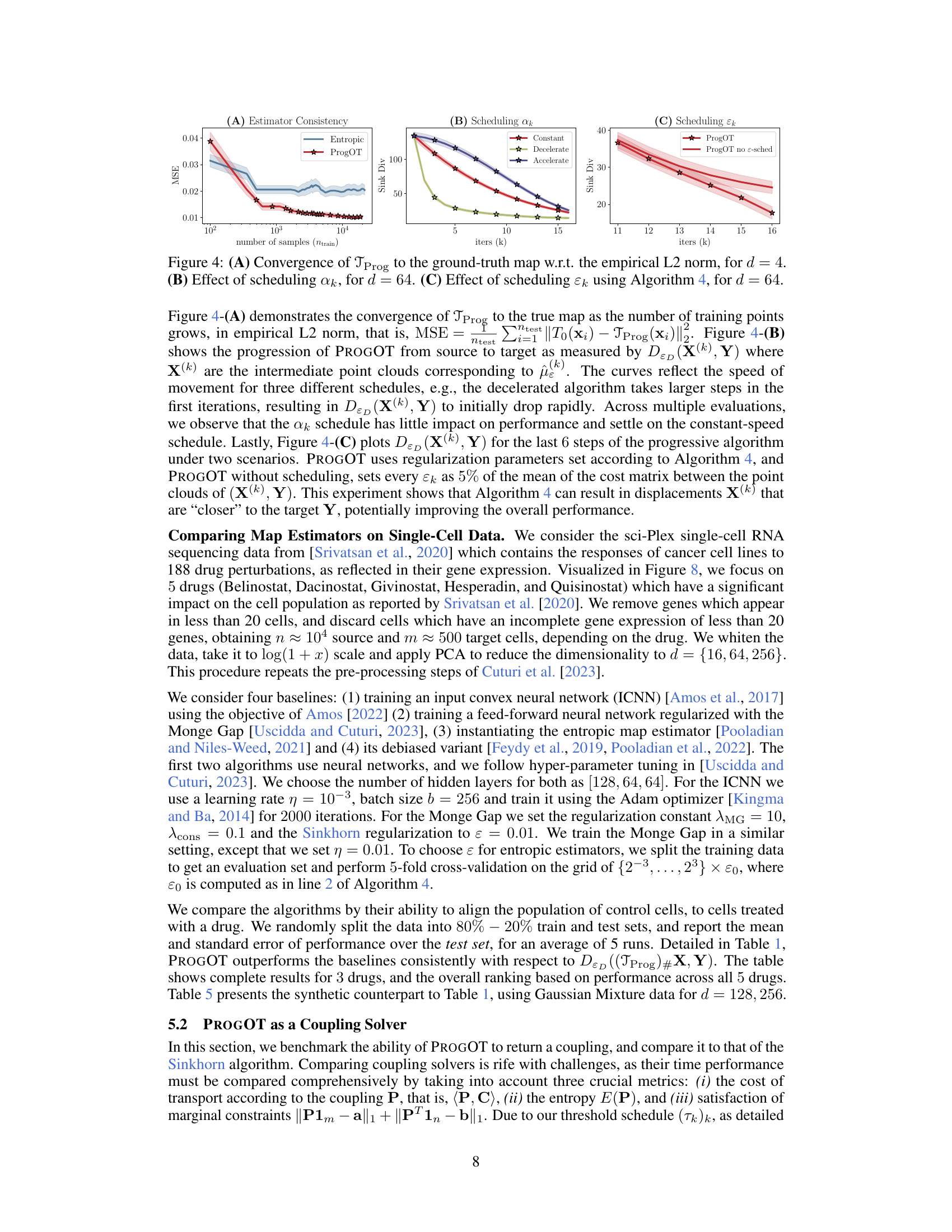
🔼 This figure shows a comparison of three different optimal transport (OT) solvers: EOT, Debiased EOT, and PROGOT. The figure illustrates how the choice of the regularization parameter ε affects the performance of EOT solvers, leading to biased map estimators and blurry couplings. It also highlights how PROGOT, which uses a progressive scheduling scheme, addresses these issues by producing a coupling with tunable entropy and a fast and reliable map estimator.
read the caption
Figure 1: (left) EOT solvers collapse when the value of ε is not properly chosen. This typically results in biased map estimators and in blurry couplings (see Fig. 2 for the coupling matrix obtained between Xtrain and ytrain). (middle) Debiasing the output of EOT solvers can prevent a collapse to the mean seen in EOT estimators, but computes the same coupling. PROGOT (right) ameliorates these problems in various ways: by decomposing the resolution of the OT problem into multiple time steps, and using various forms of progressive scheduling, we recover both a coupling whose entropy can be tuned automatically and a map estimator that is fast and reliable.
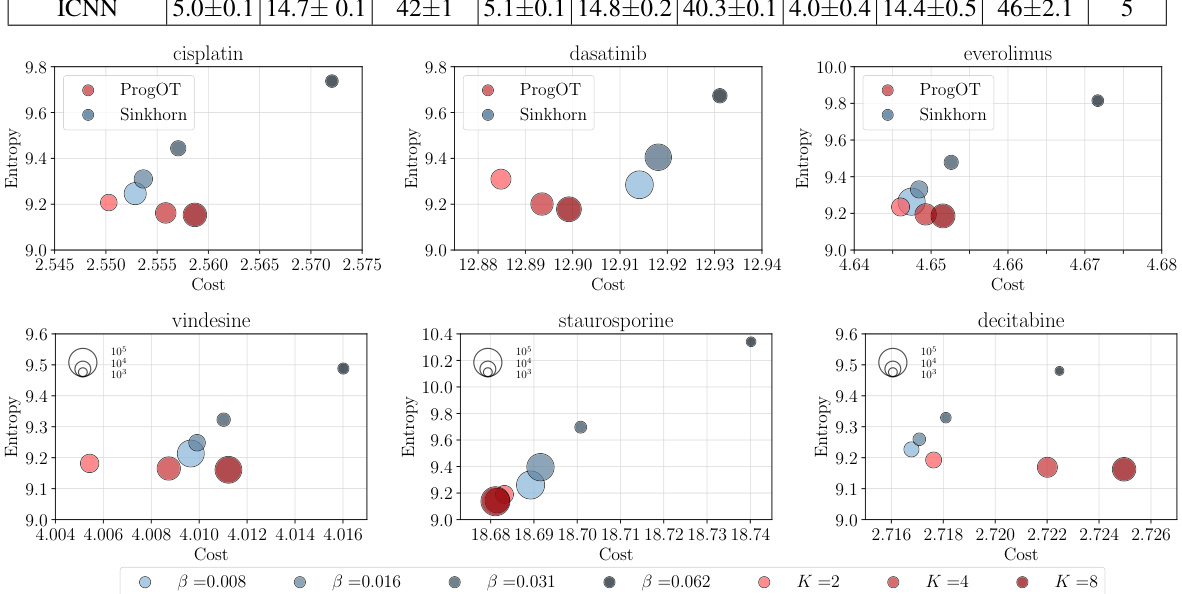
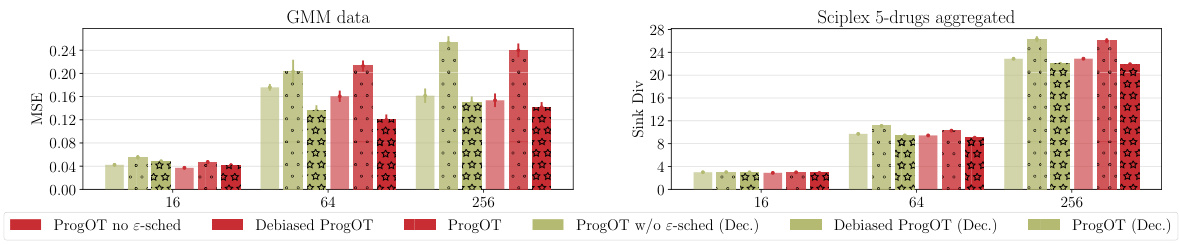
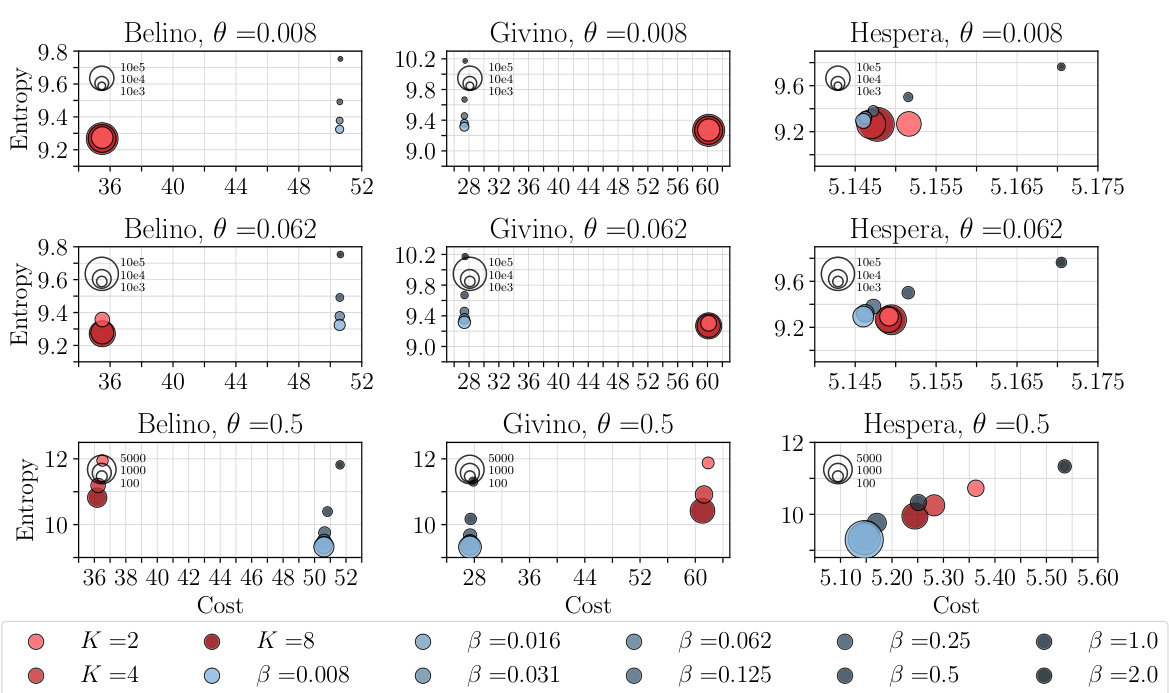
🔼 This table compares the performance of the proposed PROGOT algorithm against several baseline methods for estimating optimal transport maps on the sci-Plex single-cell RNA sequencing dataset. The comparison is done using the Sinkhorn divergence (DɛD) as the evaluation metric, calculated with the ℓ2 transport cost. The table shows the average Sinkhorn divergence values and standard errors for each method across five different runs on data from three different cell lines treated with different drugs, at various dimensions (16, 64, 256). The ‘5-drug rank’ column indicates the relative performance of the methods across all five drugs considered.
read the caption
Table 1: Performance of PROGOT compared to baselines, w.r.t DɛD between source and target of the sci-Plex dataset. Reported numbers are the average of 5 runs, together with the standard error.
In-depth insights#
Entropic OT Limits#
Entropic Optimal Transport (EOT) offers a robust approach to solving optimal transport problems, particularly for large datasets. However, the choice of the regularization parameter (ε) in EOT significantly impacts its performance, influencing computational speed, statistical accuracy, and the inherent bias of the resulting transport plan or map. Understanding the effects of ε is crucial for reliable applications of EOT. Small ε values can lead to slow convergence and numerical instability, while large values introduce bias and blur the transport plan, potentially masking important structural information. Therefore, the ‘Entropic OT Limits’ refer to the trade-offs between these competing factors. Adaptive methods, such as dynamically scheduling ε during the optimization process, aim to mitigate these issues, finding the optimal balance between speed and accuracy. Research in this area focuses on both theoretical analysis of EOT’s behavior with varying ε, as well as developing more sophisticated algorithmic strategies for robust and efficient EOT computations.
PROGOT Algorithm#
The PROGOT algorithm presents a novel approach to solving entropic optimal transport (EOT) problems. Instead of directly solving the EOT problem in one step, it iteratively refines the solution by progressively moving the source distribution closer to the target distribution via a McCann interpolation. This progressive approach leverages Sinkhorn’s algorithm at each step, using a dynamically scheduled regularization parameter (ε) and step size (α). This adaptive scheduling addresses the well-known challenges of hyperparameter tuning in standard EOT solvers. The method is proven to yield a statistically consistent estimator, with experimental results suggesting that PROGOT outperforms traditional EOT and neural network methods in terms of speed and robustness, particularly for large-scale problems. The dynamic approach of PROGOT, by decomposing the transport problem, offers enhanced stability and resilience to poor parameter choices, potentially making it more suitable for practical applications.
Progressive EOT#
Progressive Entropic Optimal Transport (EOT) presents a novel approach to solving optimal transport problems by iteratively refining the transport plan. Instead of a single, potentially ill-conditioned optimization, PROGOT leverages a sequence of smaller EOT problems. Each step progressively moves the source distribution closer to the target, making each subproblem easier to solve and less sensitive to hyperparameter tuning, particularly the regularization parameter epsilon. This progressive scheme allows for more robust and efficient computation, even outperforming neural network-based methods in certain scenarios. The method cleverly incorporates ideas from dynamic optimal transport, using McCann interpolation to guide the iterative refinement. Theoretical guarantees establish the statistical consistency of the resulting map estimator. Overall, PROGOT offers a significant advancement in EOT, providing a faster, more reliable, and easier-to-tune alternative for large-scale applications.
Map Estimation#
The concept of map estimation in the context of optimal transport (OT) involves learning a function that maps points from a source distribution to a target distribution. Entropic Optimal Transport (EOT), a popular technique for solving OT problems, is often used in map estimation because of its computational efficiency and robustness. However, the performance of EOT can be sensitive to the choice of the regularization parameter, epsilon (ε). Progressive EOT (PROGOT) offers a novel approach, addressing the limitations of EOT by dynamically scheduling epsilon, leading to more robust and faster map estimation, particularly at large scales. PROGOT leverages a time discretization and a progressive approach, where successive OT problems are solved with updated parameters, effectively moving the source distribution toward the target incrementally. The method shows improved statistical properties, proving its consistency in map estimation under standard assumptions. PROGOT also demonstrates superior performance compared to other methods, including neural network based approaches, in terms of speed and accuracy.
Scalability & Scope#
The scalability and scope of the research are significant strengths. The authors demonstrate the algorithm’s effectiveness on large-scale datasets, such as the CIFAR-10 dataset with 60,000 images and high dimensionality (d = 1024), showcasing its ability to handle real-world problems beyond typical single-cell datasets. PROGOT’s performance on this scale is remarkable, given the computational challenges of optimal transport. This broad applicability extends the practical impact of the research, moving beyond the niche field of single-cell analysis to potentially broader machine learning applications. The ability to work with varied dimensions (16, 64, 256) also highlights the algorithm’s flexibility, and the consistent improvement in accuracy over baselines suggests the potential for meaningful impact. The provided theoretical guarantees on consistency add further weight to the claim of broader applicability and scalability. However, future work could explore even larger datasets and higher dimensions to fully assess the scaling limits. Furthermore, a more detailed analysis of computational cost across different dataset sizes and dimensions could strengthen the claims about scalability.
More visual insights#
More on figures
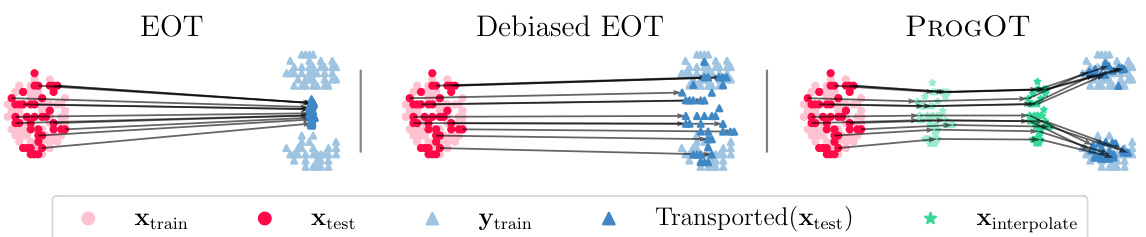
🔼 This figure compares three different optimal transport (OT) solvers: standard Entropic OT (EOT), debiased EOT, and the proposed Progressive Entropic OT (PROGOT). It shows how the choice of the regularization parameter (ε) significantly affects the quality of EOT solutions (left panel shows blurry couplings resulting from a poorly chosen ε), while debiased EOT only partially addresses this issue. The figure highlights that PROGOT overcomes these limitations by employing a progressive scheduling strategy which adapts the parameters during the OT computation, resulting in more robust and accurate couplings and map estimators (as demonstrated in the right panel).
read the caption
Figure 1: (left) EOT solvers collapse when the value of ε is not properly chosen. This typically results in biased map estimators and in blurry couplings (see Fig. 2 for the coupling matrix obtained between Xtrain and ytrain). (middle) Debiasing the output of EOT solvers can prevent a collapse to the mean seen in EOT estimators, but computes the same coupling. PROGOT (right) ameliorates these problems in various ways: by decomposing the resolution of the OT problem into multiple time steps, and using various forms of progressive scheduling, we recover both a coupling whose entropy can be tuned automatically and a map estimator that is fast and reliable.
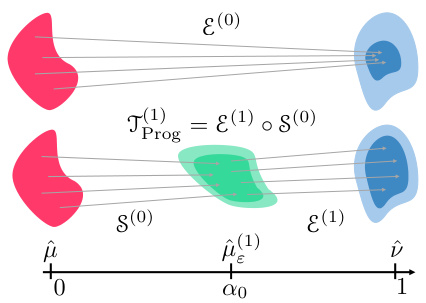
🔼 This figure illustrates the core idea behind the PROGOT algorithm. Instead of directly solving the optimal transport problem between the source and target distributions, PROGOT iteratively moves the source distribution closer to the target distribution along an estimated McCann interpolation path. Each step involves solving a smaller, better-conditioned optimal transport problem using entropic optimal transport (EOT) with a properly scheduled regularization parameter. This progressive approach reduces the sensitivity of the final solution to the choice of regularization parameter and makes the algorithm more stable and less prone to collapse.
read the caption
Figure 3: Intuition of PROGOT: By iteratively fitting to the interpolation path, the final transport step is less likely to collapse, resulting in more stable solver.
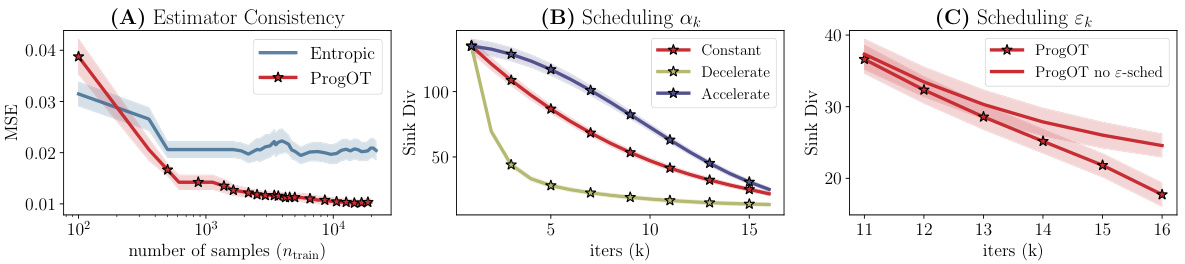
🔼 This figure presents three sub-figures that analyze different aspects of the proposed PROGOT algorithm. Subfigure (A) demonstrates the algorithm’s convergence to the true map by measuring the mean squared error (MSE) between the estimated map (TProg) and the ground truth map (T0) as the number of training samples increases. Subfigure (B) investigates the effect of different scheduling strategies for the parameter αk (step length in the McCann interpolation) on the Sinkhorn divergence (a measure of dissimilarity between probability distributions) between the iteratively refined source distribution and the target distribution. Finally, Subfigure (C) examines the influence of Algorithm 4 (an automatic scheduling method for the regularization parameter εk) on the Sinkhorn divergence during the iterative process.
read the caption
Figure 4: (A) Convergence of TProg to the ground-truth map w.r.t. the empirical L2 norm, for d = 4. (B) Effect of scheduling αk, for d = 64. (C) Effect of scheduling εk using Algorithm 4, for d = 64.
🔼 This figure demonstrates the performance of the PROGOT algorithm in learning the optimal transport map (TProg). Panel A shows the convergence of TProg to the ground truth map as the number of training samples increases. Panel B illustrates the impact of different scheduling strategies for the αk parameter on the algorithm’s performance, showing that the constant-speed schedule yields the best results. Finally, Panel C compares PROGOT with and without scheduling of the εk parameter, highlighting the effectiveness of Algorithm 4 in setting the regularization parameter.
read the caption
Figure 4: (A) Convergence of TProg to the ground-truth map w.r.t. the empirical L2 norm, for d = 4. (B) Effect of scheduling αk, for d = 64. (C) Effect of scheduling εk using Algorithm 4, for d = 64.

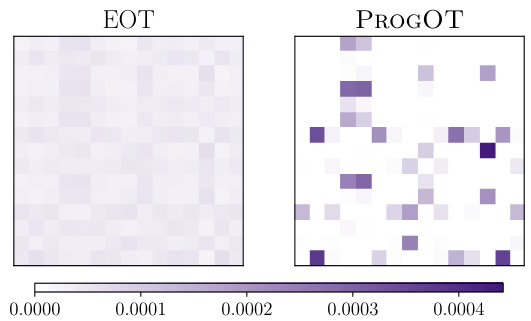
🔼 This figure shows an example of the optimal assignment problem between CIFAR images and their blurred versions. The left side shows example images of CIFAR and their blurred counterparts (σ = 4). The middle shows the optimal coupling matrix (P*) which should be an identity matrix if the cost is l2 norm. The right side shows the coupling matrix (P) computed using PROGOT (K=4, constant speed schedule). The results demonstrate PROGOT’s ability to recover the nearly optimal coupling in this large-scale problem.
read the caption
Figure 6: We consider the optimal assignment problem between all CIFAR images and their blurry CIFAR as trace, and KL divergence from counterparts using the l2 loss. A small subset of 3 original images on the left can be compared with their blurred counterpart on the right, with σ = 4. PROGOT is run for K = 4 and with the constant-speed schedule.

🔼 This figure shows an example of an original CIFAR10 image and its blurred versions with blur parameters σ = 2 and σ = 4. The goal is to match these blurry images back to their original counterparts, which will serve as a benchmark for large-scale optimal transport experiments. The optimal coupling for this task (using the L2 cost function), is the identity matrix; this is because each image must be matched to its blurred counterpart. This experiment is important because it allows for an objective assessment of the performance of different algorithms in a large-scale optimal transport problem where the true solution is known.
read the caption
Figure 7: Example of a CIFAR10 image and blurred variant. We match blurry images to the originals.
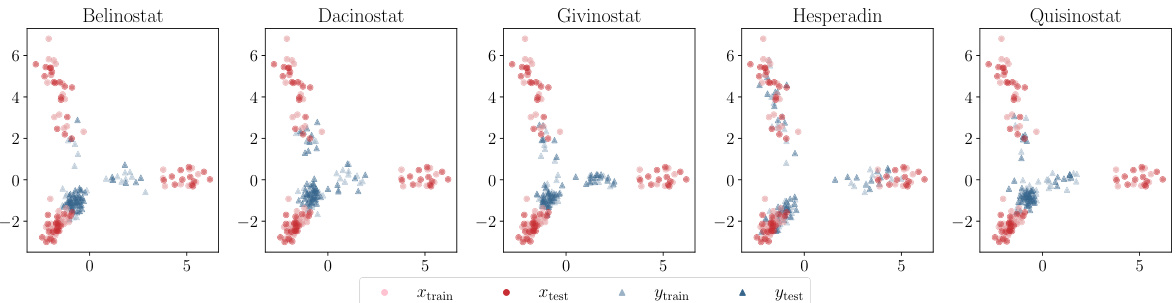
🔼 This figure visualizes the single-cell RNA sequencing data from Srivatsan et al. (2020). It uses principal component analysis (PCA) to reduce the dimensionality of the data to two dimensions, focusing on 50 samples for better visualization. The plot shows two distinct point clouds: one representing control cells (Xtrain, Xtest) and another representing cells perturbed by a specific drug (ytrain, ytest). The figure illustrates how the drug treatment affects the distribution of the cells in the reduced dimensional space.
read the caption
Figure 8: Overview of the single cell dataset Srivatsan et al. [2020]. We show the first two PCA dimensions performed on the training data, and limit the figure to 50 samples. The point cloud (Xtrain, Xtest) shows the control cells and (ytrain, ytest) are the perturbed cells using a specific drug.
🔼 This figure demonstrates the convergence and impact of scheduling parameters on PROGOT’s performance. (A) shows the mean squared error (MSE) between PROGOT’s estimated map and the ground truth map, showing convergence as the number of training samples increases. (B) compares different scheduling strategies for the step size parameter (αk), showing the effect on the Sinkhorn divergence between intermediate point clouds and the target distribution. (C) illustrates the effect of scheduling the regularization parameter (εk) using Algorithm 4, comparing it to a scenario without automatic scheduling. The results highlight the robustness and efficiency gains achieved by PROGOT’s progressive scheduling.
read the caption
Figure 4: (A) Convergence of TProg to the ground-truth map w.r.t. the empirical L2 norm, for d = 4. (B) Effect of scheduling αk, for d = 64. (C) Effect of scheduling εk using Algorithm 4, for d = 64.
🔼 The figure shows a comparison of three optimal transport (OT) solvers: EOT, Debiased EOT, and PROGOT. EOT solvers are prone to collapse and produce biased results when the regularization parameter ε is not chosen carefully. Debiasing helps, but doesn’t solve the core problem of instability. PROGOT, the proposed method, addresses these issues by breaking the OT problem into smaller sub-problems solved sequentially with progressively scheduled parameters. This leads to a more robust and efficient algorithm that produces better couplings and maps.
read the caption
Figure 1: (left) EOT solvers collapse when the value of ε is not properly chosen. This typically results in biased map estimators and in blurry couplings (see Fig. 2 for the coupling matrix obtained between Xtrain and ytrain). (middle) Debiasing the output of EOT solvers can prevent a collapse to the mean seen in EOT estimators, but computes the same coupling. PROGOT (right) ameliorates these problems in various ways: by decomposing the resolution of the OT problem into multiple time steps, and using various forms of progressive scheduling, we recover both a coupling whose entropy can be tuned automatically and a map estimator that is fast and reliable.
🔼 Figure 4 presents the experimental results to demonstrate the performance of PROGOT. (A) shows the convergence of the progressive entropic map estimator (TProg) towards the ground truth map as the number of training samples increases. (B) and (C) illustrate the impact of scheduling parameters αk and εk respectively on the performance of PROGOT. The results indicate that PROGOT is robust and efficient in estimating optimal transport maps.
read the caption
Figure 4: (A) Convergence of TProg to the ground-truth map w.r.t. the empirical L2 norm, for d = 4. (B) Effect of scheduling αk, for d = 64. (C) Effect of scheduling εk using Algorithm 4, for d = 64.

🔼 This figure compares three different optimal transport (OT) solvers: EOT, Debiased EOT, and PROGOT. EOT solvers suffer from instability and bias when the regularization parameter ε is not properly chosen, resulting in blurry couplings and inaccurate map estimators. Debiasing EOT improves the accuracy of the map estimator, but doesn’t affect the coupling’s quality. PROGOT, in contrast, addresses the issues through progressive scheduling and time discretization, yielding a more robust and faster approach with a tunable entropy coupling and reliable map estimator.
read the caption
Figure 1: (left) EOT solvers collapse when the value of ε is not properly chosen. This typically results in biased map estimators and in blurry couplings (see Fig. 2 for the coupling matrix obtained between Xtrain and ytrain). (middle) Debiasing the output of EOT solvers can prevent a collapse to the mean seen in EOT estimators, but computes the same coupling. PROGOT (right) ameliorates these problems in various ways: by decomposing the resolution of the OT problem into multiple time steps, and using various forms of progressive scheduling, we recover both a coupling whose entropy can be tuned automatically and a map estimator that is fast and reliable.
🔼 This figure compares three different optimal transport solvers: standard Entropic Optimal Transport (EOT), debiased EOT, and the proposed Progressive Entropic Optimal Transport (PROGOT). The left panel shows how standard EOT suffers from a collapse to the mean when the regularization parameter (ε) isn’t carefully chosen, leading to poor map estimation and blurry couplings. The middle panel shows that while debiased EOT addresses the collapse issue, it still suffers from the same coupling limitation. The right panel illustrates how PROGOT overcomes these limitations via a time-discretized approach, dynamically scheduled parameters, and the use of progressive scheduling resulting in improved coupling and map estimation.
read the caption
Figure 1: (left) EOT solvers collapse when the value of ε is not properly chosen. This typically results in biased map estimators and in blurry couplings (see Fig. 2 for the coupling matrix obtained between Xtrain and ytrain). (middle) Debiasing the output of EOT solvers can prevent a collapse to the mean seen in EOT estimators, but computes the same coupling. PROGOT (right) ameliorates these problems in various ways: by decomposing the resolution of the OT problem into multiple time steps, and using various forms of progressive scheduling, we recover both a coupling whose entropy can be tuned automatically and a map estimator that is fast and reliable.
🔼 The figure compares three approaches for solving the Entropic Optimal Transport (EOT) problem: standard EOT, debiased EOT, and the proposed PROGOT method. Standard EOT suffers from sensitivity to the regularization parameter (ε), leading to biased estimates and blurry couplings when ε is poorly chosen. Debiasing mitigates bias but doesn’t improve speed. PROGOT addresses these issues by breaking down the problem into smaller steps with progressively adjusted parameters, leading to faster, more robust computation of both couplings and maps.
read the caption
Figure 1: (left) EOT solvers collapse when the value of ε is not properly chosen. This typically results in biased map estimators and in blurry couplings (see Fig. 2 for the coupling matrix obtained between Xtrain and ytrain). (middle) Debiasing the output of EOT solvers can prevent a collapse to the mean seen in EOT estimators, but computes the same coupling. PROGOT (right) ameliorates these problems in various ways: by decomposing the resolution of the OT problem into multiple time steps, and using various forms of progressive scheduling, we recover both a coupling whose entropy can be tuned automatically and a map estimator that is fast and reliable.
More on tables

🔼 This table compares the performance of the proposed PROGOT algorithm to several baseline methods for estimating optimal transport maps. The comparison is done using the Sinkhorn divergence (DɛD) as a metric, which measures the distance between two probability distributions. The sci-Plex dataset, a single-cell RNA sequencing dataset, is used for the evaluation. The table shows the results for different dimensionality reduction methods (dPCA) and the different algorithms across various drugs, demonstrating PROGOT’s improved performance.
read the caption
Table 1: Performance of PROGOT compared to baselines, w.r.t DɛD between source and target of the sci-Plex dataset. Reported numbers are the average of 5 runs, together with the standard error.

🔼 This table compares the performance of the proposed PROGOT algorithm against several baseline methods for single-cell RNA sequencing data. The performance metric used is the Sinkhorn divergence (D&D), which measures the distance between the source and target distributions after applying the different transport methods. The table shows the average Sinkhorn divergence and its standard error for three different dimensionality reduction levels (d = 16, 64, 256) and five different drugs. Lower values of D&D indicate better alignment between the source and target.
read the caption
Table 1: Performance of PROGOT compared to baselines, w.r.t D&D between source and target of the sci-Plex dataset. Reported numbers are the average of 5 runs, together with the standard error.

🔼 This table compares the performance of the PROGOT algorithm to four other baseline algorithms for map estimation on the sci-Plex single-cell RNA sequencing dataset. The performance is measured using the Sinkhorn divergence (D&D) between the source and target data, which quantifies the dissimilarity between the two distributions. The table shows the average Sinkhorn divergence and standard error for each algorithm across five different runs, for three different drug types and three dimensionality reduction values (dPCA). Lower values indicate better performance.
read the caption
Table 1: Performance of PROGOT compared to baselines, w.r.t D&D between source and target of the sci-Plex dataset. Reported numbers are the average of 5 runs, together with the standard error.
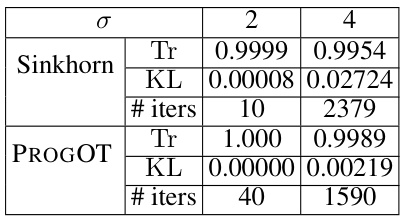
🔼 This table shows the performance of PROGOT and Sinkhorn algorithms in recovering the original coupling matrix from blurred images. The blur strength (sigma) is varied (2 and 4). The metrics used are the trace of the recovered coupling matrix (Tr), the Kullback-Leibler (KL) divergence from the true identity matrix, and the number of iterations (# iters) required by each algorithm. PROGOT uses K=4 iterations and a constant-speed schedule.
read the caption
Table 2: Coupling recovery, quantified as trace, and KL divergence from original identity matrix, for coupling matrices obtained with PROGOT and Sinkhorn, for coupling matrices obtained with PROGOT and Sinkhorn, for blur strengths σ = 2,4. PROGOT is run for K = 4 and with the constant-speed schedule.

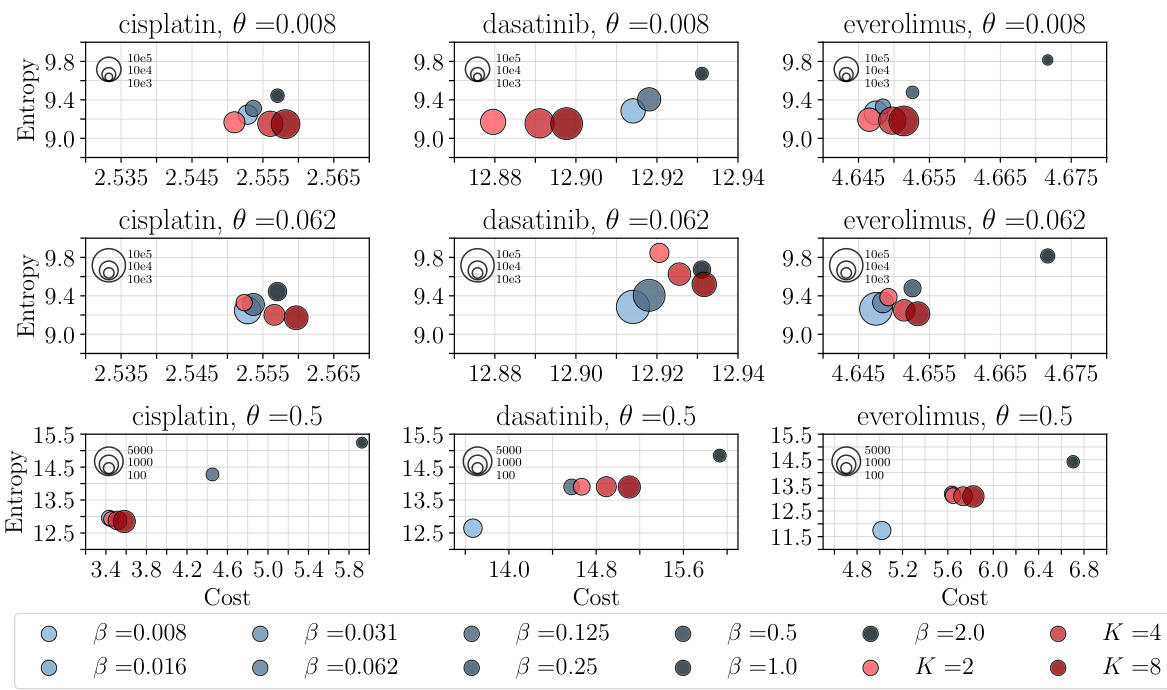
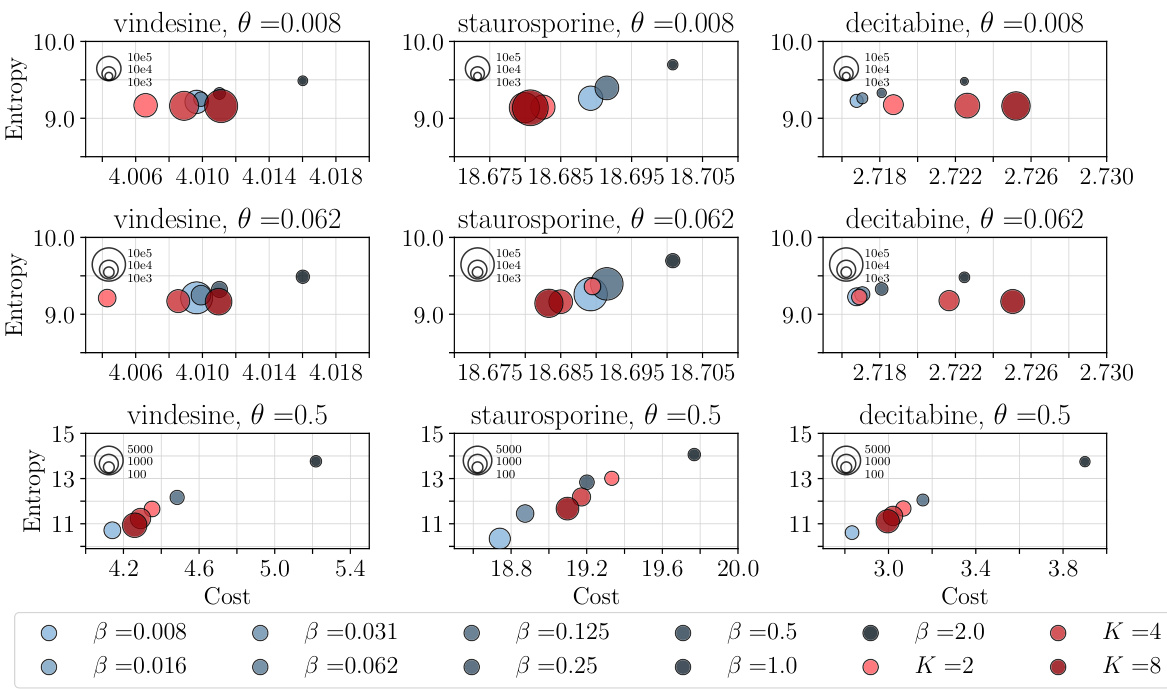
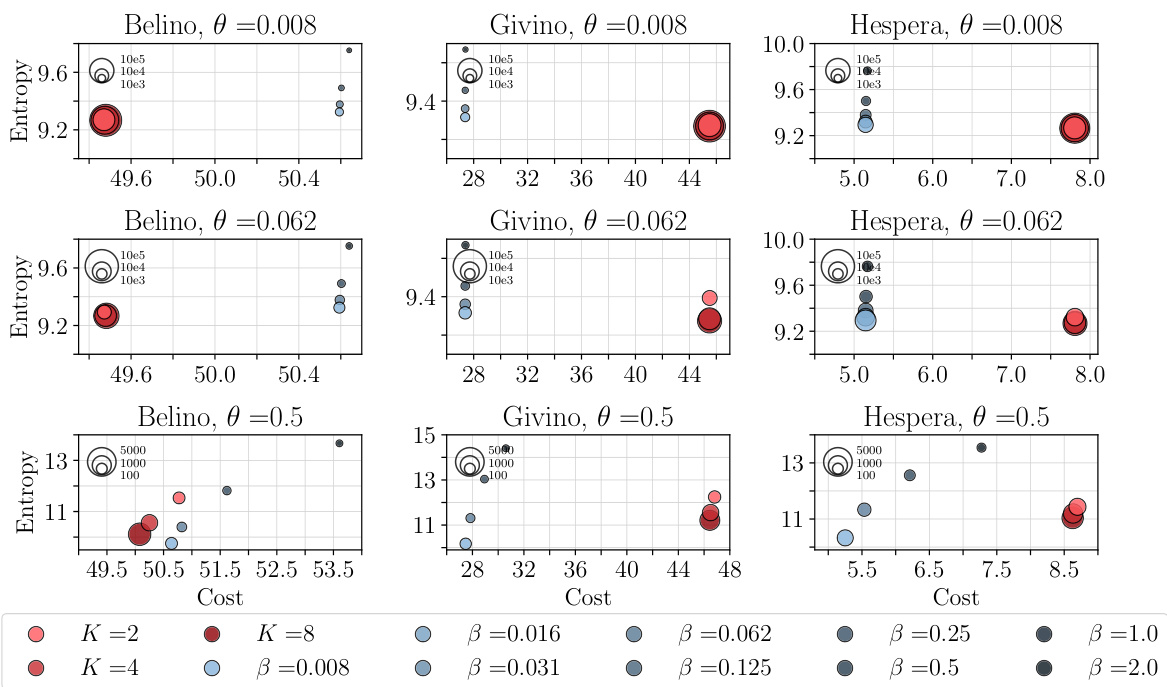
🔼 This table compares the performance of the PROGOT algorithm to other baseline methods for map estimation using the sci-Plex single-cell RNA sequencing dataset. The performance metric is the Sinkhorn divergence (D&D) between the source and target point clouds after applying the different map estimation methods. The table shows results for three different drugs (Belinostat, Givinostat, Hesperadin) and different dimensionality reduction (PCA) parameters (d = 16, 64, 256). The reported values are averages across 5 independent runs with standard errors.
read the caption
Table 1: Performance of PROGOT compared to baselines, w.r.t D&D between source and target of the sci-Plex dataset. Reported numbers are the average of 5 runs, together with the standard error.

🔼 This table compares the performance of the PROGOT algorithm to several baseline methods on the sci-Plex single-cell RNA sequencing dataset. The performance metric used is the Sinkhorn divergence (D&D), which measures the distance between two distributions. The table shows the average Sinkhorn divergence (and its standard error) for each algorithm across five runs for various dimensionality reduction techniques (d = 16, 64, and 256) and for five different drugs. Lower values indicate better performance in aligning source and target distributions.
read the caption
Table 1: Performance of PROGOT compared to baselines, w.r.t D&D between source and target of the sci-Plex dataset. Reported numbers are the average of 5 runs, together with the standard error.
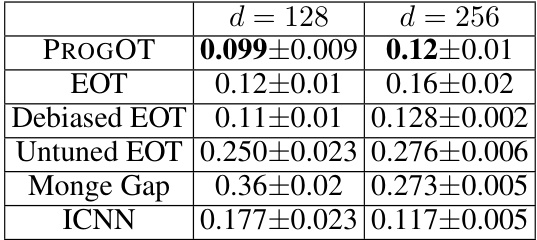
🔼 This table presents the mean squared error (MSE) results for comparing different optimal transport map estimation methods on a Gaussian Mixture Model (GMM) benchmark dataset. The MSE is calculated as the average of the squared Euclidean distances between estimated maps and ground truth maps for 500 test points. Different algorithms, including PROGOT, EOT, Debiased EOT, Untuned EOT, Monge Gap and ICNN are evaluated for their map estimation accuracy, with results provided for two dimensions (d=128 and d=256).
read the caption
Table 5: GMM benchmark. The Table shows the MSE, average of ||ŷitest||2 for ntest = 500 test points, where ŷ = T(xtest) and the ground truth is ytest.
Full paper#