TL;DR#
Offline reinforcement learning struggles with limited data and safety constraints; existing methods lack theoretical guarantees or robust performance. Many existing methods require strong assumptions on data coverage or lack robustness in hyperparameter settings.
WSAC, a novel algorithm, uses a two-player Stackelberg game to refine the objective function, optimizing the policy while adhering to safety constraints and addressing data limitations using importance weighting. It achieves optimal statistical convergence, and theoretical guarantees ensure safe policy improvement across various hyperparameter settings. Empirical results demonstrate WSAC’s superiority over existing methods.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel algorithm, WSAC, for safe offline reinforcement learning that offers robust policy improvement with theoretical guarantees and outperforms existing state-of-the-art methods. It addresses the crucial challenge of learning safe and effective policies with limited data, opening new avenues for research in safety-critical applications.
Visual Insights#

🔼 This figure compares the performance of the proposed WSAC algorithm against a baseline behavior policy in a tabular setting (simple MDP). The behavior policy is a mixture of a truly optimal policy and a completely random one. Different mixture percentages (20%, 50%, 80%) represent varying levels of competence in the baseline policy. The results demonstrate that WSAC reliably improves upon the baseline policy while staying within a defined safety threshold (cost ≤ 0.1), even when the behavior policy itself is unsafe (violating the cost threshold). This highlights WSAC’s ability to achieve safe policy improvement.
read the caption
Figure 1: Comparison between WSAC and the behavior policy in the tabular case. The behavior policy is a mixture of the optimal policy and a random policy, with the mixture percentage representing the proportion of the optimal policy. The cost threshold is set to 0.1. We observe that WSAC consistently ensures a safely improved policy across various scenarios, even when the behavior policy is not safe.
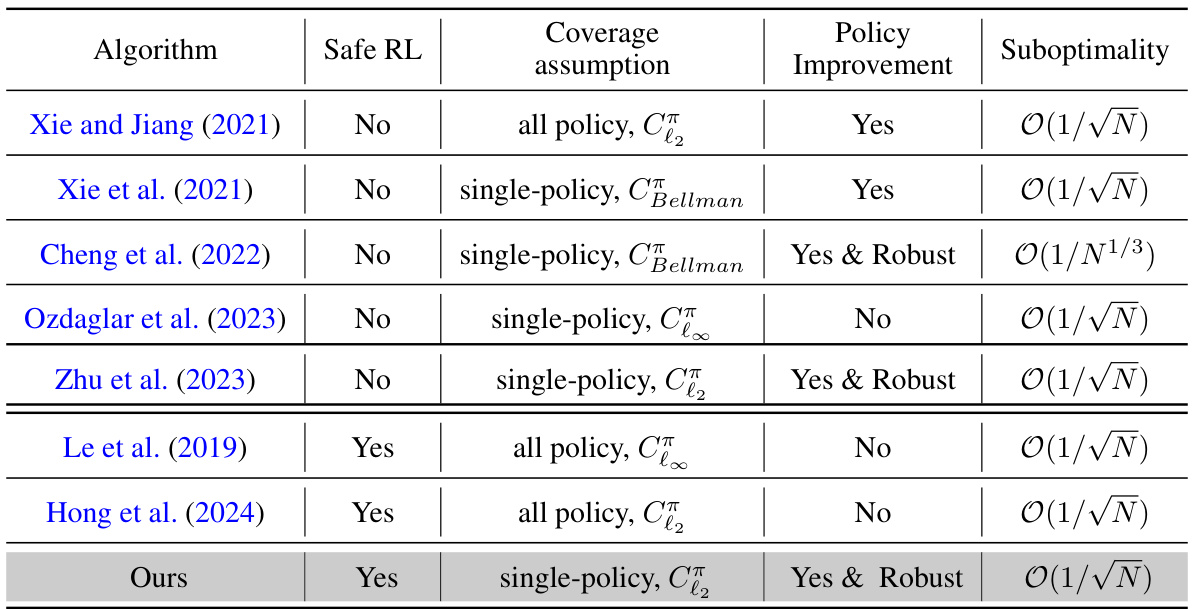
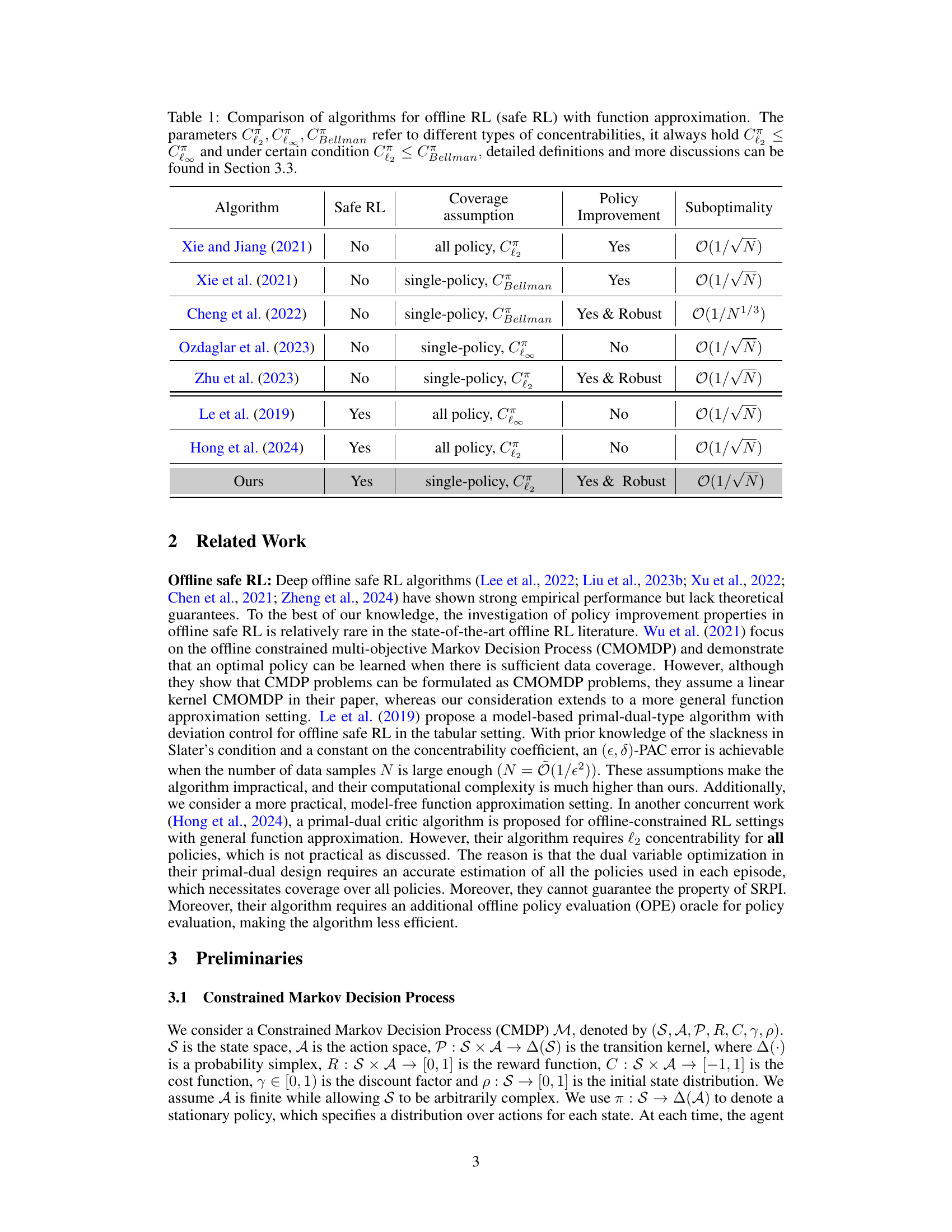
🔼 This table compares various offline reinforcement learning algorithms. It contrasts their ability to guarantee safe policy improvement, the assumptions made about data coverage (all-policy vs. single-policy concentrability), and their suboptimality bounds. The table highlights the differences in the theoretical guarantees and assumptions between the proposed WSAC algorithm and existing approaches.
read the caption
Table 1: Comparison of algorithms for offline RL (safe RL) with function approximation. The parameters C, C, CBellman refer to different types of concentrabilities, it always hold C≤C and under certain condition C2 ≤ CBellman, detailed definitions and more discussions can be found in Section 3.3.
In-depth insights#
Adversarial Training#
Adversarial training, in the context of machine learning, introduces a competitive framework where models are trained against an adversary, aiming to enhance robustness. This approach is particularly valuable in contexts like offline reinforcement learning, where data limitations and potential safety concerns are prominent. Adversarial training in this scenario often involves multiple agents (actor and critics) competing, leading to improved performance compared to standard methods. The adversary, typically one or more critics, focuses on identifying weaknesses in the actor’s policy. This iterative process improves the actor’s ability to handle challenging scenarios and perform consistently well, even with incomplete data or in unsafe conditions. A key benefit is the enhanced safety and robustness guarantees often achieved with this training approach. By forcing the model to confront and overcome adversarial challenges, adversarial training creates more robust policies than those trained via traditional methods.
Safe Offline RL#
Safe offline reinforcement learning (RL) tackles the challenges of learning safe policies from pre-collected data, eliminating the need for risky online exploration. This is crucial in real-world applications where direct interaction is expensive, dangerous, or simply impossible. The core difficulty lies in ensuring the learned policy remains safe—meeting predefined constraints—while simultaneously improving upon a pre-existing behavior policy. Robust policy improvement is a key goal, guaranteeing that the learned policy is at least as good as the original. Furthermore, research in this area often explores various concentrability assumptions related to the data coverage, striving for stronger theoretical guarantees with less restrictive requirements. Algorithmic advancements typically focus on addressing issues such as insufficient data coverage and ensuring that the learned policy outperforms the base policy both effectively and safely. This involves careful consideration of the underlying trade-off between policy improvement and safety constraints, often involving techniques like pessimism to handle uncertainty and adversarial training to make policies more robust. The field is actively advancing, creating more theoretically sound and practically effective methods to deliver reliable, safe RL in various domains.
Robust Policy Impr.#
The concept of “Robust Policy Improvement” in reinforcement learning centers on designing algorithms that reliably enhance a policy’s performance, especially when facing uncertainties or limitations in data or model assumptions. A robust algorithm should exhibit consistent improvement across various scenarios, even with noisy data, imperfect models, or a limited exploration of the state-action space. This robustness is particularly crucial in real-world applications where perfect knowledge is unrealistic and unexpected situations can occur. Key aspects of robust policy improvement include: guarantees on performance gains compared to a baseline policy, theoretical analysis to support claims of robustness, and empirical results showing reliable improvements across varied settings and datasets. Developing such algorithms involves techniques like pessimism in the face of uncertainty, careful regularization of learned models, and the incorporation of domain knowledge to constrain the solution space and guide the learning process. Robustness is not only about performance but also safety: if actions have consequences, an improvement that is only robust under limited circumstances might be unacceptable.
Single-Policy Focus#
A ‘Single-Policy Focus’ in offline reinforcement learning (RL) signifies a paradigm shift from traditional approaches that necessitate assumptions about all possible policies within a given environment. Instead, this approach concentrates on analyzing and optimizing a single, pre-selected policy, often a readily available behavior policy or an expert demonstration. This dramatically reduces computational complexity and data requirements, making offline RL more feasible for real-world applications with limited datasets. The core advantage lies in relaxing stringent concentrability assumptions, which are often difficult to satisfy in practice. By focusing on a single policy, the algorithm’s robustness and convergence guarantees become significantly stronger, yielding more reliable policy improvements. However, this focus also introduces limitations. The learned policy’s performance is heavily dependent on the quality of the initial single policy; a poor starting point would likely lead to suboptimal results. Furthermore, generalizability to unseen scenarios might be reduced compared to methods considering the entire policy space. Therefore, a single-policy strategy requires careful selection of the reference policy and consideration of potential tradeoffs between computational efficiency and overall performance.
Future Work#
The research paper’s ‘Future Work’ section would ideally explore extending the adversarial training framework to handle multi-agent settings and coupled constraints, enhancing the algorithm’s adaptability to more complex scenarios. Investigating the impact of different function approximation methods on the algorithm’s performance and robustness would provide valuable insights. Further theoretical analysis could focus on relaxing the single-policy concentrability assumption, striving for broader applicability. Empirical evaluations on a wider range of tasks and datasets are necessary to demonstrate the algorithm’s generalizability. Finally, exploring practical implementation improvements, such as efficient optimization strategies and hyperparameter tuning techniques, would enhance WSAC’s real-world applicability and impact.
More visual insights#
More on figures

🔼 This figure shows four different simulated environments used for evaluating the performance of the proposed WSAC algorithm and its baselines. * BallCircle: A circular track with a safety zone where an agent (a ball) must navigate in a clockwise direction, penalized for leaving the track. * CarCircle: Similar to BallCircle but the agent is a car. * PointButton: An agent (a point) must navigate to a goal button, avoiding obstacles (gremlins). * PointPush: The agent must push a box to a goal, again while avoiding obstacles.
read the caption
Figure 2: BallCircle and CarCircle (left), PointButton (medium), PointPush(right) .
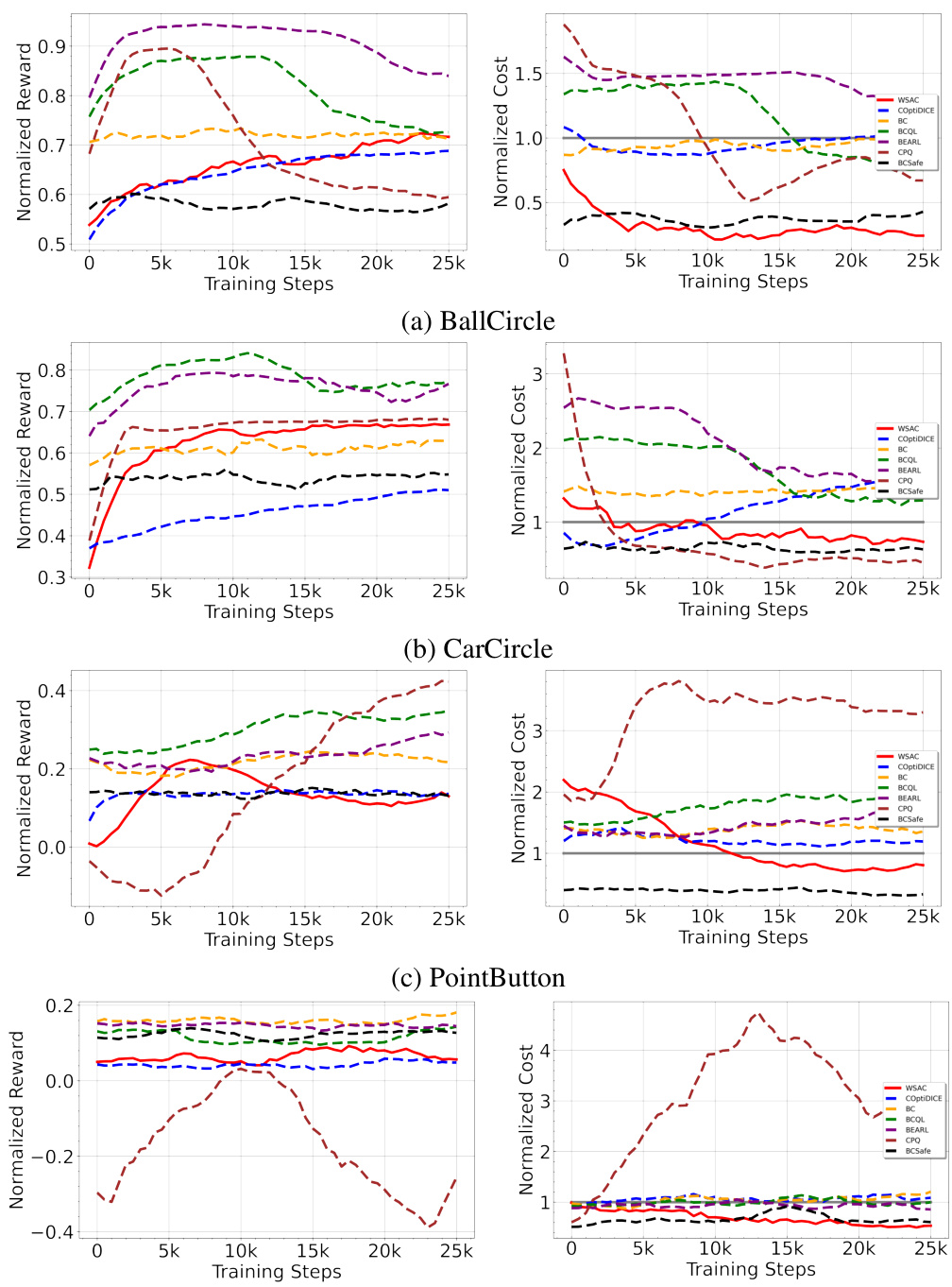
🔼 This figure shows the training curves of the proposed algorithm WSAC and several baselines on four different continuous control tasks: BallCircle, CarCircle, PointButton, and PointPush. Each curve represents the moving average of the normalized reward and cost over 20 evaluation episodes, calculated over three random seeds. The x-axis shows the training steps, and the y-axis shows the normalized reward and cost. A cost threshold of 1 is used; results below this threshold are considered safe. The figure demonstrates WSAC’s consistent performance across different tasks, achieving high rewards while maintaining safety (cost below 1).
read the caption
Figure 3: The moving average of evaluation results is recorded every 500 training steps, with each result representing the average over 20 evaluation episodes and three random seeds. A cost threshold 1 is applied, with any normalized cost below 1 considered safe.
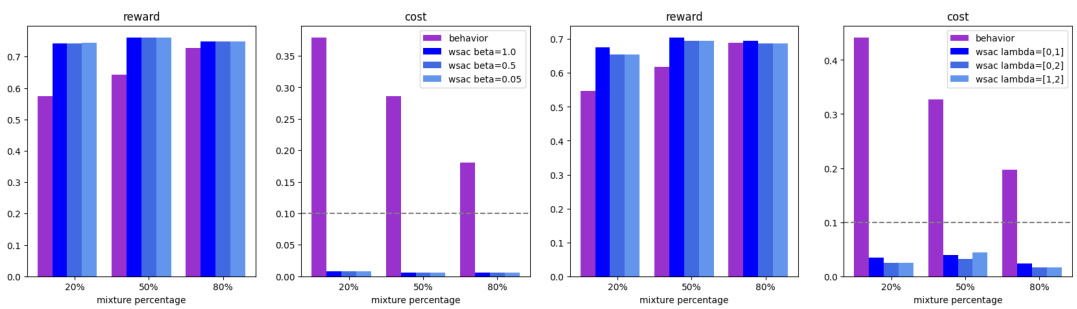
🔼 The figure shows the results of a comparison between the proposed WSAC algorithm and a baseline behavior policy in a tabular setting. The behavior policy is a mix of an optimal policy and a random policy, with varying proportions of the optimal policy. The x-axis represents the percentage of the optimal policy in the mixture. The y-axis displays both the reward and cost achieved by both policies. The cost threshold is set at 0.1. The plot illustrates that WSAC consistently outperforms the behavior policy while maintaining a safe level of cost, even when the behavior policy itself is unsafe.
read the caption
Figure 1: Comparison between WSAC and the behavior policy in the tabular case. The behavior policy is a mixture of the optimal policy and a random policy, with the mixture percentage representing the proportion of the optimal policy. The cost threshold is set to 0.1. We observe that WSAC consistently ensures a safely improved policy across various scenarios, even when the behavior policy is not safe.
More on tables

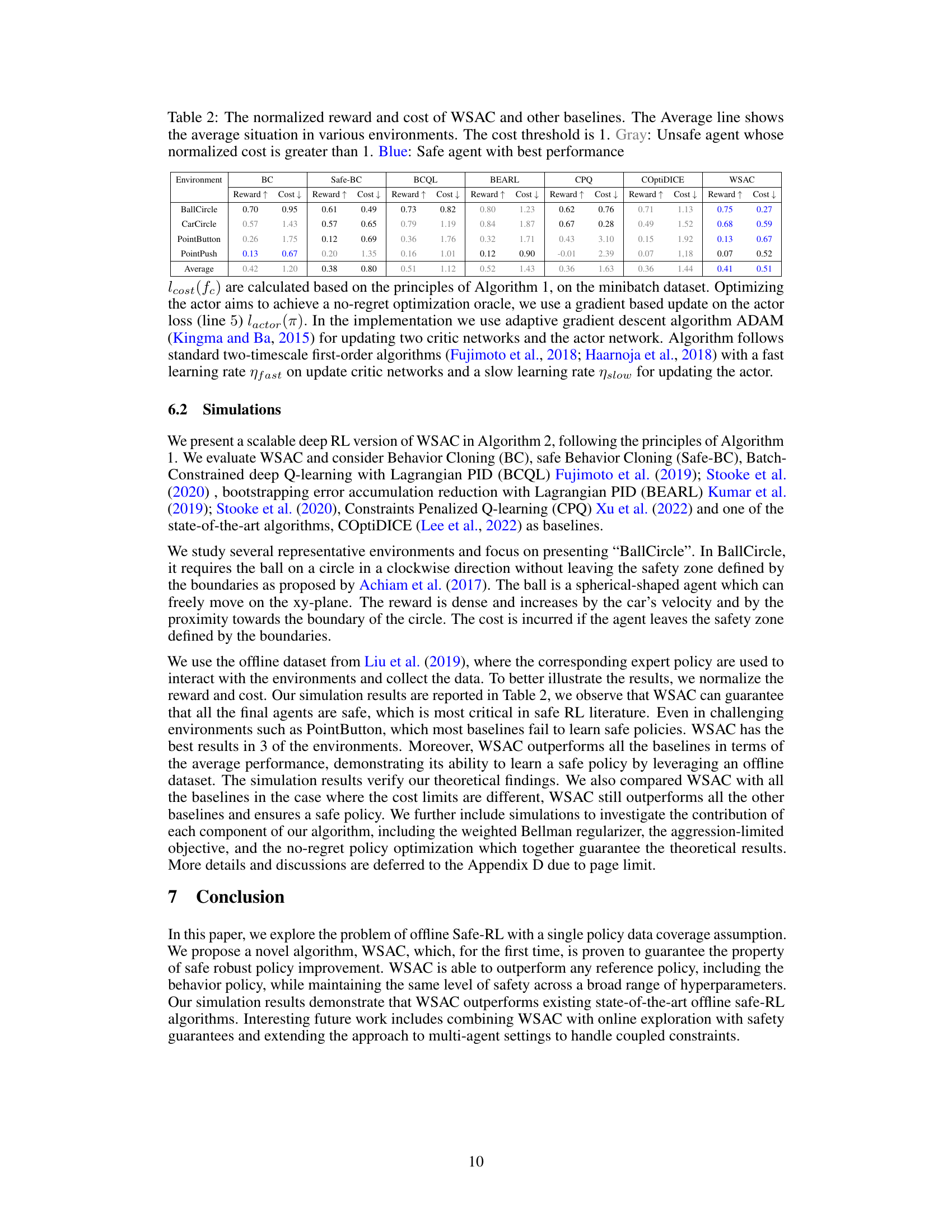
🔼 This table presents a comparison of the performance of the proposed WSAC algorithm against several baseline algorithms across four continuous control environments. The metrics used are the normalized reward (higher is better) and the normalized cost (lower is better). A cost threshold of 1 is used to define a safe policy (cost ≤ 1). The table highlights which algorithms produced safe policies (in blue) and unsafe policies (in gray), and provides a summary of the average performance across all environments.
read the caption
Table 2: The normalized reward and cost of WSAC and other baselines. The Average line shows the average situation in various environments. The cost threshold is 1. Gray: Unsafe agent whose normalized cost is greater than 1. Blue: Safe agent with best performance
🔼 This table compares several algorithms for offline reinforcement learning, specifically focusing on safe reinforcement learning with function approximation. It contrasts the algorithms based on whether they are designed for safe RL, the type of concentrability assumption used (all-policy or single-policy), whether they guarantee policy improvement, and their suboptimality rate. The table highlights that the proposed WSAC algorithm offers the unique combination of being designed for safe RL, using only single-policy concentrability assumptions, guaranteeing policy improvement, and having an optimal suboptimality rate.
read the caption
Table 1: Comparison of algorithms for offline RL (safe RL) with function approximation. The parameters C∞, C, CBellman refer to different types of concentrabilities, it always hold C∞ ≤ C and under certain condition C2 ≤ CBellman, detailed definitions and more discussions can be found in Section 3.3.

🔼 This table presents a comparison of the normalized reward and cost achieved by WSAC and several other baseline algorithms across four different continuous control environments. The ‘Average’ row provides an aggregated view of the performance across all environments. The cost threshold of 1 is used to classify agents as either safe (normalized cost ≤ 1, indicated in blue) or unsafe (normalized cost > 1, indicated in gray). The table highlights WSAC’s superior performance in achieving both high reward and safety.
read the caption
Table 2: The normalized reward and cost of WSAC and other baselines. The Average line shows the average situation in various environments. The cost threshold is 1. Gray: Unsafe agent whose normalized cost is greater than 1. Blue: Safe agent with best performance

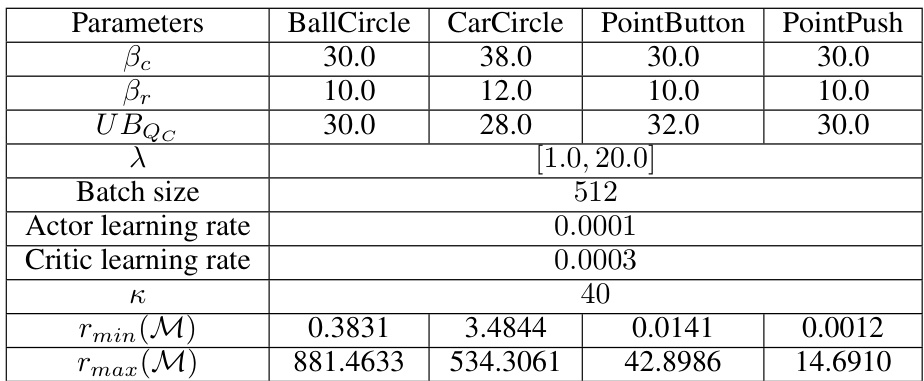
🔼 This table presents the results of an ablation study conducted to evaluate the contribution of each component of the WSAC algorithm in a tabular setting with a cost limit of 0.1. The study involved 10 repeated experiments for each configuration. The components evaluated include the no-regret policy optimization, the aggression-limited objective, and the weighted Bellman regularizer. The table shows the average cost and reward obtained for each configuration, illustrating the impact of each component on the overall performance.
read the caption
Table 5: Ablation study under tabular case (cost limit is 0.1) over 10 repeat experiments
Full paper#