TL;DR#
Bayesian deep learning often struggles with accurately quantifying uncertainty and incorporating prior knowledge effectively. Current methods often rely on weight-space priors, which are computationally expensive and lack interpretability, particularly in deep networks. The use of isotropic Gaussian priors, while computationally tractable, can lead to pathological behavior as network depth increases.
FSP-LAPLACE tackles these issues by directly placing a prior on function space, using a Gaussian Process (GP). This allows for the incorporation of structured and interpretable inductive biases like smoothness, periodicity, or length scales. The authors recast training as finding the weak mode of the posterior measure, applying a Laplace approximation after model linearization. This is computationally efficient, leveraging matrix-free linear algebra. FSP-LAPLACE shows improved results on tasks where prior knowledge is readily available and stays competitive on standard black-box learning tasks.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in Bayesian deep learning and related fields because it presents a novel and efficient method for incorporating interpretable prior knowledge into deep neural networks, improving uncertainty quantification and generalization. It directly addresses the limitations of existing methods by using function-space priors, opening new avenues for research in scientific machine learning and other areas where prior knowledge is abundant.
Visual Insights#

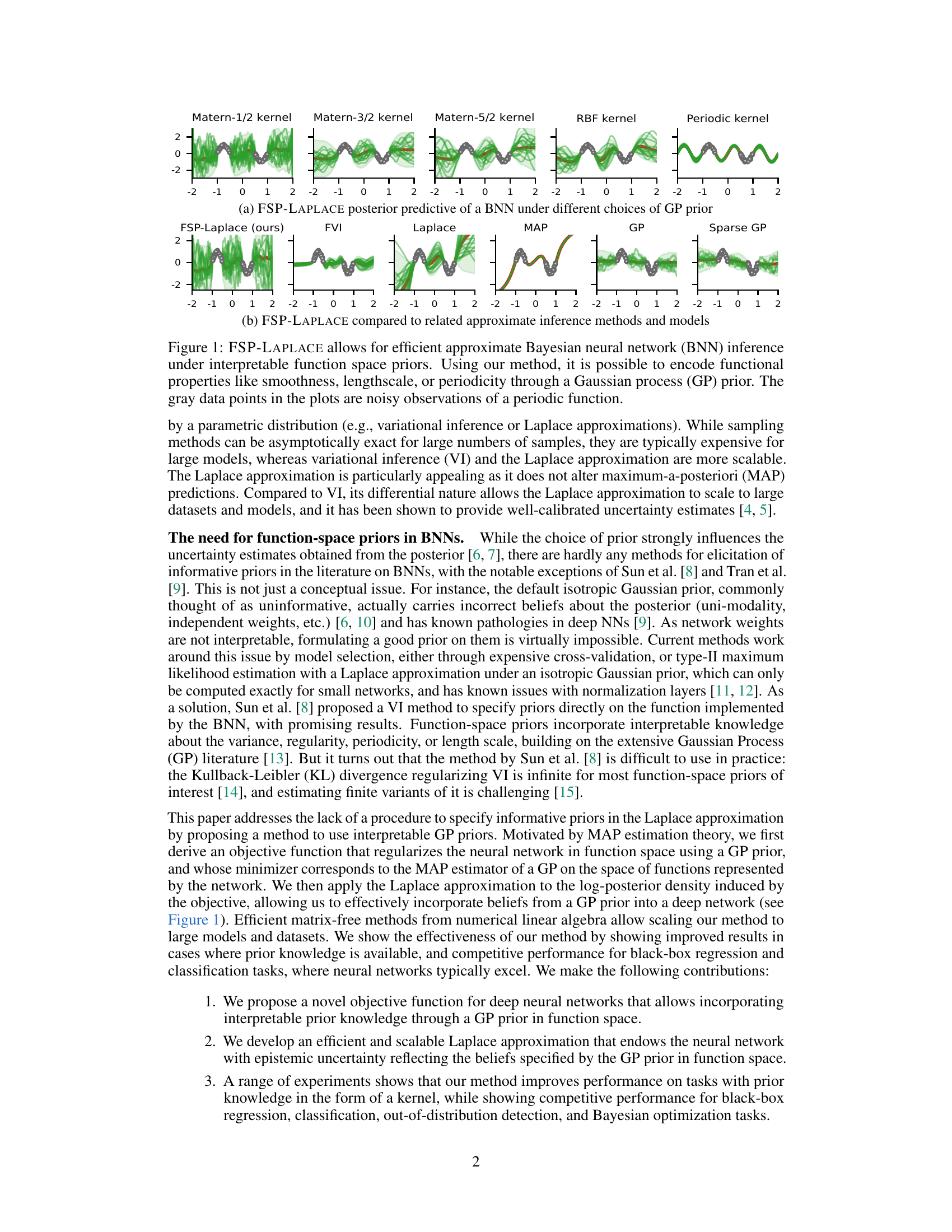
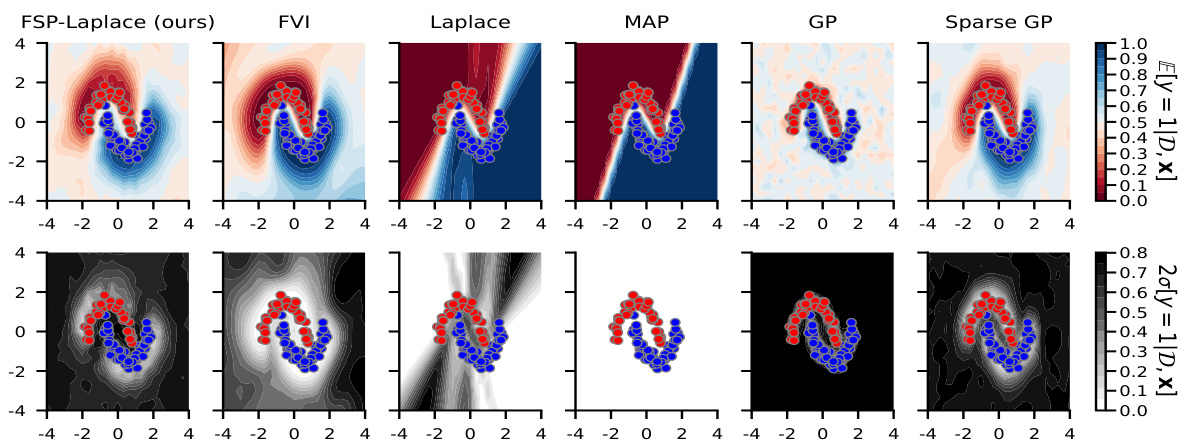
🔼 This figure compares the posterior predictive distribution of a Bayesian neural network (BNN) trained using the proposed FSP-LAPLACE method with different choices of Gaussian process (GP) priors. It shows how the method allows for efficient approximate Bayesian inference under interpretable function space priors, enabling the encoding of functional properties such as smoothness, length-scale, and periodicity through the GP prior. The plots also compare FSP-LAPLACE with other approximate inference methods and models, highlighting its effectiveness and ability to capture functional properties.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.
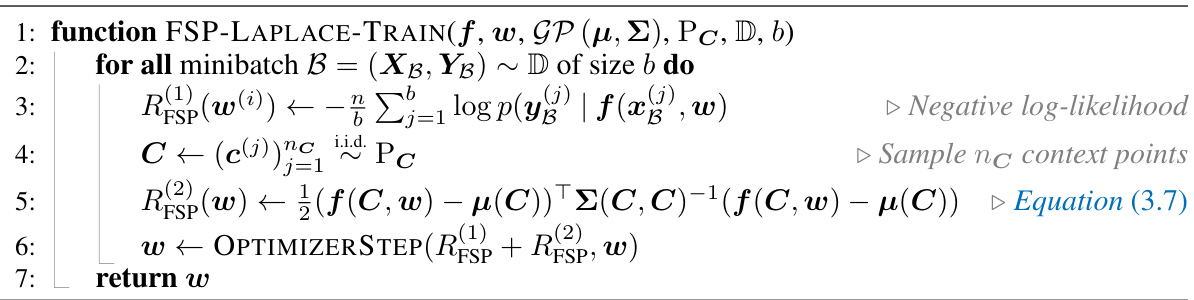
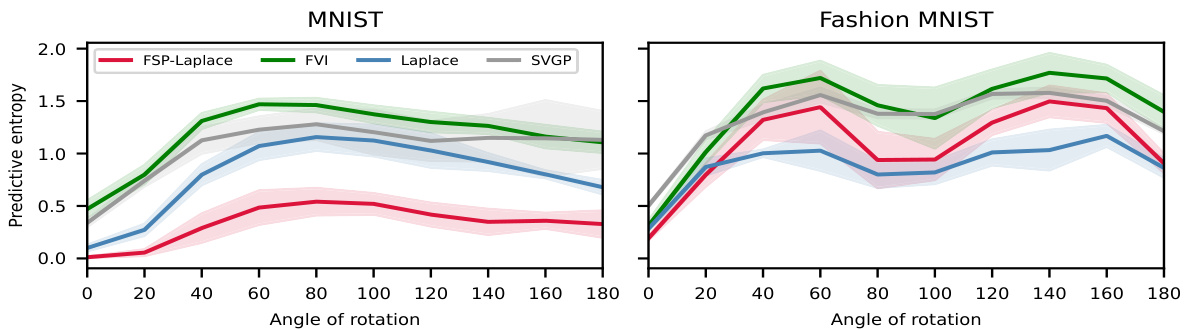
🔼 This table presents the quantitative results of the proposed FSP-LAPLACE method and several baselines on MNIST and FashionMNIST datasets. The metrics used for comparison include test expected log-likelihood, accuracy, expected calibration error (ECE), and out-of-distribution (OOD) detection accuracy. The results demonstrate that FSP-LAPLACE achieves competitive performance, matching or exceeding the accuracy of the best-performing baselines and showing superior performance in terms of expected log-likelihood and OOD detection.
read the caption
Table 2: Test expected log-likelihood, accuracy, expected calibration error and OOD detection accuracy on MNIST and FashionMNIST. FSP-LAPLACE performs strongly among baselines matching the accuracy of best-performing baselines and obtaining the highest expected log-likelihood and out-of-distribution detection accuracy.
In-depth insights#
FSP-Laplace: Overview#
FSP-Laplace offers a novel approach to Bayesian deep learning by directly incorporating prior knowledge into the function space, rather than the traditional weight space. This is particularly beneficial because it allows for the use of interpretable Gaussian process priors, which express structured inductive biases such as smoothness or periodicity. The method cleverly addresses the challenge of infinite-dimensional function spaces by framing training as a weak mode optimization problem. This enables efficient, scalable Laplace approximation using matrix-free linear algebra. The core innovation lies in its ability to combine the advantages of Laplace approximations (scalability, calibrated uncertainty) with the interpretability of GP priors. Overall, FSP-Laplace presents a significant step towards more interpretable and efficient Bayesian deep learning, especially for tasks where prior knowledge is readily available.
Function-Space Priors#
Function-space priors offer a powerful paradigm shift in Bayesian deep learning by directly placing priors on the function space, rather than on the model’s weights. This approach is particularly beneficial because weight space lacks interpretability, making it difficult to encode meaningful prior knowledge. Function space priors, often expressed using Gaussian processes (GPs), allow for the incorporation of intuitive properties like smoothness, periodicity, or length scales. This enables stronger inductive biases that can significantly improve generalization performance, especially when prior knowledge about the problem is available. However, the use of function-space priors presents computational challenges due to the infinite dimensionality of function spaces. The paper addresses these challenges by introducing a novel objective function that indirectly regularizes the neural network in function space and proposes a scalable method for approximating the posterior using matrix-free linear algebra. This approach makes it practical to apply function space priors in large models. The effectiveness of this method is validated through experiments on both synthetic and real-world datasets, showcasing improved performance compared to traditional weight-space priors.
Laplace Approximation#
The Laplace approximation, a cornerstone of Bayesian inference, offers a computationally efficient way to approximate intractable posterior distributions. By linearizing the model around the maximum a posteriori (MAP) estimate, it leverages a Gaussian approximation to capture the posterior’s shape. This approach is particularly attractive for Bayesian deep learning, where the high dimensionality of the parameter space renders exact Bayesian inference computationally prohibitive. Isotropic Gaussian priors are frequently used due to their mathematical tractability; however, this choice can lead to limitations in capturing complex posterior structures and may not effectively encode prior knowledge. The paper highlights a key limitation: the typical weight-space priors can result in a poor approximation of the true posterior, especially in deep networks. The core contribution lies in addressing this by employing function-space priors, directly placing priors on the function the network represents, which offers greater flexibility and interpretability. This shift allows for incorporating structured inductive biases and leads to improvements in capturing uncertainty, particularly when domain knowledge is available.
Empirical Evaluation#
An empirical evaluation section in a research paper would typically present the results of experiments designed to test the paper’s core claims. A thoughtful analysis would examine the choice of datasets, ensuring they’re representative and appropriately challenging. The evaluation metrics used should be carefully justified and relevant to the hypotheses. The section needs to provide sufficient detail for reproducibility, including model architectures, training procedures, hyperparameters, and the significance level of any statistical tests performed. Comparison to baselines is crucial for establishing the novel contribution’s improvement. A detailed breakdown of results, perhaps with tables and figures, is expected, and the discussion should interpret these results, acknowledging any limitations or unexpected findings. Addressing potential confounding factors and highlighting any sensitivity analyses would further strengthen the analysis. Finally, a strong conclusion summarizing the key findings and their implications would be important.
Future Work#
The paper’s lack of a dedicated ‘Future Work’ section is notable. However, several avenues for future research are implicitly suggested. Extending FSP-LAPLACE to handle more complex prior knowledge representations beyond basic kernels is crucial. Exploring different types of GP priors and developing efficient methods for eliciting these priors from domain experts are vital steps. Addressing the scalability limitations for very high-dimensional tasks should be prioritized, potentially by investigating alternative linear algebra techniques or developing more efficient approximations. Finally, a more rigorous theoretical analysis proving the convergence of weak modes and evaluating the effectiveness of the linearization approximation is warranted. A comparison with alternative methods for functional Bayesian inference is also recommended to solidify the method’s strengths and limitations.
More visual insights#
More on figures

🔼 This figure demonstrates the effectiveness of FSP-LAPLACE in performing Bayesian inference using interpretable function-space priors. It shows posterior predictive distributions obtained using different GP kernels (Matern 1/2, Matern 3/2, Matern 5/2, RBF, and Periodic), highlighting how FSP-LAPLACE successfully incorporates prior knowledge encoded in the chosen GP prior. The figure also compares FSP-LAPLACE’s performance with other approximate inference methods (Laplace, Full Variational Inference (FVI), Maximum a Posteriori (MAP), GP, and Sparse GP), showing that FSP-LAPLACE provides competitive performance while allowing for efficient and interpretable BNN inference.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.

🔼 This figure shows the posterior predictive distribution of a Bayesian neural network (BNN) trained using the proposed FSP-LAPLACE method with different Gaussian process (GP) priors. The top row demonstrates how different GP kernels (Matern 1/2, Matern 3/2, Matern 5/2, RBF, and Periodic) shape the posterior predictive. The bottom row compares the FSP-LAPLACE method to related methods like Full Variational Inference (FVI), Maximum A Posteriori (MAP) estimation, GP regression, and Sparse GP regression. The gray points represent noisy observations of a periodic function, highlighting how the different priors affect uncertainty estimation and prediction accuracy.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.
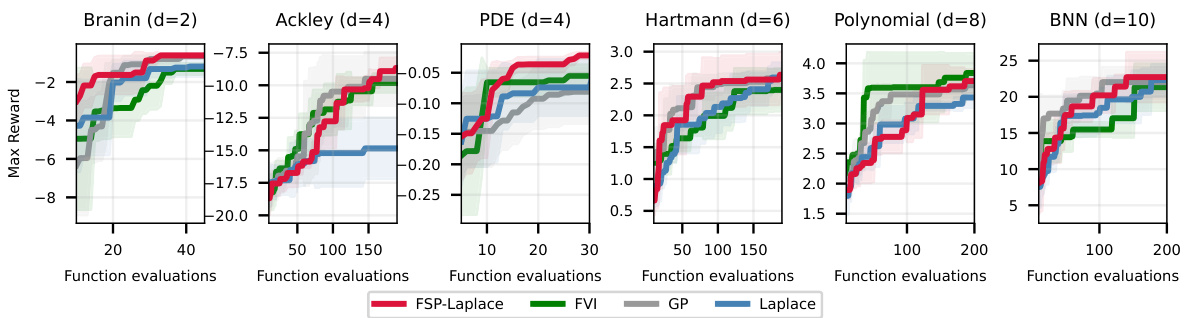
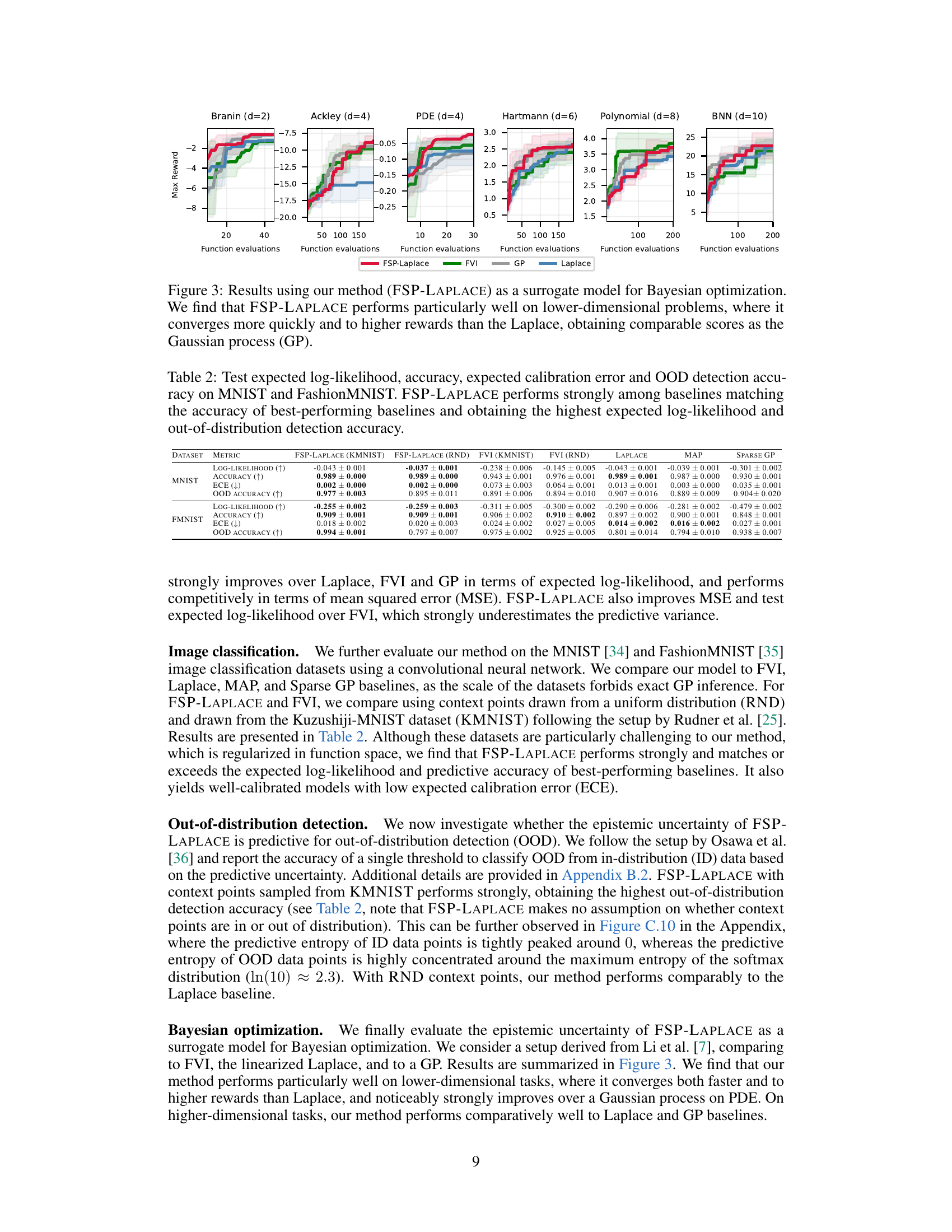
🔼 This figure compares the performance of FSP-LAPLACE against other Bayesian Optimization methods (FVI, Laplace, and GP) on six different test functions with varying dimensionality (2 to 10). The x-axis represents the number of function evaluations, while the y-axis shows the maximum reward achieved. FSP-LAPLACE demonstrates competitive or superior performance, especially in lower-dimensional settings, converging faster and achieving higher maximum rewards than Laplace, while matching GP’s performance in several cases.
read the caption
Figure 3: Results using our method (FSP-LAPLACE) as a surrogate model for Bayesian optimization. We find that FSP-LAPLACE performs particularly well on lower-dimensional problems, where it converges more quickly and to higher rewards than the Laplace, obtaining comparable scores as the Gaussian process (GP).

🔼 This figure compares the posterior predictive of a Bayesian neural network (BNN) trained using the proposed FSP-LAPLACE method with several other approximate inference methods and models. It highlights the ability of FSP-LAPLACE to incorporate interpretable function space priors in the form of a Gaussian process (GP) prior, demonstrating how different GP priors influence the resulting posterior distribution. The plots illustrate that FSP-LAPLACE can capture various functional properties, such as smoothness and periodicity, directly in function space, leading to improved uncertainty estimates. The gray data points represent noisy observations of a periodic function.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.

🔼 This figure shows the posterior predictive distribution of a Bayesian neural network (BNN) trained using the proposed FSP-LAPLACE method with different Gaussian process (GP) priors. It demonstrates the ability of FSP-LAPLACE to incorporate prior knowledge about the function (such as smoothness or periodicity) into the BNN’s predictions, resulting in more accurate and interpretable uncertainty estimates. The gray points represent noisy observations of the underlying function, while the green lines show samples from the posterior predictive distribution, and the red line is the mean prediction.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.

🔼 This figure shows the posterior predictive of a Bayesian neural network trained with FSP-LAPLACE under different choices of GP priors (RBF, periodic and Matern). The plots demonstrate how FSP-LAPLACE can incorporate prior knowledge about the function to be learned (e.g., smoothness, periodicity, lengthscale) directly into the model, leading to more accurate and informative uncertainty estimates. This is in contrast to traditional methods which often rely on less informative isotropic Gaussian priors in weight space.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.

🔼 The figure shows the results of applying the proposed FSP-LAPLACE method to a Bayesian neural network (BNN) with different Gaussian process (GP) priors. The top row illustrates how different GP priors (e.g., Matern kernels, RBF, periodic) influence the posterior predictive distribution of the BNN. The bottom row compares the FSP-LAPLACE results to other approximate inference methods such as Full Variational Inference (FVI), standard Laplace approximation, and GP/Sparse GP methods. The plots visualize how FSP-LAPLACE efficiently incorporates prior knowledge (encoded in the GP prior) to achieve accurate and well-calibrated uncertainty estimates.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.

🔼 This figure shows the posterior predictive distribution of a Bayesian neural network (BNN) trained with the proposed FSP-LAPLACE method, compared to several related approximate inference methods. The top row displays the posterior predictive of the BNN under various choices of GP prior, demonstrating the flexibility of the method in encoding functional properties like smoothness and periodicity. The bottom row compares the performance of FSP-LAPLACE to other methods such as full variational inference, Laplace approximation, and standard Gaussian processes, illustrating the competitive performance of FSP-LAPLACE.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.
🔼 This figure compares the performance of FSP-LAPLACE with other Bayesian neural network inference methods under different choices of GP priors. It shows posterior predictive distributions of a BNN for various choices of GP priors (different kernels), demonstrating the method’s ability to encode functional properties into the model. The plots show FSP-LAPLACE achieves competitive performance compared to other state-of-the-art methods.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.

🔼 This figure shows the posterior predictive distribution of a Bayesian neural network (BNN) trained with the proposed FSP-LAPLACE method, which uses function-space priors. The top row displays the predictive distribution under different choices of GP priors (kernels): Matern 1/2, Matern 3/2, Matern 5/2, RBF, and Periodic. The bottom row compares FSP-LAPLACE to other approximate inference methods: Laplace approximation, full variational inference (FVI), maximum a posteriori (MAP) estimation, a full Gaussian process (GP), and a sparse Gaussian process (sparse GP). Gray points are noisy observations, and the green lines represent samples from the posterior predictive distribution.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.

🔼 This figure compares the performance of FSP-LAPLACE against several baselines (FVI, Laplace, MAP, GP, Sparse GP) on the two-moons classification task. The key difference is that FSP-LAPLACE uses a Matern-1/2 covariance function as a prior. The figure shows that FSP-LAPLACE produces a rough decision boundary, similar to that produced by the Gaussian Process and sparse Gaussian Process, both of which also use the Matern-1/2 kernel. This indicates that FSP-LAPLACE successfully incorporates the prior information from the chosen kernel into the model’s predictions.
read the caption
Figure C.5: FSP-LAPLACE with a Matern-1/2 covariance function against baselines in the two-moons classification task. Similar to the Gaussian process (GP) and sparse GP, our method shows a rough decision boundary.
🔼 This figure compares the posterior predictive distribution of a Bayesian neural network (BNN) using different methods, including the proposed FSP-LAPLACE method. It highlights the ability of FSP-LAPLACE to incorporate prior knowledge about the underlying function (like smoothness or periodicity) using a Gaussian process prior, leading to improved results. The different plots show how various methods handle noisy observations of a periodic function, demonstrating FSP-LAPLACE’s superiority in capturing functional properties.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.

🔼 This figure shows the posterior predictive of a Bayesian neural network (BNN) using FSP-LAPLACE with different Gaussian process (GP) priors. It compares FSP-LAPLACE’s performance to other approximate inference methods, such as Full Variational Inference (FVI) and Laplace approximation, highlighting FSP-LAPLACE’s ability to incorporate structured prior knowledge about the function into the BNN inference process. The GP priors used demonstrate different functional properties (smoothness, periodicity, length scale) showing how FSP-LAPLACE allows for incorporating such prior knowledge.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.
🔼 This figure demonstrates the effectiveness of FSP-LAPLACE in performing approximate Bayesian inference for Bayesian neural networks. It highlights the use of interpretable function-space priors, specifically Gaussian process priors, to encode various functional properties (smoothness, length scale, periodicity). The figure showcases how the method handles noisy observations of a periodic function, illustrating its ability to incorporate prior knowledge effectively.
read the caption
Figure 1: FSP-LAPLACE allows for efficient approximate Bayesian neural network (BNN) inference under interpretable function space priors. Using our method, it is possible to encode functional properties like smoothness, lengthscale, or periodicity through a Gaussian process (GP) prior. The gray data points in the plots are noisy observations of a periodic function.
More on tables

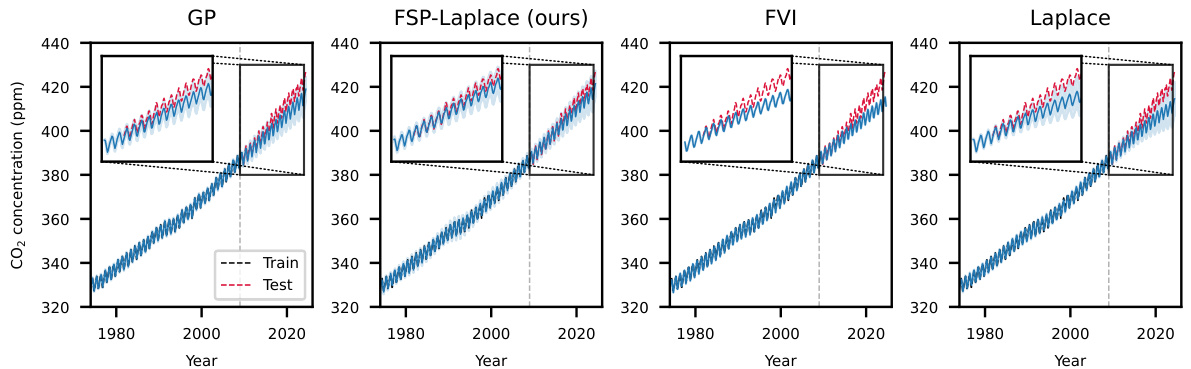
🔼 This table presents a quantitative comparison of the proposed FSP-LAPLACE method against several baselines on two real-world scientific modeling tasks: predicting monthly average atmospheric CO2 concentration at the Mauna Loa Observatory and predicting ocean currents in the Gulf of Mexico. The table shows the expected log-likelihood and mean squared error for each method. The results demonstrate that incorporating prior knowledge via a Gaussian process prior in FSP-LAPLACE leads to improved performance compared to the standard Laplace approximation, highlighting the effectiveness of the proposed approach.
read the caption
Table 1: Results for the Mauna Loa CO2 prediction and ocean current modeling tasks. Incorporating knowledge via the GP prior in our FSP-LAPLACE improves performance over the standard Laplace.

🔼 This table presents the results of the MNIST and FashionMNIST image classification experiments. Several metrics are compared across different models: FSP-LAPLACE (using two different methods for selecting context points), FVI, Laplace, MAP, and Sparse GP. The metrics include test log-likelihood, accuracy, expected calibration error (ECE), and out-of-distribution (OOD) detection accuracy. FSP-LAPLACE demonstrates competitive performance, often outperforming other methods in terms of log-likelihood and OOD accuracy, while maintaining high accuracy and low ECE.
read the caption
Table 2: Test expected log-likelihood, accuracy, expected calibration error and OOD detection accuracy on MNIST and FashionMNIST. FSP-LAPLACE performs strongly among baselines matching the accuracy of best-performing baselines and obtaining the highest expected log-likelihood and out-of-distribution detection accuracy.

🔼 This table presents a quantitative comparison of the FSP-LAPLACE method against several baselines (FVI, Laplace, and GP) on two real-world tasks: Mauna Loa CO2 prediction and ocean current modeling. The results show the expected log-likelihood and mean squared error for each method. The improved performance of FSP-LAPLACE, especially in terms of expected log-likelihood, highlights the benefits of incorporating prior knowledge via Gaussian process priors.
read the caption
Table 1: Results for the Mauna Loa CO2 prediction and ocean current modeling tasks. Incorporating knowledge via the GP prior in our FSP-LAPLACE improves performance over the standard Laplace.

🔼 This table shows the ratio of the Frobenius norm of PAPᵀ to the Frobenius norm of A for different kernel functions (RBF and Matern-1/2) and tasks (regression and classification). This ratio is used to demonstrate that the term ||PAPᵀ||F is negligible compared to ||A||F in the Hessian approximation used in the paper. Small values in this table support the approximation used to improve computational efficiency.
read the caption
Table C.2: ||PAP®||F/||A||F for different combinations of priors and tasks.
Full paper#