Looks Too Good To Be True: An Information-Theoretic Analysis of Hallucinations in Generative Restoration Models

↗ arXiv ↗ Hugging Face

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it reveals a fundamental trade-off between the perceptual quality and reliability of image restoration models. Understanding this limitation is vital for responsible development and deployment of these powerful, yet potentially unreliable, AI systems. This work provides a theoretical framework and empirical evidence to guide informed decision-making in applications where safety is paramount.

Visual Insights

#

🔼 This figure illustrates Theorem 3 of the paper, which describes a fundamental trade-off between uncertainty and perception in image restoration tasks. The x-axis represents the perceptual quality of the restored image, while the y-axis represents the uncertainty associated with the restoration. The red curve shows the lower bound on the attainable uncertainty as a function of perceptual quality. The curve starts at the inherent uncertainty (Uinherent) of the restoration problem and gradually increases to twice this value as the perceptual quality approaches perfection. The shaded red region indicates an impossible region where it’s impossible to achieve both high perceptual quality and low uncertainty simultaneously. The green region shows the possible region of attainable uncertainty and perceptual quality. This trade-off highlights the inherent limitations of generative models in achieving both high perceptual quality and reliable predictions.

read the caption

Figure 1: Illustration of Theorem 3. In restoration tasks, the minimal attainable uncertainty is lower bounded by a function that begins at the inherent uncertainty UInherent of the problem (Definition 2) and gradually increases up to twice this value as the recovery approaches perfect perceptual quality.

In-depth insights

#

Uncertainty-Perception Tradeoff

#

The core concept of the “Uncertainty-Perception Tradeoff” revolves around the inherent limitations of generative models in simultaneously achieving high perceptual quality and reliable predictions. The paper rigorously demonstrates that perfect perceptual quality necessitates at least twice the inherent uncertainty of the restoration problem. This tradeoff is not merely an empirical observation, but a fundamental limitation rooted in information theory, specifically highlighted by the relationship between entropy, and perceptual quality measures like Rényi divergence. The global minimal uncertainty grows proportionally with perception quality, establishing a fundamental limit to how well generative restoration models can perform. This work expands beyond the traditional perception-distortion tradeoff, offering a new perspective on model limitations. It emphasizes that increased perceptual realism frequently accompanies higher uncertainty, which manifests as hallucinations – convincing-looking details that are not present in the original data. This implies that prioritization between perceptual fidelity and prediction reliability needs to be considered carefully by practitioners; prioritizing one will inherently compromise the other.

Generative Model Limits

#

Generative models, while revolutionizing image restoration with impressive perceptual quality, are fundamentally limited by an inherent tradeoff between perceptual quality and uncertainty. The pursuit of perfect perceptual realism necessitates a level of uncertainty at least double the inherent uncertainty of the restoration problem itself. This implies that achieving high perceptual quality inevitably increases the risk of hallucinations and unreliable predictions. The inherent uncertainty is a fundamental limit stemming from the ill-posed nature of inverse problems, where multiple solutions explain the same observations. This tradeoff is mathematically proven and experimentally validated across various models and tasks. Understanding this limitation is crucial for responsible development and deployment of these powerful but inherently uncertain models, particularly in applications demanding high reliability, such as medical imaging. Prioritizing safety over purely perceptual performance is paramount, especially in sensitive contexts.

Rényi Divergence Analysis

#

A Rényi Divergence Analysis section in a research paper would likely explore the use of Rényi divergence as a measure of perceptual quality in image restoration tasks. This choice is motivated by Rényi divergence’s versatility, encompassing various other distance measures like KL divergence and Hellinger distance as special cases. The analysis would likely involve deriving bounds on the minimum uncertainty achievable for a given level of perceptual quality (as measured by Rényi divergence). This would establish a fundamental trade-off between uncertainty and perception, showing that perfect perceptual quality necessitates a minimum level of uncertainty. The analysis might also investigate how this trade-off is affected by the underlying data distributions and model parameters, potentially demonstrating that the trade-off is more severe in higher dimensions. Empirical validation, possibly through experiments with super-resolution and inpainting algorithms, would be crucial in supporting these theoretical findings. The overall contribution would be to provide a deeper understanding of the inherent limitations of generative models in achieving both high perceptual quality and reliable predictions, thereby informing best practices for developing and deploying image restoration models.

Inherent Uncertainty

#

The concept of “Inherent Uncertainty” in generative image restoration models is crucial. It refers to the fundamental limits in perfectly recovering an image from degraded observations due to the ill-posed nature of the inverse problem. This inherent uncertainty is not a flaw of specific algorithms but a property of the restoration task itself. The paper defines it rigorously using information theory, quantifying the irreducible information loss during the degradation process. This is significant because it establishes a fundamental lower bound on achievable uncertainty, irrespective of the restoration method employed. Understanding this inherent uncertainty is key to setting realistic expectations for generative models and appreciating the trade-offs between perception quality and uncertainty quantification. It fundamentally limits how well any algorithm can perform, regardless of sophistication, thus providing context to evaluate algorithm performance against a theoretical optimum rather than just empirical metrics.

High-Dimension Challenges

#

High-dimensionality presents significant hurdles in various aspects of the research. Accurately estimating entropy and other information-theoretic measures in high-dimensional spaces is computationally expensive and prone to error. The ‘curse of dimensionality’ makes accurate density estimation challenging, necessitating the use of alternative methods or approximations. This limitation impacts the reliability of uncertainty quantification, influencing the precision and generalizability of the uncertainty-perception tradeoff analysis. Practical solutions require careful consideration, potentially employing dimensionality reduction techniques, alternative statistical estimators, or focusing on specific aspects of high-dimensional distributions. Despite these challenges, the paper’s theoretical framework offers valuable insights even with its high-dimensional limitations. Further research should focus on addressing these computational challenges to improve the accuracy and efficiency of applying the proposed framework in practical, high-dimensional settings.

More visual insights

#

More on figures

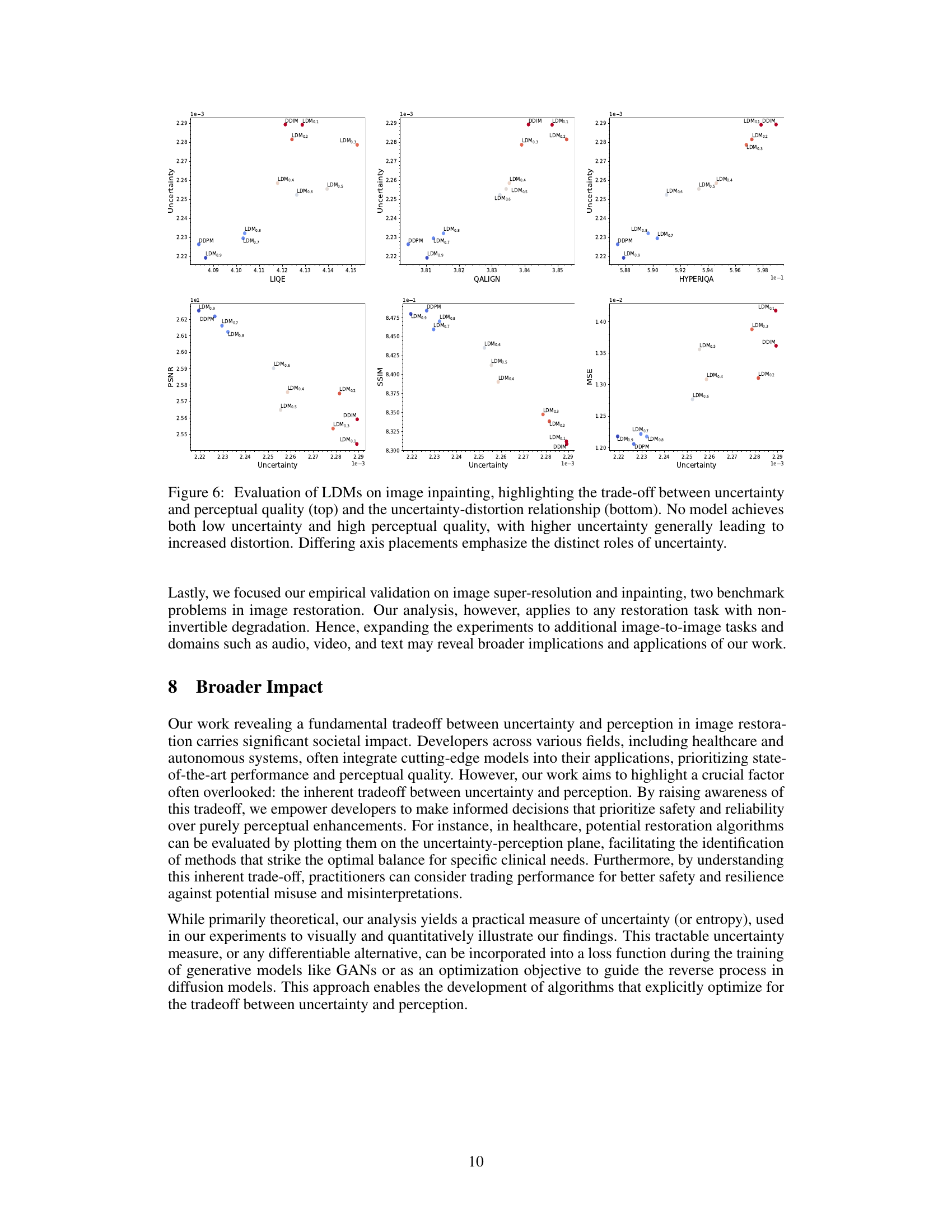
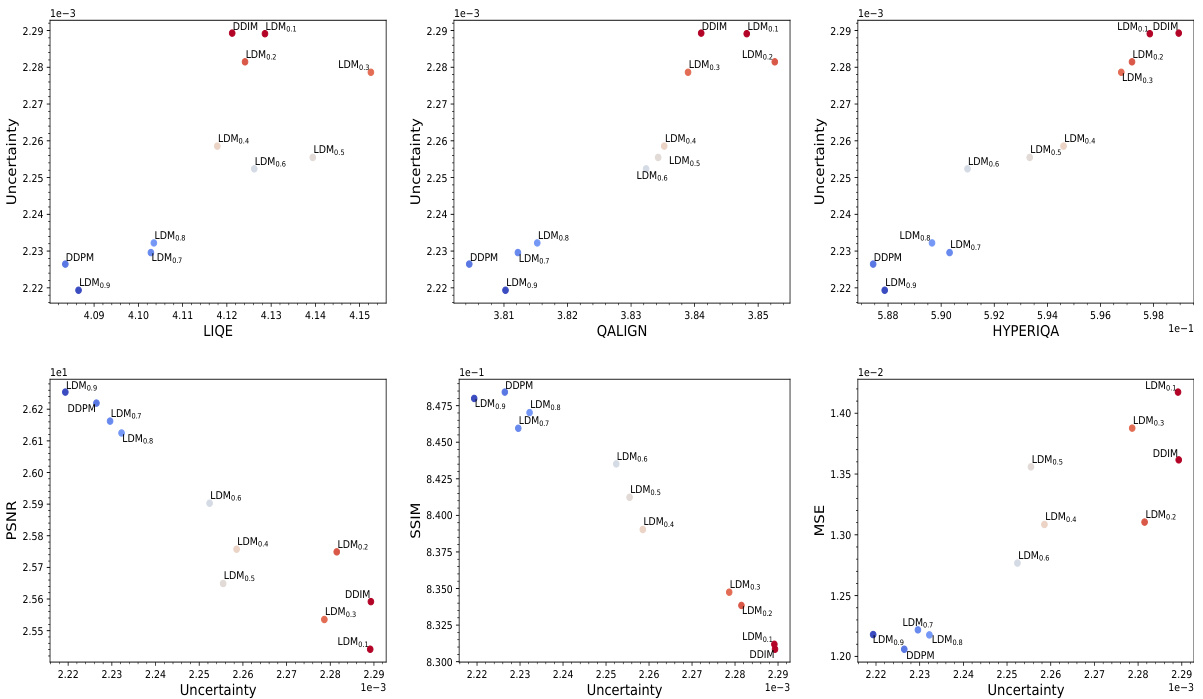
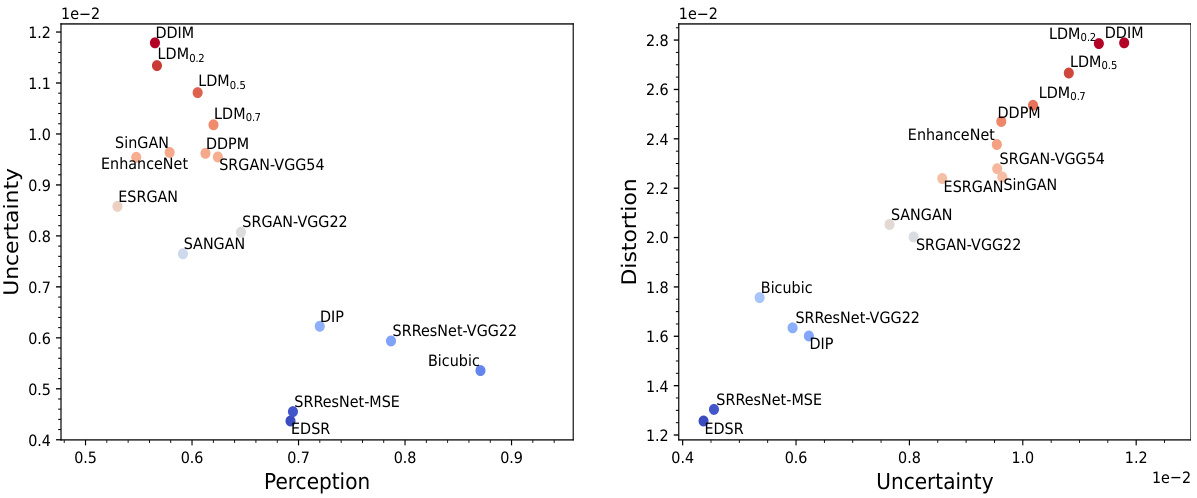
🔼 This figure shows the results of image inpainting using different algorithms. The algorithms are ordered from left to right, with each subsequent algorithm producing higher perceptual quality. However, as the perceptual quality improves, so does the level of uncertainty (hallucinations) and distortion in the generated images. The reference image is on the far left, followed by the measurements(input) and then results from three different algorithms. This illustrates the tradeoff between achieving high perceptual quality and the risk of generating unrealistic details (hallucinations) that were not present in the original image.

read the caption

Figure 2: Image inpainting results. Algorithms are ordered from low to high perception (left to right). Note the corresponding increased hallucinations and distortion. See Section 5 for details.

🔼 This figure illustrates the uncertainty-perception tradeoff. The x-axis represents the Rényi divergence of order 1/2 (a measure of perceptual quality), and the y-axis represents the entropy power of the error (a measure of uncertainty). The plane is divided into three regions: impossible (red), optimal (green), and suboptimal (light blue). The impossible region shows the inherent limit: perfect perception requires at least twice the inherent uncertainty. The optimal region shows the best possible uncertainty for a given level of perception, while the suboptimal region shows estimators with higher-than-necessary uncertainty. This visualization helps practitioners understand and balance the trade-off between these two factors.

read the caption

Figure 3: The uncertainty-perception plane (Theorem 3). The impossible region demonstrates the inherent tradeoff between perception and uncertainty, while other regions may guide practitioners toward estimators that better balance the two factors, highlighting potential areas for improvement.

🔼 This figure shows how the uncertainty-perception tradeoff changes with the dimensionality (d) of the data. As dimensionality increases, the tradeoff becomes more severe. In other words, even small improvements in perceptual quality require a much larger increase in uncertainty in higher dimensions. The curves show the function η(P;d) for various dimensions d, which relates the minimal uncertainty to the perceptual quality.

read the caption

Figure 4: Impact of dimensionality, as revealed in Theorem 3, demonstrates that the uncertainty-perception tradeoff intensifies in higher dimensions. This implies that even minor improvements in perceptual quality for an algorithm may come at the cost of a significant increase in uncertainty.

🔼 This figure illustrates the uncertainty-perception tradeoff, a core concept of the paper. The x-axis represents the perceptual quality (measured by Rényi divergence), and the y-axis represents the uncertainty (measured by entropy power). The plot shows three distinct regions: an ‘impossible’ region where no estimator can simultaneously achieve both high perceptual quality and low uncertainty, an ‘optimal’ region where estimators balance these two factors, and a ‘suboptimal’ region where estimators have high uncertainty despite decent perceptual quality. This visually represents the fundamental tradeoff between perceptual quality and uncertainty in image restoration, guiding practitioners to make informed decisions when prioritizing one over the other.

read the caption

Figure 3: The uncertainty-perception plane (Theorem 3). The impossible region demonstrates the inherent tradeoff between perception and uncertainty, while other regions may guide practitioners toward estimators that better balance the two factors, highlighting potential areas for improvement.

🔼 This figure illustrates the uncertainty-perception tradeoff described in Theorem 3 of the paper. It shows a plot with uncertainty on the y-axis and perception on the x-axis. The plot is divided into three regions: an impossible region representing combinations of high perception and low uncertainty that are unattainable; an optimal region where estimators achieve a good balance between perception and uncertainty; and a suboptimal region where estimators have high uncertainty and lower perception. The figure highlights the inherent tradeoff between these two factors, guiding practitioners to make informed choices when deploying generative models.

read the caption

Figure 3: The uncertainty-perception plane (Theorem 3). The impossible region demonstrates the inherent tradeoff between perception and uncertainty, while other regions may guide practitioners toward estimators that better balance the two factors, highlighting potential areas for improvement.

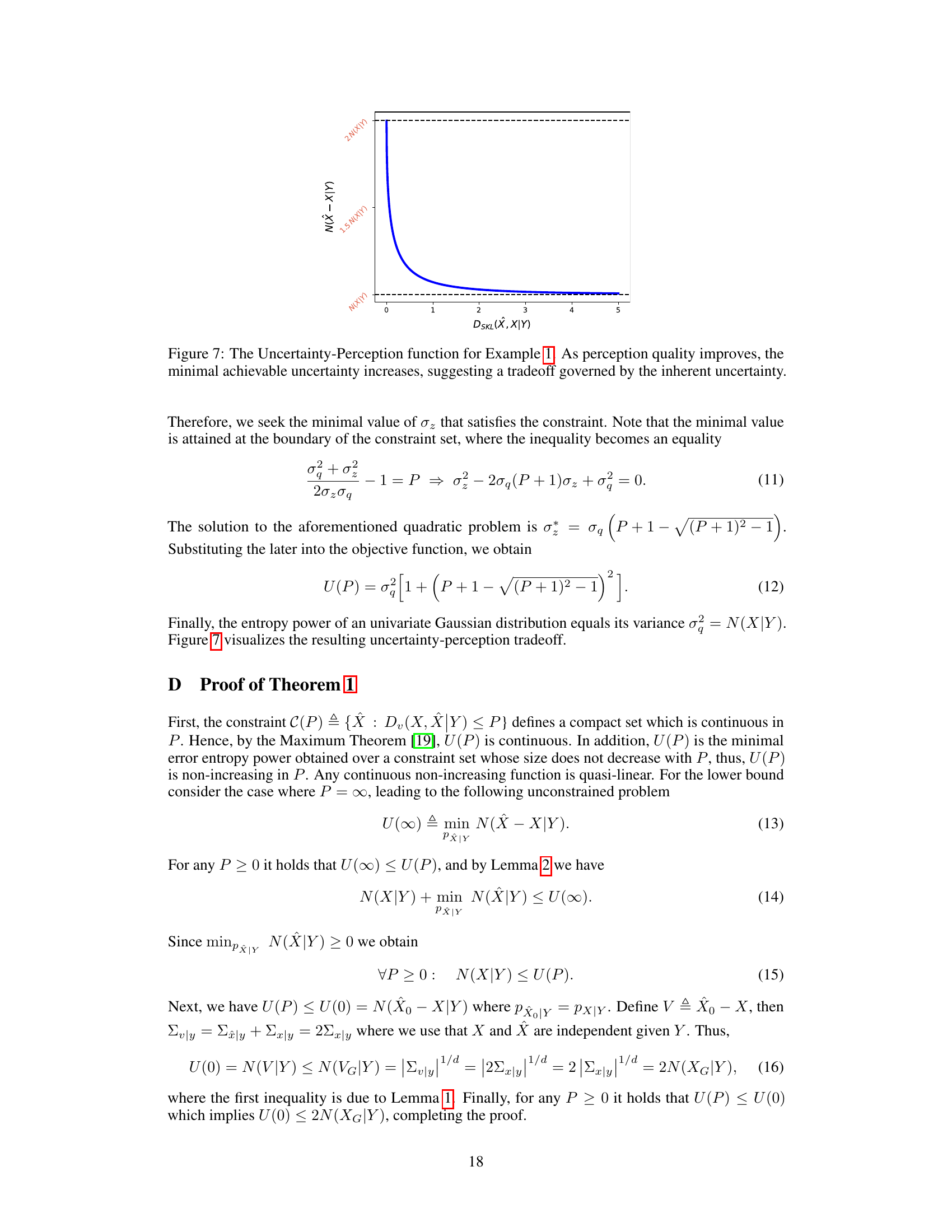
🔼 This figure illustrates the relationship between uncertainty and perception quality in the context of a simple example (Example 1) discussed in the paper. The x-axis represents the perception quality, measured by the symmetric Kullback-Leibler (KL) divergence. The y-axis shows the minimal achievable uncertainty, represented by the entropy power of the error. The curve shows that as perception quality increases (divergence decreases towards 0), the uncertainty also increases, approaching a limit of twice the inherent uncertainty. This demonstrates the fundamental tradeoff between these two factors.

read the caption

Figure 7: The Uncertainty-Perception function for Example 1. As perception quality improves, the minimal achievable uncertainty increases, suggesting a tradeoff governed by the inherent uncertainty.

🔼 This figure illustrates the uncertainty-perception tradeoff. The x-axis represents the perceptual quality (D1/2(X, X|Y)), and the y-axis represents the uncertainty (N(X-X|Y)). The plane is divided into three regions: 1. Impossible Region: No estimator can achieve both low uncertainty and high perceptual quality simultaneously. This highlights the fundamental tradeoff. 2. Optimal Region: Estimators that achieve the minimum attainable uncertainty for a given perceptual quality. 3. Suboptimal Region: Estimators that exhibit higher uncertainty than is minimally necessary for their perceptual quality. This suggests there is room for improvement in these algorithms. The figure shows that as perceptual quality improves, uncertainty increases. The impossible region emphasizes this inherent tradeoff, illustrating a key finding of the paper.

read the caption

Figure 3: The uncertainty-perception plane (Theorem 3). The impossible region demonstrates the inherent tradeoff between perception and uncertainty, while other regions may guide practitioners toward estimators that better balance the two factors, highlighting potential areas for improvement.

Full paper

#