TL;DR#
Current unsupervised representation learning methods struggle with tasks requiring precise features due to their reliance on transformation-invariant representations. While equivariant representation learning addresses this by capturing transformation-sensitive information, existing approaches depend on transformation labels, limiting their scalability and applicability to complex transformations. This often leads to a performance degradation.
The proposed Self-Supervised Transformation Learning (STL) method addresses these issues by replacing transformation labels with transformation representations derived from image pairs. This approach learns image-invariant transformation representations while ensuring that learned equivariant transformations are image-invariant. STL demonstrates improved performance across diverse classification and detection tasks, exceeding existing methods in several benchmarks. The integration of complex transformations, previously unusable by other equivariant methods, further showcases STL’s flexibility and robustness.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel self-supervised approach to equivariant representation learning, overcoming limitations of existing methods that rely on transformation labels. This advance is significant for computer vision tasks requiring precise feature extraction, such as object localization and fine-grained classification, and opens up new avenues for research into more complex and adaptable equivariant models.
Visual Insights#
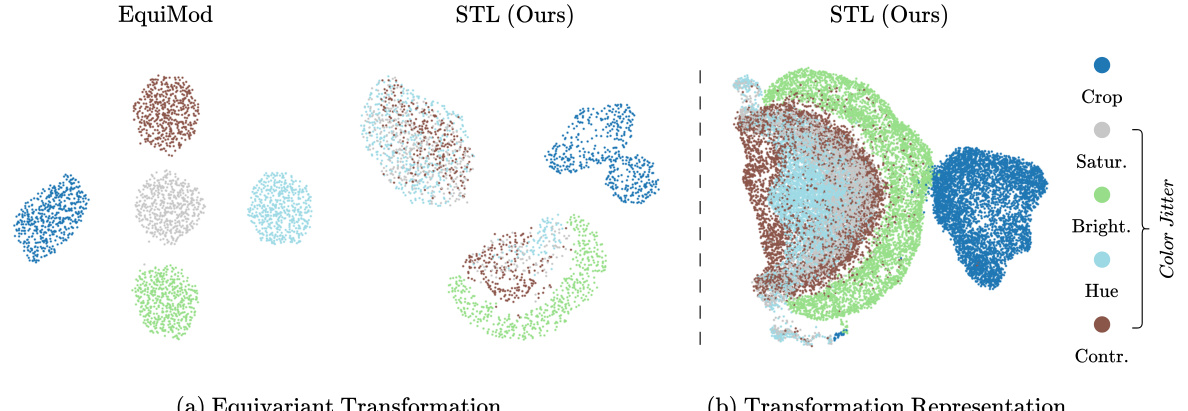
🔼 This figure visualizes the difference between EquiMod and STL in generating equivariant transformations and transformation representations. UMAP plots show that EquiMod uses transformation labels to generate functional weights for its equivariant transformations, resulting in separate clusters for each transformation type. In contrast, STL derives its transformation representations from image pairs, resulting in clusters that group similar transformations together, regardless of their individual labels. This highlights STL’s ability to learn the relationships between different transformations, even without explicit labels.
read the caption
Figure 1: Visualization of Equivariant Transformation and Transformation Representation. (Left) UMAP [32] visualizations of functional weights from equivariant transformations implemented with a hypernetwork. EquiMod uses transformation labels to generate these weights, while STL derives them from the representation pairs of transformed and original image. (Right) UMAP visualizations of transformation representations obtained from representation pairs of original input image and transformed input image.
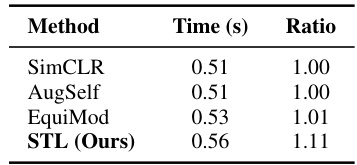
🔼 This table shows the computational cost (forward and backward pass time per iteration) for different methods, including SimCLR, AugSelf, EquiMod, and STL. The experiments were conducted on an NVIDIA 3090 GPU using ResNet-50 and a batch size of 256. The ‘Ratio’ column normalizes the time taken by each method relative to SimCLR, providing a direct comparison of their computational efficiency.
read the caption
Table 1: Computational Cost. Forward-backward time per iteration on NVIDIA 3090 GPU with ResNet-50 and batch size 256.
In-depth insights#
STL: Core Idea#
The core idea of Self-supervised Transformation Learning (STL) is to replace explicit transformation labels in equivariant learning with self-supervised transformation representations. Instead of relying on predefined labels, STL learns a representation of the transformation itself from pairs of image representations: one original and one transformed. This transformation representation is designed to be invariant to the specific input image but sensitive to the type of transformation applied. The key innovation is the use of contrastive learning to ensure this invariance, aligning transformation representations from different image pairs that underwent the same transformation. This eliminates the limitations of existing methods which depend on transformation labels that struggle with interdependency and complex transformations. STL’s ability to handle complex transformations and leverage unsupervised learning makes it more adaptable and robust, while maintaining comparable computational efficiency.
Equivariant Learning#
Equivariant learning is a crucial concept in machine learning that focuses on creating representations which transform in a predictable way when the input data undergoes a transformation. Unlike invariant learning, which aims for representations unaffected by transformations, equivariant learning acknowledges and leverages the transformation’s effect. This approach is particularly valuable for tasks like object detection or pose estimation, where the spatial relationships within the data are critical. Self-supervised approaches are increasingly important to equivariant learning as they avoid the need for labeled transformation data, thereby making the approach more versatile and broadly applicable. By using techniques such as contrastive learning with transformation representation, algorithms can learn to capture the nuanced relationship between input and output transformations. The challenge lies in designing models that are both equivariant and robust, capable of handling complex transformations without excessive computational costs. The integration of advanced methods like AugMix, capable of handling highly complex augmentations, also presents promising avenues for enhancement. Future research could focus on scaling equivariant methods to handle more complex data and transformations.
Transform. Rep.#
The heading ‘Transform. Rep.’ likely refers to transformation representations, a core concept in the paper. It suggests the paper explores methods to represent transformations (e.g., image augmentations like cropping or color jittering) not as labels, but as data itself within a learned embedding space. This is crucial because using transformation representations, instead of explicit labels, allows the model to learn richer, more nuanced relationships between transformations. The key advantage is likely the ability to handle complex or sequential transformations, which would be difficult to represent with discrete labels. The paper probably demonstrates how this approach improves the learning of equivariant representations, which are representations that change predictably in response to transformations, achieving better performance on downstream tasks like image classification and object detection. Self-supervised learning is likely leveraged to learn these representations, implying the paper contrasts transformed and original image representations without explicit supervision. The effectiveness of this approach hinges on the quality of the learned transformation representations, potentially evaluated through metrics such as transformation prediction accuracy or clustering of similar transformations in the embedding space. Ultimately, this section likely provides the core technical contribution of the paper, showcasing a novel and effective approach to representation learning.
Ablation Study#
An ablation study systematically removes components of a model to assess their individual contributions. In the context of a machine learning paper, this involves isolating the impact of specific design choices—like a particular loss function, a specific module, or a data augmentation technique—by training a modified version of the model without that element. By comparing the performance of the complete model to those of the simplified versions, researchers can quantify the importance of each component in achieving the overall results. This method helps establish causality, showing if a given component is essential to success or if it only contributes marginally. Moreover, ablation studies offer valuable insights into the model’s inner workings, allowing researchers to identify strengths and weaknesses and to potentially guide future improvements by focusing on the most impactful components. A well-designed ablation study is crucial for demonstrating the effectiveness of a novel method, clarifying the importance of various design decisions, and validating its contribution to the field.
Future Work#
The paper’s omission of a dedicated “Future Work” section presents an opportunity for expansion. Extending the STL framework to handle more complex transformations beyond single image pairs, such as those involving multiple images or intricate sequences, is crucial. This would involve developing methods to represent and effectively utilize the information inherent in these complex transformations. Investigating the application of STL to other modalities beyond computer vision, like audio or natural language processing, could broaden its impact. A deeper exploration of the relationship between the complexity of transformations and performance is needed, potentially identifying thresholds or optimal complexity levels. Finally, a detailed analysis of STL’s generalization capabilities in diverse scenarios and its resilience to noisy or adversarial inputs should be pursued to strengthen its real-world applicability. The current evaluation provides a strong foundation, but further testing with varied datasets and downstream tasks is needed to verify the robustness and generalizability of the proposed method.
More visual insights#
More on figures
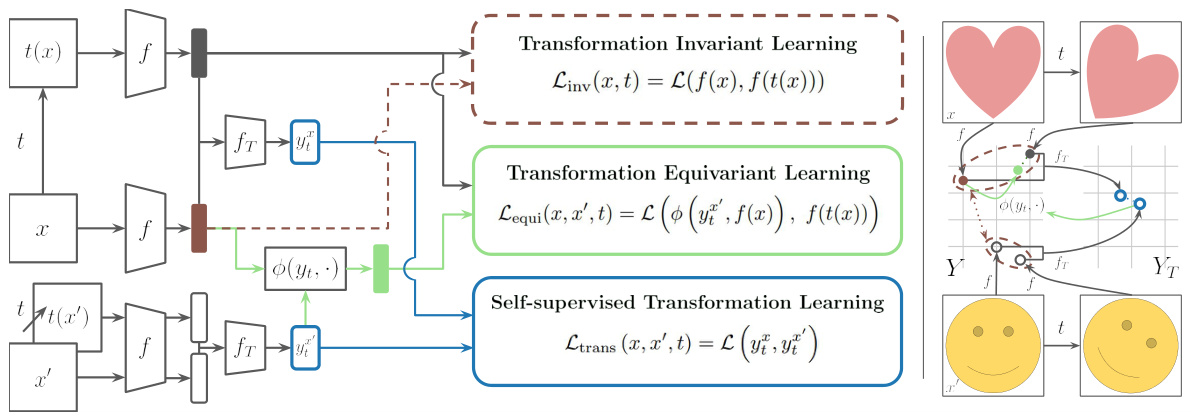
🔼 This figure illustrates the framework of Self-Supervised Transformation Learning (STL). The left panel shows the overall architecture, highlighting the three main learning objectives: transformation invariant learning (aligning representations of original and transformed images), transformation equivariant learning (aligning transformed image representations with equivariant transformations derived from transformation representations of different images), and self-supervised transformation learning (aligning transformation representations from different image pairs). The right panel visually depicts the transformations applied to images and their representations, and how the equivariant transformations are learned in the representation space.
read the caption
Figure 2: Transformation Equivariant Learning with Self-supervised Transformation Learning. (Left) The overall framework of STL. For given image and transformations, it demonstrates: 1) transformation invariant learning, which aligns the representations of image and transformed image; 2) transformation equivariant learning, where the representation of image transformed by an equivariant transformation (obtained from the transformation representation of different image with the same applied transformation) aligns with the transformed image's representation; 3) self-supervised transformation learning, which aligns the transformation representations obtained from different image pairs. (Right) It illustrates the transformations of each representation and the equivariant transformations within the representation space.

🔼 This figure illustrates the difference in batch composition between standard self-supervised learning methods and the proposed STL method. In standard methods (left), each image receives two different transformations. STL (right) pairs images together and applies the same transformation pair to both, enabling the learning of transformation representations.
read the caption
Figure 3: Aligned Transformed Batch. (Left) In self-supervised learning methods, batch compositions typically involve applying two different transformations to each input image. (Right) In STL, batches are composed by pairing two images together, and applying the same transformation pair.

🔼 This figure shows UMAP visualizations of transformation representations. Each point represents a transformation representation, colored and positioned according to the transformation type and intensity level. The visualization reveals how STL learns to represent transformations, clustering similar transformations together and showing the relationship between intensity and representation.
read the caption
Figure 4: Visualization of Transformation Representations by Intensity. UMAP visualization of transformation representations organized by intensity levels for each transformation type, including random crop and color jitter variations in brightness, contrast, saturation, and hue. Parameter ranges for each transformation are divided into four segments to apply varying intensities. Representations are captured by a ResNet-18 model pretrained on STL10 with a transformation backbone.

🔼 This figure illustrates the difference between explicit and implicit equivariant learning methods. Explicit methods, such as SEN, EquiMod, and SIE, use a dedicated transformation network operating directly on representations, requiring explicit transformation labels for alignment. In contrast, implicit methods, like E-SSL and AugSelf, infer transformations indirectly without explicit transformation labels; they leverage auxiliary tasks to deduce transformation states based on changes in the representations.
read the caption
Figure 5: Explicit and Implicit Equivariant Learning. Transformation equivariant learning with transformations is divided into (Left) explicit and (Right) implicit equivariant learning.
More on tables
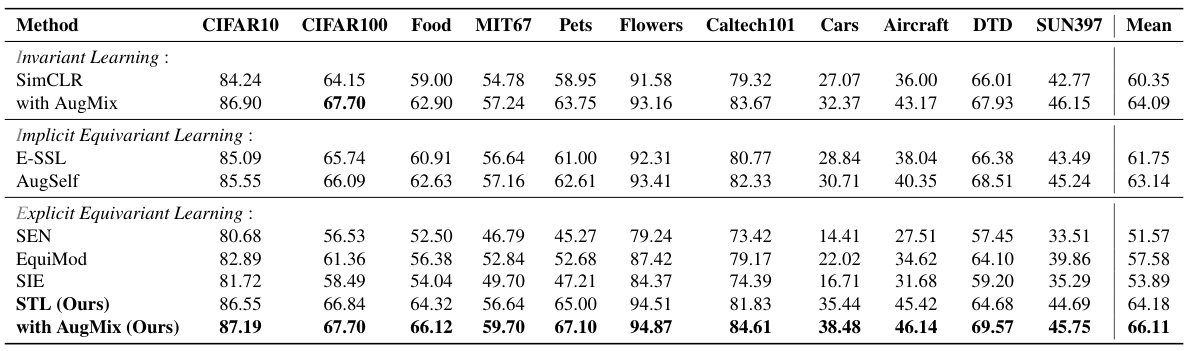
🔼 This table presents the results of evaluating the generalizability of learned representations on various downstream classification tasks. It compares different representation learning methods (invariant, implicit equivariant, explicit equivariant, and STL) by measuring their linear evaluation accuracy on 11 different datasets (CIFAR10, CIFAR100, Food101, MIT67, Pets, Flowers, Caltech101, Cars, Aircraft, DTD, SUN397). The ResNet-50 model was pretrained on ImageNet100 for all methods. The results show STL’s superior performance across many datasets, demonstrating robust generalization.
read the caption
Table 2: Out-domain Classification. Evaluation of representation generalizability on the out-domain downstream classification tasks. Linear evaluation accuracy (%) is reported for ResNet-50 pretrained on ImageNet100.
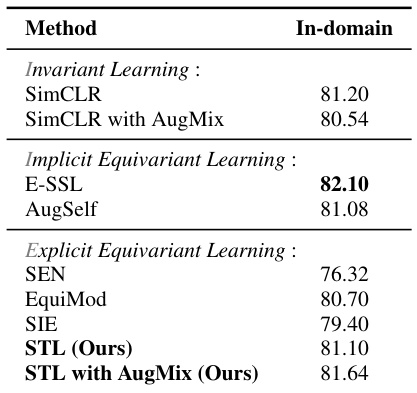
🔼 This table presents the linear evaluation accuracy of ResNet-50, pretrained on ImageNet100, for an in-domain classification task. It compares the performance of various methods including invariant learning (SimCLR, SimCLR with AugMix), implicit equivariant learning (E-SSL, AugSelf), and explicit equivariant learning (SEN, EquiMod, SIE) against the proposed method, STL, with and without AugMix. The results show the in-domain classification accuracy for each method, allowing for a direct comparison of their performance on this specific task.
read the caption
Table 3: In-domain Classification. Evaluation of representation on in-domain classification task. Linear evaluation accuracy (%) is reported for ResNet-50 pretrained on ImageNet100.
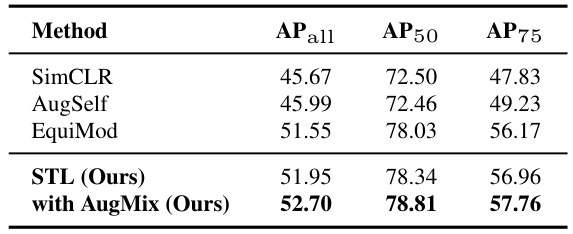
🔼 This table presents the results of an object detection experiment on the VOC07+12 dataset. The model used is a ResNet-50, pre-trained on ImageNet100, and fine-tuned for object detection. Different methods are compared, including SimCLR (invariant learning), AugSelf (implicit equivariant learning), EquiMod (explicit equivariant learning), and STL (the authors’ proposed self-supervised transformation learning method), both with and without AugMix. The metrics used are AP (Average Precision), AP50 (Average Precision at IoU threshold of 0.5), and AP75 (Average Precision at IoU threshold of 0.75). The table demonstrates the performance improvements achieved by STL, especially when combined with AugMix.
read the caption
Table 4: Object Detection. Evaluation of representation generalizability on a downstream object detection task. Average precision is reported for ImageNet100-pretrained ResNet-50 fine-tuned on VOC07+12.
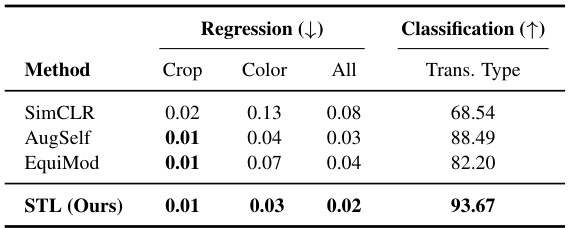
🔼 This table presents the results of evaluating the quality of transformation representations learned by different methods. The evaluation is done using two tasks: regression (measuring the difference between the predicted and actual transformation parameters using Mean Squared Error) and classification (measuring the accuracy of predicting the type of transformation applied). The table shows that STL (Self-supervised Transformation Learning) achieves significantly better performance than the other methods in both tasks, indicating that STL learns more accurate and informative transformation representations.
read the caption
Table 5: Transformation Prediction. Evaluation of transformation representation from learned representation pairs. Regression tasks use MSE loss, and transformation type classification uses accuracy.

🔼 This table presents the performance of the proposed STL model’s equivariant transformation. It compares the Mean Reciprocal Rank (MRR), Hit@1, Hit@5, and Precision (PRE) metrics for crop and color jitter transformations, separately and combined. The results are compared against three existing equivariant learning methods (SEN, EquiMod, and SIE) and an ablation study where the transformation learning loss (Ltrans) is removed from the STL model. Higher MRR and H@k indicate better equivariance, while a lower PRE value indicates higher precision in predicting the transformations’ parameter vector.
read the caption
Table 6: Transformation Equivariance. Evaluation of the equivariant transformation. Mean Reciprocal Rank (MRR), Hit@k (H@k), and Precision (PRE) metrics on various transformations (crop and color jitter).
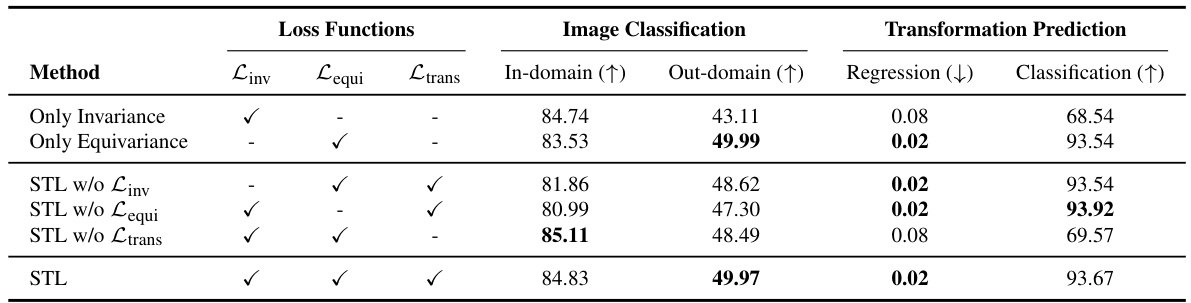
🔼 This table presents the ablation study of the three loss functions used in STL: Linv (invariant learning), Lequi (equivariant learning), and Ltrans (self-supervised transformation learning). It shows the impact of each loss function on both image classification (in-domain and out-domain accuracy) and transformation prediction (regression and classification accuracy) using ResNet-18 model pretrained on STL10 dataset. The results highlight the contribution of each loss function to the overall performance.
read the caption
Table 7: Loss Function Ablation Study. Image classification and transformation prediction results of ResNet-18 pretrained on STL10 with selective inclusion of loss terms for invariant learning (Linv), equivariant learning (Lequi), and self-supervised transformation learning (Ltrans). For image classification, in-domain accuracy (%) and the average accuracy (%) across multiple out-domain datasets are shown. For transformation prediction, MSE is used for regression of crop and color transformations, and accuracy (%) is used for transformation type classification.
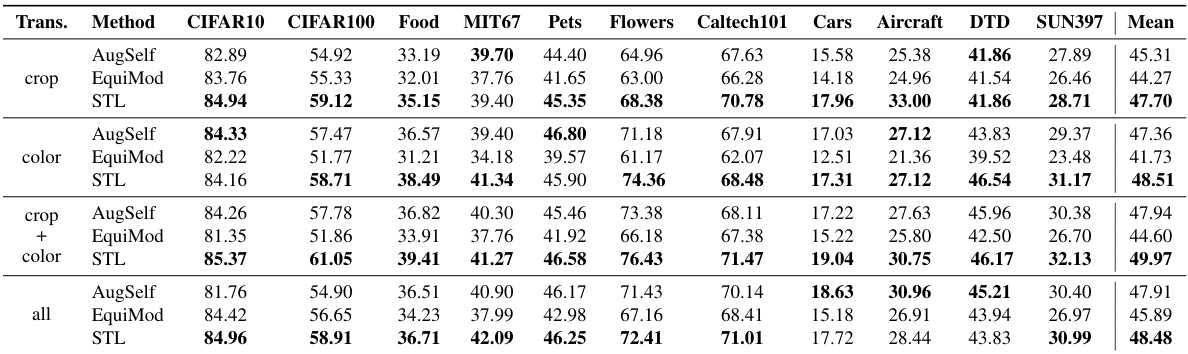
🔼 This table presents the results of an ablation study investigating the impact of different transformations (crop, color, and a combination of both) on the performance of the STL model. It shows linear evaluation accuracy on various downstream classification tasks (CIFAR10, CIFAR100, Food, MIT67, Pets, Flowers, Caltech101, Cars, Aircraft, DTD, SUN397). The results are broken down for AugSelf, EquiMod, and the proposed STL method to compare their performance under different transformation settings.
read the caption
Table 8: Transformation Ablation Study. Linear evaluation accuracy (%) of ResNet-18 pretrained on STL10 with various transformations used as equivariance targets.

🔼 This table presents the results of an ablation study that investigates the impact of different base invariant learning models on the performance of the proposed Self-Supervised Transformation Learning (STL) method. The study uses linear evaluation accuracy as the metric across eleven downstream classification tasks (including CIFAR-10, CIFAR-100, Food-101, etc.) to compare STL’s performance when integrated with various base models like SimCLR, BYOL, SimSiam, and Barlow Twins. The results demonstrate STL’s flexibility and adaptability by showing consistent improvements in performance across different base models, highlighting its broad applicability.
read the caption
Table 9: Base Invariant Learning Model Ablation Study. Linear evaluation accuracy (%) of ResNet-18 pretrained on STL10 with various base models for invariant learning.

🔼 This table presents the linear evaluation accuracy of ResNet-50, pretrained on ImageNet100, across eleven different downstream classification tasks. The results are broken down by method (invariant learning techniques like SimCLR, implicit equivariant methods like E-SSL and AugSelf, explicit equivariant methods like SEN, EquiMod, and SIE, and the proposed STL method, both with and without AugMix augmentation). The accuracy for each method is shown for each dataset (CIFAR-10, CIFAR-100, Food-101, MIT67, Pets, Flowers, Caltech-101, Cars, Aircraft, DTD, and SUN397). This allows for a comparison of the different methods’ ability to generalize to unseen datasets.
read the caption
Table 2: Out-domain Classification. Evaluation of representation generalizability on the out-domain downstream classification tasks. Linear evaluation accuracy (%) is reported for ResNet-50 pretrained on ImageNet100.
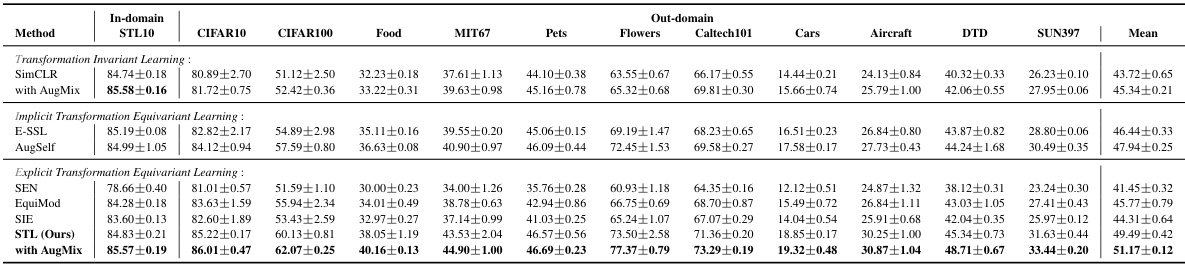
🔼 This table presents the results of evaluating the generalizability of learned representations on various out-of-domain datasets. It compares different representation learning methods (invariant, implicit equivariant, explicit equivariant, and the proposed STL method) by measuring their linear evaluation accuracy on 11 diverse downstream classification tasks using a ResNet-50 model pre-trained on ImageNet100. The table showcases the performance of each method with and without AugMix augmentation, highlighting the robustness of the different approaches.
read the caption
Table 2: Out-domain Classification. Evaluation of representation generalizability on the out-domain downstream classification tasks. Linear evaluation accuracy (%) is reported for ResNet-50 pretrained on ImageNet100.
Full paper#



















