TL;DR#
Evaluating large language models (LLMs) is challenging due to the high cost and time involved in human evaluation. Prediction-Powered Inference (PPI) methods address this by leveraging automated evaluations, but these are often biased. Previous PPI methods also lack the ability to handle data heterogeneity.
This paper introduces Stratified Prediction-Powered Inference (StratPPI), a method which addresses these challenges by using simple data stratification strategies to compute provably valid confidence intervals. The authors show both theoretically and empirically that StratPPI provides substantially tighter confidence intervals than unstratified approaches, particularly when the quality of automatic labeling varies across different data subsets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in machine learning and NLP because it offers a novel and statistically rigorous method for evaluating language models, especially valuable when human annotation is limited. The improved accuracy and efficiency in evaluation will accelerate progress in LLM development and deployment. StratPPI’s applicability to various domains beyond language models opens exciting avenues for future work.
Visual Insights#

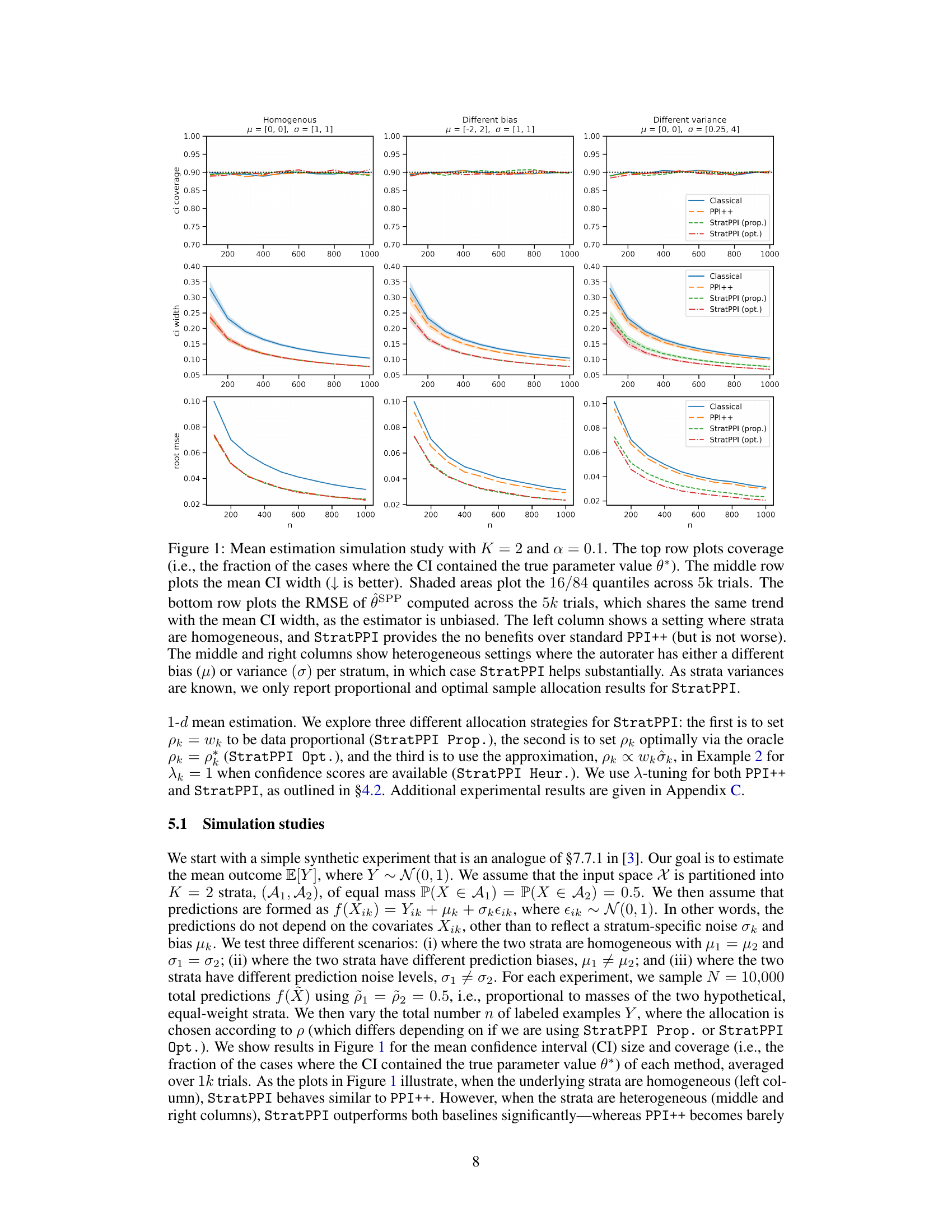
🔼 This figure displays the results of a simulation study comparing different methods for mean estimation. Three scenarios are shown: homogeneous strata, strata with different autorater bias, and strata with different autorater variance. The figure shows the coverage, width, and root mean squared error (RMSE) of confidence intervals (CIs) generated by four different methods: Classical inference, PPI++, StratPPI with proportional allocation, and StratPPI with optimal allocation. The results demonstrate that StratPPI significantly outperforms the other methods in heterogeneous settings (i.e., different bias or variance across strata).
read the caption
Figure 1: Mean estimation simulation study with K = 2 and α = 0.1. The top row plots coverage (i.e., the fraction of the cases where the CI contained the true parameter value θ*). The middle row plots the mean CI width (↓ is better). Shaded areas plot the 16/84 quantiles across 5k trials. The bottom row plots the RMSE of θSPP computed across the 5k trials, which shares the same trend with the mean CI width, as the estimator is unbiased. The left column shows a setting where strata are homogeneous, and StratPPI provides no benefits over standard PPI++ (but is not worse). The middle and right columns show heterogeneous settings where the autorater has either a different bias (μ) or variance (σ) per stratum, in which case StratPPI helps substantially. As strata variances are known, we only report proportional and optimal sample allocation results for StratPPI.
In-depth insights#
StratPPI: Core Idea#
StratPPI enhances prediction-powered inference (PPI) by incorporating stratification, a technique that divides data into homogeneous subgroups based on relevant characteristics. This addresses PPI’s limitation of assuming a uniform relationship between human and automatic labels. By stratifying, StratPPI acknowledges that the accuracy of the automatic labeler (autorater) might vary across different data subgroups, leading to more precise bias estimations. This improved bias correction, coupled with stratum-specific tuning parameters, results in substantially tighter confidence intervals for model performance estimates compared to unstratified PPI. The core strength lies in its ability to leverage the heterogeneity in the data, thereby gaining efficiency and improving the reliability of statistical estimates, particularly when the autorater’s performance varies across different conditional distributions of the data. Optimal allocation of samples across strata further refines the approach, minimizing variance and maximizing the impact of the limited human-labeled data.
Stratified Sampling#
Stratified sampling, a crucial technique in statistics, is thoughtfully employed in this research to enhance the precision of prediction-powered inference (PPI). Instead of treating the entire dataset uniformly, stratification divides it into meaningful subgroups (strata) based on characteristics relevant to the model’s performance or the autorater’s behavior. This targeted approach is particularly valuable when the performance of the model or autorater varies significantly across different subgroups. By stratifying the data, the researchers gain a more nuanced understanding of the underlying relationships and obtain more accurate estimates. The optimal allocation of samples across strata is also addressed, balancing the need for sufficient representation from each group against the overall sample size limitations. This methodology demonstrably leads to improved confidence intervals—smaller and more reliable ranges that better reflect the true parameter values being estimated, leading to a more precise and informative model evaluation. The strategic use of stratified sampling thus addresses critical challenges associated with limited labeled data and varying autorater accuracy, showcasing its importance in reliably evaluating complex machine learning models.
Real Data Results#
A dedicated ‘Real Data Results’ section would ideally present empirical findings on real-world datasets, complementing simulation studies. It should detail the datasets used, describing their characteristics and relevance to the problem. The section would then compare the proposed stratified prediction-powered inference (StratPPI) method against baselines (e.g., classical inference, standard PPI) across multiple metrics. Key metrics would include confidence interval width, coverage probability, and root mean squared error, demonstrating the practical advantages of StratPPI in terms of reduced variance and tighter confidence intervals. Crucially, the results should explore different stratification strategies, perhaps based on autorater confidence or data heterogeneity, to demonstrate how these choices influence performance. Analysis should delve into the reasons behind StratPPI’s success or failure on specific datasets, addressing whether the method’s assumptions hold or whether specific characteristics of the data cause deviations. A discussion of potential limitations in applying StratPPI to real-world scenarios would add valuable context, emphasizing the importance of carefully selecting datasets and stratification techniques.
Limitations#
A thoughtful analysis of the ‘Limitations’ section in a research paper would go beyond a mere listing of shortcomings. It should delve into the methodological choices that introduced constraints, exploring the trade-offs made between feasibility and rigor. A strong analysis would assess the generalizability of findings, considering whether results hold across different datasets, populations, or contexts. It would evaluate the impact of assumptions, explicitly identifying those made and analyzing potential biases resulting from their violation. Scope limitations should be addressed, acknowledging any boundaries in the study’s focus that restrict the breadth of conclusions. Finally, the discussion should propose avenues for future work, highlighting areas where limitations can be addressed and improved upon in future studies. Crucially, this assessment should be done in a way that doesn’t undermine the paper’s value, but rather contributes to a clearer understanding of its contributions and their boundaries.
Future Work#
The paper’s core contribution is a novel stratified prediction-powered inference (StratPPI) method for language model evaluation. Future work could explore several promising avenues. Firstly, extending StratPPI to more complex loss functions beyond mean estimation, such as those used in ranking or other machine learning tasks, would broaden its applicability and impact. Secondly, a more rigorous theoretical analysis of StratPPI’s finite-sample properties is needed to complement the asymptotic results. Thirdly, developing adaptive stratification strategies that automatically determine optimal stratum boundaries based on data characteristics would enhance the method’s practicality and performance, removing the need for pre-defined stratifications. Finally, investigating the impact of poorly calibrated autoraters and exploring methods to improve calibration or mitigate bias would enhance robustness. These directions will further enhance StratPPI’s power and reliability in various settings.
More visual insights#
More on figures

🔼 This figure presents the results of a simulation study comparing different methods for mean estimation. Three different scenarios are considered: homogeneous strata, strata with different bias, and strata with different variance. The figure shows the coverage, width, and RMSE of confidence intervals for each method. The results demonstrate that the stratified prediction-powered inference (StratPPI) method outperforms other methods, particularly in heterogeneous settings.
read the caption
Figure 1: Mean estimation simulation study with K = 2 and α = 0.1. The top row plots coverage (i.e., the fraction of the cases where the CI contained the true parameter value θ*). The middle row plots the mean CI width (↓ is better). Shaded areas plot the 16/84 quantiles across 5k trials. The bottom row plots the RMSE of θ^SPP computed across the 5k trials, which shares the same trend with the mean CI width, as the estimator is unbiased. The left column shows a setting where strata are homogeneous, and StratPPI provides no benefits over standard PPI++ (but is not worse). The middle and right columns show heterogeneous settings where the autorater has either a different bias (μ) or variance (σ) per stratum, in which case StratPPI helps substantially. As strata variances are known, we only report proportional and optimal sample allocation results for StratPPI.

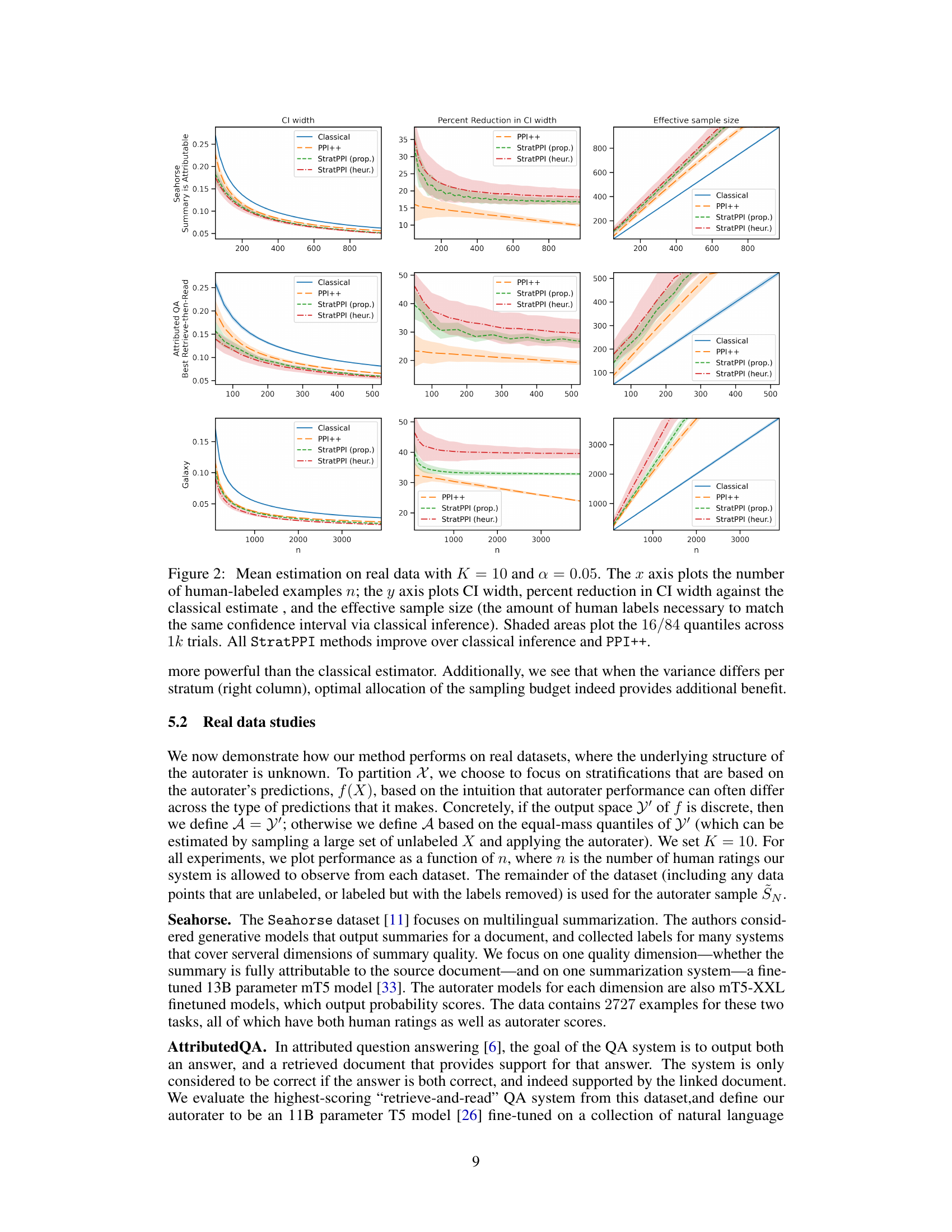
🔼 This figure shows the results of applying different methods (Classical, PPI++, StratPPI (proportional allocation), and StratPPI (heuristic allocation)) for mean estimation on real datasets. The x-axis represents the number of human-labeled examples (n), and the y-axis shows the confidence interval (CI) width, the percentage reduction in CI width compared to the classical method, and the effective sample size needed to achieve the same CI width with the classical method. The shaded areas represent the 16th and 84th percentiles across 1000 trials. The results demonstrate that stratified prediction-powered inference (StratPPI) consistently outperforms the classical and unstratified PPI++ methods by significantly reducing CI width and effective sample size.
read the caption
Figure 3: Mean estimation on real data with K = 10 and α = 0.05. The x axis plots the number of human-labeled examples n; the y axis plots CI width, percent reduction in CI width against the classical estimate, and the effective sample size (the amount of human labels necessary to match the same confidence interval via classical inference). Shaded areas plot the 16/84 quantiles across 1k trials. All StratPPI methods improve over classical inference and PPI++.
Full paper#