TL;DR#
Pearson’s r, a widely used correlation coefficient, is traditionally limited to measuring linear relationships. This limitation restricts its use in analyzing nonlinear data where relationships may still be monotone (i.e. consistently increasing or decreasing). Existing alternative methods for capturing nonlinear dependence often employ fundamentally different approaches than Pearson’s r, leaving an open question of how to effectively extend Pearson’s r to this wider class of relationships.
This paper proposes a refined version of Pearson’s r called ‘Rearrangement Correlation’, which overcomes the limitations of the original method. By using a sharper bound for covariance and focusing on monotone dependence, this new metric accurately measures both linear and nonlinear monotone relationships, outperforming existing methods in various experiments and demonstrating enhanced accuracy and robustness. This advancement provides a powerful tool for more precise analysis in numerous fields of study.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with correlation and dependence measures. It challenges the traditional limitations of Pearson’s r, presenting a novel approach to accurately capture nonlinear monotone relationships. This opens up new avenues for data analysis and provides a more accurate tool for various fields, directly impacting the reliability of statistical analyses and broadening their applications.
Visual Insights#

🔼 This figure illustrates the relationships among different correlation coefficients and their capture ranges based on covariance inequality series. It visually demonstrates how different scaling bounds affect the range of values each coefficient can capture and highlights the advantages of the proposed Rearrangement Correlation (r#), which expands the capture range beyond linear relationships to include arbitrary monotone relationships. The figure also shows that the Rearrangement Correlation reverts to Pearson’s r in the case of linear dependence.
read the caption
Figure 1: Covariance inequality series, correlation coefficients and their capture ranges
In-depth insights#
Pearson’s r Redefined#
The concept of “Pearson’s r Redefined” suggests a significant re-evaluation of this widely used correlation coefficient. Traditionally limited to assessing linear relationships, the core idea revolves around extending its applicability to capture arbitrary monotone dependencies. This involves a nuanced approach, moving beyond the typical scaling used in Pearson’s r by leveraging sharper mathematical bounds, leading to a refined measure denoted as r#. The key is to improve upon the classic Cauchy-Schwarz inequality to achieve tighter bounds, which unexpectedly broadens the measure’s capture range. This adjusted coefficient (r#) retains the simplicity of Pearson’s r while enhancing its accuracy in measuring nonlinear monotonic relationships. The implications are substantial for various fields reliant on correlation analysis, potentially offering more precise insights into relationships that are not strictly linear.
Monotone Dependence#
Monotone dependence, in the context of the provided research paper, signifies a relationship between two variables where an increase in one variable consistently leads to either an increase or a decrease in the other. This contrasts with more general forms of dependence where the relationship might be more complex or non-directional. The paper’s focus is on how Pearson’s correlation coefficient, traditionally associated with linear relationships, can be adapted to measure monotone dependence effectively. This adaptation centers on refining the coefficient’s bounds using sharper inequalities than the Cauchy-Schwarz Inequality, resulting in a new coefficient with enhanced accuracy. The core idea is that stricter bounds unexpectedly improve the coefficient’s ability to capture monotone relations. The research highlights the importance of considering the inherent limitations of standard correlation methods for non-linear scenarios and explores ways to address them through mathematical refinement and novel applications of established statistical tools.
Rearrangement Correlation#
The proposed “Rearrangement Correlation” offers a novel approach to measuring monotone dependence by refining Pearson’s r. It leverages a tighter inequality than the Cauchy-Schwarz inequality, expanding the coefficient’s capture range beyond linear relationships to encompass arbitrary monotone relationships, both linear and nonlinear. This is achieved by scaling the covariance using the absolute value of a rearranged covariance, instead of the standard deviation product. This adjustment doesn’t alter the coefficient’s boundedness (-1 to +1), but it significantly improves its accuracy in capturing nonlinear monotone dependence, as demonstrated through simulations and real-world data. A key advantage is that the new correlation reverts to Pearson’s r in linear scenarios, providing a unified approach for measuring both linear and nonlinear monotone relationships. The method, however, exhibits limitations in handling non-monotone dependencies, underscoring the need for specialized techniques in those scenarios.
Tighter Bounds#
The concept of “tighter bounds” in the context of correlation coefficients is crucial for improving the accuracy and effectiveness of dependence measures. Traditional methods often rely on loose bounds, such as the Cauchy-Schwarz inequality, which limit the range of correlation values and can obscure subtle relationships. By deriving tighter inequalities, researchers can create correlation coefficients with broader capture ranges that are more sensitive to various forms of dependence. The use of tighter bounds is particularly relevant when dealing with nonlinear monotone relationships, which are often missed by traditional linear correlation measures. This refinement of dependence measures allows for more accurate representation of complex associations between variables and is a significant development towards a more comprehensive understanding of statistical dependencies.
Simulation Study#
A robust simulation study is crucial for validating the proposed rearrangement correlation coefficient. It should involve generating data from a wide range of scenarios, including both simple and complex monotone relationships, to assess the method’s accuracy and robustness. Key aspects to consider are the variety of functional forms used to model the relationships, the inclusion of noise to simulate real-world conditions, and the range of dependence strengths (from weak to strong). Furthermore, comparing the rearrangement correlation’s performance against existing methods, like Spearman’s rho and Kendall’s tau, under these diverse conditions is vital. The study must also address potential limitations, such as sensitivity to outliers or computational efficiency, and provide a clear quantitative evaluation of the method’s performance using appropriate metrics, such as mean absolute error (MAE) or root mean squared error (RMSE). Visualizations, such as scatter plots and boxplots, should also be included to illustrate the results and facilitate understanding. The comprehensive nature and rigorous evaluation within the simulation study will significantly strengthen the paper’s credibility and contribute to a deeper understanding of the proposed method’s capabilities and limitations.
More visual insights#
More on figures

🔼 This figure illustrates the relationships between different correlation coefficients and their respective capture ranges. It shows how the choice of scaling bounds for the covariance (denominator in the correlation formula) affects the range of values the coefficient can capture. The figure demonstrates that looser bounds lead to narrower capture ranges (only capturing linear or additive relationships, or identical relationships), while tighter bounds expand the range (to include nonlinear monotone relationships). The figure highlights the relationships between the classic Cauchy-Schwarz inequality, looser bounds used in other correlation coefficients (such as r+ and r=), and the new, tighter bound introduced in the paper which is used to define the Rearrangement Correlation (r#).
read the caption
Figure 1: Covariance inequality series, correlation coefficients and their capture ranges
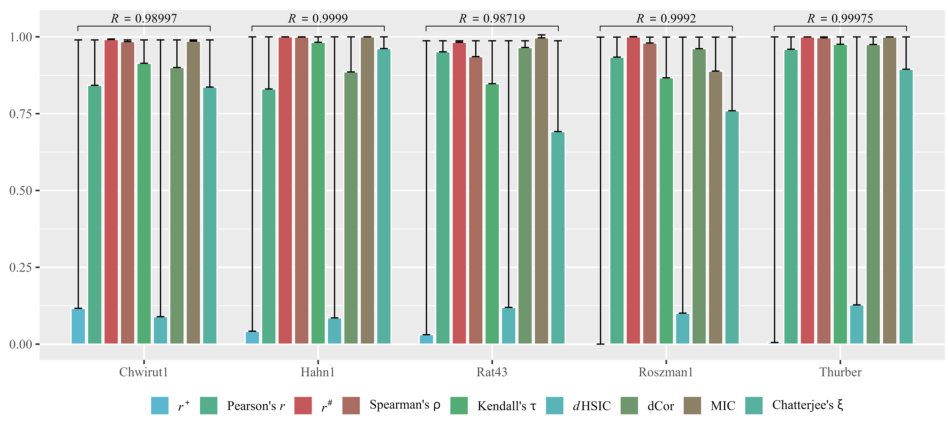
🔼 This figure compares the performance of nine different dependence measures (Pearson’s r, Spearman’s ρ, Kendall’s τ, dHSIC, dCor, MIC, Chatterjee’s ξ, r+, and r#) across five real-life datasets. For each dataset, the measures’ values are plotted as bars, with error bars representing the variability. The true dependence strength (R), verified by NIST, is indicated above each dataset. The figure visually demonstrates the accuracy of each measure in capturing the true dependence strength in real-world scenarios, highlighting the relative strengths and weaknesses of each approach.
read the caption
Figure 3: Performance of Different Measures in 5 Real-life Scenarios
Full paper#