TL;DR#
Autoformalization, translating natural language descriptions into formal language, is challenging. Existing Large Language Models (LLMs) show promising results but have a considerable gap between the top-1 and top-k accuracy. This means LLMs often require multiple tries before producing a correct formalization. This is inefficient and hinders real-world applications.
This research introduces a new self-consistent framework to address this issue. It ranks multiple LLM-generated formalizations by employing ‘symbolic equivalence’ (checking logical consistency) and ‘semantic consistency’ (measuring the similarity between the original and re-translated text). Extensive experiments demonstrate significant accuracy improvements across multiple LLMs and datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in AI and formal mathematics due to its novel approach to autoformalization, significantly improving accuracy and efficiency. It addresses limitations of existing methods, proposes a synergistic framework combining symbolic equivalence and semantic consistency checks. The work highlights the potential of enhanced LLMs for solving complex mathematical problems and opens new avenues for further research in automated reasoning and bridging the gap between natural and formal languages.
Visual Insights#

🔼 The figure shows an example of how GPT-4 translates a natural language mathematical statement into a formal Isabelle language version. The prompt is to formalize the statement ‘Find the product of 0.666… and 6. The answer is 4.’ GPT-4 generates four different Isabelle code versions as possible translations. Only two of these correctly represent the mathematical statement, showing the inherent challenge of accurately translating natural language into formal mathematical language, highlighting the unreliability of the grounding step (converting recurring decimals to their fractional equivalents).
read the caption
Figure 1: An illustrative example of autoformalization. The mathematical statement from the MATH dataset is translated into a formal version by GPT-4. Only two formalization results (No.2 and No.3) are correct, while the others fail in the grounding (0.\overline6 → 2/3).
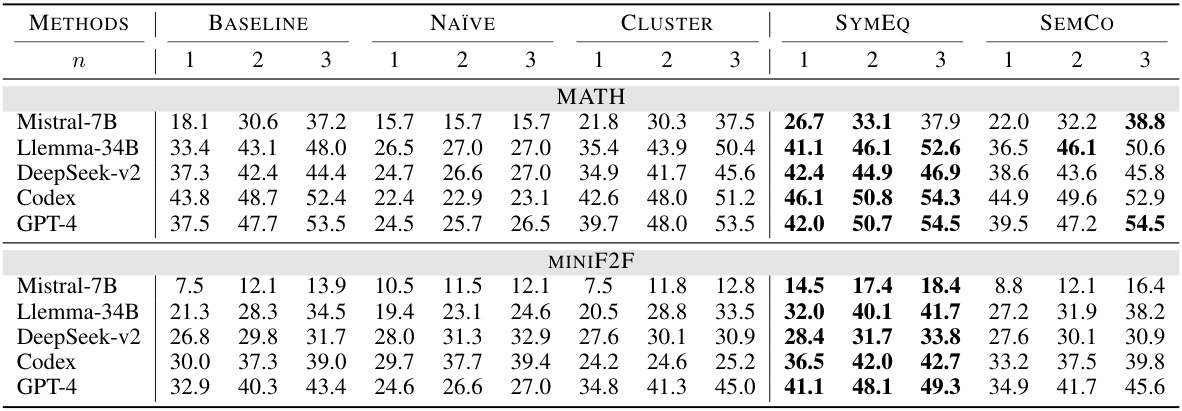
🔼 This table presents the performance comparison of different methods for autoformalizing mathematical statements, specifically focusing on the n@k accuracy metric where n represents the number of correct formalizations among the top k generated candidates. The methods compared include the proposed methods (SymEq and SemCo), a baseline method, a naive approach, a clustering technique, and are evaluated on two datasets, MATH and miniF2F. The best performance for each n (number of correct answers among the top k generations) is highlighted in bold, demonstrating the superior performance of the proposed methods.
read the caption
Table 1: Performance (n@k) of our methods (SymEq and SemCo) and comparison methods (Baseline, Naïve, and Cluster) on MATH and miniF2F datasets. The best performance of each n is in bold. The results show that our proposed methods consistently achieves superior performance.
In-depth insights#
LLM Autoformalization#
LLM autoformalization represents a significant advancement in automated reasoning, leveraging the power of large language models (LLMs) to translate natural language mathematical expressions into formal, machine-verifiable representations. This process is crucial for bridging the gap between human-readable mathematical descriptions and the formal systems required for automated theorem proving and verification. A key challenge highlighted is the discrepancy between the accuracy of top-1 (pass@1) and top-k (pass@k) LLM generated formalizations. This suggests inherent limitations in the ability of LLMs to consistently produce correct formalizations in a single attempt. To address this, the paper proposes a novel framework that incorporates methods for evaluating the self-consistency of LLM outputs through symbolic equivalence (using automated theorem provers) and semantic consistency (measuring the similarity between the original and re-informalized text embeddings). This dual approach aims to identify and select the most reliable formalization from multiple LLM candidates, significantly improving overall accuracy.
Dual Consistency#
The concept of “Dual Consistency” in a research paper likely refers to a methodology that leverages two complementary approaches to improve the robustness and accuracy of a system. This dual approach often involves combining a more symbolic, rule-based method with a semantic, meaning-based method. For instance, in natural language processing, one might combine a syntactic parser (symbolic) with a semantic role labeler (semantic). The dual consistency strategy would then evaluate the results from both methods, potentially using a weighted score or some other type of reconciliation to produce a final output. This dual approach offers resilience against errors inherent in either individual method and can significantly improve overall performance by combining their respective strengths. The effectiveness of this approach depends heavily on the specific problem being addressed and the choice of complementary methods. A well-designed dual consistency model would ideally highlight situations where the two methods disagree, prompting further investigation or refinement of the results. Careful consideration of the weighting and the interaction between the two methods are crucial for achieving the desired level of consistency and accuracy.
MATH & miniF2F#
The datasets MATH and miniF2F are crucial for evaluating the effectiveness of autoformalization techniques. MATH, a more general dataset, contains diverse high school level math problems, testing the robustness of models across various problem types. In contrast, miniF2F focuses on more challenging problems from Olympiads. Using both datasets allows for a thorough assessment of model capabilities, identifying strengths and weaknesses: a model might perform well on MATH but falter on the more complex miniF2F, highlighting potential limitations in handling advanced mathematical reasoning or specific problem structures. The combination provides a more comprehensive benchmark, allowing researchers to evaluate the generalizability and scalability of their approaches to varying problem difficulty and mathematical concepts. The results across these two datasets reveal critical information about the performance gap between simple and complex problem solving in autoformalization.
Synergy & Efficiency#
The study investigates the synergistic relationship between two novel self-consistency methods: symbolic equivalence and semantic consistency, for enhancing the accuracy of mathematical statement autoformalization. The results reveal a significant improvement when combining both methods compared to using either individually. This synergy highlights that verifying logical equivalence (symbolic equivalence) and preserving original meaning (semantic consistency) are complementary approaches, effectively addressing inconsistencies across different autoformalization candidates. Furthermore, the combined approach demonstrates notable efficiency gains by minimizing the need for manual intervention in correcting and validating formalization outputs, thus reducing the overall effort in the autoformalization process. The study’s focus on both synergy and efficiency underscores its practicality and potential for wider application in automated reasoning tasks.
Future Directions#
The research paper’s ‘Future Directions’ section would ideally delve into expanding the framework’s capabilities. Extending support for additional theorem provers like Lean 4 would enhance verification breadth. Integrating more advanced or fine-tuned LLMs such as those specializing in mathematical reasoning could significantly improve accuracy and efficiency. A key area for advancement is generating higher-quality, aligned datasets of informal and formal mathematical statements. This would involve methods for automatically creating such pairs or leveraging existing resources more effectively. Finally, exploring the integration of external knowledge bases to resolve ambiguities and fill knowledge gaps within the LLMs would be beneficial. Addressing these areas will move the field closer to a robust and practical autoformalization system.
More visual insights#
More on figures
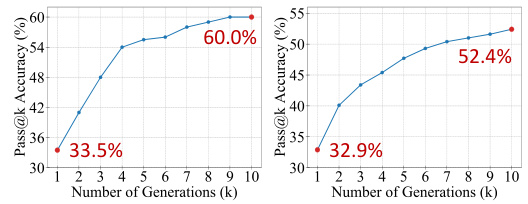
🔼 This figure displays two graphs illustrating the pass@k accuracy for GPT-4 on the MATH and miniF2F datasets. The x-axis represents the number of generations (k), and the y-axis shows the pass@k accuracy. The left graph shows MATH dataset results, and the right graph shows miniF2F dataset results. Both graphs show a clear upward trend in accuracy as the number of generations increases, but the rate of improvement slows significantly after around k=10.
read the caption
Figure 2: Pass@k curves for GPT-4 autoformalization on the MATH (left) and miniF2F (right) datasets. The results show that LLMs can achieve higher coverage of correct formal statements with an increasing number of generated candidates up to k = 10. Beyond this point, the improvement gradually diminishes as k continues to increase.
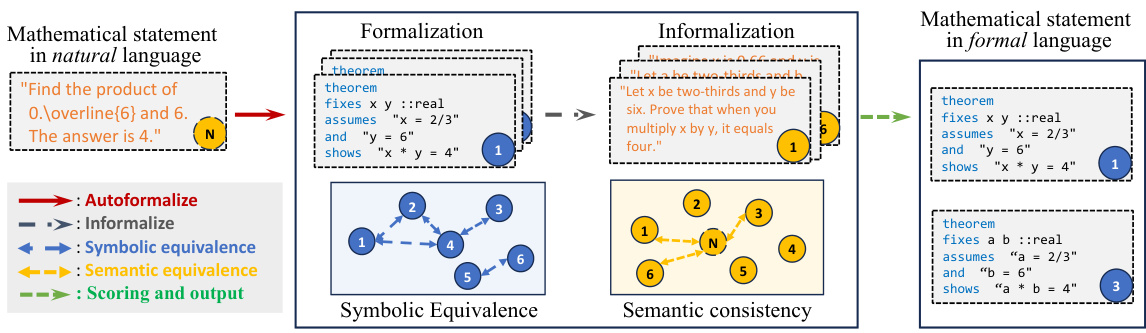
🔼 This figure illustrates the workflow of the proposed autoformalization framework. It starts with a mathematical statement in natural language. The framework then uses LLMs to generate multiple formalization candidates in a formal language. Symbolic equivalence compares these candidates to identify logically equivalent ones, and semantic consistency measures the similarity between re-informalized candidates and the original statement using embeddings. Finally, scores from both methods are combined to select the best formalization result.
read the caption
Figure 3: The overview of our autoformalization framework. In the framework, symbolic equivalence is constructed among formalized statements, and semantic consistency is computed between the informalized statements and the original statement. The scores from these two evaluations are combined to rank and select the final formalization results.
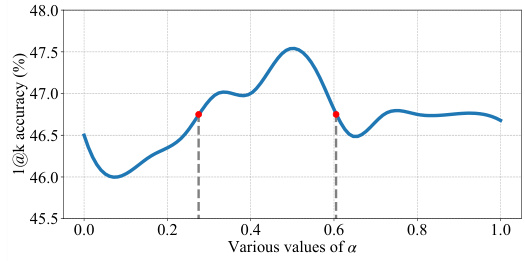
🔼 This figure shows the performance of the log-combination strategy for various values of α (alpha), a hyperparameter controlling the trade-off between symbolic equivalence and semantic consistency. The x-axis represents different values of α, ranging from 0 to 1. The y-axis shows the 1@k accuracy (percentage of problems correctly formalized among the top k generated results), achieved by GPT-4. The curve demonstrates that a specific range of α values yields significantly higher 1@k accuracy than other values, suggesting a synergistic relationship between the two self-consistency methods. The optimal range of α for improved performance is highlighted.
read the caption
Figure 4: Performance curve of log-comb for different values of α. The formalization results are generated by GPT-4. The results show that the combination can further improve the autoformalization accuracy with a large sweet spot.
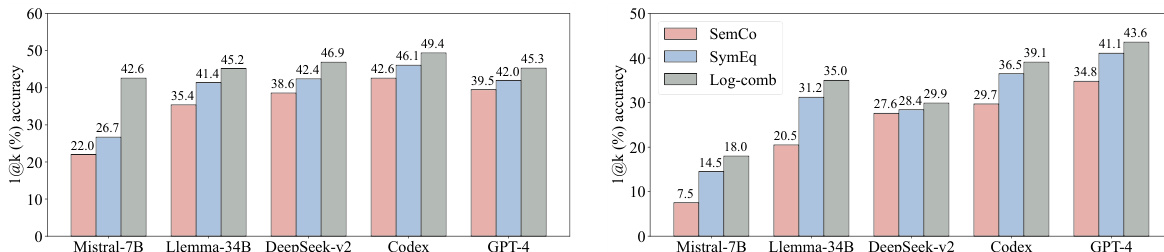
🔼 This figure displays the performance of the proposed log-comb combination strategy on two datasets, MATH and miniF2F. The results demonstrate that log-comb consistently improves the autoformalization accuracy for various LLMs. The left panel shows the results on the MATH dataset, while the right panel shows the results on the miniF2F dataset. The y-axis represents the 1@k accuracy, while the x-axis lists the LLMs. The bars for each LLM represent the performance of SemCo, SymEq, and log-comb respectively. The results highlight the synergistic effect of combining symbolic equivalence and semantic consistency to boost autoformalization performance.
read the caption
Figure 5: The performance of our proposed combination strategy (log-comb) on the MATH (left) and miniF2F (right) datasets. The results show that the log-comb further boost the autoformalization performance across various LLMs on the two datasets.
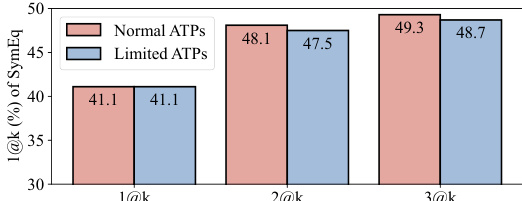
🔼 This figure shows the performance of the SymEq method (symbolic equivalence) using different ATP (Automated Theorem Prover) settings. The formalization results were generated using the GPT-4 language model. The key finding is that increasing the power of the ATP doesn’t significantly improve the performance of SymEq, suggesting that the limitations of the approach lie elsewhere, and not solely in the capabilities of the theorem prover.
read the caption
Figure 6: Performance of SymEq using different ATP settings, with formalization results generated by GPT-4. The results indicate that the performance improvement is very narrow by increasing the capability of ATPs.
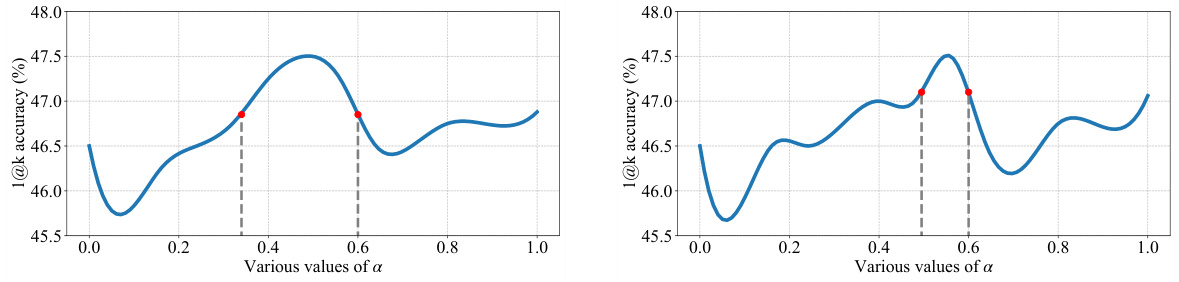
🔼 This figure displays the performance curves for linear and quadratic combination strategies, varying the hyperparameter α (alpha) from 0 to 1. The curves represent the 1@k accuracy (the proportion of tasks where at least one of the top-k generated formalizations is correct) achieved by each combination method when applied to GPT-4’s autoformalization results. The figure highlights that both methods generally improve accuracy but that the quadratic method has a narrower range of effective alpha values compared to the linear method.
read the caption
Figure 7: Performance curves of linear- (left) and quad- (right) comb across various values of α. The formalization results are generated by GPT-4. The results show that both combination strategies successfully improve autoformalization accuracy, while the effective range of quad-comb is smaller.
More on tables
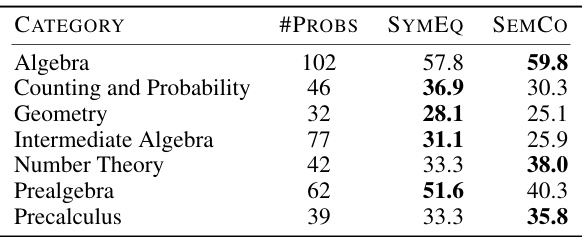
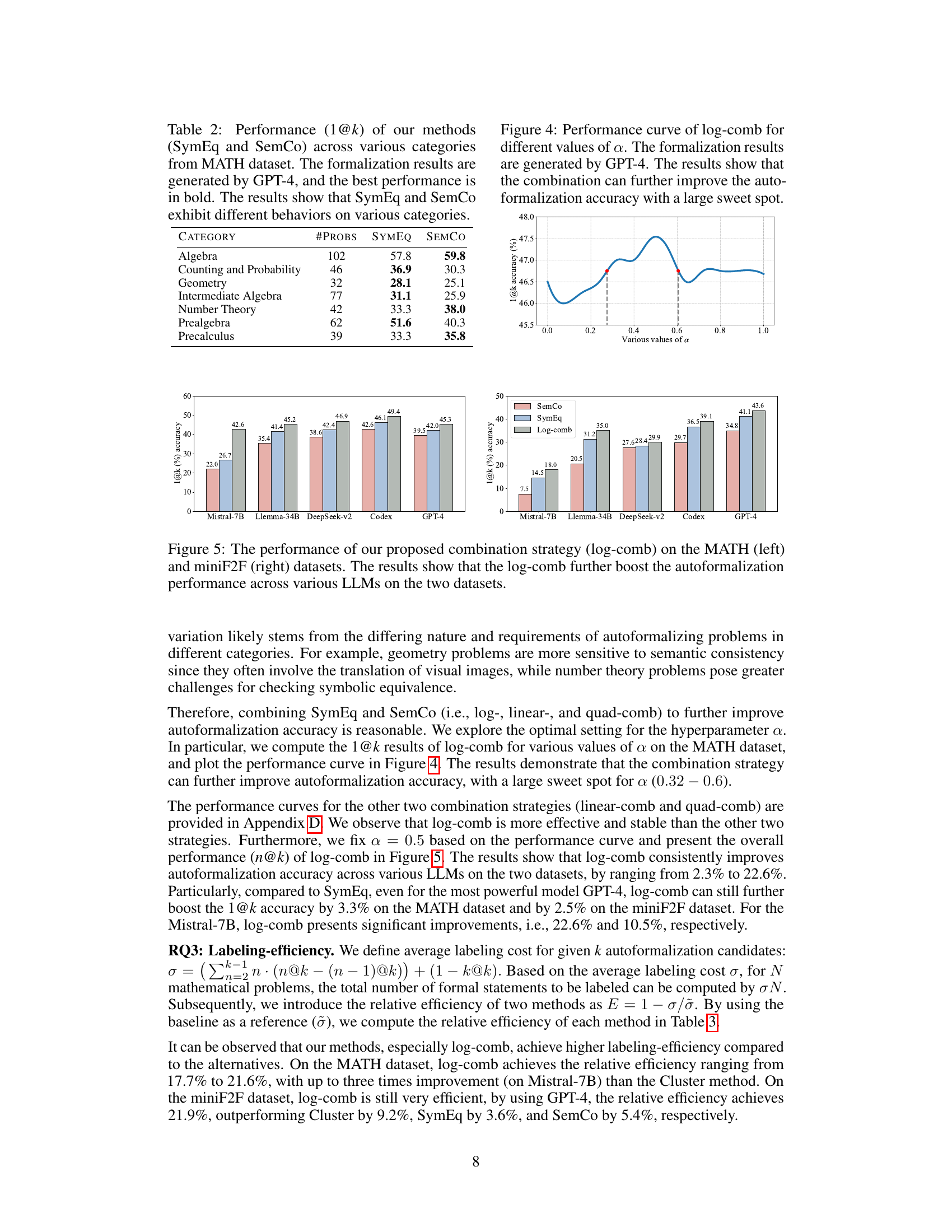
🔼 This table shows the performance of the Symbolic Equivalence (SymEq) and Semantic Consistency (SemCo) methods across different categories of the MATH dataset. The results are specifically for GPT-4 and highlight the varying effectiveness of each method depending on problem type (e.g., Algebra, Geometry, Number Theory). The best performance in each category is highlighted in bold.
read the caption
Table 2: Performance (1@k) of our methods (SymEq and SemCo) across various categories from MATH dataset. The formalization results are generated by GPT-4, and the best performance is in bold. The results show that SymEq and SemCo exhibit different behaviors on various categories.

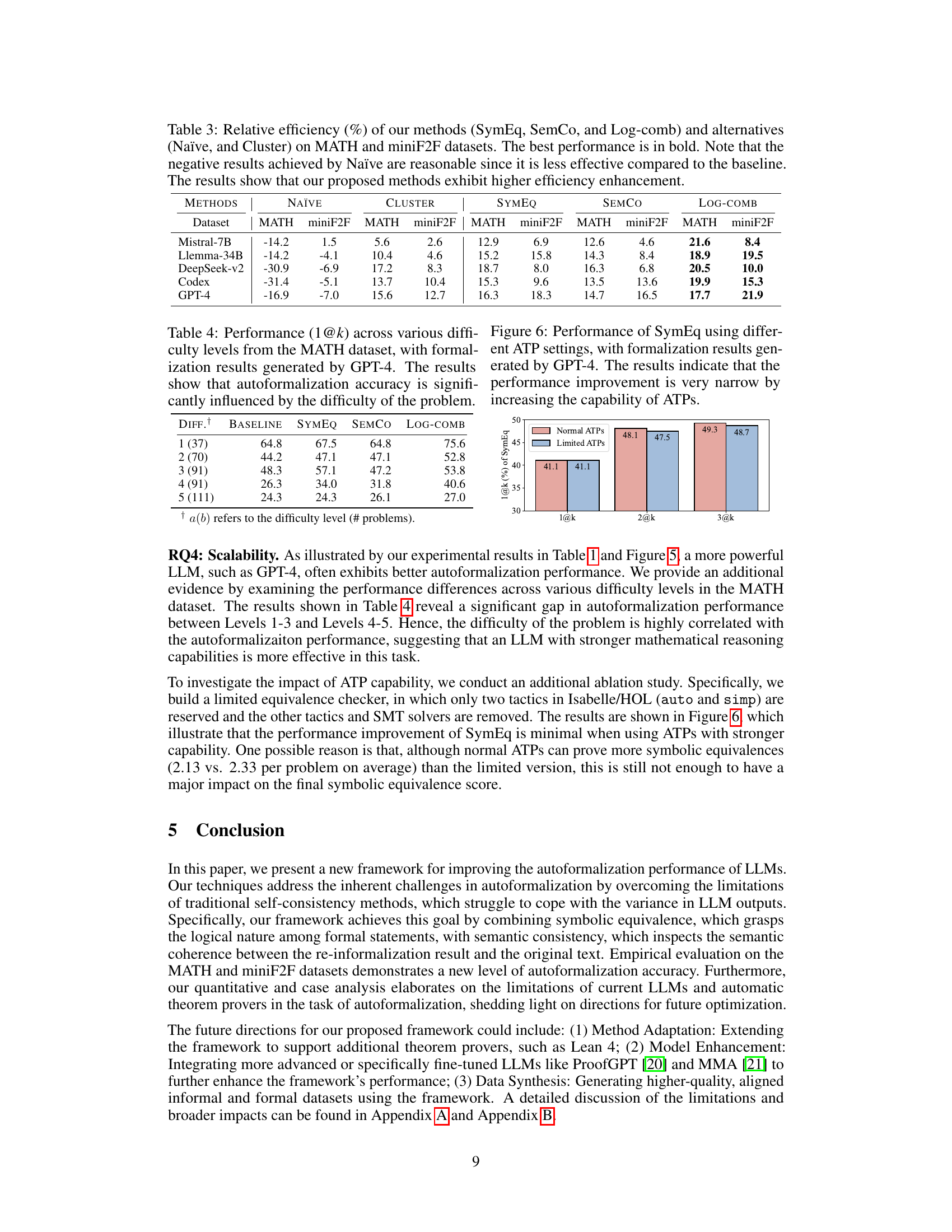
🔼 This table presents the relative efficiency of different methods for autoformalization, comparing the proposed methods (SymEq, SemCo, Log-comb) against baseline and alternative approaches (Naïve, Cluster). Relative efficiency is calculated based on the reduction in manual labeling effort. The table shows that the proposed methods significantly improve efficiency compared to the baselines, with Log-comb consistently achieving the best performance.
read the caption
Table 3: Relative efficiency (%) of our methods (SymEq, SemCo, and Log-comb) and alternatives (Naïve, and Cluster) on MATH and miniF2F datasets. The best performance is in bold. Note that the negative results achieved by Naïve are reasonable since it is less effective compared to the baseline. The results show that our proposed methods exhibit higher efficiency enhancement.
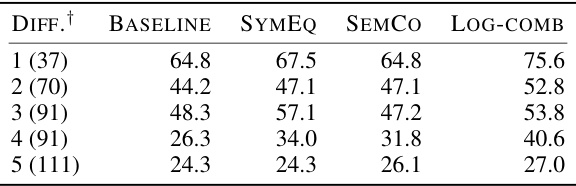
🔼 This table presents the performance (1@k accuracy) of the GPT-4 model on the MATH dataset, categorized by difficulty levels. It demonstrates how the autoformalization accuracy varies across different difficulty levels, highlighting the impact of problem complexity on the model’s performance.
read the caption
Table 4: Performance (1@k) across various difficulty levels from the MATH dataset, with formalization results generated by GPT-4. The results show that autoformalization accuracy is significantly influenced by the difficulty of the problem.
Full paper#